Eigen Decomposition and Singular Value Decomposition Based on

Eigen Decomposition and Singular Value Decomposition Based on the slides by Mani Thomas Modified and extended by Longin Jan Latecki

Introduction n Eigenvalue decomposition q n n n Physical interpretation of eigenvalue/eigenvectors Singular Value Decomposition Importance of SVD q q q n Spectral decomposition theorem Matrix inversion Solution to linear system of equations Solution to a homogeneous system of equations SVD application

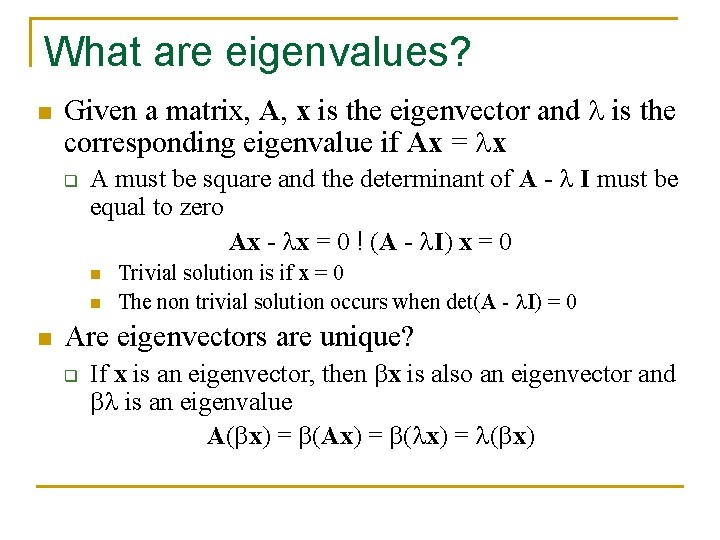
What are eigenvalues? n Given a matrix, A, x is the eigenvector and is the corresponding eigenvalue if Ax = x q A must be square and the determinant of A - I must be equal to zero Ax - x = 0 ! (A - I) x = 0 n n n Trivial solution is if x = 0 The non trivial solution occurs when det(A - I) = 0 Are eigenvectors are unique? q If x is an eigenvector, then x is also an eigenvector and is an eigenvalue A( x) = (Ax) = ( x)

Calculating the Eigenvectors/values Expand the det(A - I) = 0 for a 2 £ 2 matrix n n For a 2 £ 2 matrix, this is a simple quadratic equation with two solutions (maybe complex) n This “characteristic equation” can be used to solve for x

Eigenvalue example n Consider, n The corresponding eigenvectors can be computed as q q For = 0, one possible solution is x = (2, -1) For = 5, one possible solution is x = (1, 2) For more information: Demos in Linear algebra by G. Strang, http: //web. mit. edu/18. 06/www/

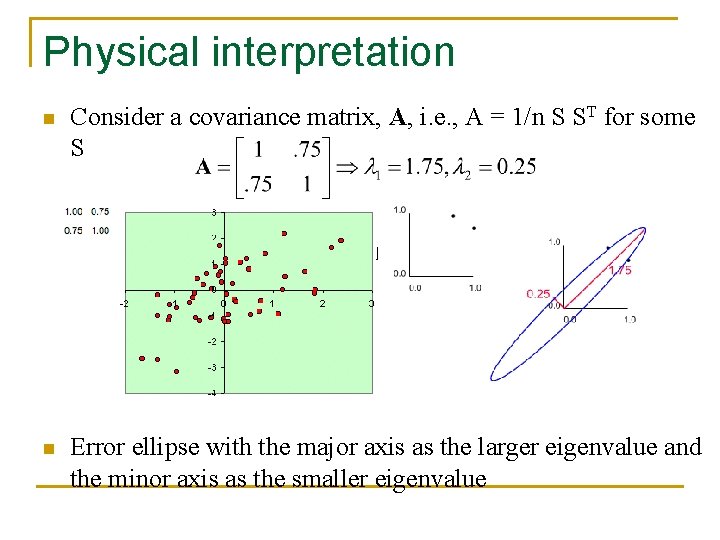
Physical interpretation n Consider a covariance matrix, A, i. e. , A = 1/n S ST for some S n Error ellipse with the major axis as the larger eigenvalue and the minor axis as the smaller eigenvalue

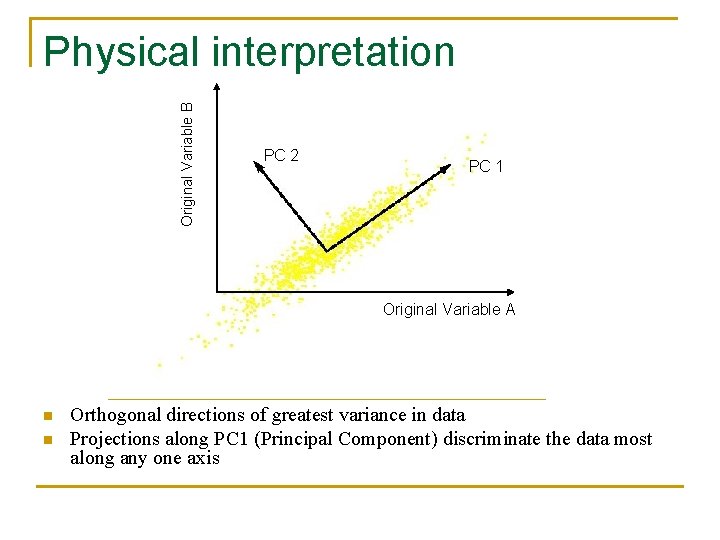
Original Variable B Physical interpretation PC 2 PC 1 Original Variable A n n Orthogonal directions of greatest variance in data Projections along PC 1 (Principal Component) discriminate the data most along any one axis

Physical interpretation n n First principal component is the direction of greatest variability (covariance) in the data Second is the next orthogonal (uncorrelated) direction of greatest variability q n n So first remove all the variability along the first component, and then find the next direction of greatest variability And so on … Thus each eigenvectors provides the directions of data variances in decreasing order of eigenvalues For more information: See Gram-Schmidt Orthogonalization in G. Strang’s lectures

Multivariate Gaussian

Bivariate Gaussian

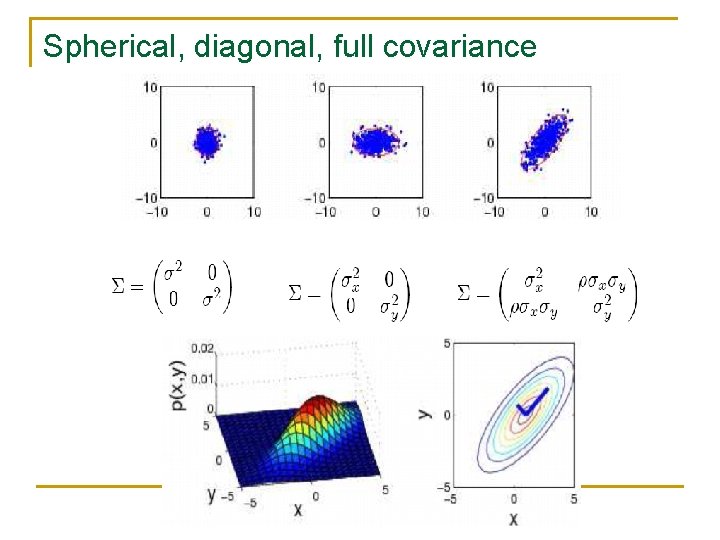
Spherical, diagonal, full covariance

Eigen/diagonal Decomposition n n Let be a square matrix with m linearly independent eigenvectors (a “non-defective” matrix) Unique Theorem: Exists an eigen decomposition diagonal q (cf. matrix diagonalization theorem) n Columns of U are eigenvectors of S n Diagonal elements of are eigenvalues of for distinct eigenvalues

Diagonal decomposition: why/how Let U have the eigenvectors as columns: Then, SU can be written Thus SU=U , or U– 1 SU= And S=U U– 1.

Diagonal decomposition example Recall The eigenvectors Inverting, we have Then, S=U U– 1 = and form Recall UU– 1 =1.

Example continued Let’s divide U (and multiply U– 1) by Then, S= Q Why? Stay tuned … (Q-1= QT )

Symmetric Eigen Decomposition n If n Theorem: Exists a (unique) eigen decomposition n is a symmetric matrix: where Q is orthogonal: q Q-1= QT q Columns of Q are normalized eigenvectors q Columns are orthogonal. q (everything is real)

Spectral Decomposition theorem n If A is a symmetric and positive definite k £ k matrix (x. TAx > 0) with i ( i > 0) and ei, i = 1 k being the k eigenvector and eigenvalue pairs, then q n This is also called the eigen decomposition theorem Any symmetric matrix can be reconstructed using its eigenvalues and eigenvectors

Example for spectral decomposition n Let A be a symmetric, positive definite matrix n n The eigenvectors for the corresponding eigenvalues are Consequently,

Singular Value Decomposition n If A is a rectangular m £ k matrix of real numbers, then there exists an m £ m orthogonal matrix U and a k £ k orthogonal matrix V such that q is an m £ k matrix where the (i, j)th entry i ¸ 0, i = 1 min(m, k) and the other entries are zero n n The positive constants i are the singular values of A If A has rank r, then there exists r positive constants 1, 2, r, r orthogonal m £ 1 unit vectors u 1, u 2, , ur and r orthogonal k £ 1 unit vectors v 1, v 2, , vr such that q Similar to the spectral decomposition theorem

Singular Value Decomposition (contd. ) n If A is a symmetric and positive definite then q SVD = Eigen decomposition n EIG( i) = SVD( i 2) n Here AAT has an eigenvalue-eigenvector pair ( i 2, ui) n Alternatively, the vi are the eigenvectors of ATA with the same non zero eigenvalue i 2

Example for SVD n Let A be a symmetric, positive definite matrix q U can be computed as q V can be computed as

Example for SVD n n n Taking 21=12 and 22=10, the singular value decomposition of A is Thus the U, V and are computed by performing eigen decomposition of AAT and ATA Any matrix has a singular value decomposition but only symmetric, positive definite matrices have an eigen decomposition

Applications of SVD in Linear Algebra n Inverse of a n £ n square matrix, A If A is non-singular, then A-1 = (U VT)-1= V -1 UT where -1=diag(1/ 1, , 1/ n) q If A is singular, then A-1 = (U VT)-1¼ V 0 -1 UT where 0 -1=diag(1/ 1, 1/ 2, , 1/ i, 0, 0, , 0) q n Least squares solutions of a m£n system q q n Ax=b (A is m£n, m¸n) =(ATA)x=ATb ) x=(ATA)-1 ATb=A+b If ATA is singular, x=A+b¼ (V 0 -1 UT)b where 0 -1 = diag(1/ 1, 1/ 2, , 1/ i, 0, 0, , 0) Condition of a matrix q Condition number measures the degree of singularity of A n Larger the value of 1/ n, closer A is to being singular http: //www. cse. unr. edu/~bebis/Math. Methods/SVD/lecture. pdf

Applications of SVD in Linear Algebra n Homogeneous equations, Ax = 0 q q Minimum-norm solution is x=0 (trivial solution) Impose a constraint, “Constrained” optimization problem Special Case n q If rank(A)=n-1 (m ¸ n-1, n=0) then x= vn ( is a constant) Genera Case n If rank(A)=n-k (m ¸ n-k, nk+1= = n=0) then x= 1 vn 2 2 k+1+ + kvn with 1+ + n=1 n Has appeared before q q q Homogeneous solution of a linear system of equations Computation of Homogrpahy using DLT Estimation of Fundamental matrix For proof: Johnson and Wichern, “Applied Multivariate Statistical Analysis”, pg 79

What is the use of SVD? n n SVD can be used to compute optimal low-rank approximations of arbitrary matrices. Face recognition q n Data mining q n Represent the face images as eigenfaces and compute distance between the query face image in the principal component space Latent Semantic Indexing for document extraction Image compression q Karhunen Loeve (KL) transform performs the best image compression n In MPEG, Discrete Cosine Transform (DCT) has the closest approximation to the KL transform in PSNR

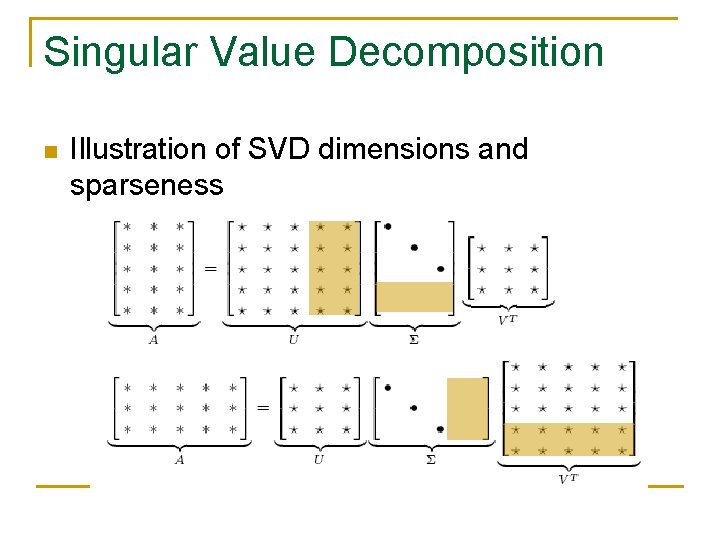
Singular Value Decomposition n Illustration of SVD dimensions and sparseness

SVD example Let Thus m=3, n=2. Its SVD is Typically, the singular values arranged in decreasing order.

Low-rank Approximation n n SVD can be used to compute optimal lowrank approximations. Approximation problem: Find Ak of rank k such that Frobenius norm Ak and X are both m n matrices. Typically, want k << r. n

Low-rank Approximation n Solution via SVD set smallest r-k singular values to zero k column notation: sum of rank 1 matrices

Approximation error n n How good (bad) is this approximation? It’s the best possible, measured by the Frobenius norm of the error: where the i are ordered such that i i+1. Suggests why Frobenius error drops as k increased.