EGR 1101 Unit 7 Systems of Linear Equations

EGR 1101 Unit 7 Systems of Linear Equations in Engineering (Chapter 7 of Rattan/Klingbeil text)

Systems of Linear Equations ¡ A linear equation in one variable has a unique solution. l ¡ A linear equation in two variables does not have a unique solution. l ¡ Example: 2 x=8 has a unique solution, namely x=4. Example: 3 x-4 y=7 does not have a unique solution. But a system of two independent linear equations in two variables does have a unique solution. l Example: The pair of equations 3 x-4 y=7 and 2 x+8 y=26 has a unique solution, namely x=5 and y=2.

Generalizing ¡ More generally, for any positive integer n, a system of n independent linear equations in n variables does have a unique solution. l It’s not unusual in engineering problems to end up with, say, eight equations in eight variables.

Four Methods ¡ We’ll study four methods for attacking such problems: 1. 2. 3. 4. ¡ Substitution Graphical method Matrix algebra Cramer’s Rule (a shortcut derived from matrix algebra) For a given problem, all four methods should give the same solution!

Today’s Examples 1. 2. Currents in a two-loop circuit Forces in static equilibrium: Hanging weight

A 2 -by-2 Matrix Equation ¡ ¡ Suppose we have the system of equations a 11 x 1 + a 12 x 2 = b 1 a 21 x 1 + a 22 x 2 = b 2 We can write this in matrix form as or Ax=b

Rewriting a Matrix Equation ¡ ¡ ¡ Suppose that in the matrix equation Ax=b A is a matrix of known constants, and x is a vector of unknowns, and b is a vector of known constants. We can solve for the unknowns in x by rewriting this equation as x = A-1 b The problem becomes: How do we find the inverse matrix A-1?

Determinant of a 2 -by-2 Matrix ¡ Suppose we have a matrix A given by ¡ This matrix’s determinant is given by |A| a 11 a 22 a 12 a 21 ¡ We sometimes use the symbol for the determinant.

Inverse of a 2 -by-2 Matrix ¡ Suppose again we have a matrix A given by ¡ This matrix’s inverse is given by

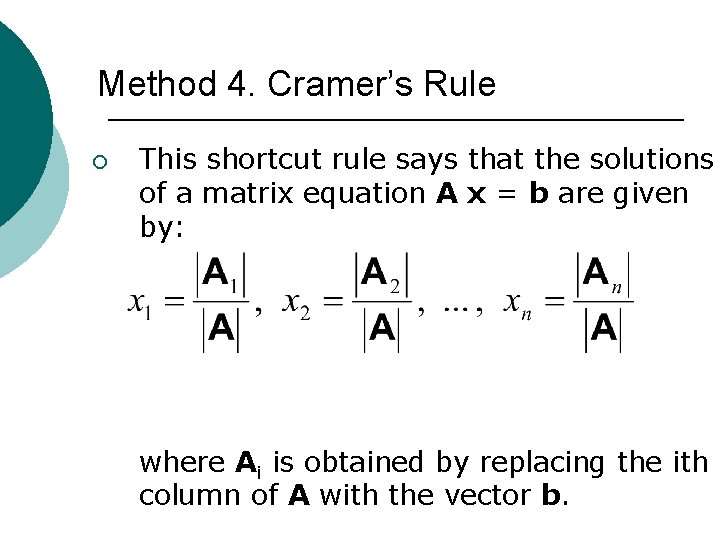
Method 4. Cramer’s Rule ¡ This shortcut rule says that the solutions of a matrix equation A x = b are given by: where Ai is obtained by replacing the ith column of A with the vector b.

Solving Matrix Equations with MATLAB ¡ ¡ First, define our coefficient matrix and our vector of constants: >> A = [10 4; 4 12] >> b = [6; 9] MATLAB offers at least three ways to proceed from here: >> x = inv(A)*b >> x = A^-1 * b >> x = A b