Efficient Steiner Tree Construction Based on Spanning Graphs

Efficient Steiner Tree Construction Based on Spanning Graphs Hai Zhou Electrical and Computer Engineering Northwestern University

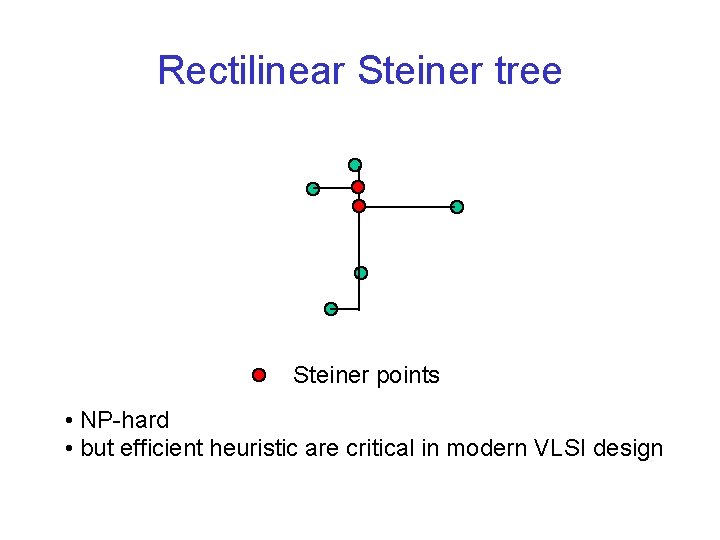
Rectilinear Steiner tree Steiner points • NP-hard • but efficient heuristic are critical in modern VLSI design

Spanning tree as a starting point • L(MST) <= 1. 5 L(SMT) • Shorten tree length by modification

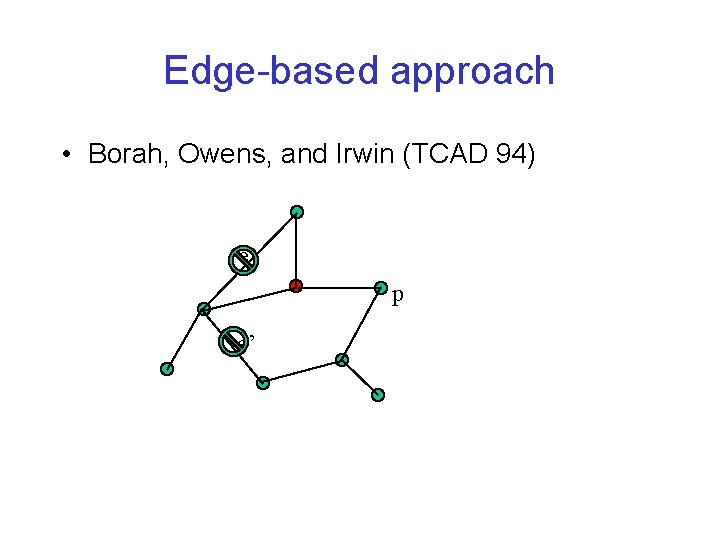
Edge-based approach • Borah, Owens, and Irwin (TCAD 94) e p e’

Questions • How to construct the initial spanning tree? • How to find the edge point pair candidates for connection? • How to find the longest edge on the formed cycle?

Answer: spanning graphs

Answer: spanning graphs • A graph on a set of given points • A MST on the graph is a MST of the given points – geometrical MST = spanning graph + graph MST • Spanning graph also represent geometrical proximity information – it also provides candidates for point-edge connection • It is a sparse graph: O(n) number of edges

Spanning graphs in O(n log n) time Euclidean Delaunay divide&conquer (Shamos 78? ) sweep-line (Fortune 87) rectilinear Delaunay Non-Delaunay div. &con. (Hwang 79) (Guibas et al 83) sweep-line (Shute et al 91) (Zhou et al 01)

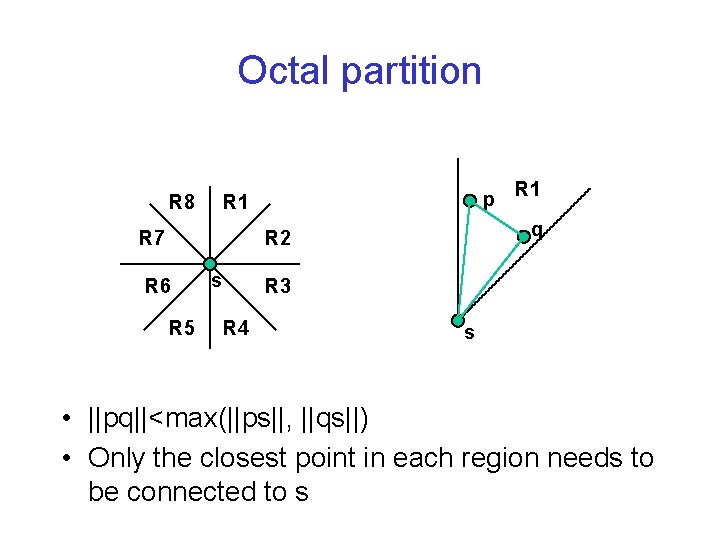
Octal partition R 8 p R 1 q R 1 R 7 R 2 R 6 R 5 s R 3 R 4 s • ||pq||<max(||ps||, ||qs||) • Only the closest point in each region needs to be connected to s

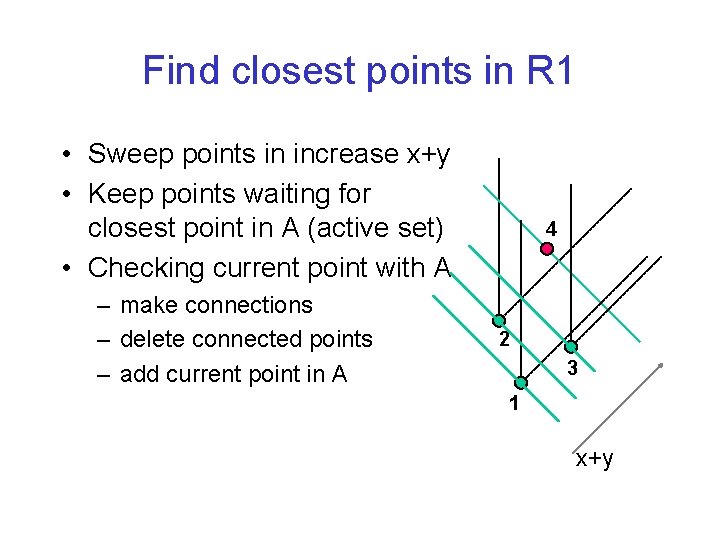
Find closest points in R 1 • Sweep points in increase x+y • Keep points waiting for closest point in A (active set) • Checking current point with A – make connections – delete connected points – add current point in A 4 2 3 1 x+y

Active set • Active set can be linearly order according to x • Use a binary search tree – Finding insertion place O(log n) – Deleting each point O(log n) – Inserting a point O(log n) • Each point is inserted and deleted at most once: O(n log n)

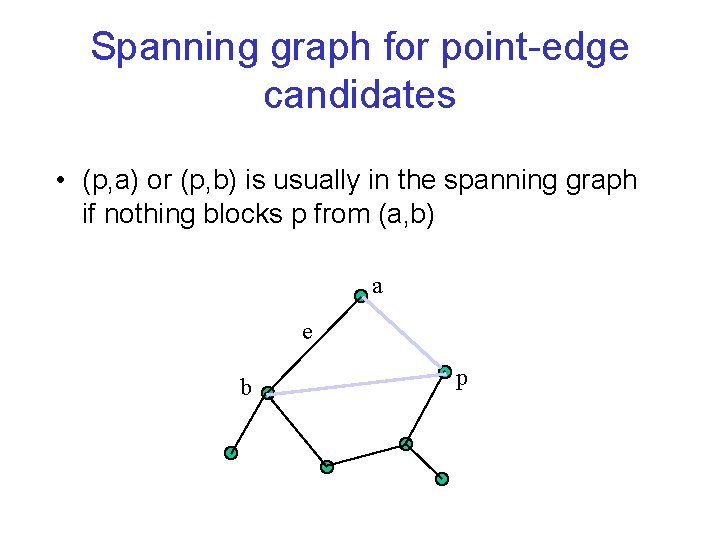
Spanning graph for point-edge candidates • (p, a) or (p, b) is usually in the spanning graph if nothing blocks p from (a, b) a e b p

Finding longest edge on cycle • Use Tarjan’s least common ancestor algorithm • Almost linear time • The bug appeared in Borah’s original O(n 2) algorithm does not exist here (proved)

Algorithm RST • construct a rectilinear spanning graph • sort the edges in the graph • use Kruskal to build MST, at the same time – build the merging binary tree and – possible point-edge candidates (by spanning graph) • use least common ancestors on merging binary tree to find the longest edges in cycles • iteratively update point-edge connections

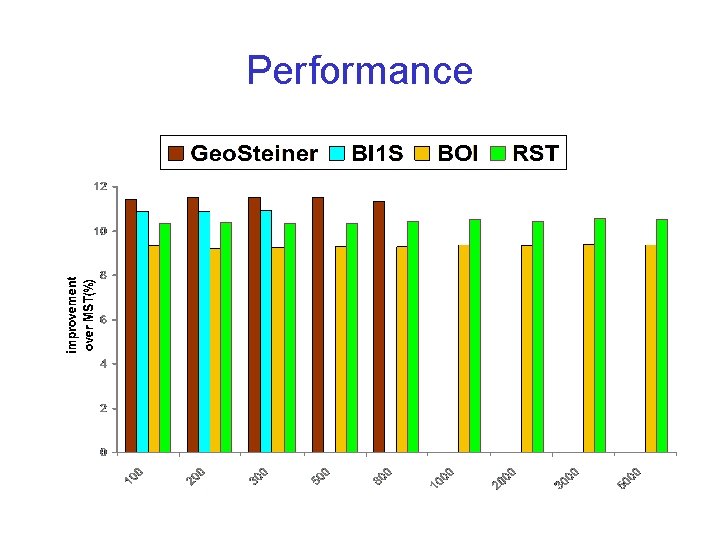
Performance

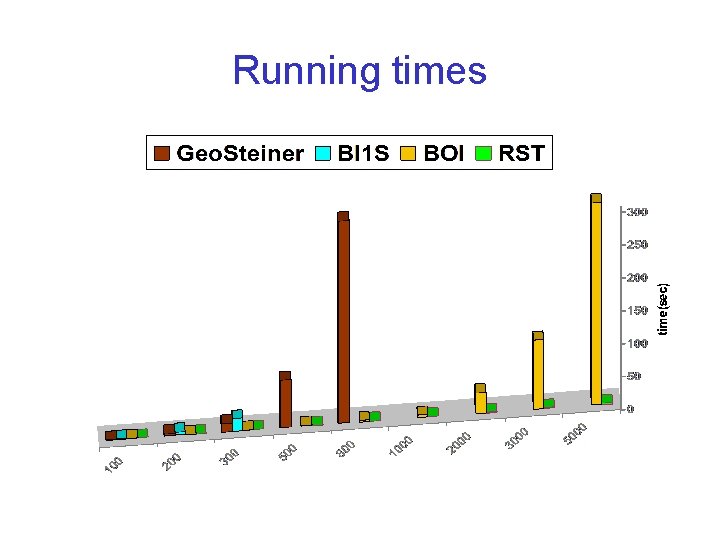
Running times

Correction • The running times of RST reported in the paper are much worse because we accidentally switched the sorting method to bubble sort (O(n 2)) instead of quick sort

BGA • Mandoiu et al. (ASP-DAC 03) • Similar to Borah et al. but more general • O(nlog 2 n) e e’

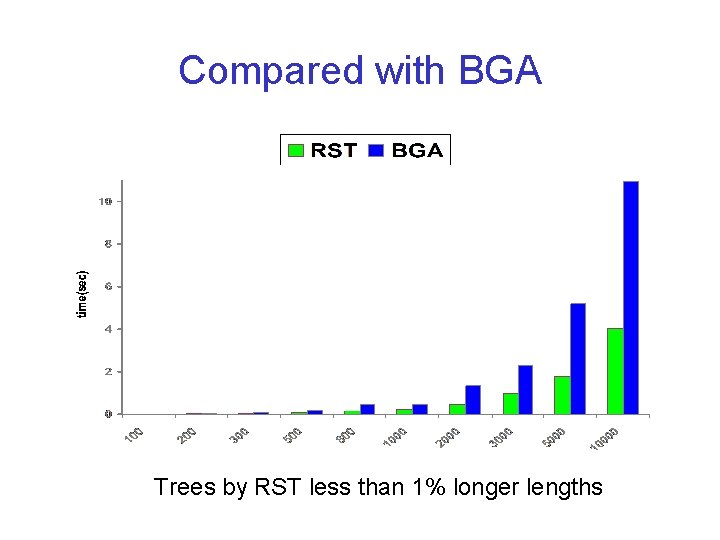
Compared with BGA Trees by RST less than 1% longer lengths

Summary • Besides generating spanning trees, spanning graphs also provide proximity information • Use for Steiner tree improvements • RST: efficient O(nlog n) heuristic • Future research: improving tree lengths