Efficient Reasoning on Finite Satisfiability in UML Class

Efficient Reasoning on Finite Satisfiability in UML Class Diagrams Azzam Maraee Victor Makarenkov Mira Balaban

Agenda • • Example Reasoning Problems Previous works Research Contribution • Conclusions and Future Work 2

Motivation [Protein] [Chemical] [Enzyme]=2* [catalyzed. Reaction] [Enzyme] [Protein] [Chemical] [Reaction] [catalyzed. Reaction] =1/2*[Enzyme] 2*[Chemical] ½*[Protein] ½* [Chemical]

Agenda • • Background Reasoning Problems Previous works Research Contribution – Finite Satisfiability Method: • Class Hierarchy and Generalization Set Constraints • Conclusions and Future Work 4

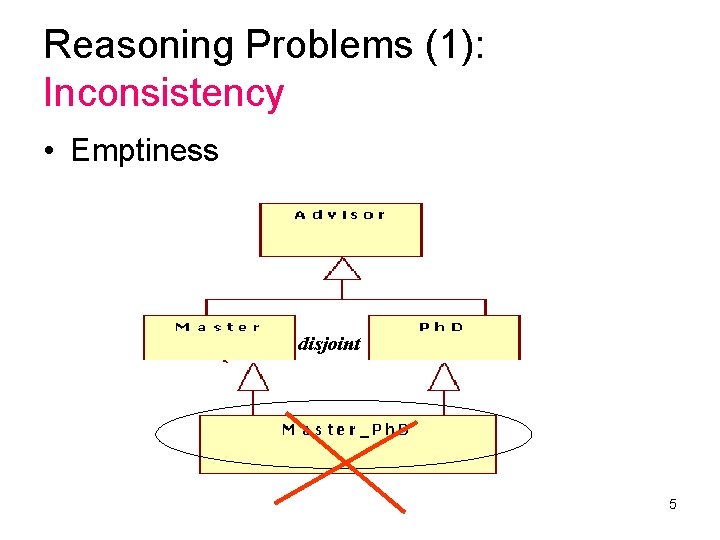
Reasoning Problems (1): Inconsistency • Emptiness disjoint 5

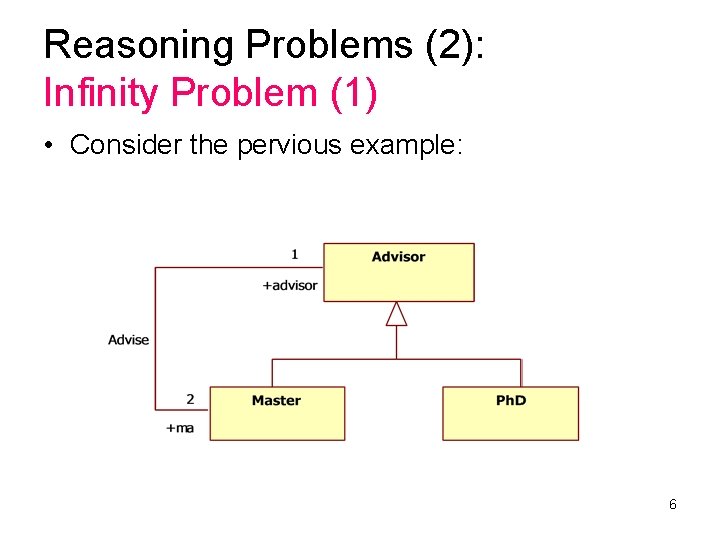
Reasoning Problems (2): Infinity Problem (1) • Consider the pervious example: 6

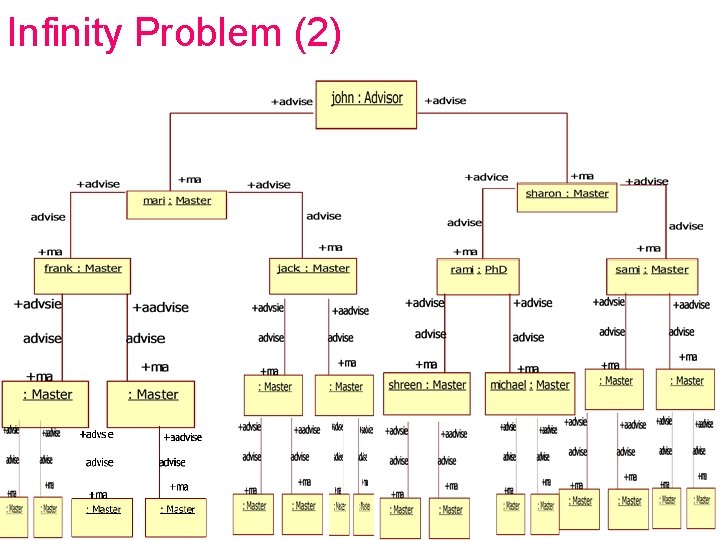
Infinity Problem (2) 7

Definitions • A legal instance of a class diagram is an instance that satisfies all constraints. • A class is consistent if it has a non empty extension in some legal instance. • A class is finitely satisfiable if it has a non empty extension in some legal instance. 8

Relevance of Reasoning • It is important to guarantee that models provide a reliable support for the designed systems. – Implementability : A class diagram is implemented into a running system. – Project cost: Early detection of problems. – Used with MDA: Precise and consistent enough to be used within MDA. 9

Reasoning Needs (2) • Current case tools do not support reasoning tasks. • Need for powerful CASE tools – with reasoning capabilities. 10

Agenda • • Background Reasoning Problems Previous works Research Contribution – Finite Satisfiability Method. • Class Hierarchy and Generalization Set Constraints • Conclusions and Future Work 11

Testing Finite Satisfiability • Lenzerini and Nobili (92): – ER diagrams without class hierarchy. • Calvanese and Lenzerini (94): – Extend with class hierarchy. 12

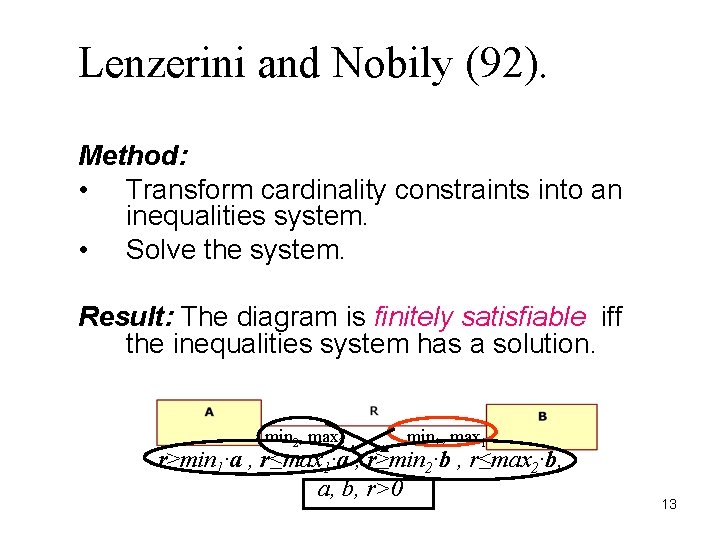
Lenzerini and Nobily (92). Method: • Transform cardinality constraints into an inequalities system. • Solve the system. Result: The diagram is finitely satisfiable iff the inequalities system has a solution. min 2, max 2 min 1, max 1 r≥min 1∙a , r≤max 1∙a , r≥min 2∙b , r≤max 2∙b, a, b, r>0 13

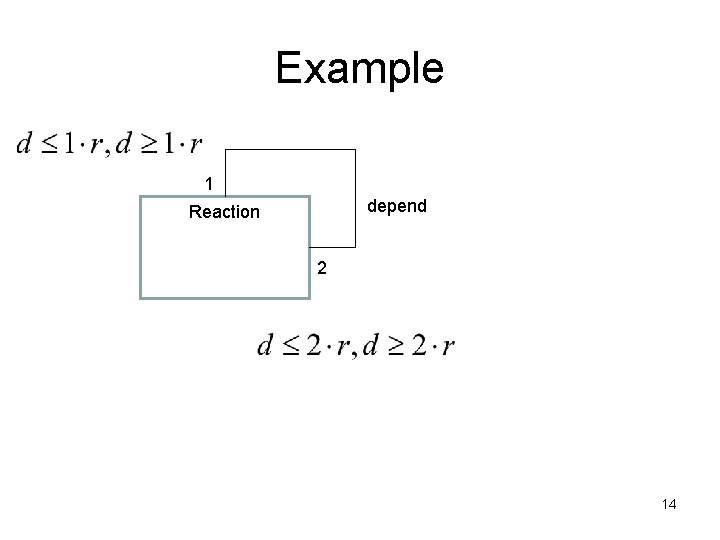
Example 1 depend Reaction 2 14

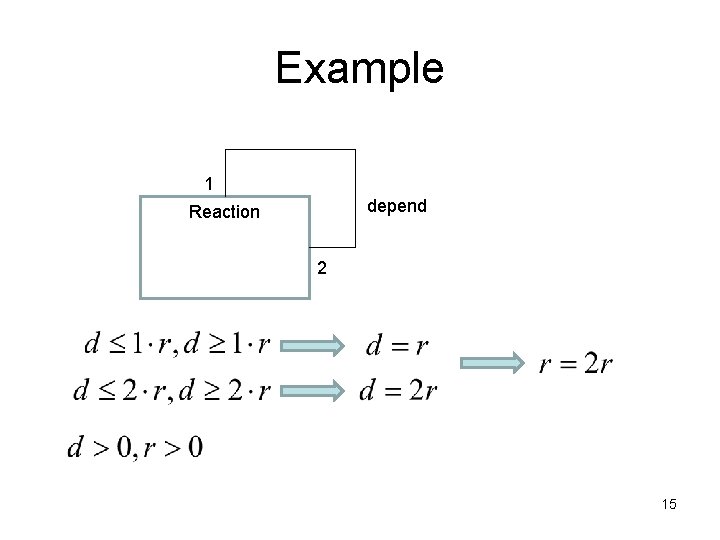
Example 1 depend Reaction 2 15

Calvanese and Lenzerini (94) – Extension with class hierarchies (1) • Calvanese and Lenzerini extend the method of Lenzerini and Nobily (92) to apply to schemata with class hierarchy. • The expansion is based on the assumption that class extensions may overlap. – Compound Class. – Compound relationship: 16

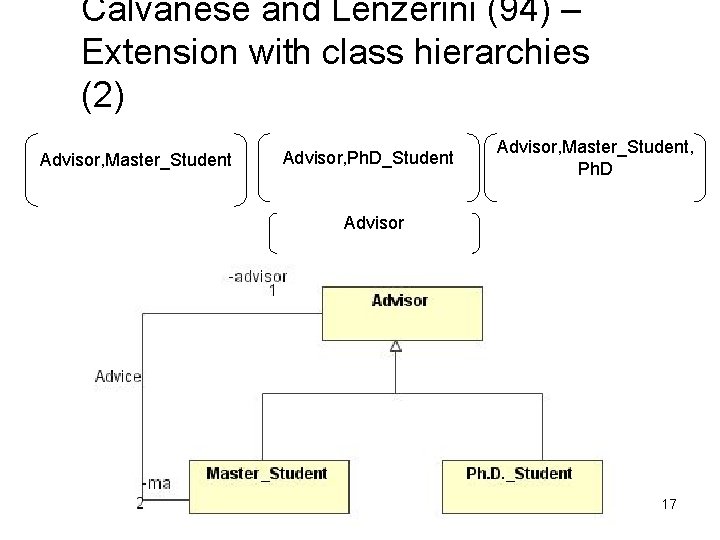
Calvanese and Lenzerini (94) – Extension with class hierarchies (2) Advisor, Master_Student Advisor, Ph. D_Student Advisor, Master_Student, Ph. D Advisor 17

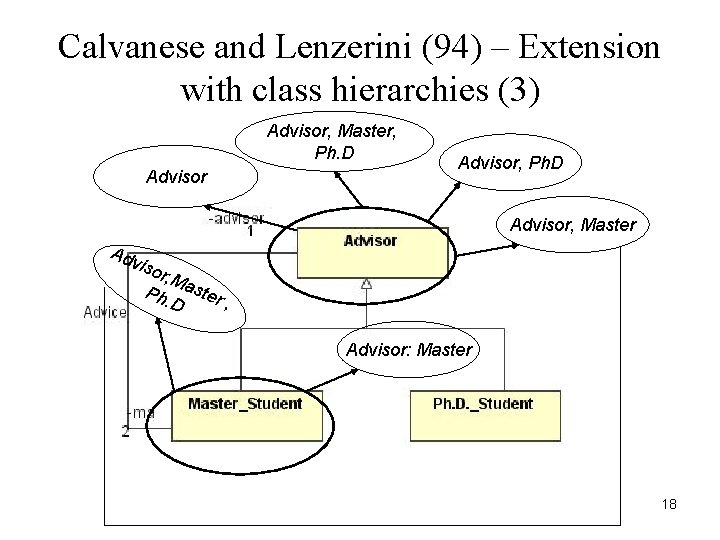
Calvanese and Lenzerini (94) – Extension with class hierarchies (3) Advisor, Master, Ph. D Advisor, Master Adv iso r, M Ph. aster D , Advisor: Master 18

Calvanese and Lenzerini (94) – Extension with class hierarchies (2) • For a class diagram with three classes and one association: 12 variables and 26 inequalities • An exponential number of variables. 19

Hardness of Finite Satisfiability • Berardi et al (2005) showed : • Lutz et al (2005) showed: 20

Agenda • • Background Reasoning Problems Previous works Research Contribution – Finite Satisfiability Method • Conclusions and Future Work 21

Finite. Sat Algorithm • The Finite. Sat Algorithm • Input: A class diagram CD with binary multiplicity constraints, class hierarchy constraints, and GS constraints. • Output: A linear inequality system ψCD • Method: 1. For every class, association, or multiplicity constraint: create variables and inequalities according to the Lenzerini and Nobili method. 2. For every class hierarchy constraint, B being the subclass with variable b and A being the super class with variable a, extend the inequality system with the inequalities a ≥ b. 3. For every GS constraint GS(C, C 1, . . . Cn; Const), C being the super-class, Cis being the subclasses, and Const being the GS constraint, extend the inequality system, as follows: 1. Const = disjoint: 2. Const = complete: 3. Const = incomplete: 4. Cons t= overlapping: Without inequality 5. Const = disjoint, incomplete: 6. Const = disjoint, complete: 7. Const = overlapping, complete: 8. Const = overlapping, incomplete: 22

The Finite. Sat Algorithm • Class hierarchy constrain A� B 23

GS Constraints -1 • For every GS constraint GS(C, C 1, . . . Cn; Const): 24

GS Constraints -2 • For every GS constraint GS(C, C 1, . . . Cn; Const): 25

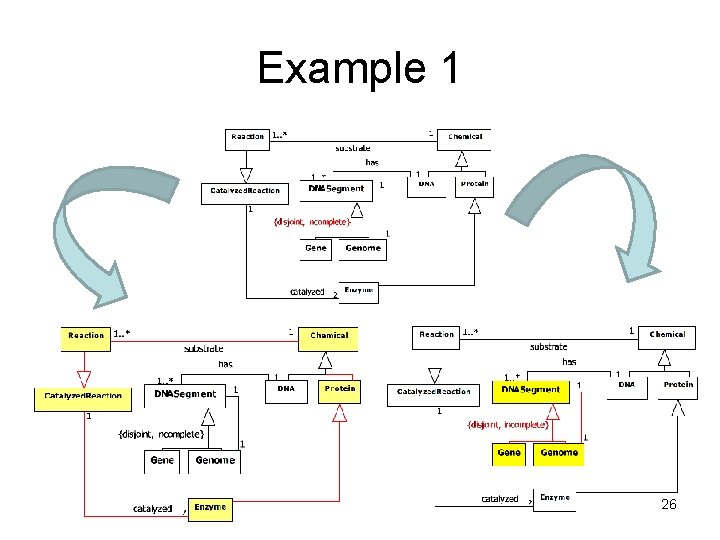
Example 1 26

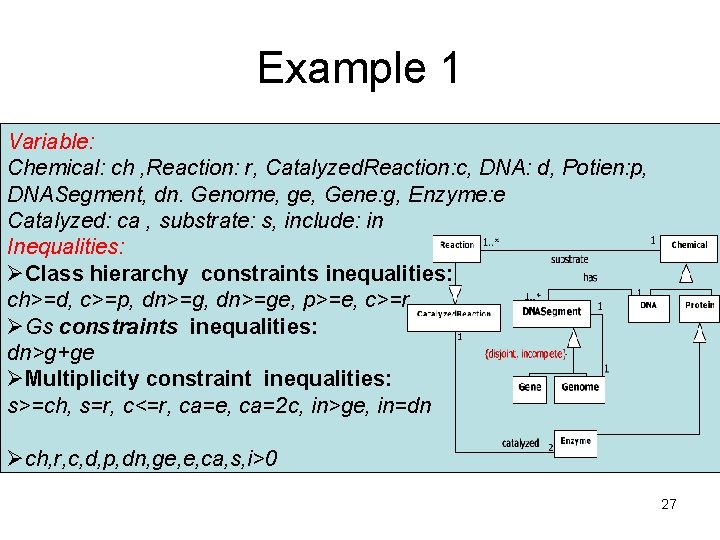
Example 1 Variable: Chemical: ch , Reaction: r, Catalyzed. Reaction: c, DNA: d, Potien: p, DNASegment, dn. Genome, ge, Gene: g, Enzyme: e Catalyzed: ca , substrate: s, include: in Inequalities: ØClass hierarchy constraints inequalities: ch>=d, c>=p, dn>=ge, p>=e, c>=r ØGs constraints inequalities: dn>g+ge ØMultiplicity constraint inequalities: s>=ch, s=r, c<=r, ca=e, ca=2 c, in>ge, in=dn Øch, r, c, d, p, dn, ge, e, ca, s, i>0 27

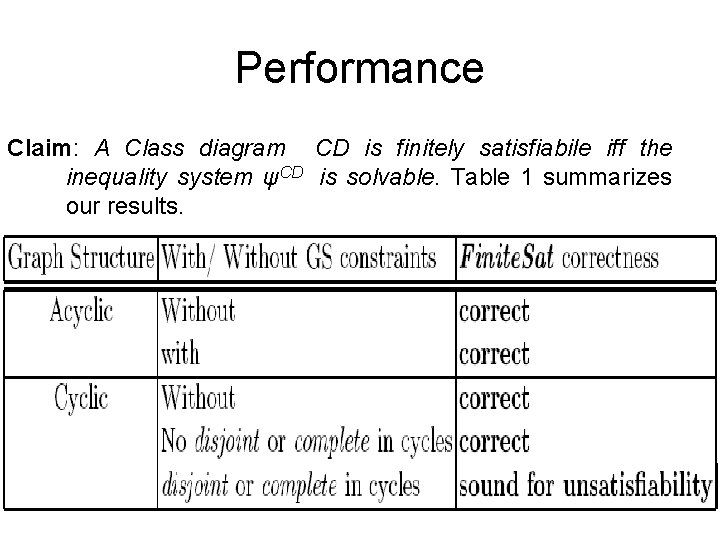
Performance Claim: A Class diagram CD is finitely satisfiabile iff the inequality system ψCD is solvable. Table 1 summarizes our results. 28

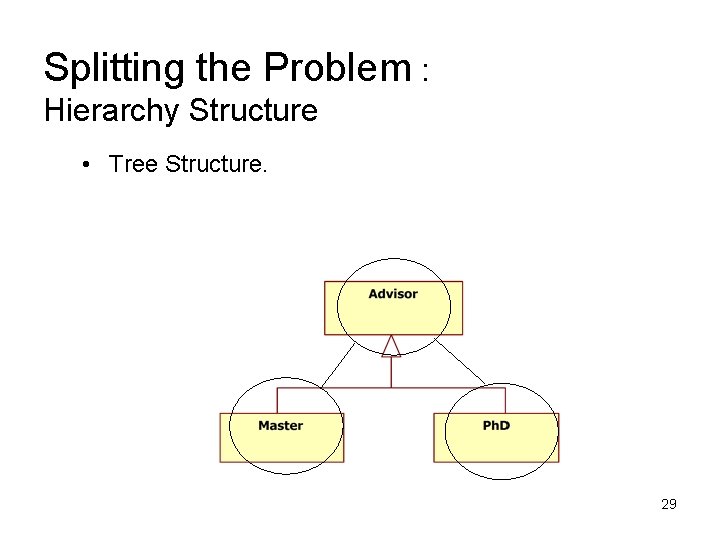
Splitting the Problem : Hierarchy Structure • Tree Structure. 29

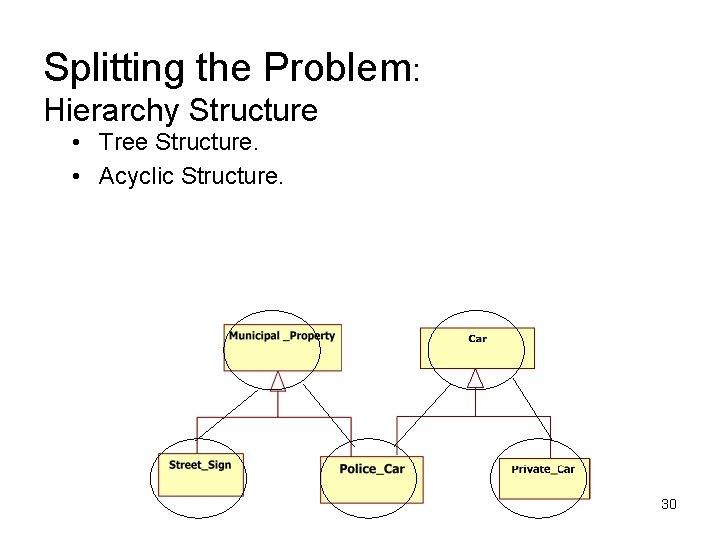
Splitting the Problem: Hierarchy Structure • Tree Structure. • Acyclic Structure. 30

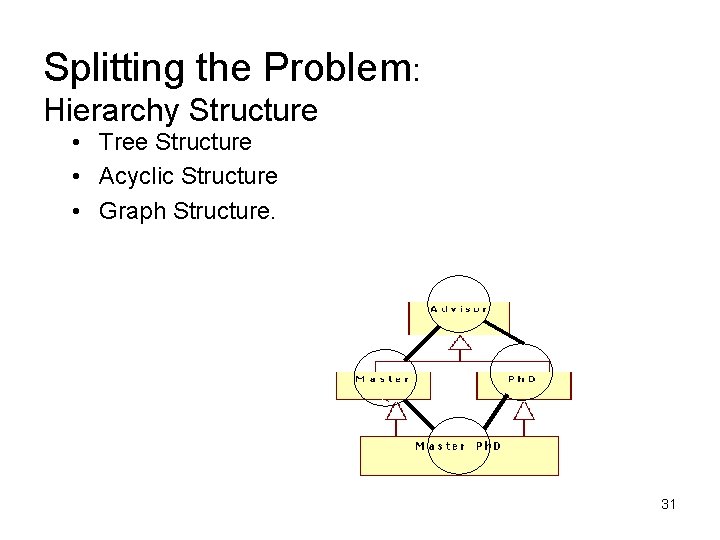
Splitting the Problem: Hierarchy Structure • Tree Structure • Acyclic Structure • Graph Structure. 31

Splitting the Problem Hierarchy Structure GS Constraint Tree Without Acyclic With Graph 32

Finite. Sat Extension to Qualifier • Qualifier A q 1 : Tq 1[tq 1] min. . max 1 1 … qn: Tqn[tqn] R min 2. . max 2 B – Imposes a partitioning on the set of related instances. – Tightens the multiplicity constraint of its association. – Can cause finite satisfiability problems.

Finite. Sat Extension to Qualifier Example TV-Network Day : Weekday 1 1 Weekday. Schedule Network. Schedule 1 Broadcast Schedule 1 Enum Week. Day = {Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, Saturday} • In every legal instance – Number of broadcast schedules, b, is 7*t, where t is the number of TV-Networks. At the same time t=b. The only solution for: • b=7 t • b=t Is empty or infinite!

Finite. Sat Extension to Qualifier – General case • If a combined domain value is non-finite, ignore the qualifier constraint, and handle like regular association. • Else, extend the inequality system with the following inequalities: – min 1 x b <= r <= max 1 x b – min 2 x a x tq 1 x … x tqn <= r <= max 2 x a x tq 1 x … x tqn

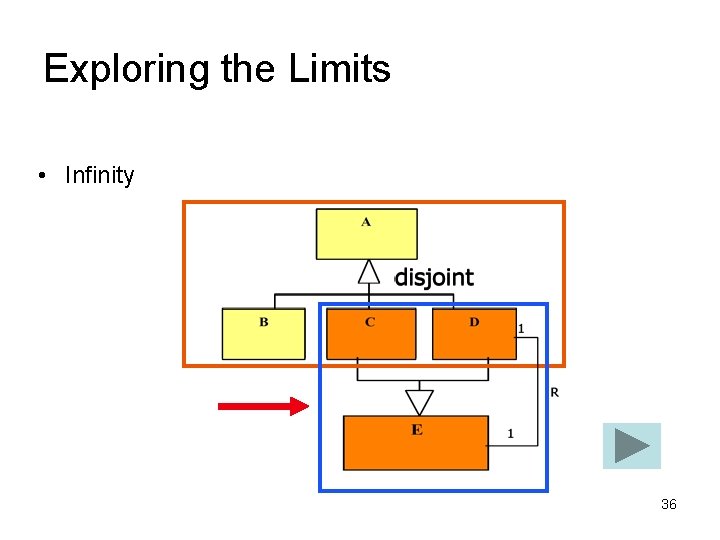
Exploring the Limits • Infinity 36

The Inequalities System There is a solution 37

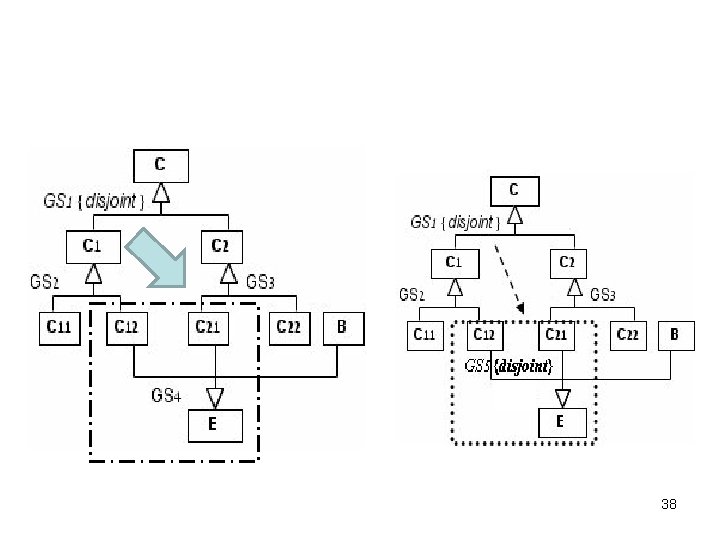
38

Future Work • Extensions: – Graph structure with disjoint, complete. – N-ary. – Aggregation. – Identification and Fixing (Sven Hartman, 2001) – integrate the implementation as add-in in existing case tool, 39

40

Backup Slides 41

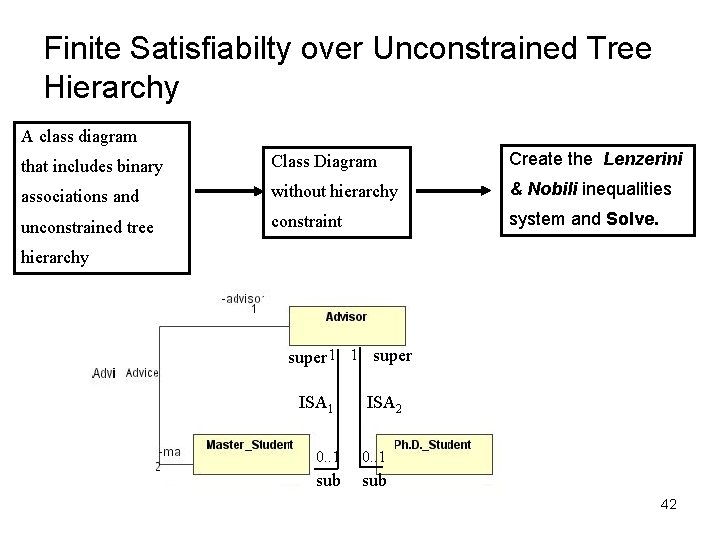
Finite Satisfiabilty over Unconstrained Tree Hierarchy A class diagram that includes binary Class Diagram Create the Lenzerini associations and without hierarchy & Nobili inequalities unconstrained tree constraint system and Solve. hierarchy super 1 1 super ISA 1 ISA 2 0. . 1 sub 42

Finite Satisfiabilty over Unconstrained Tree Hierarchy Claims • Claim [correctness]: A class diagram with unconstrained tree hierarchy is finitely satisfiable iff there exists a solution to the inequalities system. • Claim [Complexity]: Unconstrained Tree Hierarchy finite satisfiabilty method adds to the Lenzerini and Nobili method an O(n) time complexity, where n is the size of the class diagram (including associations, classes and class hierarchy constraints). 43

Finite Satisfiabilty over Unconstrained Tree Hierarchy Proof [Correctness Claim] CD: finitely satisfiable A class diagram that includes binary associations and unconstrained tree hierarchy CD’: finitely satisfiable Class Diagram Create the Lenzerini without hierarchy & Nobili inequalities constraint system and Solve. It is sufficient to show a reduction of the finite satisfiability problem for CD to finite satisfiability problem for CD’ without generalization sets. 44

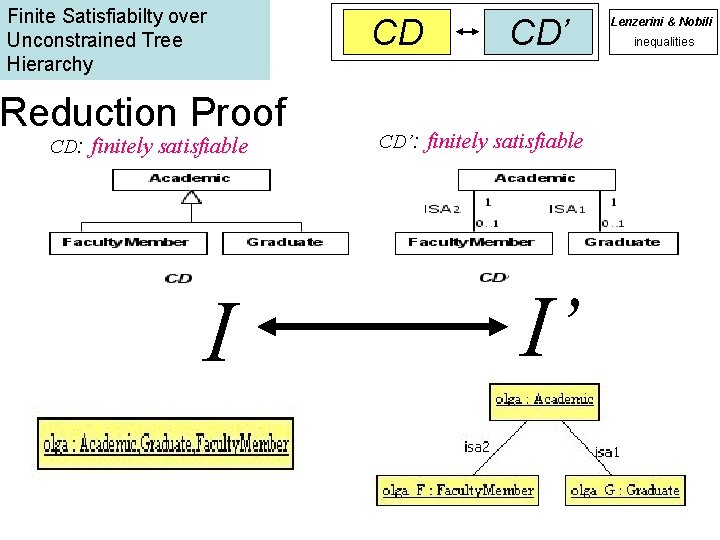
Finite Satisfiabilty over Unconstrained Tree Hierarchy Reduction Proof CD: finitely satisfiable I CD CD’ Lenzerini & Nobili inequalities CD’: finitely satisfiable I’ 45

Consistency notions (1) • Berardi et al (2005), distinguish two cases: – Consistency of class diagram – has an instantiation with at-least one non-empty class extension. – Class consistency – there is an instantiation in which the class extension is non-empty. The whole class diagram is consistent Consistent rest of the diagram 46

Consistency notions (2) • All class consistency of a class diagram – every class is consistent. • Full consistency of a class diagram – has an instance in which all class extensions are non-empty. 47

Finite satisfiability notions • All class finite satisfiability of a class diagram – every class there is a finite instance in which the class extension is non-empty (strong satisfiability, Lenzerini and Nobili, 1990). Research Contribution Lenzerini & Nobili 92 UML Class Diagram • Finite satisfiability of a class diagram – it has a finite instance in which all class extensions are non-empty. 48

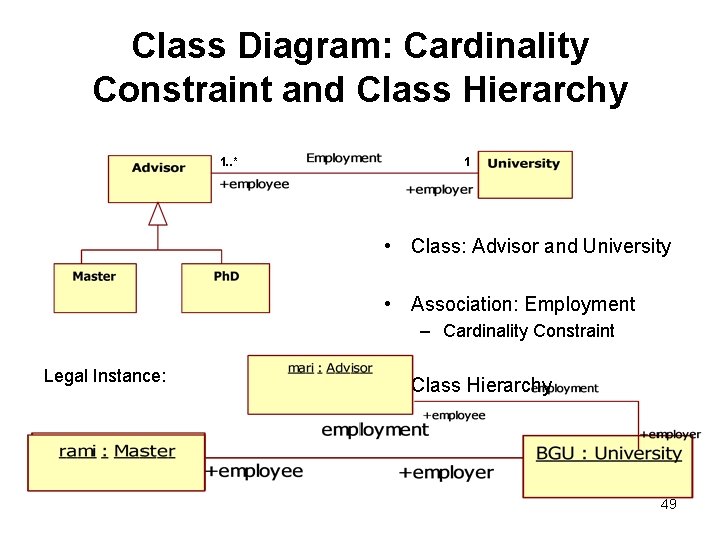
Class Diagram: Cardinality Constraint and Class Hierarchy 1. . * 1 • Class: Advisor and University • Association: Employment – Cardinality Constraint Legal Instance: • Class Hierarchy 49

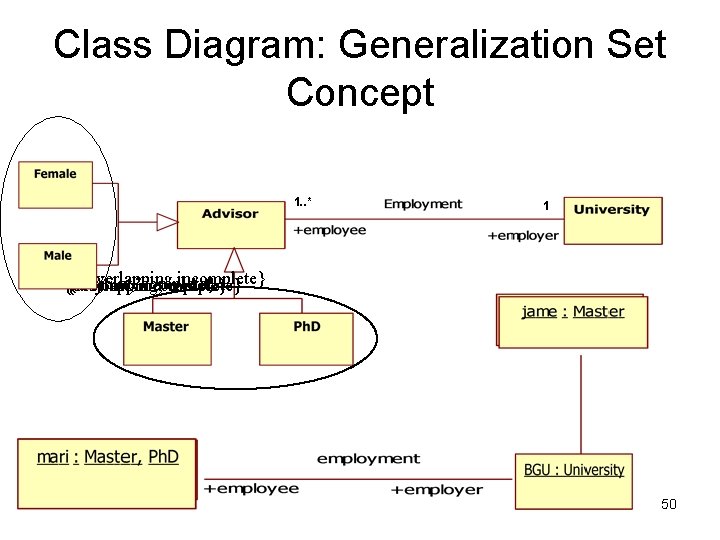
Class Diagram: Generalization Set Concept 1. . * 1 {overlapping, incomplete} {disjoint, complete} {overlapping, {disjoint, incomplete} 50