Efficient Processing of XML Twig Patterns with Parent

Efficient Processing of XML Twig Patterns with Parent Child Edges: A Look-ahead Approach Presenter: Qi He 1

Outline l ☞ XML Twig Pattern Matching ¡ Problem definition ¡ State of the Art: Twig. Stack ¡ Sub-optimality of Twig. Stack l Our algorithm Twig. Stack. List l Performance l Conclusion 2

XML Twig Pattern Matching l XML ¡ ¡ Data Model A XML document is commonly modeled as a rooted, ordered and labeled tree. E. g. Note that identifiers (e. g. b 1) are given to tree nodes for easy reference b 1 D 1: c 1 pf 1 preface p 1 paragraph t 1 title t 2 book s 1 p 2 f 1 paragraph figure section s 3 chapter …………. section s 2 section title c 2 chapter p 3 f 2 p 4 paragraph figure f 3 figure 3

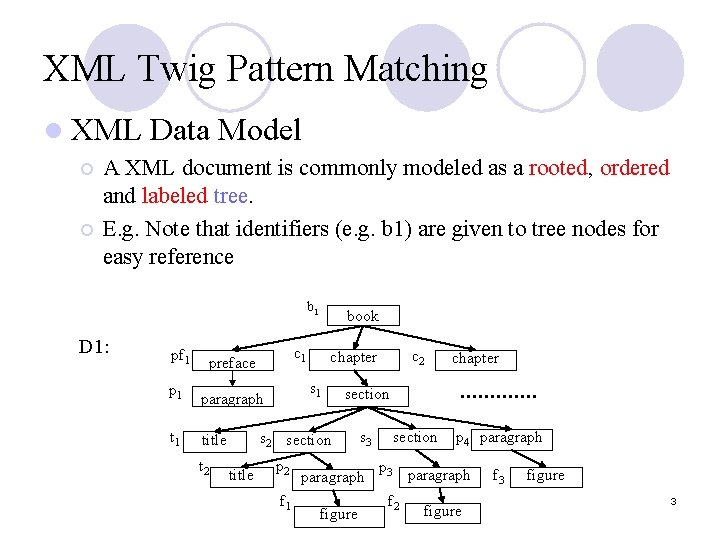
XML Twig Pattern Matching l Regional Coding [1] ¡ Node Label: (start. Pos: end. Pos, Level. Num) l l ¡ D 1: start. Pos and end. Pos are calculated by performing a pre-order traversal of the document tree; Level. Num is the level of the node in the tree. E. g. book (0: 50, 1) preface (1: 3, 2) chapter (4: 22, 2) section (5: 21, 3) paragraph (2: 2, 3) title: (6: 6, 4) title: (8: 8, 5) section(7: 12, 4) paragraph(9: 11, 5) figure (10: 10, 6) 1. chapter(23: 45, 2) section(13: 17, 4) paragraph(14: 16, 5) paragraph(18: 20, 4) figure (19: 19, 5) figure (15: 15, 6) M. P. Consens and T. Milo. Optimizing queries on files. In In Proceedings of ACM SIGMOD, 1994. 4

XML Twig Pattern Matching l What ¡ ¡ is a Twig Pattern? A twig pattern is a small tree whose nodes are predicates (e. g. element type test) and edges are either Parent-Child (P-C) edges or Ancestor-Descendant (A-D) edges. E. g. An XPath query Q 1 selects Figure elements which are descendants of some Paragraph elements which in turn are children of Section elements having at least one child element Title Q 1: Section[Title]/Paragraph//Figure Section Title Paragraph Figure 5

XML Twig Pattern Matching l Twig Pattern Matching ¡ Problem Statement l ¡ Given a query twig pattern Q, and a XML database D that has index structures (e. g. regional coding scheme) to identify database nodes that satisfy each of Q’s node predicates, compute ALL the answers to Q in D. E. g. The matches for twig pattern Section[Title]/Paragraph//Figure in the document D 1 are: (s 1, t 1, p 4, f 3) (s 2, t 2, p 2, f 1) b 1 D 1: c 1 pf 1 c 2 s 1 p 1 t 2 s 2 p 2 s 3 s 4 p 3 f 3 6 f 1 f 2

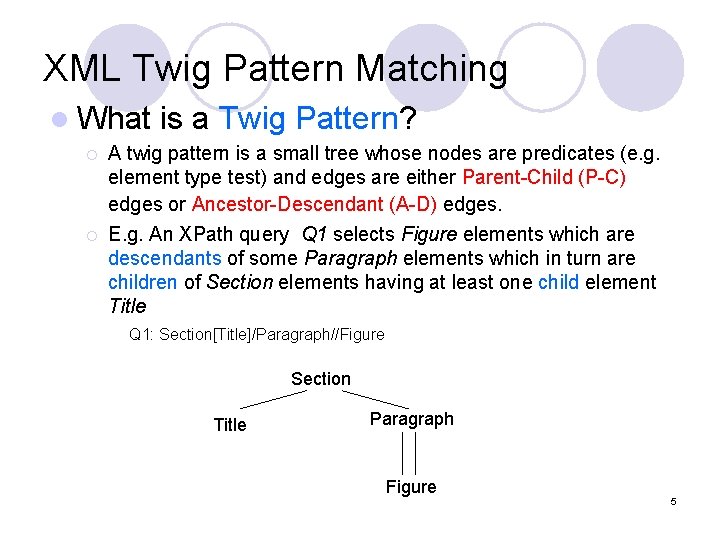
XML Twig Pattern Matching l Twig. Stack[2]: a holistic approach ¡ ¡ ¡ Tag Streaming: all elements of tag q are grouped in a stream Tq ordered by their start. Pos Optimal when all the edges in twig pattern are A-D edges Two-phase algorithm: l l 1. Phase 1 Twig. Join: a list of intermediate paths are outputted Phase 2 Merge: merge the intermediate path list to get the result N. Bruno, D. Srivastava, and N. Koudas. Holistic twig joins: optimal xml pattern matching. In In Proceedings of ACM SIGMOD, 2002. 7

XML Twig Pattern Matching l Twig. Stack Review ¡ ¡ A node q in a twig pattern Q is coupled with a stack Sq An element e is pushed into its stack if and only if e is in some match to Q. l l ¡ E. g. Only color highlighted elements are pushed into their stacks. Thus it is ensured that no redundant paths are output. An element e is popped out from its stack if all matches involving it have been reported l Thus we ensure that the memory space used by stacks is bounded. D 1: Q: Section[//Title]//Paragraph//Figure b 1 c 1 pf 1 SSection c 2 s 1 p 1 t 2 s 2 SParagraph s 3 s 4 p 2 p 3 f 1 f 2 f 3 STitle 8 SFigure

XML Twig Pattern Matching l Optimality of Twig. Stack for only A-D edge twig pattern ¡ ¡ Each stream Tq is scanned only once , where q appears the twig pattern No redundant intermediate result: All intermediate paths output in Phase 1 appear in the final result; l ¡ CPU and I/O cost: O(|Input| + |Output|) Space Complexity: O(|Longest Path in the XML tree|) 9

Sub-optimality of Twig. Stack Unfortunately, Twig. Stack is sub-optimal for queries with any parent-child relationship. l Twig. Stack may output a large size of intermediate results that are not merge-joinable to final solutions for queries with parent-child relationships. l 10

Example for sub-optimality of Twig. Stack An simple XML tree Twig Pattern s 1 t 1 Section p 1 title paragraph t 2 figure f 2 Twig. Stack output (s 1, t 1) as the intermediate result, since s 1 has a descendant t 1 and p 1 which in turn has a descendant f 2. l Observe that p 1 has no child with tag figure. There is not any matching in this XML tree. So (s 1, t 1) is a “useless” solution. l 11

Main problem and my experiment As shown before, Twig. Stack might output some intermediate results that are not merge-joinable to final solutions for queries with parent-child edges. l To have a better understanding , we perform Twig. Stack on real dataset. l Data set : Tree. Bank [UW XML repository] l Queries: l ¡ ¡ ¡ l Q 1: VP [/DT] //PRP_DOLLAR_ Q 2: S//NP[//PP/TO][/VP/_NONE_]/JJ Q 3: S [/JJ] /NP All queries contain parent-child relationships. 12

Our experimental results Intermediate paths Mergeby Twig. Stack joinable paths Q 1 10, 663 5 Percentage of useless intermediate paths 99. 9% Q 2 24, 493 49 99. 5% Q 3 70, 967 10 99. 9% Most intermediate paths do not contribute to final answers due to parent-child edges! It is a big challenge to improve Twig. Stack to answer queries with parent-child edges. 13

Our intuitive observation l We can improve Twig. Stack for queries in the previous example. An simple XML tree Twig Pattern s 1 t 1 Section p 1 title paragraph t 2 figure f 1 Our intuitive observation: why not read more paragraph elements and cache them in the main memory? l For example, in this XML tree, after we scan the p 1, we do not stop and continue to read the next element. Then we find that there is only one paragraph element and f 1 is not the child of paragraph. So we should not output any solution. 14 l

Outline l XML Twig Pattern Matching ¡ Problem definition ¡ State of the Art: Twig. Stack ¡ Sub-optimality of Twig. Stack l ☞ Our algorithm Twig. Stack. List l Experimental results l Conclusion 15

Our main idea Main idea: we read more elements in the input stream and cache some of them in the main memory so that we can make a more accurate decision about whether an element can contribute to final answer. l One desiderata: We cannot cache too many elements in the main memory. For each node q in twig query, the number of elements with tag q cached in the main memory should not be greater than the longest path in the XML dataset. l 16

Our caching strategy l What elements should be cached into the main memory? ¡ Only those that may contribute to final answers An simple XML tree Twig Pattern s 1 Section t 1 s 2 s 3 title paragraph s 4 p 1 We only need to cache s 1, s 2, s 4 into main memory, why not s 3? l Because if s 3 contributed to final answer, then there would be an element before p 1 that is child of s 3. Now we see that p 1 is the first 17 element. So s 3 is guaranteed not to contribute to final answer. l

Our criteria for pushing an element to stack l l l Whether an element can be pushed into stack is very important for controlling intermediate results. Why? Because, once an element is pushed into stack, then this element is ready to output. So less elements are pushed into stack, less intermediate results are output. Our Criteria: Given an element eq from stream Tq, before eq is pushed into stack Sq , we ensure that (i) element eq has a descendant eq’ for each child q’ of q, and (ii) if (q, q’) is a parent-child relationship, eq’ has parent with tag q in the path from eq to eqmax , where eqmax is the descendant of eq with the maximal start value. (iii) each of q’ recursively satisfy the first two conditions. 18

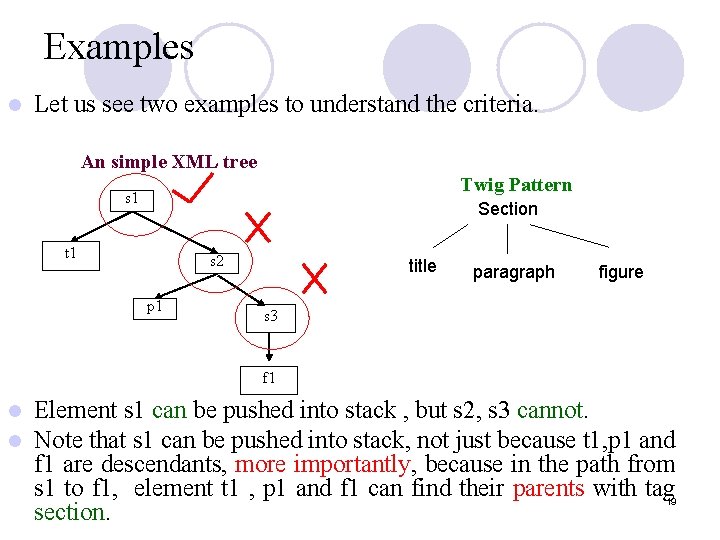
Examples l Let us see two examples to understand the criteria. An simple XML tree Twig Pattern s 1 Section t 1 s 2 p 1 title paragraph figure s 3 f 1 l l Element s 1 can be pushed into stack , but s 2, s 3 cannot. Note that s 1 can be pushed into stack, not just because t 1, p 1 and f 1 are descendants, more importantly, because in the path from s 1 to f 1, element t 1 , p 1 and f 1 can find their parents with tag section. 19

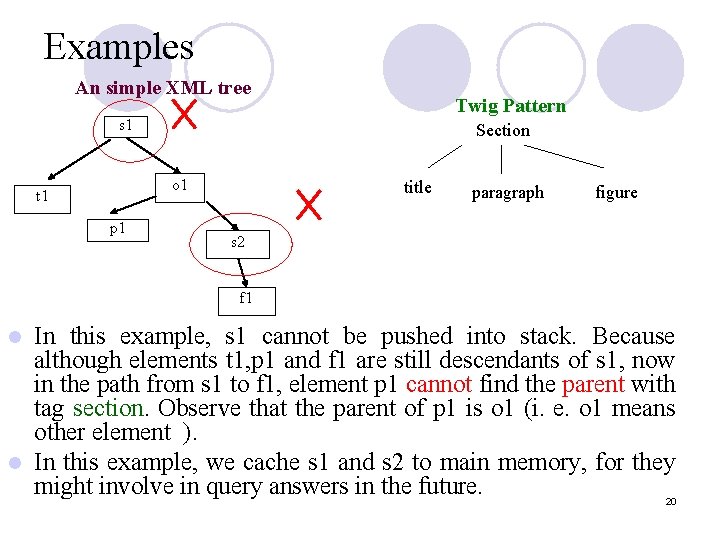
Examples An simple XML tree Twig Pattern s 1 Section o 1 t 1 p 1 title paragraph figure s 2 f 1 In this example, s 1 cannot be pushed into stack. Because although elements t 1, p 1 and f 1 are still descendants of s 1, now in the path from s 1 to f 1, element p 1 cannot find the parent with tag section. Observe that the parent of p 1 is o 1 (i. e. o 1 means other element ). l In this example, we cache s 1 and s 2 to main memory, for they might involve in query answers in the future. l 20

Twig. Stack. List l l We propose a novel holistic twig algorithm Twig. Stacklist to evaluate a twig query. Unlike previous Twig. Stack, Twig. Stack. List has the unique features: ¡ ¡ ¡ It considers the parent-child edge in the query and enhance the criteria for elements to be pushed into stack. It use data structure: list to cache some elements that likely participate in final solutions. The number of elements in any list is strictly bounded by the longest path in the dataset. It has a broader class of optimal queries. Twig. Stack. List can guarantee each output intermediate solution contributes to final answers when queries contain only ancestor-descendant edges below branching nodes. 21

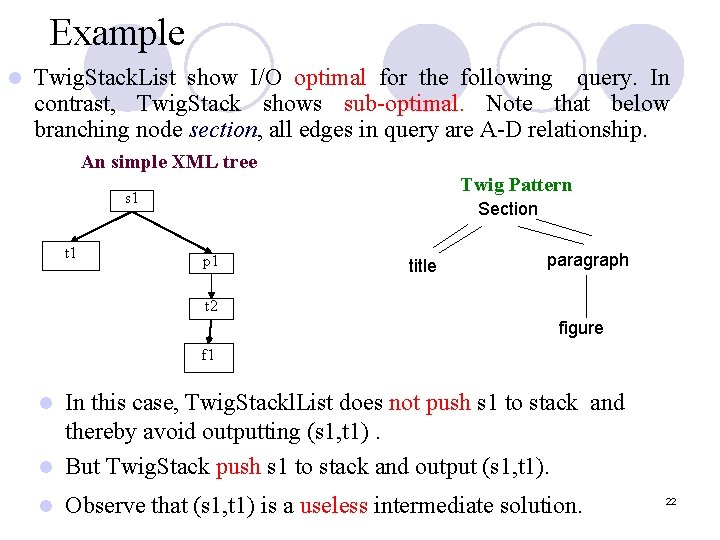
Example l Twig. Stack. List show I/O optimal for the following query. In contrast, Twig. Stack shows sub-optimal. Note that below branching node section, all edges in query are A-D relationship. An simple XML tree Twig Pattern s 1 t 1 Section p 1 title paragraph t 2 figure f 1 In this case, Twig. Stackl. List does not push s 1 to stack and thereby avoid outputting (s 1, t 1). l But Twig. Stack push s 1 to stack and output (s 1, t 1). l l Observe that (s 1, t 1) is a useless intermediate solution. 22

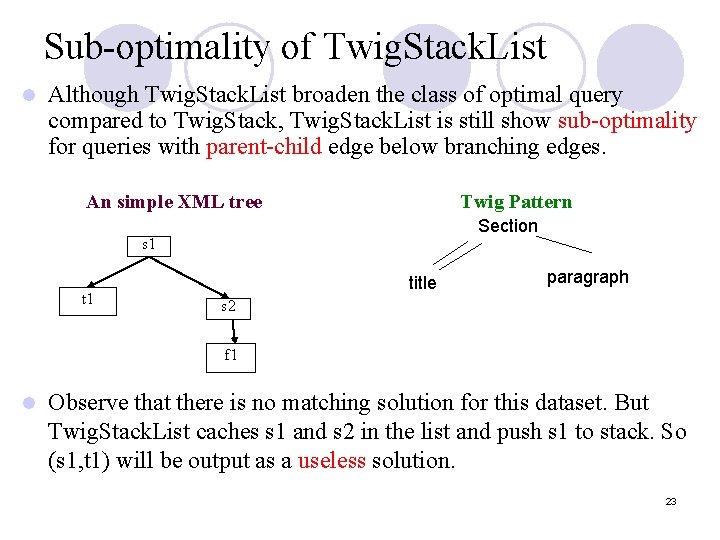
Sub-optimality of Twig. Stack. List l Although Twig. Stack. List broaden the class of optimal query compared to Twig. Stack, Twig. Stack. List is still show sub-optimality for queries with parent-child edge below branching edges. An simple XML tree Twig Pattern Section s 1 title paragraph s 2 f 1 l Observe that there is no matching solution for this dataset. But Twig. Stack. List caches s 1 and s 2 in the list and push s 1 to stack. So (s 1, t 1) will be output as a useless solution. 23

Outline l XML Twig Pattern Matching ¡ Problem definition ¡ State of the Art: Twig. Stack ¡ Sub-optimality of Twig. Stack l Our algorithm Twig. Stack. List l ☞ Experimental results l Conclusion 24

Experimental Setting l Experimental Setting ¡ ¡ Pentium 4 CPU, RAM 768 MB, disk 2 GB Tree. Bank l ¡ DTD data l l l ¡ Maximal depth 36, 2. 4 million nodes a → bc | cb |d c→a a and c are non- terminals, b and d are terminals Random l l Seven tags : a, b, c, d, e, f, g. ; uniform distributed Fan-out of elements varied 2 -100, depth varied 10 -100 25

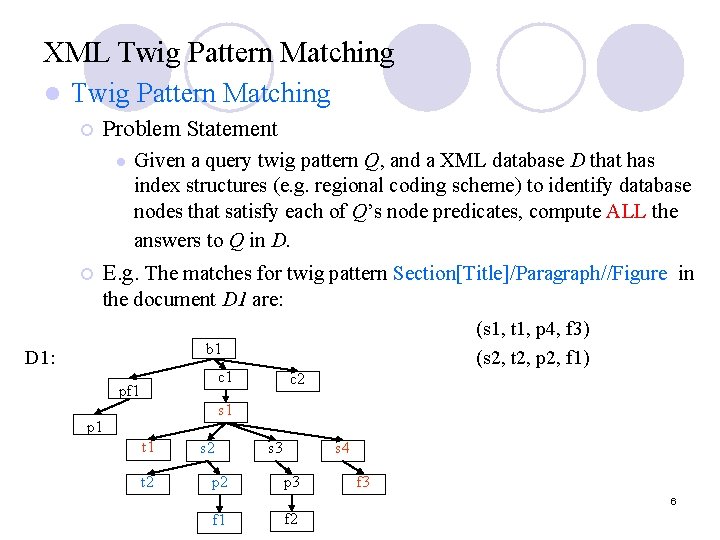
Performance against Tree. Bank l l Queries with XPath expression: Q 1 S[//MD]//ADJ Q 2 S/VP/PP[/NP/VBN]/IN Q 3 S/VP//PP[//NP/VBN]//IN Q 4 VP[/DT]//PRP_DOLLAR_ Q 5 S[//VP/IN]//NP Q 6 S[/JJ]/NP Number of intermediate path solutions for Twig. Stack. List V. s. Twig. Stack. List Reduction percentage Useful Path Q 1 35 35 0% 35 Q 2 2957 143 95% 92 Q 3 25892 4612 82% 4612 Q 4 10663 11 99. 9% 5 Q 5 702391 22565 96. 8% 22565 Q 6 70988 30 99. 9% 10 26

Performance analysis We have three observations: (1) when queries contain only ancestor-descendant edges, two algorithms have similar performance. See Q 1. l (2)When edges below non-branching nodes contain only ancestor-descendant relationships, Twig. Stack is optimal, but Twig. Stack show the sub-optimal. See Q 3. Q 5 l (3) When edges below branching nodes contain parent -child relationships, both Twig. Stack and Twig. Stack. List are sub-optimal. Buit Twig. Stack typically output far few “useless” intermediate solution than Twig. Stack. See Q 2, Q 4, Q 6. l l 27

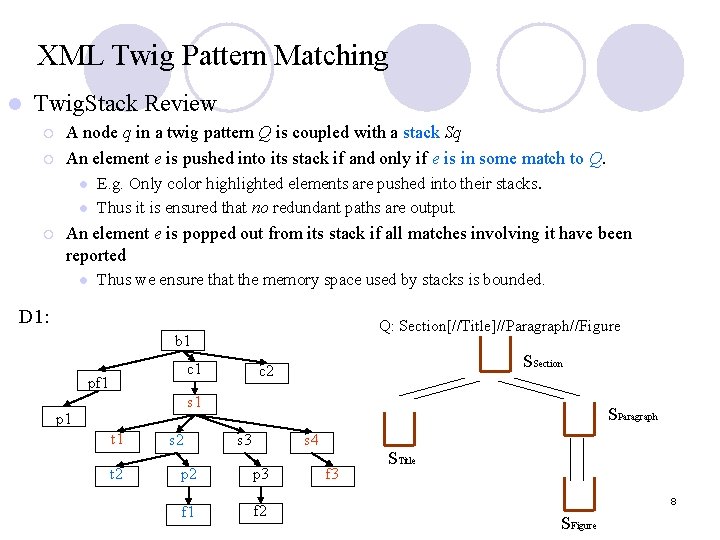
Performance against DTD data There is no matching solution for query a[//b]//c/d in the DTD dataset. But Twig. Stack outputs too much redundant path solutions. In contrast, Twig. Stack. List shows its optimal and significantly outperforms Twig. Stack in this query. 28

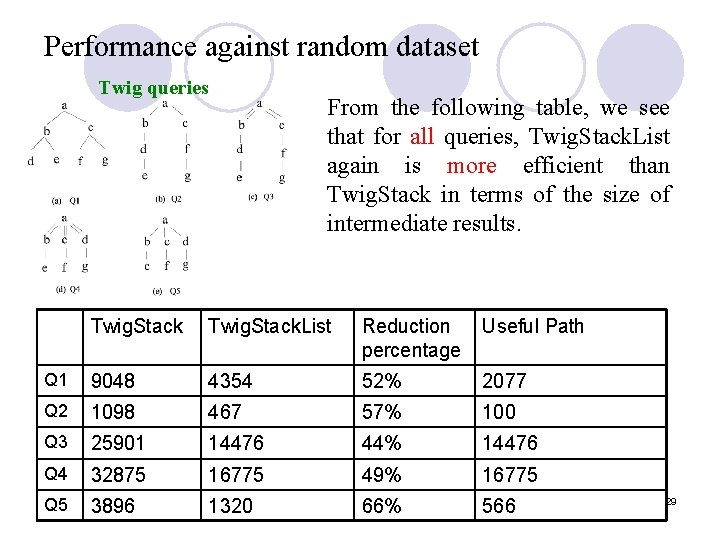
Performance against random dataset Twig queries From the following table, we see that for all queries, Twig. Stack. List again is more efficient than Twig. Stack in terms of the size of intermediate results. Twig. Stack. List Reduction percentage Useful Path Q 1 9048 4354 52% 2077 Q 2 1098 467 57% 100 Q 3 25901 14476 44% 14476 Q 4 32875 16775 49% 16775 Q 5 3896 1320 66% 566 29

Outline l XML Twig Pattern Matching ¡ Problem definition ¡ State of the Art: Twig. Stack ¡ Sub-optimality of Twig. Stack l Our algorithm Twig. Stack. List l Experimental results l ☞ Conclusion 30

Conclusion l l l Previous algorithm Twig. Stack show the suboptimality for queries with parent-child edges. We propose new algorithm Twig. Stack. List to address this problem. Twig. Stack. List broadens the class of query with I/O optimality. Experiments show that Twig. Stack. List typically output much fewer useless intermediate result as far as the query contains parent-child relationships. We commend to use Twig. Stack. List to evaluate a query with parent-child relationships. 31

Backup questions: l 1. Turn back to the slide about “Performance against DTD data”. In two figures , what is the X-axis? l l X-axis shows that the ratio of the number of elements with tag d relative to that with b and c. This ratio is important. Because according to the DTD: a → bc | cb |d , c → a, for query a[//b]//c/d, while the ratio decreases, the “useless” intermediate results output by Twig. Stack increase. In contrast, Twig. Stack. List is optimal in this case. So it does not affected by the variety of the ratio. Therefore, we show the superiority of Twig. Stack. List over Twig. Stack by varying the ratio. 32

Backup questions: l 2. You say that Twig. Stack. List is more efficient than Twig. Stack, since it outputs less intermediate results. So it is easy to understand that Twig. Stack. List is better than Twig. Stack in terms of I/O cost, but how about CPU cost? l l Twig. Stack. List is more efficient than Twig. Stack for evaluating query with parent-child relationships in terms of not only intermediate result size, but also the execution time. Of course, Twig. Stack. List needs to scan the elements cached in the main memory and slightly increase the CPU cost. But compared to the great benefit from the reduction of I/O cost, this cost is worthy. 33