Efficient Policy Gradient OptimizationLearning of Feedback Controllers Chris

Efficient Policy Gradient Optimization/Learning of Feedback Controllers Chris Atkeson

Punchlines • Optimize and learn policies. Switch from “value iteration” to “policy iteration”. • This is a big switch from optimizing and learning value functions. • Use gradient-based policy optimization.

Motivations • Efficiently design nonlinear policies • Make policy-gradient reinforcement learning practical.

Model-Based Policy Optimization • Simulate policy u = π(x, p) from some initial states x 0 to find policy cost. • Use favorite local or global optimizer to optimize simulated policy cost. • If gradients are used, they are typically numerically estimated. • Δp = -ε ∑x 0 w(x 0)Vp 1 st order gradient • Δp = -(∑x 0 w(x 0)Vpp)-1 ∑x 0 w(x 0)Vp 2 nd order

Can we make model-based policy gradient more efficient?

Analytic Gradients • Deterministic policy: u = π(x, p) • Policy Iteration (Bellman Equation): Vk-1(x, p) = L(x, π(x, p)) + V(f(x, π(x, p)), p) • Linear models: f(x, u) = f 0 + fxΔx + fuΔu L(x, u) = L 0 + LxΔx + LuΔu π(x, p) = π0 + πxΔx + πpΔp V(x, p) = V 0 + VxΔx + VpΔp • Policy Gradient: Vxk-1 = Lx + Luπx + Vx(fx + fuπx) Vpk-1 = (Lu + Vxfu)πp + Vp

Handling Constraints • Lagrange multiplier approach, with constraint violation value function.

Vpp: Second Order Models

Regularization

LQBR: Linear (dynamics) Quadratic (cost) Bilinear (policy) Regulator

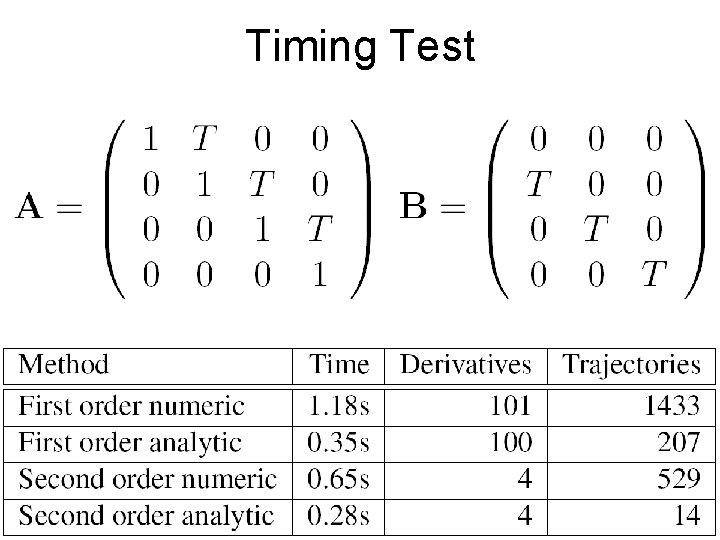
Timing Test

Antecedents • Optimizing control “parameters” in DDP: Dyer and Mc. Reynolds 1970. • Optimal output feedback design (1960 s 1970 s) • Multiple model adaptive control (MMAC) • Policy gradient reinforcement learning • Adaptive critics, Werbos: HDP, DHP, GDHP, ADHDP, ADDHP

When Will LQBR Work? • Initial stabilizing policy is known (“output stabilizable”) • Luu is positive definite. • Lxx is positive semi-definite and (sqrt(Lxx), Fx) is detectable. • Measurement matrix C has full row rank.

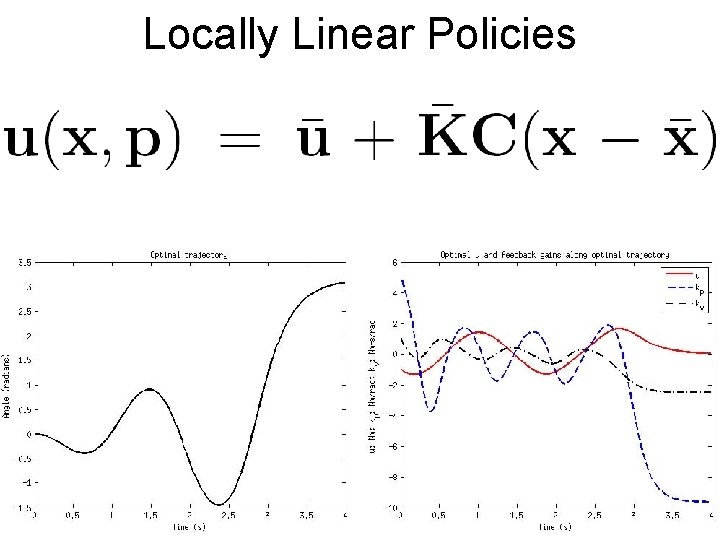
Locally Linear Policies

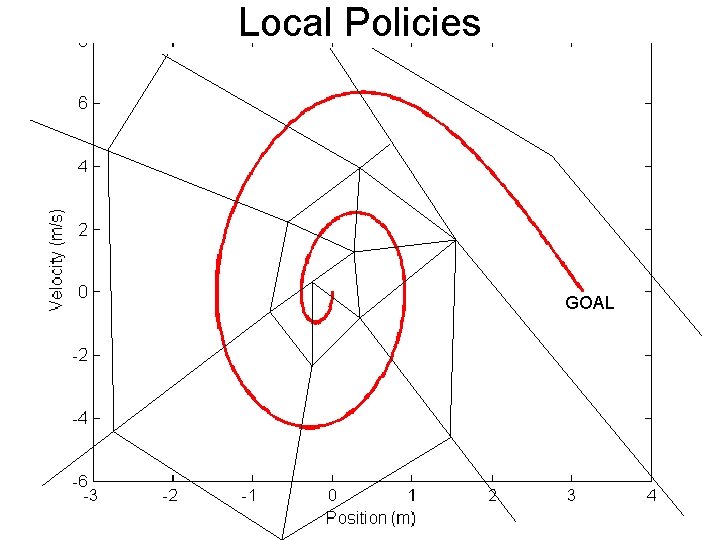
Local Policies GOAL

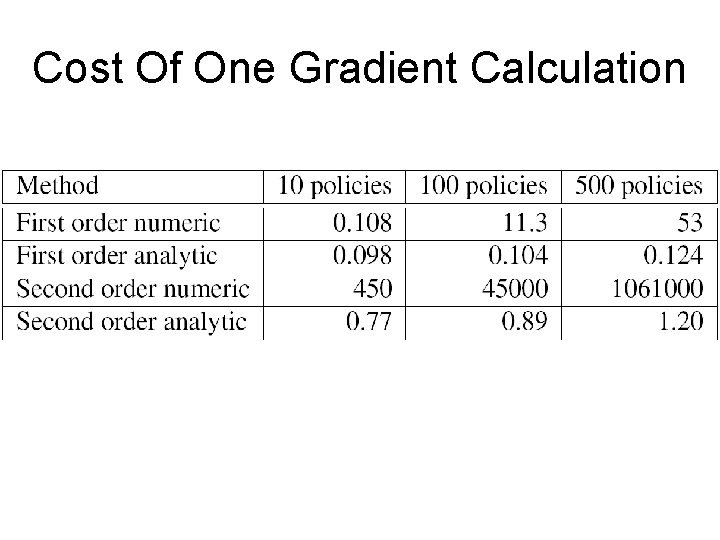
Cost Of One Gradient Calculation

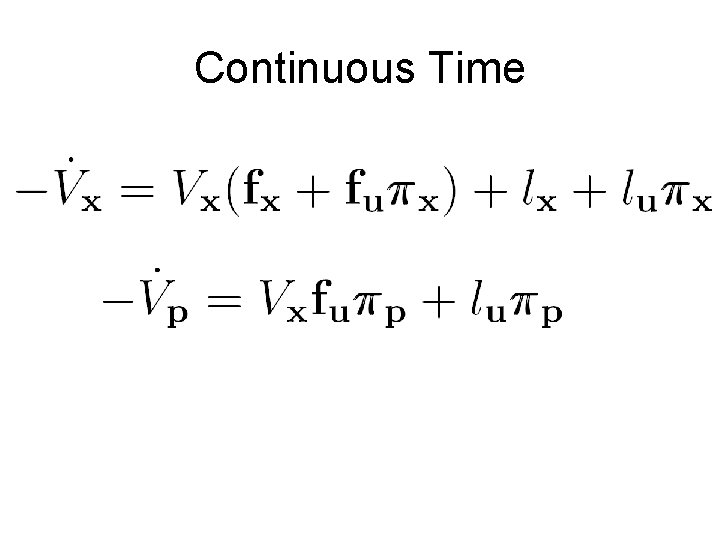
Continuous Time

Other Issues • • • Model Following Stochastic Plants Receding Horizon Control/MPC Adaptive RHC/MPC Combine with Dynamic Programming Dynamic Policies -> Learn State Estimator

Optimize Policies • Policy Iteration, with gradient-based policy improvement step. • Analytic gradients are easy. • Non-overlapping sub-policies make second order gradient calculations fast. • Big problem: How choose policy structure?