Efficient multiplier for GF2 m defined by the

Efficient multiplier for GF(2 m) defined by the all one polynomial and trinomial Ku-Young Chang, Information Security Infrastructure Research group

Outline I Introduction Overview of multiplier in GF(2 m) Normal basis Polynomial basis II Bit-parallel multiplier for GF(2 m) defined by all one polynomial Hybrid multiplier for GF(2 m) defined III by an irreducible trinomial Proprietary 정보보호기반그룹 2

Overview of multiplier for GF(2 m)(1/2) ▣ Application of arithmetic operation in GF(2 m) ◈ Coding theory, computer algebra, public key cryptosystem ◈ ECC requires efficient operation over a large finite field ▣ Multiplication is a core operation in GF(2 m) ◈ Exponentiation and multiplicative inversion can be carried out by iterative multiplication ◈ Hardware implementation of arithmetic operations in GF(2 m) requires an efficient design of multiplier ▣ The efficiency of multiplication depends on the choice of basis ◈ Normal basis, Polynomial basis, Dual basis Proprietary 정보보호기반그룹 3

Overview of multiplier for GF(2 m) (2/2) ▣ Efficiency of multiplier ◈ Space complexity : the number of XOR and AND gates ◈ Time complexity : the total gate delay of the circuit ▣ Type of multiplier Bit-parallel multiplier Logic gate Bit-serial multiplier Logic gate m iteration Output ( Parallel-out) Proprietary Output 정보보호기반그룹 4

Normal basis ▣ For , let ◈ N is called the normal basis of GF(2 m) over GF(2) ◈ ◈ It is well known that there exists a normal basis for GF(2 m) over GF(2) ◈ – Squaring in the normal basis representation can be performed by a right cyclic shift without using any gate ◈ But, the multiplication in the normal basis except for optimal normal basis(ONB) is more complex than multiplication in polynomial basis Proprietary 정보보호기반그룹 5

Optimal Normal basis ▣ ONB was introduced by Mullin et al. in order to reduce the hardware complexity of multiplying field elements in GF(2 m) ◈ There exists two types of ONB called ONB type I and ONB type II ▣ ONB type I ◈ m+1 is prime, and 2 is primitive modulo m+1; then the nontrivial (m+1)st roots of unity form an ONB of GF(2 m) over GF(2) ▣ ONB Type II ◈ 2 is primitive modulo 2 m+1, and ◈ Either – 2 is primitive root modulo 2 m+1 or – 2 m+1 = 3 mod 4 and the multiplication order of 2 modulo 2 m+1 is m ; ◈ Then where Proprietary generates an ONB of GF(2 m) over GF(2), is a primitive (2 m+1)st root of unity 정보보호기반그룹 6

Gaussian Normal basis ▣ Gaussian normal basis(GNB) is a generalization of ONB ▣ Type T GNB ◈ Let m be a positive integer not divisible by 8, and let T be a positive integer ◈ A type T GNB for GF(2 m) exists p = Tm+1 is prime and gcd(Tm/k, m)=1, where k is the multiplicative order of 2 modulo p ◈ T is a positive integer measuring the complexity of the multiplication operation with the respect to that basis ◈ For a given T and m, GF(2 m) can have at most one GNB of type T ▣ NIST has recommended five GF(2 m) fields for ECDSA, that is m { 163, 233, 283, 409, 571} ◈ GF(2163) : Type 4, GF(2233) : Type 2, GF(2283) : Type 6, GF(2409) : Type 4, GF(2571) : Type 10 Proprietary 정보보호기반그룹 7

Polynomial basis ▣ Let f(x) be an irreducible polynomial of degree m over GF(2 m) and GF(2 m) be a root of f(x) ◈ forms a basis of GF(2 m) over GF(2) and is called the polynomial basis ▣ We can always choose an irreducible trinomial basis or pentanomial basis over GF(2) ◈ Trinomial over GF(2): ◈ Pentanomial over GF(2): , where ▣ The field defined by an irreducible trinomial are frequently used in application containing ECC ◈ But, it does not always exist a trinomial basis ◈ For example, trinomial basis does not exist in GF(2163) used mainly to ECC ◈ In this case, irreducible pentanomial are suggested Proprietary 정보보호기반그룹 8

Outline I Introduction II Bit-parallel multiplier for GF(2 m) defined by all one polynomial Redundant representation Multiplier based on redundant representation Hybrid multiplier for GF(2 m) defined III by an irreducible trinomial Proprietary 정보보호기반그룹 9

Redundant representation(1/2) ▣ Consider of degree m over GF(2) which is called the all-one polynomial(AOP) ◈ AOP f(x) is irreducible modulo m+1 is prime and 2 is primitive ◈ That is, GF(2 m) defined by AOP is ONB type I ◈ Note that m is even ◈ Let Proprietary be a root of f(x) 정보보호기반그룹 10

Redundant representation(2/2) ▣ We introduce the set expanding polynomial basis which is called a redundant representation of GF(2 m) over GF(2) ◈ Modular reduction in the redundant representation is more efficient than that in other basis – For b GF(2 m), shift of b *b can be computed by an k-fold right cyclic ◈ Squaring in the redundant representation can be performed by a simple rewiring Proprietary 정보보호기반그룹 11

Multiplier based on redundant representation(1/4) ▣ Let be the root of the irreducible AOP of degree m over GF(2) and let m = 2 n ◈ ◈ We partition – ◈ Using BC + we obtain AD = (A+B)(C+ D) + AC + – P 1 = AC + BD + ( AC + – P 2 = ( A+B )( C+ D) Proprietary BD, BD ) 정보보호기반그룹 12

Multiplier based on redundant representation(2/4) ▣ Computation of P 1 ◈ AC + BD requires 2 n(n+1) AND gates, 2 n 2 -1 XOR gates, and TA + TX delays – Here TA and TX are the delay of one AND gate and one XOR gate, respectively ◈ Since ( AC + BD ) can be computed by an n-fold right cyclic shift of AC + BD, it can be obtained by a simple rewiring without using any gates ◈ P 1 requires 2 n(n+1) AND gates, 2 n 2+2 n XOR gates, and TA + (1+ ) TX delays Proprietary 정보보호기반그룹 13

Multiplier based on redundant representation(3/4) ▣ Computation of P 2 ◈ A+B and C+ D can be implemented by a parallel computation ◈ P 2 requires (n+1)2 AND gates, n 2+2 n XOR gates, and TA + ( 1 + ) TX delays ▣ Since P 1 and P 2 have the same time delay, then P 1 can be computed in parallel with P 2 ▣ Finally, we add P 1 and P 2 Proprietary a b P 1 a · b P 2 Parallel computation 정보보호기반그룹 14

Multiplier based on redundant representation(4/4) ▣ The proposed multiplier for GF(2 m) defined by AOP requires about 25 percent fewer AND/XOR gates than the previously proposed multiplier using AOP, while it has almost the same time delay as the previously proposed one ◈ IEEE Transactions on Computers, to appear 2005 Comparison of bit parallel multiplier for GF(2 m) defined by AOP Proprietary 정보보호기반그룹 15

Outline I Introduction II Bit-parallel multiplier for GF(2 m) defined by all one polynomial Hybrid multiplier for GF(2 m) defined III by an irreducible trinomial Objective of hybrid Multiplier Partial multiplier Hybrid multiplier Comparison Proprietary 정보보호기반그룹 16

Objective of hybrid multiplier ▣ A trade-off between performance and area is important to design an efficient hardware structure for arithmetic operation in GF(2 m) ◈ The bit-serial method – small size of hardware – repeated operation more than m times which is reduce the system performance ◈ The bit-parallel method – high performance – according to enlargement of the degree m, its hardware area increase asymptotically with m 2 ==> the hybrid multiplier for GF(2 m) defined by an irreducible trinomial ◈ constructed in variable structure depending on the performance area trade-off Proprietary 정보보호기반그룹 17

Partial multiplier(1/3) ▣ Let f(x) = ( ) be an irreducible trinomial of degree m over GF(2) ▣ Consider the partial multiplication of and for any k<m ◈ is represented by the following matrix M ◈ Using the relation , if , the terms with degree larger than m-1 can be reduced only once Proprietary 정보보호기반그룹 18

Partial multiplier(2/3) ▣ By this reduction, each m+i th row of M for added to the i th and n+i th rows of M ▣ If Z is the matrix obtained from M after the above reduction process, we can decompose Z as the sum of three matrices X, T, and U, i. e. Z = X+T+U Proprietary is 정보보호기반그룹 19

Partial multiplier(3/3) ▣ Any i th row of Z can be obtained from the n th row of z by rewiring without using any gates ▣ n th row Zn of Z is computed by the following equation ◈ We need k-1 XOR gates and TX delay in order to compute Zn ▣ Since Z is an matrix, Z b requires km AND gates, (k 1)m XOR gates, and TA+ )TX delays ◈ b = ( b 0, b 1, … , bk-1 )t Proprietary 정보보호기반그룹 20

Hybrid multiplier(1/2) ▣ Let and. To compute a(x)b(x) mod f(x), we use the partial multiplication ▣ We first obtain the matrix Z from the matrix M and then partition b(x) into k-bit elements by the following method ( bi = 0 for ) where ◈ a(x)b(x) mod f(x) = a(x)( Proprietary ) mod f(x) 정보보호기반그룹 21

Hybrid multiplier(2/2) ▣ If s = , then a(x)Ts is added to a(x)Ts-1 after the following k-bit reduction process ---(1) ▣ We obtain a(x)(Ts + Ts-1) by adding (1) to a(x)Ts-1 ▣ Finally, we can compute a(x)(Ts + Ts-1 + … + T 0 ) by iterating these process ▣ The proposed hybrid multiplier requires km AND gats, km+2 k-1 XOR gates, and TX+ ( max{TA, TX} + TX ) delays Proprietary 정보보호기반그룹 22

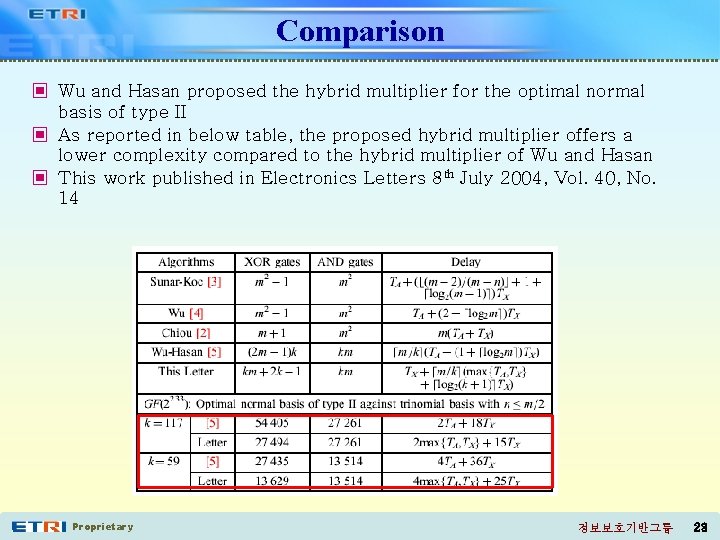
Comparison ▣ Wu and Hasan proposed the hybrid multiplier for the optimal normal basis of type II ▣ As reported in below table, the proposed hybrid multiplier offers a lower complexity compared to the hybrid multiplier of Wu and Hasan ▣ This work published in Electronics Letters 8 th July 2004, Vol. 40, No. 14 Proprietary 정보보호기반그룹 23

Conclusion ▣ We proposed the efficient two multiplier for GF(2 m) ◈ Lower complexity bit-parallel multiplier for GF(2 m) defined by AOP ◈ Hybrid multiplier for GF(2 m) defined by an irreducible trinomial ▣ We show that the proposed multiplier is more efficient than the previously proposed ones ▣ Recently, Fan and Dai introduced the shift polynomial basis in order to the design of the efficient multiplier for GF(2 m) defined by an irreducible trinomial ◈ In future work, we need to design the efficient pentanomial basis multiplier using the shift polynomial basis ◈ Also, we need to study a hybrid multiplier for GF(2 m) defined by an irreducible pentanomial Proprietary 정보보호기반그룹 24