Efficient Maximal Pattern Discovery from Massive Geometric Graphs

大規模幾何データからの高速な 極大部分グラフ発見 Efficient Maximal Pattern Discovery from Massive Geometric Graphs 有村博紀 宇野毅明 下薗真一 北海道大学 大学院情報科学研究科 国立情報学研究所 九州 業大学情報 学部 This work is partly supported by MEXT Grant-in-Aid for Scientific Research for Specially Promoted Research on “Semi-structured Data Mining”

Backgrounds �Rapid growth of both the amount and the varieties of nonstandard datasets in scientific, spatial, and relational domains. �There are increasing demands for efficient methods to extract useful patterns and rules from weakly structured datasets. �Graph Mining…

Graph mining �Finding interesting subgraphs appearing in an input collection of labeled graphs. �One of the most promising approaches for knowledge discovery from weakly structured datasets. �A most popular approach is frequent subgraph mining [Inokuchi et al. 2000], but it can often generate a huge number of redundant subgraphs, which degrate the efficiency and the comprehensiveness very much. �How to cope with this proplem. . .

Knowledge Discovery from Geometric Data �Network data with geometric information ◦ Chemical compound with 2 D or 3 D information on their atoms and edges [Kuramochi and Karypis [ICDE’ 02] ◦ CIty map with infrastructure information Geographic Information Systems (GIS) ◦ VLSI layout with chips and wires �Geometric graphs. . .

Geometric matching �P matches Q iff P is geometrically isomorphic to a subgraph of Q �Defined through the invariance under a class of “rigid” geometric transformations and graph isomorphism. y A A 2. 0 A A g g g A g g 1. 0 A 2. 0 3. 0 x g g g A

Maximal pattern discovery problem �A maximal pattern is a geometric graph which is not included in any properly larger subgraph having the same set of occurrences in D. �The maximal subgraph mining problem asks to find all maximal patterns (closed patterns) appearing in a given input geometric graph D without repetition �The set M of all maximal patterns is expected to be much smaller than the set F of all frequent patterns

Difficulties in maximal pattern mining �A number of efficient maximal pattern algorithms are proposed for sets, sequences, and graphs [3, 9, 20, 22, 25]. ◦ Some algorithms use explicit duplicate detection and maximality test with a collection of already discovered patterns. ◦ This requires large memory and delay time by these approaches, and introduces difficulties to use efficient search techniques, e. g. , depth-first search. �Open problem: output-polynomial time computability of the maximal pattern problem for the class of geometric graphs.

Related works: Graph mining �Frequent subgraph mining: ◦ AGM [Inokuchi, Washio, Motoda, PKDD’ 00] ◦ Tree. Miner [Zaki, KDD’ 02] ◦ Freqt [Asai et al. , SDM’ 02] ◦ NK [Nijssen & Kok, MGTS’ 03] � Maximal/closed ◦ ◦ subgraph mining Close. Graph [Yan & Han, KDD’ 03] CMTree. Miner [Chi, Yang, Xia, Muntz, PAKDD’ 04] Dryade [Termier, Rousset, Sebag, ICDM’ 04] Clo. Att [Arimura & Uno, ILP’ 05] � Combination with machine learning ◦ XRule [Zaki & Aggrawal, KDD’ 03] ◦ Weighted Substructure Mining [Tsuda & Kudo, ICML’ 06]

Related works: Maximal/Closed pattern mining � 1. The first: Flexible Patterns ◦ Classes of “elastic” or “flexible” patterns ◦ Polynojmial delay and space algoarithms are developed using a very simple “reverse search property” holds ◦ CMTree. Miner [Chi et al. PAKDD’ 04], BIDE [Yan & Han. ICDE’ 04], and Max. Flex [Arimura & Uno, LLLL’ 07] � The second: Rigid patterns ◦ deal with mining of “rigid” patterns which have ◦ Polynojmial delay and space algoarithms based on the existence of least generalization or closure-like operations. ◦ LCM [Uno et al. FIMI’ 03, ’ 04, DS’ 04] proposes ppc-extension for maximal sets, and then Clo. ATT [Arimura & Uno ILP’ 05] and Max. Motif [Arimura & Uno ISAAC’ 05] � The third: others ◦ Heuristic algorithms ◦ Close. Graph [25]: frequent pattern discovery augmented with maximality test and the duplicate detection ◦ Difficult to achieve output-polynomial time computability

Def: Enumeration Algorithms �Efficient data mining algorithm = output-polynomial time algorithms

Algorithm Max. Geo �A time and space efficient algorithm for mining all maximal geometric subgraphs Depth-first search over the space of all maximal geometric subgraphs ◦ To do this. . . �Achieves first time polynomial delay and polynomial space

We develop techniques. . . �A polynomial time computable canonical code for all geometric graphs which is invariant under geometric transformations. �Characterization of M by the intersection operation (the least generalization) and then Polytime computable closure operation for geographs �The tree-shaped search route T for all maximal patterns in G �A new pattern growth technique combining reverse search and closure extension

Main result �Theorem: ◦ Given an input geometric graph D, algorithm Max. Geo enumerates all frequent maximal pattern P in M without duplicates in O(m(m+n)||D||2 log ||D||) = O(n 8 log n) time per pattern and in O(m) = O(n 2) space, ◦ with the maximum number m of occurrences of a pattern other than trivial patterns, the number n of vertices in D, and the number ||D|| of vertices and edges in D. �Corollary: ◦ The maximal pattern enumeration problem is solvable in polynomial delay and polynomial space in the total input size.

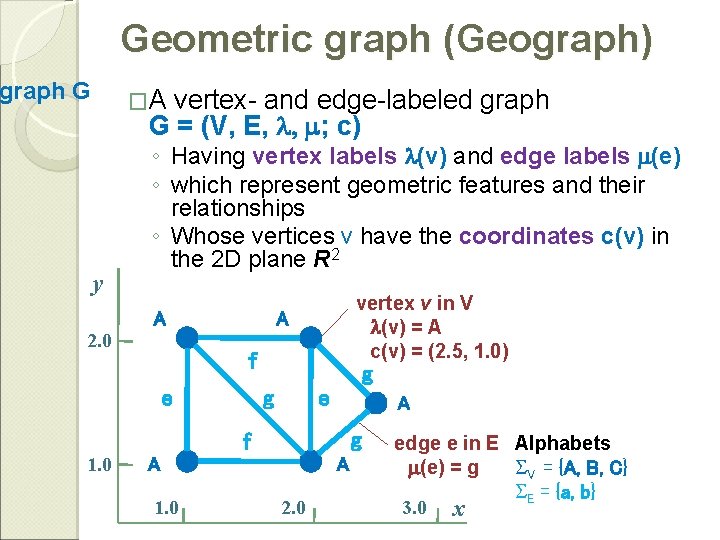
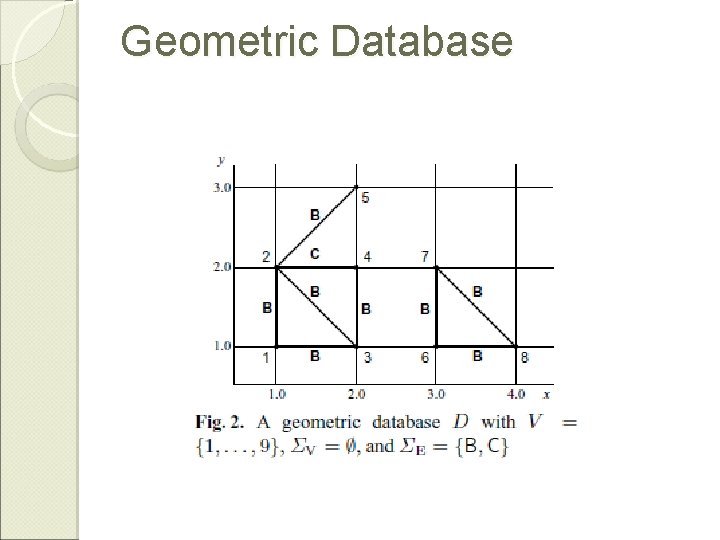
Geometric graph (Geograph) graph G �A vertex- and edge-labeled graph G = (V, E, l, m; c) y ◦ Having vertex labels l(v) and edge labels m(e) ◦ which represent geometric features and their relationships ◦ Whose vertices v have the coordinates c(v) in the 2 D plane R 2 A 2. 0 vertex v in V l(v) = A c(v) = (2. 5, 1. 0) A f e g g e A g f 1. 0 A 2. 0 edge e in E Alphabets m(e) = g SV = {A, B, C} SE = {a, b} 3. 0 x

Basics in Geometry � R 2 : 2 -dim Euclidean space ◦ The set R 2 of all points p = (x, y) (x, y : real numbers) �||x|| : the norm of a vector x �||x - y|| : the distance of x and y �c x : a scalar product �x + y : the addition of vectors �Ax : the product of matrix A and a 2 -vector x �det(A) : the determinant of matrix A �A-1 : the inverse of matrix A �f : R 2 : a geometric transformations �f(x) = Ax + b : an affine transformation

Geometric Isomorphism � Geograph P is geometrically isomorphic to Q iff there exists some F in Tgeo such that T(P) = Q � Class Tgeo of Geometric Transformations: Any combinations F of : ◦ Translation M ◦ Rotation R ◦ Scaling S

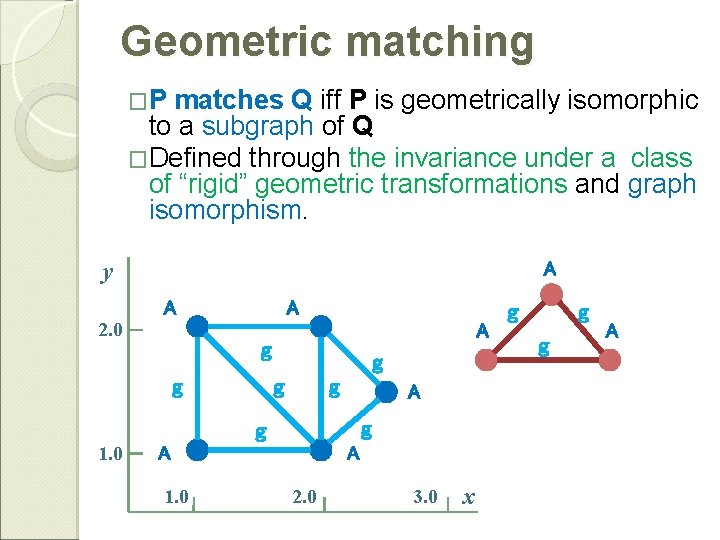
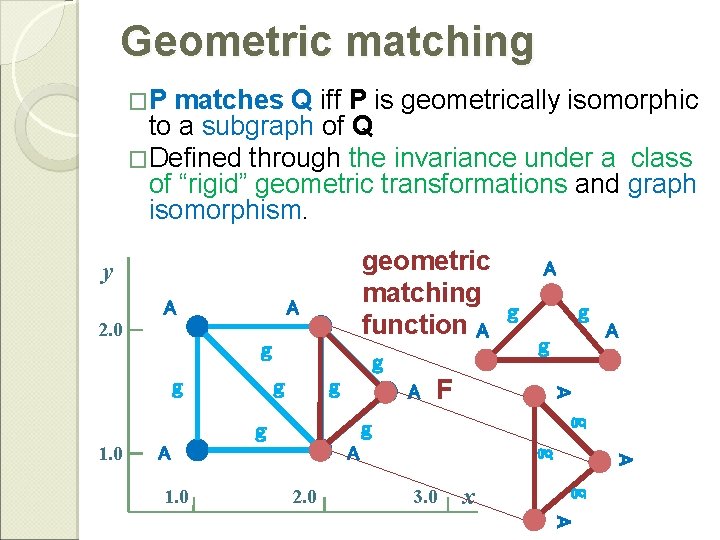
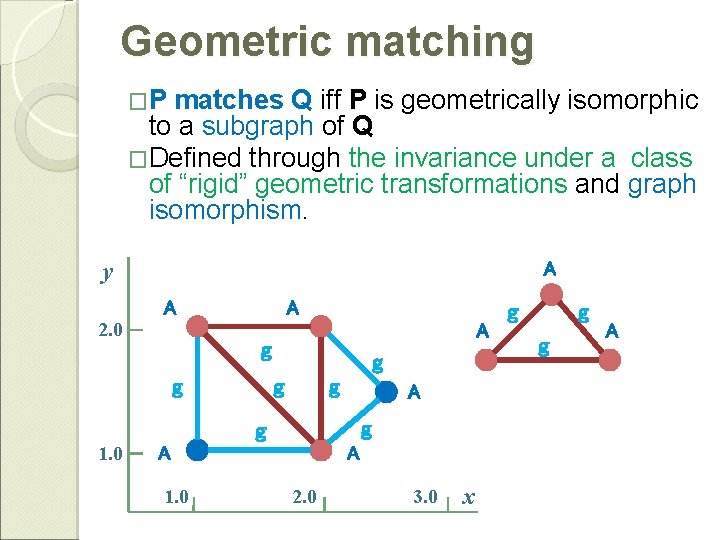
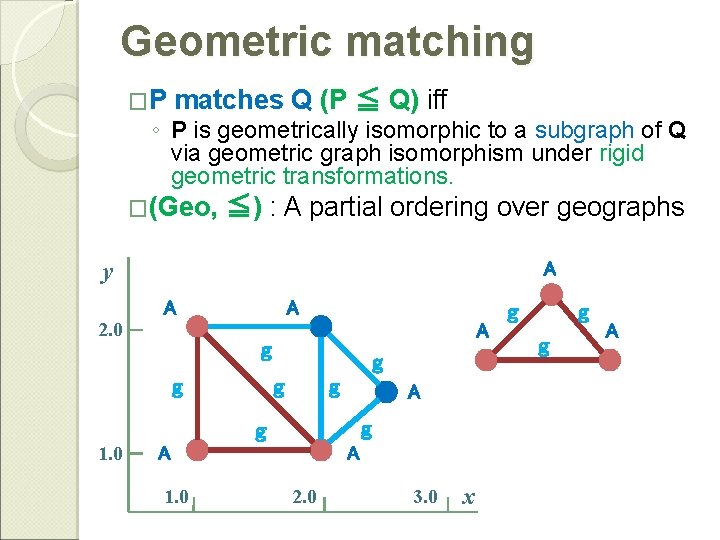
Geometric matching �P matches Q iff P is geometrically isomorphic to a subgraph of Q �Defined through the invariance under a class of “rigid” geometric transformations and graph isomorphism. geometric matching g function A y A 2. 0 A g g g A x A 3. 0 g 2. 0 A g A 1. 0 g g g 1. 0 F g A g g A A

Geometric matching �P matches Q iff P is geometrically isomorphic to a subgraph of Q �Defined through the invariance under a class of “rigid” geometric transformations and graph isomorphism. y A A 2. 0 A A g g g A g g 1. 0 A 2. 0 3. 0 x g g g A

Geometric matching �P matches Q (P ≦ Q) iff ◦ P is geometrically isomorphic to a subgraph of Q via geometric graph isomorphism under rigid geometric transformations. �(Geo, ≦) : A partial ordering over geographs y A A 2. 0 A A g g g A g g 1. 0 A 2. 0 3. 0 x g g g A

Geometric Database

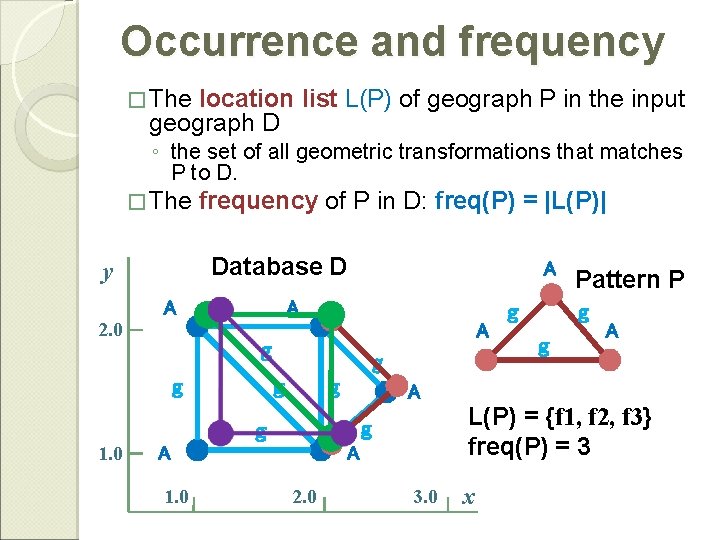
Occurrence and frequency � The location list L(P) of geograph P in the input geograph D ◦ the set of all geometric transformations that matches P to D. � The frequency of P in D: freq(P) = |L(P)| Database D y A 2. 0 A A g g g 1. 0 A 2. 0 g A L(P) = {f 1, f 2, f 3} freq(P) = 3 g A g Pattern P g A g 1. 0 A 3. 0 x

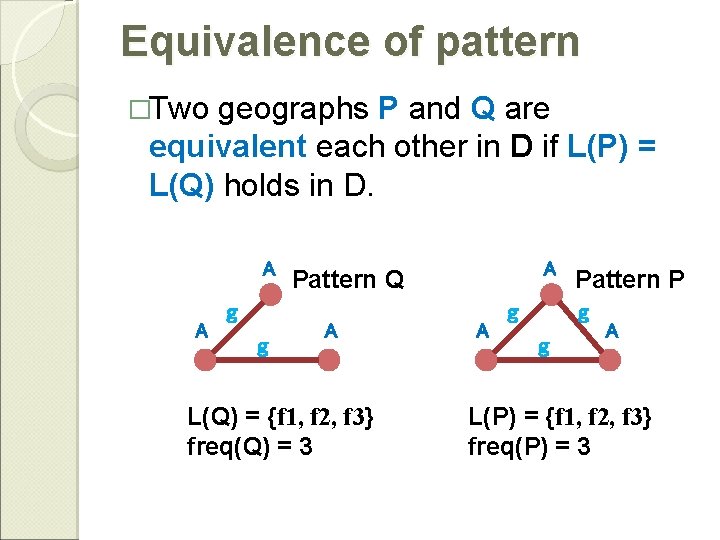
Equivalence of pattern �Two geographs P and Q are equivalent each other in D if L(P) = L(Q) holds in D. A A g g A Pattern Q A L(Q) = {f 1, f 2, f 3} freq(Q) = 3 A g g Pattern P g A L(P) = {f 1, f 2, f 3} freq(P) = 3

Maximal patterns �A maximal pattern ◦ A geometric graph which is not included in any properly larger subgraph w. r. t. ≦ having the same set of occurrences in D. ◦ A maximal element within the equivalence class of geographs w. r. t. location list equivalence. �Lemma 1 (unique maximal pattern) For any geometric pattern P, there exists the unique maximal pattern equivalent to P �Proof: Take the intersection of all geographs in the equivalence class [P] = { Q in Geo : L(P) = L(Q) in D }. This is the

Maximal pattern mining �A maximal pattern ◦ is a geometric graph which is not included in any properly larger subgraph having the same set of occurrences in D. �The maximal subgraph mining problem ◦ asks to find all maximal patterns (closed patterns) appearing in a given input geometric graph D without repetition �The set M of all maximal patterns ◦ is expected to be much smaller than the set F of all frequent patterns and still contains the complete information of D 要修正！

Canonical form �Given a geograph P of size k �Define the canonical code Cano(P) of P as the lexicographically smallest code C(P, N) for all numbering N, where �C(P, N) is defined as follows ◦ Determine a numbering N of all the vertices of P in 1, 2, 3, . . . , k ◦ Sort the collection of all labeled verticies and labeled edges: �(c(v), l(v) for all v in V �(c(u), c(v), m(u, v)) for all edges e = (u, v) in E 要修正！ ◦ Let C(P, N) be the resulting list as the code by N

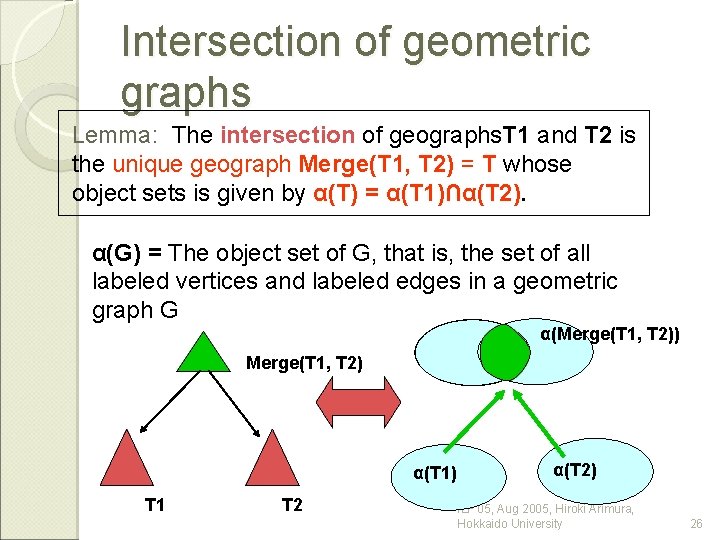
Intersection of geometric graphs Lemma: The intersection of geographs. T 1 and T 2 is the unique geograph Merge(T 1, T 2) = T whose object sets is given by α(T) = α(T 1)∩α(T 2). α(G) = The object set of G, that is, the set of all labeled vertices and labeled edges in a geometric graph G α(Merge(T 1, T 2)) Merge(T 1, T 2) α(T 1) T 1 T 2 α(T 2) ILP'05, Aug 2005, Hiroki Arimura, Hokkaido University 26

Closure of geograph �The intersection Merge(P 1, P 2) of a pair of geographs P 1 and P 2 ◦ The intersection of P 1 and P 2 as the first order (relational) structure �The closure of geograph P ◦ Closure(P) = Merge(L(P)) �Theorem: ◦ P is maximal in D iff CLosure(P) = P 要修正！

Tree-shaped search route for maximal patterns �The core of (the code of) a geograph P ◦ The shortest prefix core(P) of code(P) such that L(P) = L(core(P)) �The parent P of maximal geograph Q ◦ Parent(P) = Closure(the proper prefix of core(the code of P)) �Theorem: 要修正！ The graph Tree(Geo) = (Geo, Parent(. )) forms a spanning tree for Geo with the empty geograph as

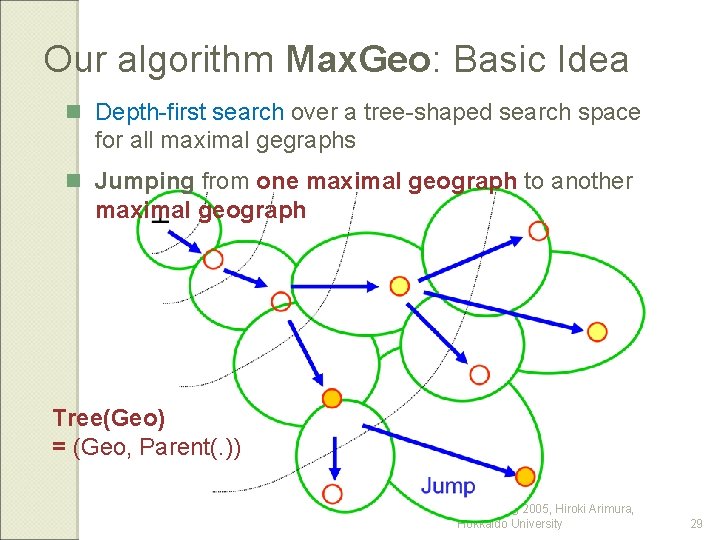
Our algorithm Max. Geo: Basic Idea n Depth-first search over a tree-shaped search space for all maximal gegraphs n Jumping from one maximal geograph to another maximal geograph Tree(Geo) = (Geo, Parent(. )) ILP'05, Aug 2005, Hiroki Arimura, Hokkaido University 29

Main result �Theorem: ◦ Given an input geometric graph D, algorithm Max. Geo enumerates all frequent maximal pattern P in M without duplicates in O(m(m+n)||D||2 log ||D||) = O(n 8 log n) time per pattern and in O(m) = O(n 2) space, ◦ with the maximum number m of occurrences of a pattern other than trivial patterns, the number n of vertices in D, and the number ||D|| of vertices and edges in D. �Corollary: ◦ The maximal pattern enumeration problem is solvable in polynomial delay and polynomial space in the total input size.

Summary: We develop techniques. . . �A polynomial time computable canonical code for all geometric graphs which is invariant under geometric transformations. �Characterization of M by the intersection operation (the least generalization) and then Polytime computable closure operation for geographs �The tree-shaped search route T for all maximal patterns in G �A new pattern growth technique combining reverse search and closure extension

Conclusion �The class of geometric graphs �Maximal pattern discovery problem �A polynomial space and polynomial delay algorithm Max. Geo �Time and space complexity �Techniques