Efficient Inference in Fully Connected CRFs with Gaussian

Efficient Inference in Fully Connected CRFs with Gaussian Edge Potentials by Phillip Krahenbuhl and Vladlen Koltun NIPS 2011 (oral, best student paper) Presented by HAO-WEI, YEH 2014/11/06

Outline CRF Brief Intro. of MRF vs. CRF About the paper Goal : Multi-class image segmentation Speedup the inference for complex CRF Model Definition Inference Mean Field Approximation Efficient message passing using high-dimensional filtering Learning Results

CRF

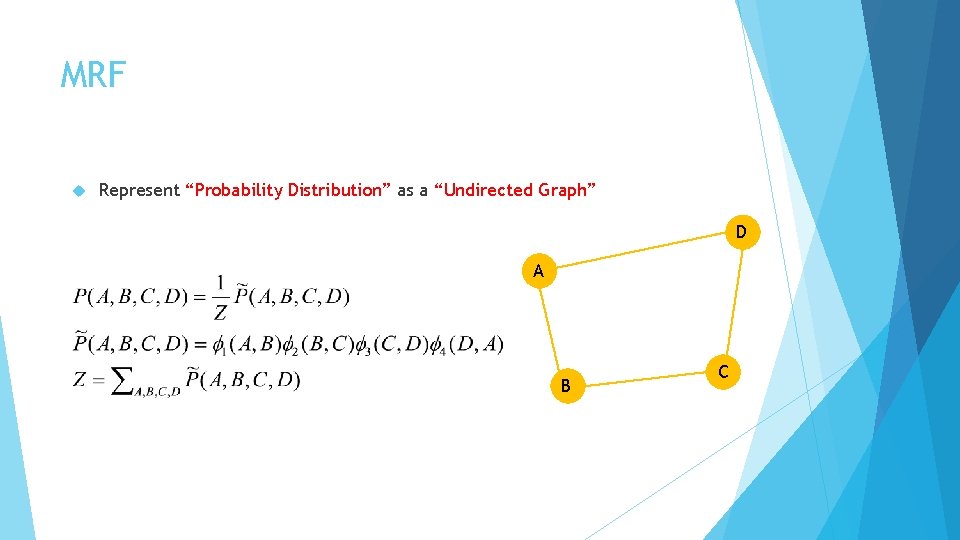
MRF Represent “Probability Distribution” as a “Undirected Graph” D A B C

CRF vs. MRF For MAP inference :

About the paper

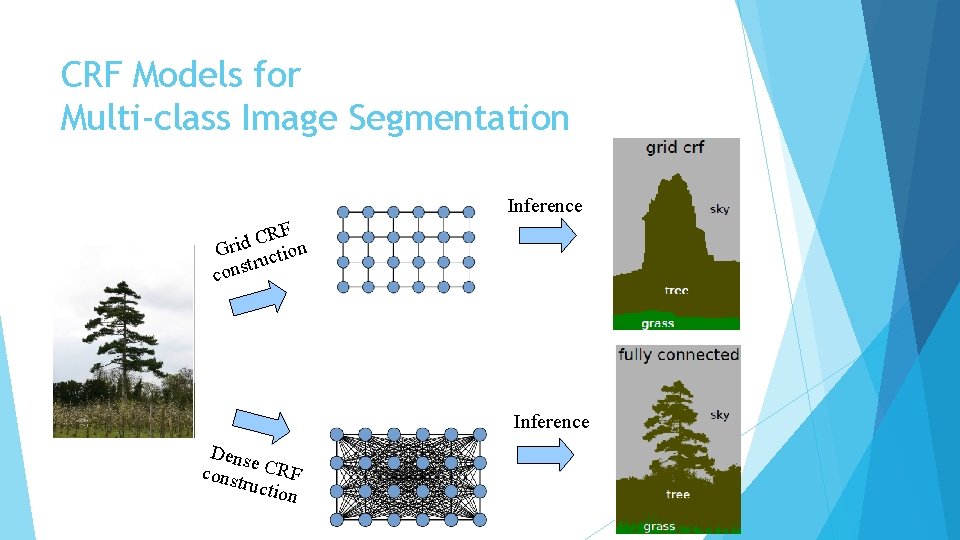
Multi-class Image Segmentation

CRF Models for Multi-class Image Segmentation Inference RF C d i Gr uction tr cons Inference Dens e const CRF ructio n

Adjacency CRF Models MAP inference in conditional random field Unary term From classifier Pairwise term Consistent labeling Neighboring pixels Color-sensitive Potts model

Adjacency CRF Models Efficient inference 1 second for 500000 variables Limited expressive power Only local interactions Excessive smoothing of object boundaries Shrinking bias

Fully Connected CRF MAP inference in conditional random field Unary term From classifier Pairwise term Every node is connected to every other Connections weighted differently

Fully Connected CRF Long-range interactions No more shrinking bias But… Computationally Expensive Region-based [Rabinovich et al. 07, Galleguillos et al. 08, Toyoda & Hasegawa 08, Payet & Todorovic 10] Tractable up to hundreds of variables Limited by the unsupervised segmentation producing the regions Pixel-based Tens of thousands of variables Billions of edges Computationally expensive Main contribution of the paper!!

Model Definition K=2 Label compatibility Potts model: Semi-metric model: Appearance kernel Color-sensitive model Local smoothness Discourages pixel level noise learned from data

Inference – Mean Field Approximation MAP But P(x) is too difficult to find… Mean Field Approximation

Inference – Mean Field Approximation Bottleneck!!

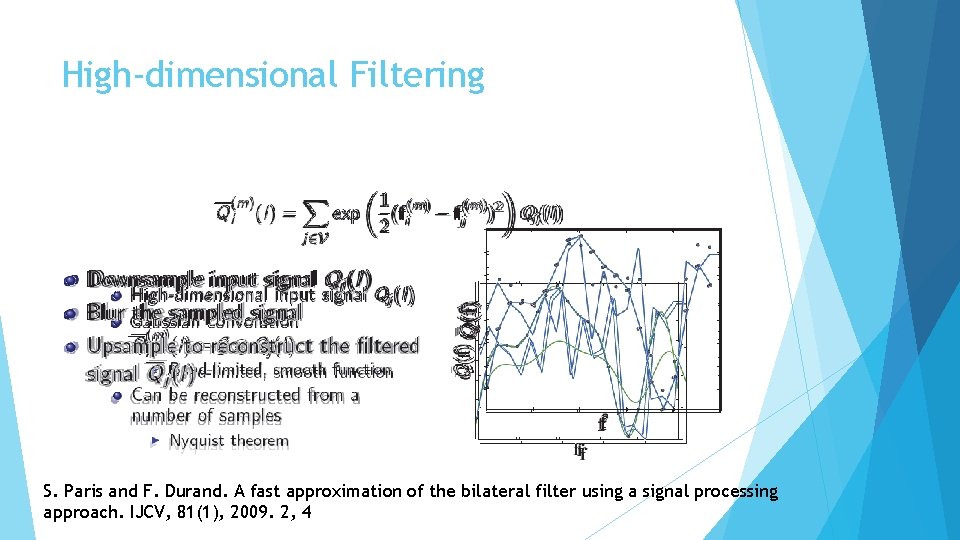
High-dimensional Filtering S. Paris and F. Durand. A fast approximation of the bilateral filter using a signal processing approach. IJCV, 81(1), 2009. 2, 4

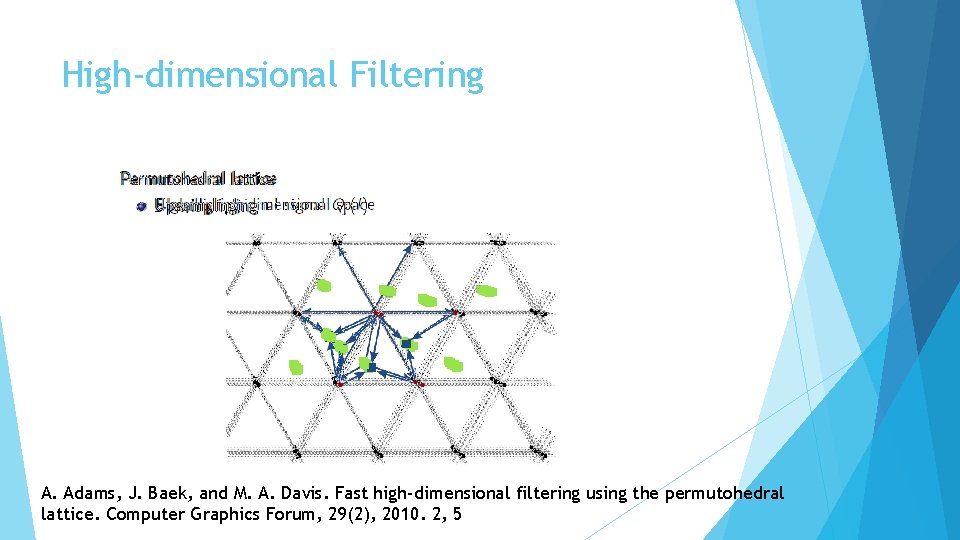
High-dimensional Filtering A. Adams, J. Baek, and M. A. Davis. Fast high-dimensional filtering using the permutohedral lattice. Computer Graphics Forum, 29(2), 2010. 2, 5

Inference – Mean Field Approximation Faster!!

Parameters Learning Unary Potentials Texton. Boost [Shotton et al. 09] Kernel Bandwidths are hard to learn W(1), θα, θβ : grid search to pick the best ones W(2) = θγ = 1 : not significantly affect classification accuracy μ(xi, xj) L-BGFS (approximate Newton’s method )

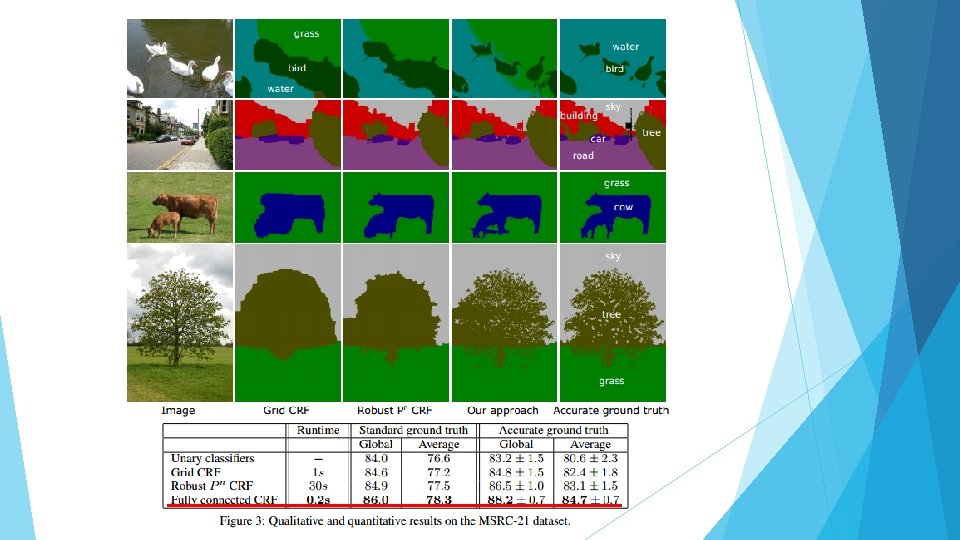
Experiment Results

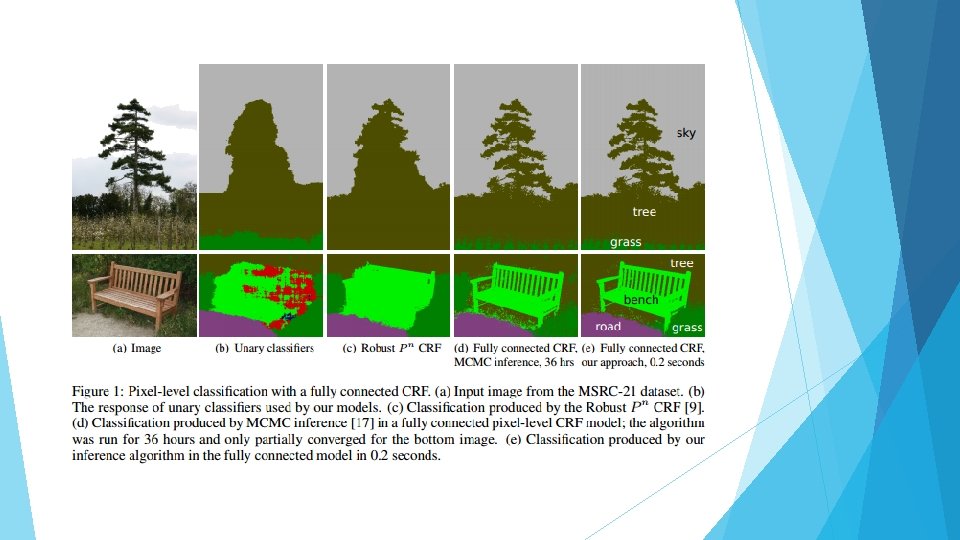
Long Range Connection

Reported Failures

Conclusion About the paper Goal : Multi-class image segmentation Contribution : Speedup the inference for complex CRF

References Paper http: //stanford. edu/~philkr/ http: //graphics. stanford. edu/projects/densecrf/ http: //www. cs. cmu. edu/~efros/courses/LBMV 12/crf_deconstruction. pdf Relative Knowledge Wikipedia http: //jamie. shotton. org/work/publications/ijcv 07 a. pdf http: //blog. sciencenet. cn/blog-284987 -656648. html www. cs. unc. edu/~lazebnik/fall 09/random_fields. pptx http: //www. cs. cmu. edu/~16831 -f 14/notes/F 11/16831_lecture 07_bneuman. pdf http: //blog. csdn. net/itplus/article/details/21897443 http: //graphics. stanford. edu/papers/permutohedral. pdf http: //research. microsoft. com/en-us/um/people/pkohli/papers/klt_CVPR 08. pdf