Efficient Image Search and Retrieval using Compact Binary

Efficient Image Search and Retrieval using Compact Binary Codes Rob Fergus (NYU) Jon Barron (NYU/UC Berkeley) Antonio Torralba (MIT) Yair Weiss (Hebrew U. ) CVPR 2008

Large scale image search Internet contains many billions of images How can we search them, based on visual content? The Challenge: – Need way of measuring similarity between images – Needs to scale to Internet

Current Image Search Engines Essentially text-based

Existing approaches to Content-Based Image Retrieval • Focus of scaling rather than understanding image • Variety of simple/hand-designed cues: – Color and/or Texture histograms, Shape, PCA, etc. • Various distance metrics – Earth Movers Distance (Rubner et al. ‘ 98) • Most recognition approaches slow (~1 sec/image)

Our Approach • Learn the metric from training data • Use compact binary codes for speed DO BOTH TOGETHER

Large scale image/video search • Representation must fit in memory (disk too slow) • Facebook has ~10 billion images (1010) • PC has ~10 Gbytes of memory (1011 bits) Budget of 101 bits/image • You. Tube has ~ a trillion video frames (1012) • Big cluster of PCs has ~10 Tbytes (1014 bits) Budget of 102 bits/frame

Some file sizes • Typical You. Tube clip (compressed) is ~ 108 bits • 1 Megapixel JPEG image is ~ 107 bits • 32 x 32 color image is ~ 104 bits - Smallest useful image size 101 - 102 bits is not much Need a really compact image representation

Binary codes for images • Want images with similar content to have similar binary codes • Use Hamming distance between codes – Number of bit flips – E. g. : Ham_Dist(10001010, 10001110)=1 Ham_Dist(10001010, 1110)=3 • Semantic Hashing [Salakhutdinov & Hinton, 2007] – Text documents

Semantic Hashing [Salakhutdinov & Hinton, 2007] for text documents Query Image Semantic Hash Function Quite different to a (conventional) randomizing hash Binary code Semantically similar images Address Space Images in database Query address

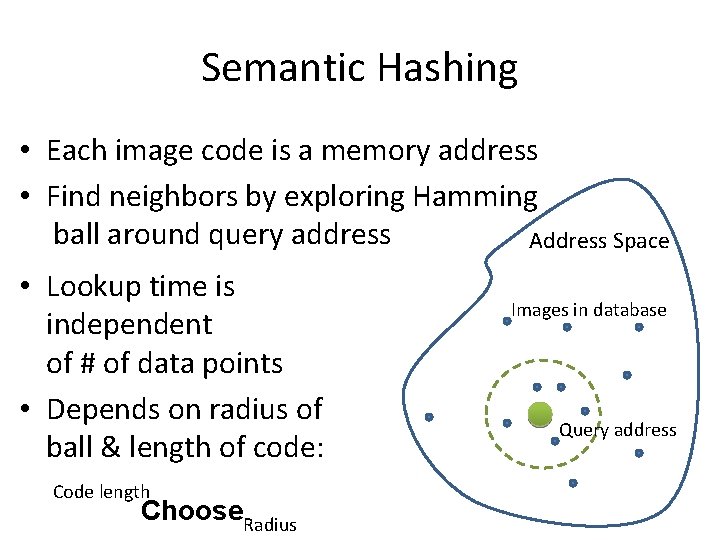
Semantic Hashing • Each image code is a memory address • Find neighbors by exploring Hamming ball around query address Address Space • Lookup time is independent of # of data points • Depends on radius of ball & length of code: Code length Choose. Radius Images in database Query address

Code requirements • • Similar images Similar Codes Very compact (<102 bits/image) Fast to compute Does NOT have to reconstruct image Three approaches: 1. Locality Sensitive Hashing (LSH) 2. Boosting 3. Restricted Boltzmann Machines (RBM’s)

Input Image representation: Gist vectors • • Pixels not a convenient representation Use Gist descriptor instead (Oliva & Torralba, 2001) 512 dimensions/image (real-valued 16, 384 bits) L 2 distance btw. Gist vectors not bad substitute for human perceptual distance NO COLOR INFORMATION Oliva & Torralba, IJCV 2001

1. Locality Sensitive Hashing • Gionis, A. & Indyk, P. & Motwani, R. (1999) • Take random projections of data • Quantize each projection with few bits 101 0 Gist descriptor 1 0 1 1 0 No learning involved

2. Boosting • Modified form of Boost. SSC [Shaknarovich, Viola & Darrell, 2003] • Positive examples are pairs of similar images • Negative examples are pairs of unrelated images 0 0 1 1 0 1 Learn threshold & dimension for each bit (weak classifier)

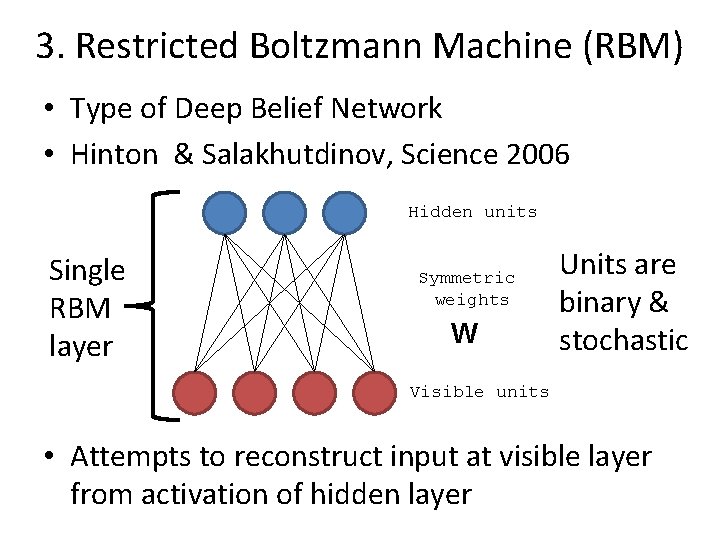
3. Restricted Boltzmann Machine (RBM) • Type of Deep Belief Network • Hinton & Salakhutdinov, Science 2006 Hidden units Single RBM layer Symmetric weights W Units are binary & stochastic Visible units • Attempts to reconstruct input at visible layer from activation of hidden layer

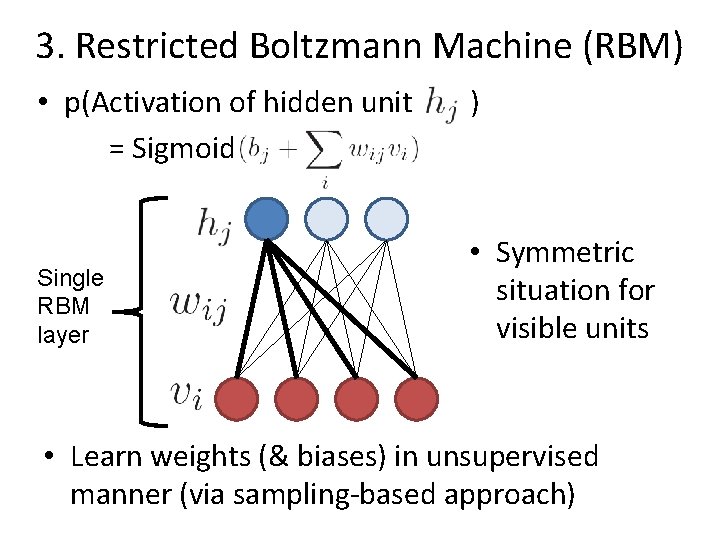
3. Restricted Boltzmann Machine (RBM) • p(Activation of hidden unit = Sigmoid ) Single RBM layer ) • Symmetric situation for visible units • Learn weights (& biases) in unsupervised manner (via sampling-based approach)

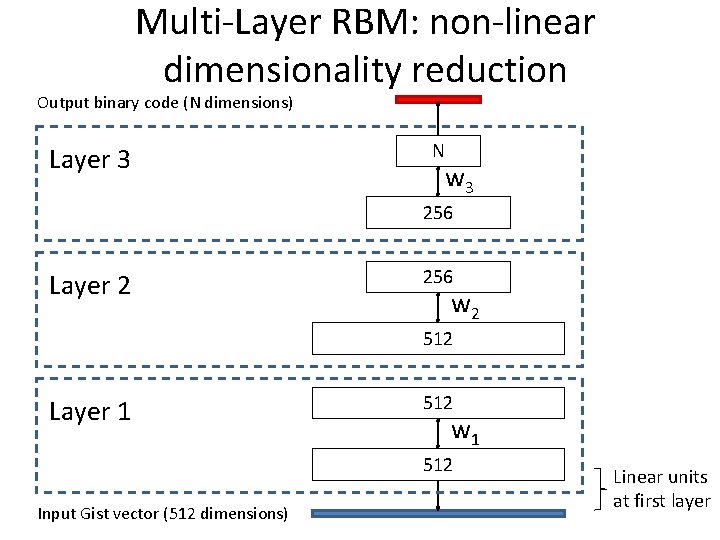
Multi-Layer RBM: non-linear dimensionality reduction Output binary code (N dimensions) Layer 3 N w 3 256 Layer 2 256 w 2 512 Layer 1 512 w 1 512 Input Gist vector (512 dimensions) Linear units at first layer

Training RBM models 1 st Phase: Pre-training 2 nd Phase: Fine-tuning Unsupervised Supervised Can use unlabeled data (unlimited quantity) Requires labeled data (limited quantity) Learn parameters greedily per layer Back propagate gradients of chosen error function Gets them to right ballpark Moves parameters to local minimum

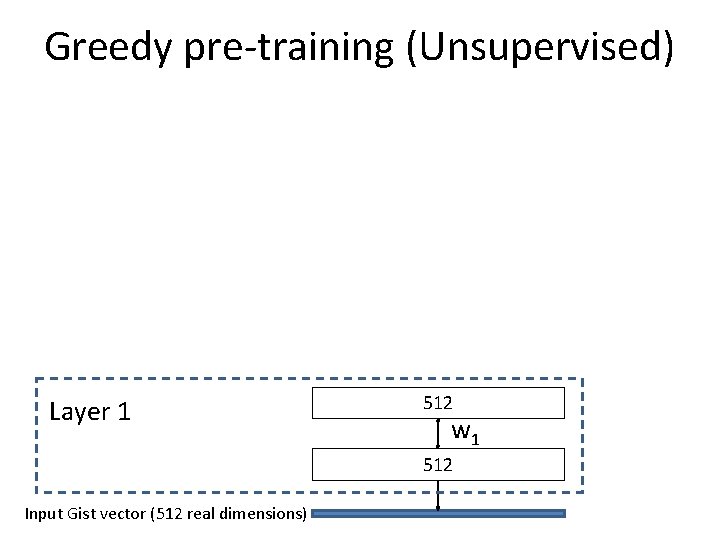
Greedy pre-training (Unsupervised) Layer 1 512 w 1 512 Input Gist vector (512 real dimensions)

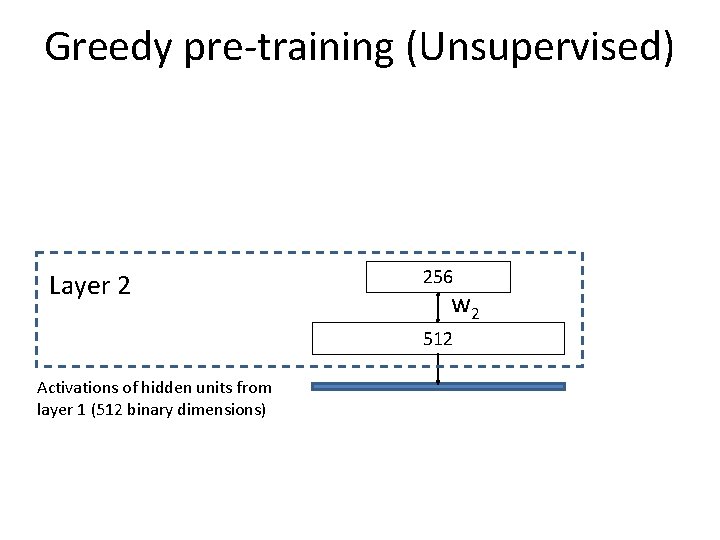
Greedy pre-training (Unsupervised) Layer 2 256 w 2 512 Activations of hidden units from layer 1 (512 binary dimensions)

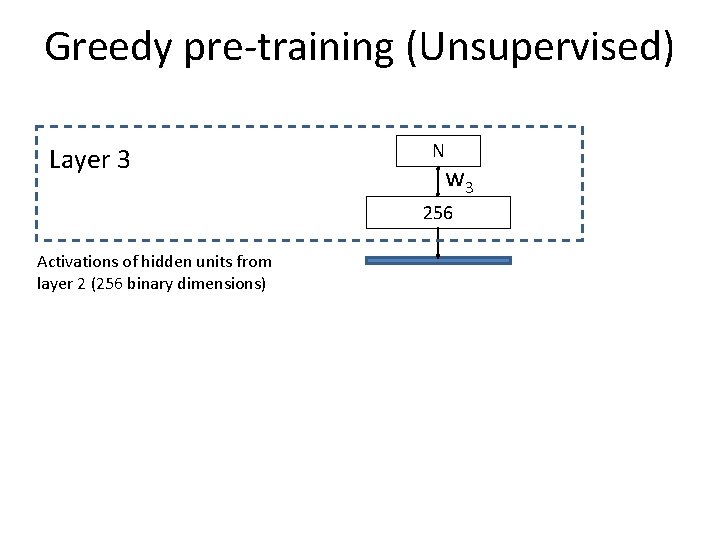
Greedy pre-training (Unsupervised) Layer 3 N w 3 256 Activations of hidden units from layer 2 (256 binary dimensions)

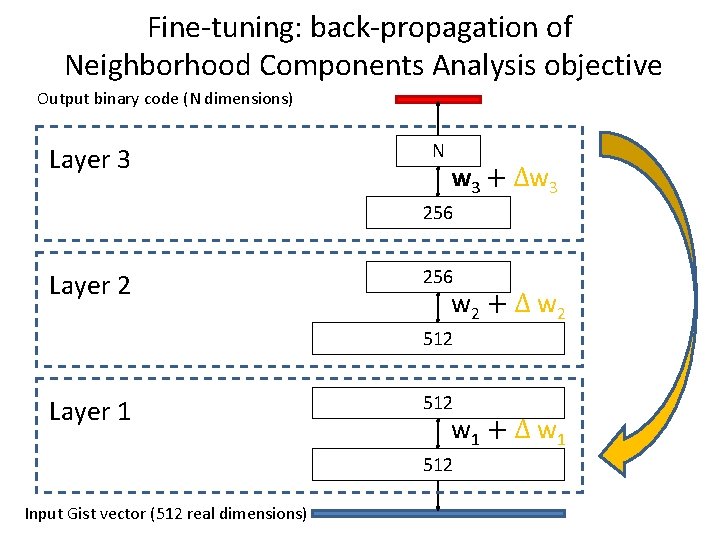
Fine-tuning: back-propagation of Neighborhood Components Analysis objective Output binary code (N dimensions) Layer 3 N w 3 + ∆w 3 256 Layer 2 256 w 2 + ∆ w 2 512 Layer 1 512 w 1 + ∆ w 1 512 Input Gist vector (512 real dimensions)

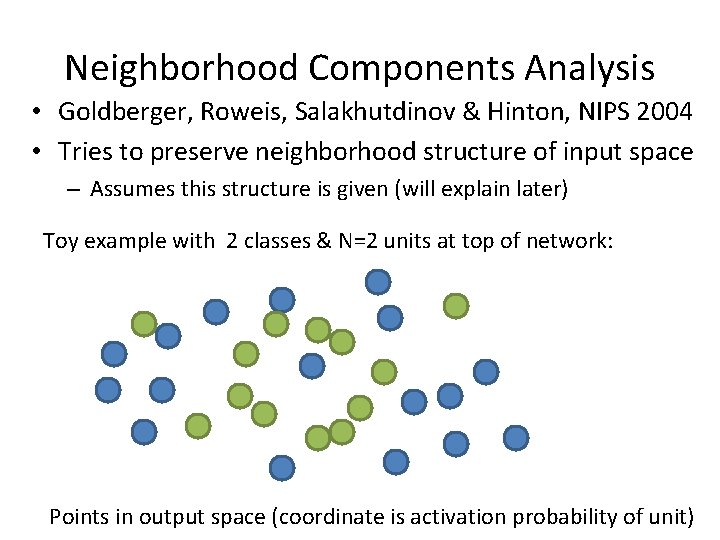
Neighborhood Components Analysis • Goldberger, Roweis, Salakhutdinov & Hinton, NIPS 2004 • Tries to preserve neighborhood structure of input space – Assumes this structure is given (will explain later) Toy example with 2 classes & N=2 units at top of network: Points in output space (coordinate is activation probability of unit)

Neighborhood Components Analysis • Adjust network parameters (weights and biases) to move: – Points of SAME class closer – Points of DIFFERENT class away

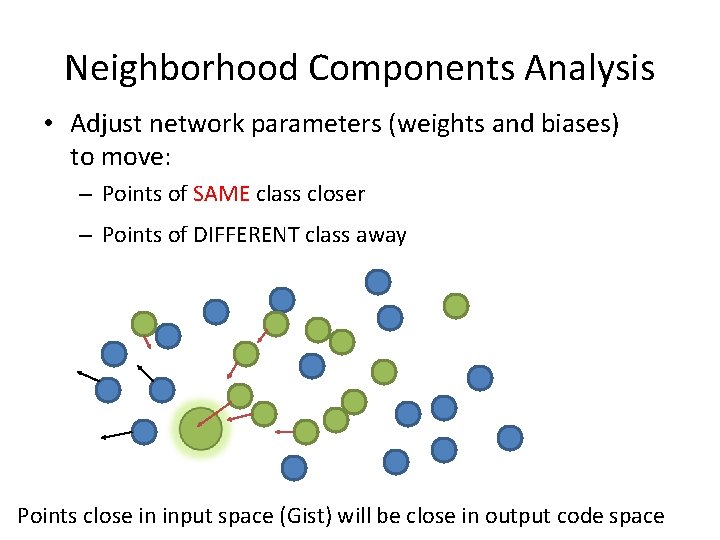
Neighborhood Components Analysis • Adjust network parameters (weights and biases) to move: – Points of SAME class closer – Points of DIFFERENT class away Points close in input space (Gist) will be close in output code space

Simple Binarization Strategy Set threshold - e. g. use median 0 1

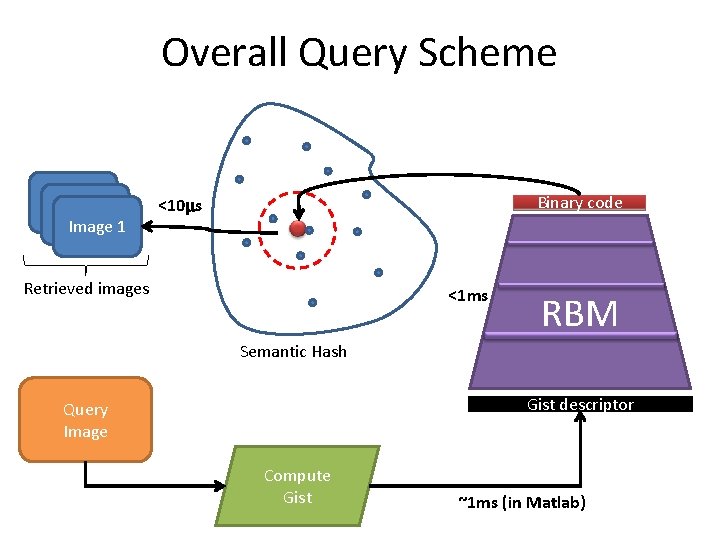
Overall Query Scheme Image 1 Binary code <10μs Retrieved images <1 ms RBM Semantic Hash Gist descriptor Query Image Compute Gist ~1 ms (in Matlab)

Retrieval Experiments

Test set 1: Label. Me • 22, 000 images (20, 000 train | 2, 000 test) • Ground truth segmentations for all • Can define ground truth distance btw. images using these segmentations

Defining ground truth • Boosting and NCA back-propagation require ground truth distance between images • Define this using labeled images from Label. Me

Defining ground truth • Pyramid Match (Lazebnik et al. 2006, Grauman & Darrell 2005)

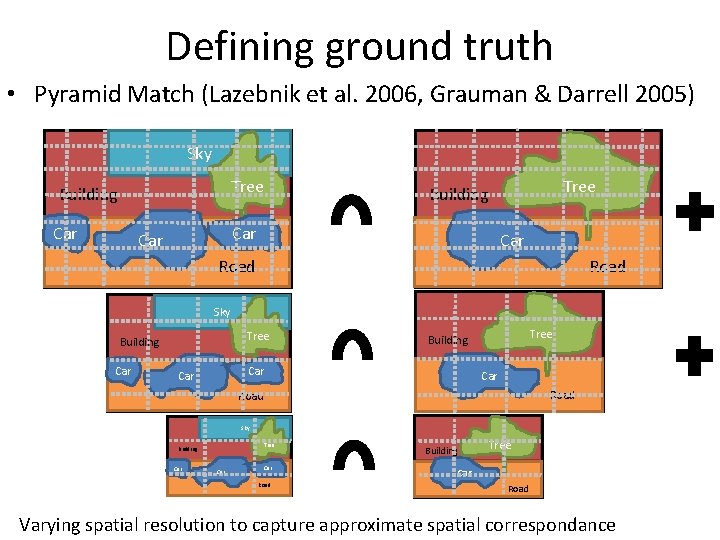
Defining ground truth • Pyramid Match (Lazebnik et al. 2006, Grauman & Darrell 2005) Sky Tree Building Car Car Road Sky Tree Building Car Car Tree Building Car Road Sky Tree Building Car Car Road Building Tree Car Road Varying spatial resolution to capture approximate spatial correspondance

Examples of Label. Me retrieval • 12 closest neighbors under different distance metrics

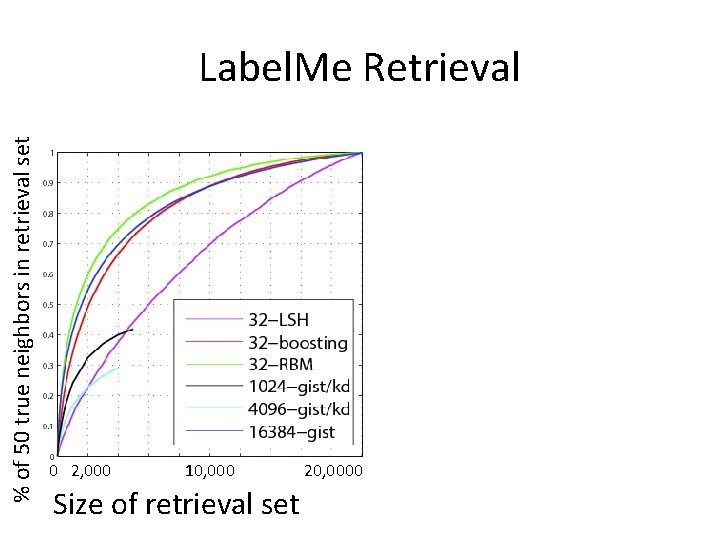
% of 50 true neighbors in retrieval set Label. Me Retrieval 0 2, 000 10, 000 Size of retrieval set 20, 0000

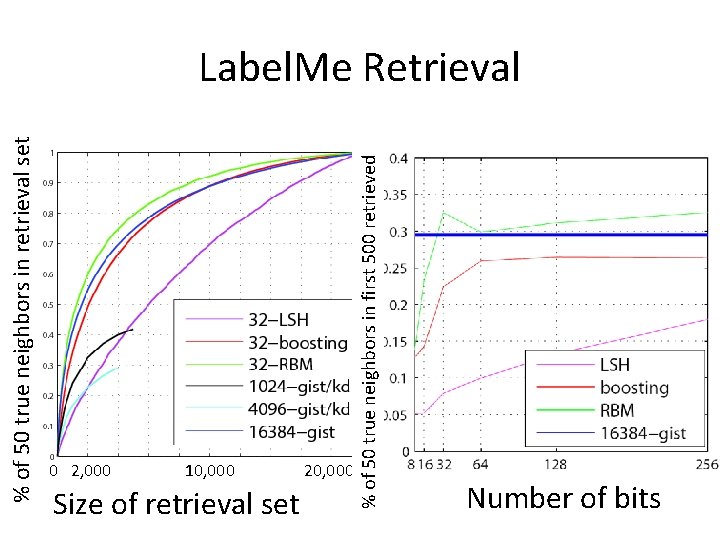
% of 50 true neighbors in retrieval set 0 2, 000 10, 000 Size of retrieval set 20, 0000 % of 50 true neighbors in first 500 retrieved Label. Me Retrieval Number of bits

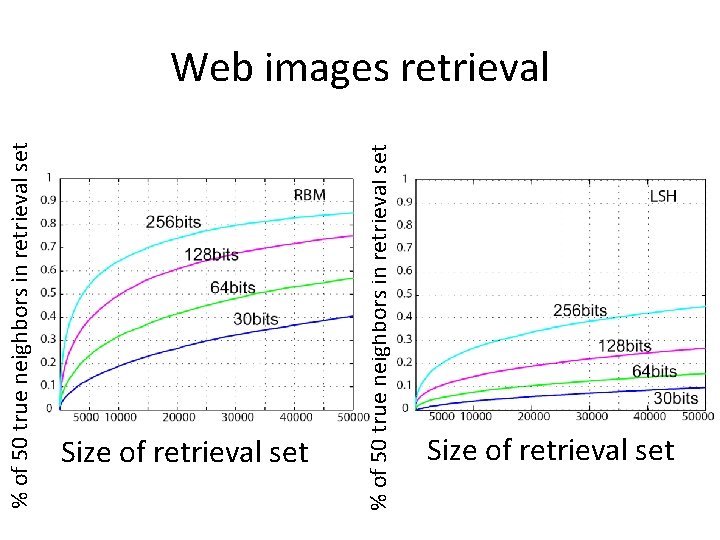
Test set 2: Web images • 12. 9 million images • Collected from Internet • No labels, so use Euclidean distance between Gist vectors as ground truth distance

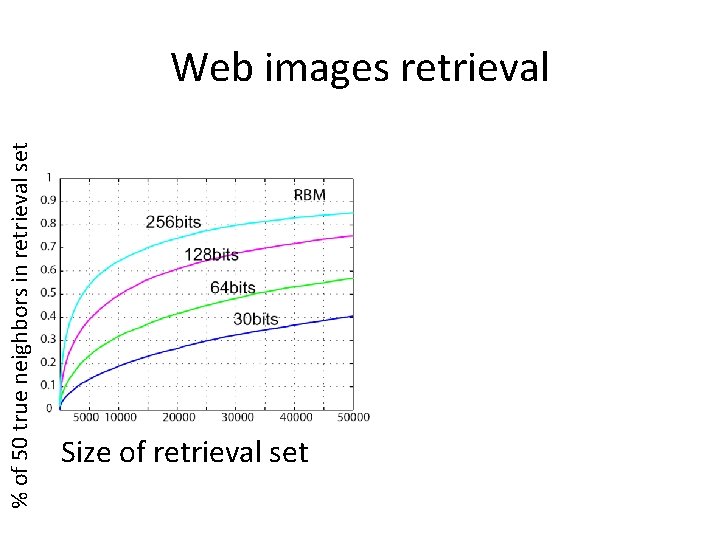
% of 50 true neighbors in retrieval set Web images retrieval Size of retrieval set

% of 50 true neighbors in retrieval set Size of retrieval set % of 50 true neighbors in retrieval set Web images retrieval Size of retrieval set

Examples of Web retrieval • 12 neighbors using different distance metrics

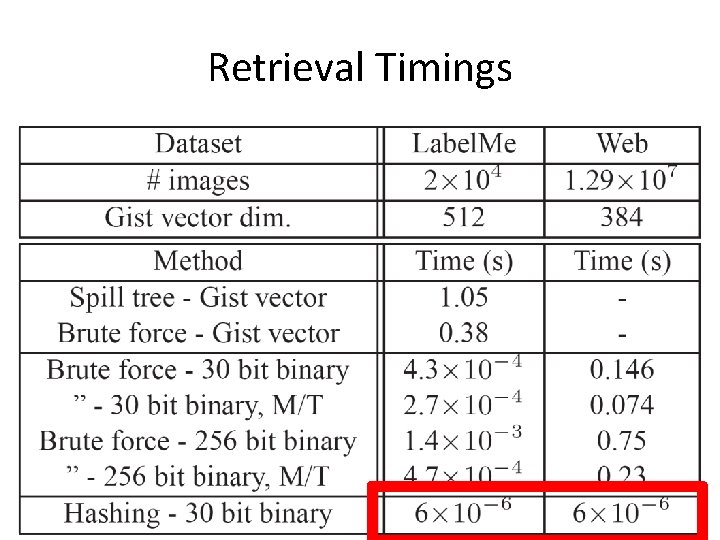
Retrieval Timings

Scaling it up • Google very interested in it • Jon Barron summer internship at Google NYC • NCA has N 2 cost • Use Dr. LIM (Hadsell, Chopra, Le. Cun 2006) • Train on Google proprietary labels

Further Directions 1. Spectral Hashing 2. Brute Force Object Recognition

Spectral Hashing (NIPS ’ 08) • Assume points are embedded in Euclidean space • How to binarize so Hamming distance approximates Euclidean distance? • Under certain (reasonable) assumptions, analytic form exists • No learning, super-simple • Come to Machine Learning seminar on Dec 2 nd ……

2 -D Toy example: 3 bits 7 bits Query Point 15 bits Distance from query point Red – 0 bits Green – 1 bit Black Blue – 2 bits – >2 bits

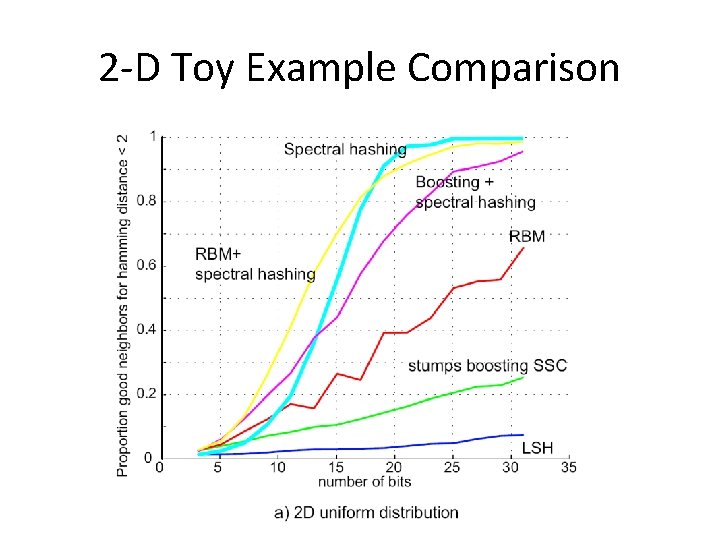
2 -D Toy Example Comparison

Further Directions 1. Spectral Hashing 2. Brute Force Object Recognition

80 Million Tiny Images (PAMI ‘ 08) Implemented by # images 105 106 108

Label. Me Recognition examples

Summary • Explored various approaches to learning binary codes for hashing-based retrieval – Very quick with performance comparable to complex descriptors • Remaining issues: – How to learn metric (so that it scales) – How to produce binary codes – How to use for recognition