Efficient heuristic algorithms for the maximum subarray problem

Efficient heuristic algorithms for the maximum subarray problem Rung-Ren Lin and Kun-Mao Chao

Preview ¡ Trying to guess the answer intelligently. ¡ Preliminary experiments show that these approaches are very promising for locating the maximum subarray in a given twodimensional array.

Review of Maximum Subarray ¡ Bentley posed the maximum subarray problem in his book “Programming Pearls” in 1984. ¡ He introduces Kadane's algorithm for the one -dimensional case, whose time is linear.

Cont’d ¡ Given an m×n array of numbers, Bentley solved the problem in O(m 2 n) time. ¡ An improvement O(m 2 n(loglogm/logm)0. 5) was given by Tamaki et al. in 1998. l This algorithm is heavily recursive and complicated.

Applications 20 25 30 35 40 45 50 55 60 $ $$ $$$$$$ $$$$$$$

Cont’d

Heuristic Methods ¡ Given a 2 -D array A[1. . m][1. . n], let TL[i][j] denote the sum of the rectangle A[1. . i][1. . j]. A TL -3 1 2 -3 -2 0 2 -1 0 -1 -1 1 0 -2 1 -1 -3 0

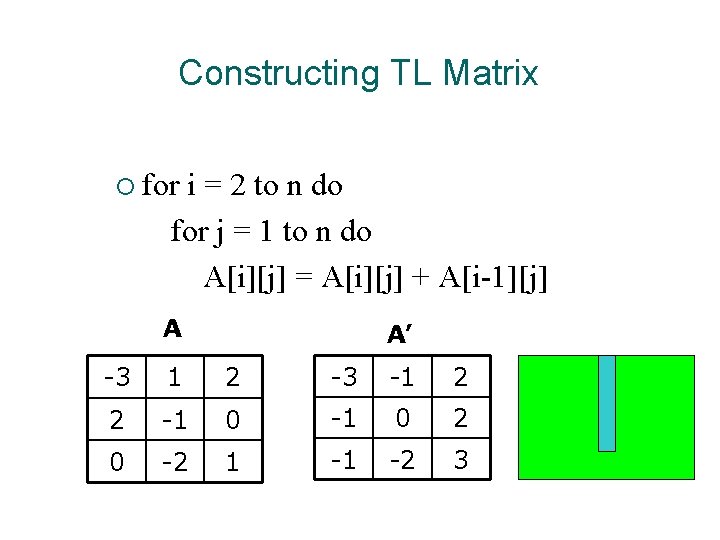
Constructing TL Matrix ¡ for i = 2 to n do for j = 1 to n do A[i][j] = A[i][j] + A[i-1][j] A A’ -3 1 2 -3 -1 2 2 -1 0 2 0 -2 1 -1 -2 3

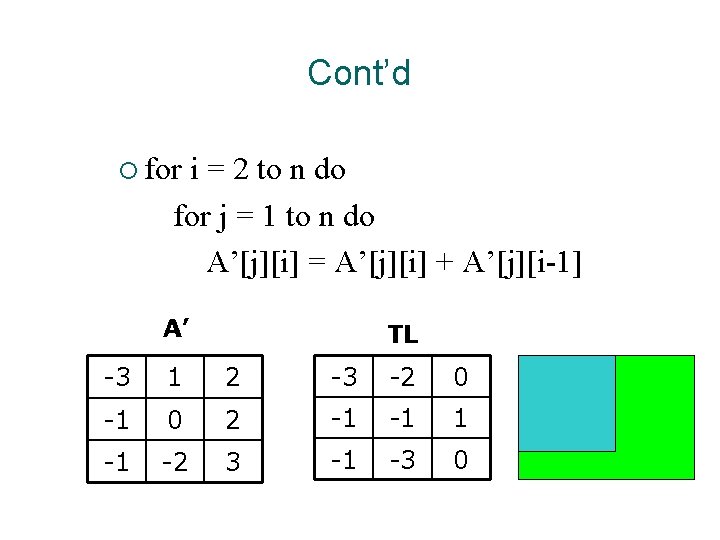
Cont’d ¡ for i = 2 to n do for j = 1 to n do A’[j][i] = A’[j][i] + A’[j][i-1] A’ TL -3 1 2 -3 -2 0 -1 0 2 -1 -1 -2 3 -1 -3 0

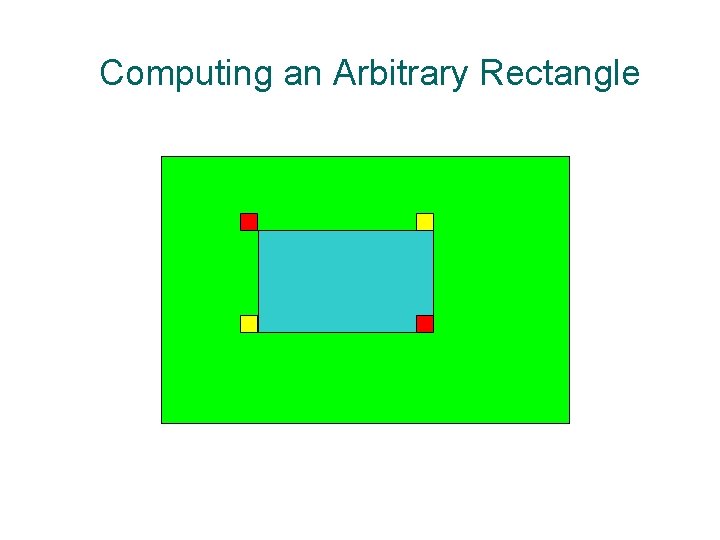
Computing an Arbitrary Rectangle

How to guess？ ¡ Each rectangle can be computed by TL matrix, and the answer is MAX( + - - ). ¡ the larger the better. ¡ the smaller the better.

Cont’d We try only those entries which are in the top k-th, or in the bottom kth for a given k. ¡ We test only O(k) times instead of O(n) times. Since there are in total O(m 2) pairs, this step takes O(km 2). ¡

4 -Corner

Happy New Year!!

Interesting Questions 128 gold. ¡ The way to heaven and hell. ¡ 10 smart prisoners. ¡