Efficient Diversification I Covariance and Portfolio Risk Meanvariance

Efficient Diversification I Covariance and Portfolio Risk Mean-variance Frontier Efficient Portfolio Frontier Investments 9

Some Empirical Evidence In 2000, 40% of stocks in Russell 3000 had returns of -20% or worse. q Meanwhile, less than 12% of U. S. stock mutual funds had returns of -20% or below. q Of the 2, 397 U. S. stocks in existence throughout 1990 s, 22% had negative returns. q In contrast, 0. 4% of U. S. equity mutual funds had negative returns. q Investments 9 2

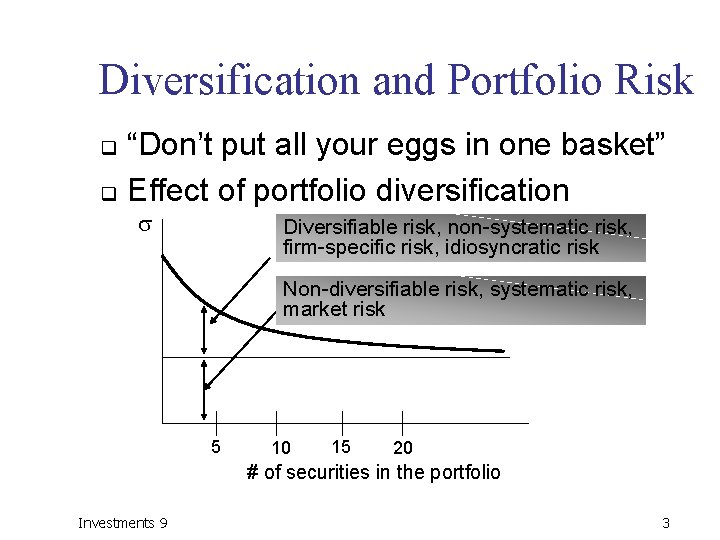
Diversification and Portfolio Risk “Don’t put all your eggs in one basket” q Effect of portfolio diversification q Diversifiable risk, non-systematic risk, firm-specific risk, idiosyncratic risk Non-diversifiable risk, systematic risk, market risk 5 10 15 20 # of securities in the portfolio Investments 9 3

Covariance and Correlation q Covariance and correlation Ø Degree of co-movement of two stocks Covariance: non-standardized measure Ø Correlation coefficient: standardized measure Ø r 2 0< 12 <1 Investments 9 r 1 r 2 -1< 12 <0 r 1 12 =0 4

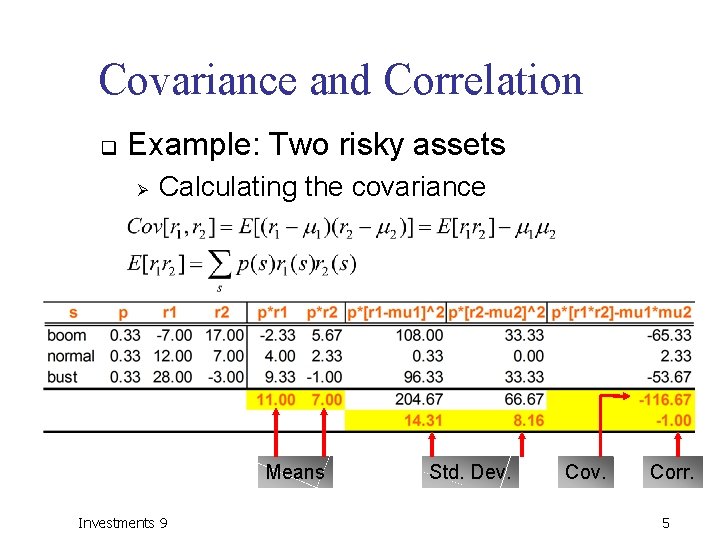
Covariance and Correlation q Example: Two risky assets Ø Calculating the covariance Means Investments 9 Std. Dev. Corr. 5

Diversification and Portfolio Risk q A portfolio of two risky assets Ø Ø w 1: % invested in bond w 2: % invested in stock q Expected return q Variance Investments 9 6

Diversification and Portfolio Risk q Example: Portfolio of two risky securities Ø w in security 1, (1 – w) in security 2 q Expected return (Mean): q Variance q What happens when w changes? Ø Ø Expected return decreases with increasing w How about variance ? . . Investments 9 7

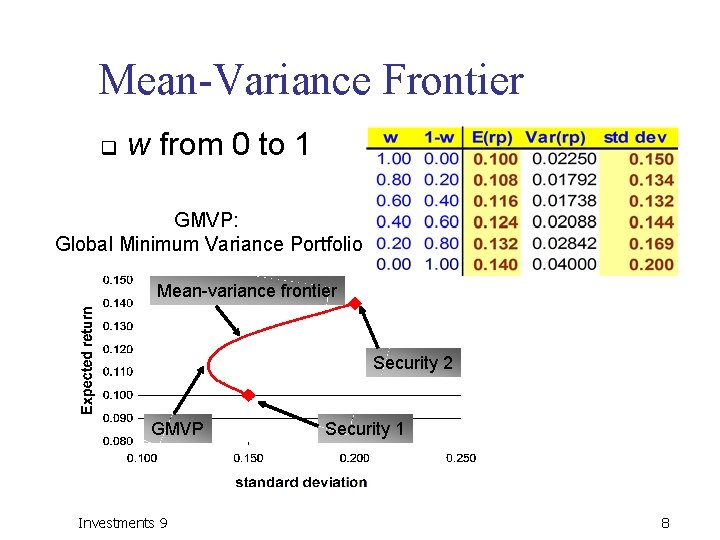
Mean-Variance Frontier q w from 0 to 1 GMVP: Global Minimum Variance Portfolio Mean-variance frontier Security 2 GMVP Investments 9 Security 1 8

Mean-Variance Frontier q Global Minimum Variance Port. (GMVP) Ø A unique w Ø Associated characteristics Investments 9 9

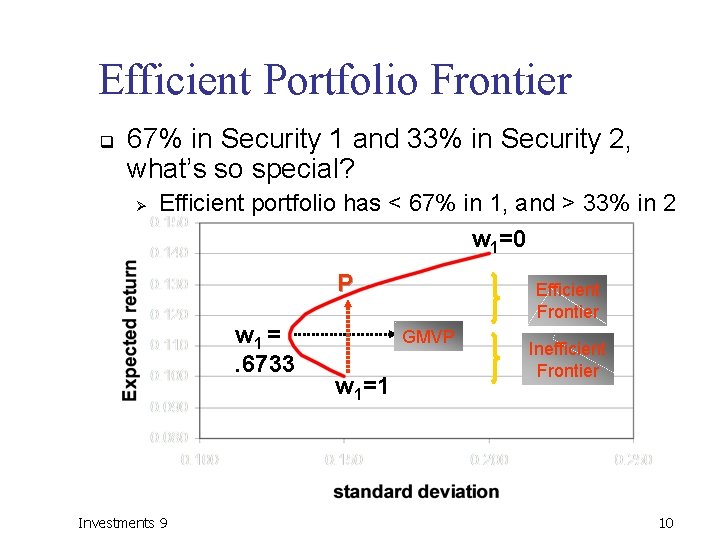
Efficient Portfolio Frontier q 67% in Security 1 and 33% in Security 2, what’s so special? Ø Efficient portfolio has < 67% in 1, and > 33% in 2 w 1=0 P w 1 =. 6733 Investments 9 Efficient Frontier GMVP w 1=1 Inefficient Frontier 10

Efficient Portfolio Frontier q Portfolio “P” dominates Security 1 Ø Ø q The same standard deviation The higher expected return How to find it? Ø Ø Ø Since the portfolio has the same standard deviation as Security 1 Solve the quadratic equation w = 1 (Security 1) or w =. 3465 (Portfolio P) Investments 9 11

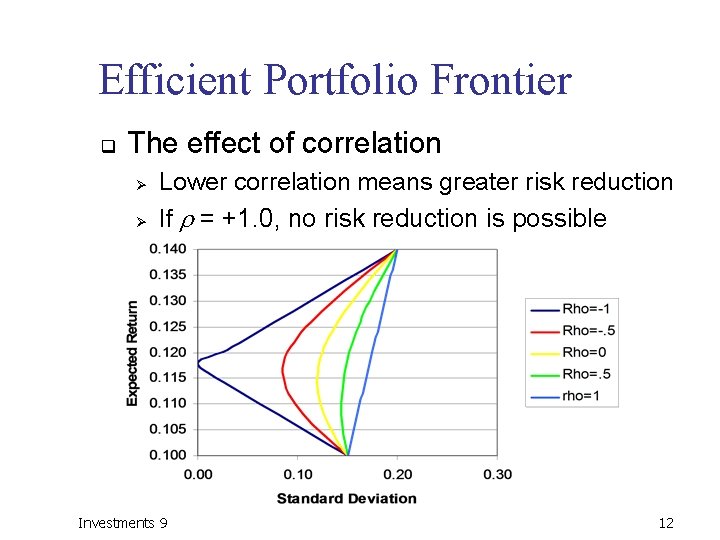
Efficient Portfolio Frontier q The effect of correlation Ø Ø Lower correlation means greater risk reduction If = +1. 0, no risk reduction is possible Investments 9 12

Efficient Portfolio Frontier q Efficient Portfolio of Many securities Ø Ø Ø E[rp]: Weighted average of n securities p 2: Combination of all pair-wise covariance measures Construction of the efficient frontier is complicated q q q Analytical solution without short-sale constraints Numerical solution with short-sale constraints General Features Ø Ø Ø Optimal combination results in lowest risk for given return Efficient frontier describes optimal trade-off Portfolios on efficient frontier are dominant Investments 9 13

Efficient Frontier E[r] Efficient frontier Global minimum variance portfolio Individual assets Minimum variance frontier St. Dev. Investments 9 14

Wrap-up How to estimate portfolio return and risk? q What is the mean-variance frontier? q What is the efficient portfolio frontier? q Why do portfolios on efficient frontier dominate other combinations? q Investments 9 15