Efficient Differential Evolution using Speciation for Multimodal Function

Efficient Differential Evolution using Speciation for Multimodal Function Optimization Cthsieh 2006. 03. 15

Author and Source n Author : Xiaodong Li n Source : GECCO’ 05 , page 873~880

Outline n Introduction n The Basics on Differential Evolution (DE) n The Concept of Crowding and Crowding. DE n Species-Based Differential Evolution (SDE) n Numerical Results n Conclusion

Introduction n DE proposed by Storn and Price in 1995 n A branch of Evolutionary Algorithm n Population-Based n Using vector differences for perturbing the vector population n Few control variables, easy to use and very well to parallel computation

Introduction (cont. ) n For Multimodal Problem, all the multiple optima must be located (including all the global and some second best optima) n But, DE Originally designed for single global optimum n Some extend DE to handle Multimodal problem MMDE (multiresolution multipopulation DE) (2004) n Multi. DE (2004) n Crowding. DE (2004) n Species-Based DE n

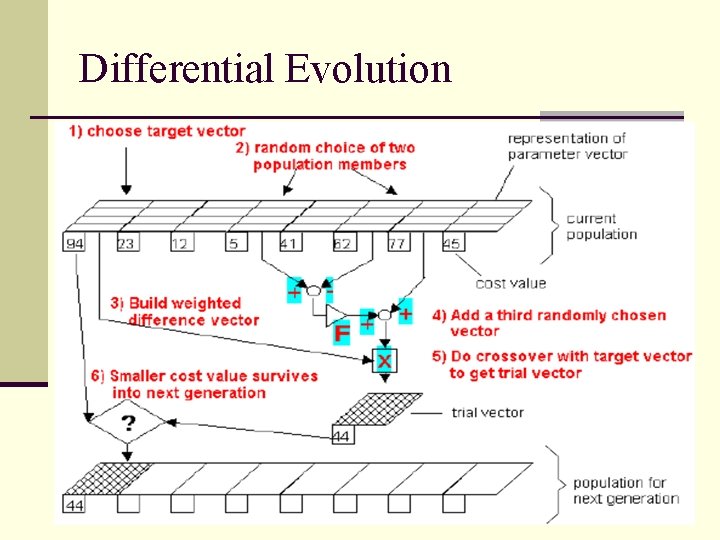
Differential Evolution

Differential Evolution n Utilizing NP parameter vectors as a population n Mutation For each target vector generated according to , a mutant vector is with random indexes n NP must be greater or equal to four and F

Differential Evolution

Differential Evolution n Crossover in order to increase the diversity, the trial vector: Is formed, where n n n : uniform random number generator with outcome : randomly chosen index : crossover rate

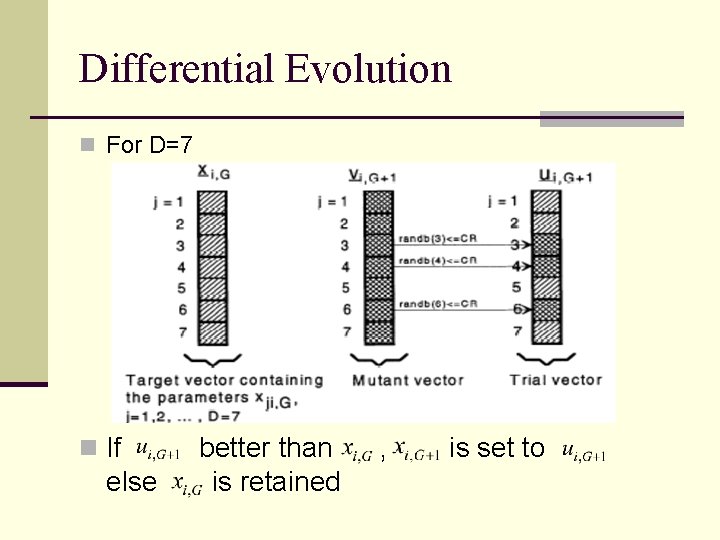
Differential Evolution n For D=7 n If else better than is retained , is set to

The Procedure to generating one offspring n n For all individual of the current population generate new individual for the next iteration to

Crowding DE n n Crowding in GA 1. Randomly pick two parent individual 2. Producing two offspring 3. Randomly select C individual from population 4. Check which individual from C is most similar to this offspring 5. Replace the most similar individual with the offspring C : crowding factor, commonly set to 2 or 3 Similarity : Euclidean distance or Hamming distance Replacement error

Crowding DE 1. Use standard DE to produce an offspring 2. Calculate the Euclidean distance values 3. Sort according to Euclidean distance 4. Compare with the individual has the smallest Euclidean distance, if fitter than replace it 5. Go to step 1 if the number of offspring is smaller than the population size 6. Crowding factor C is set to equal the population size

Crowding DE n Disadvantage suffer from a higher computational cost n Complexity : n Not suitable for large population size n Advantage n Easy to implement n Do not need any user-specified parameters such as species radius in species-based DE n

Species-Based DE n Identifying species user-specified parameters rs

Species-Based DE 1. Initialize population 2. Evaluate all individual 3. Sort all individuals from the best-fit to least-fit 4. Determine the species seeds 5. For each species, run a basic DE 1. If less than m individuals, than generate new individuals within the radius until there are m individuals in the species 2. If a child’s fitness is the same with its species seed, replace the redundant and randomly generated new one 6. Keep only the N fitter individuals 7. Go back to step 2, unless the termination criteria not meet

Complexity of SDE n Euclidean distance calculations required: n But, more tighter upper bound, n is the upper bound of the number of species that will be found at each iteration n estimated according to n Typically, n Linear time complexity of

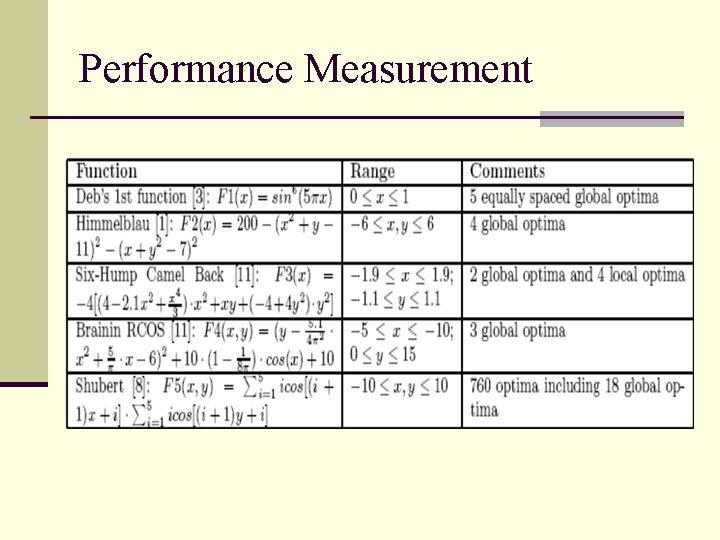
Performance Measurement n Accuracy n Convergence Speed n n : the closest pair of a global optimum and species seed set to 0. 0001

Performance Measurement

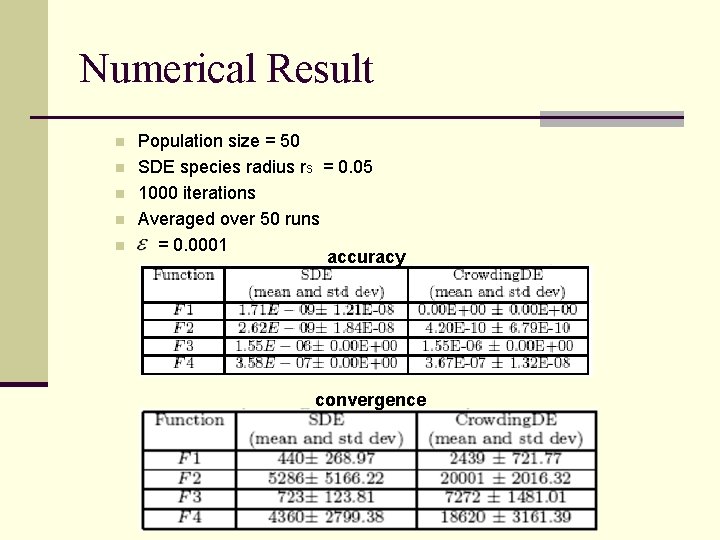
Numerical Result n n n Population size = 50 SDE species radius rs = 0. 05 1000 iterations Averaged over 50 runs = 0. 0001 accuracy convergence

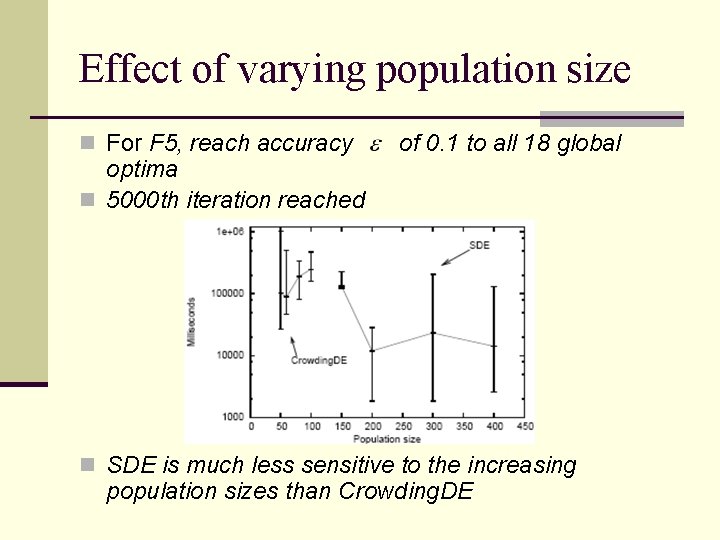
Effect of varying population size n For F 5, reach accuracy optima n 5000 th iteration reached of 0. 1 to all 18 global n SDE is much less sensitive to the increasing population sizes than Crowding. DE

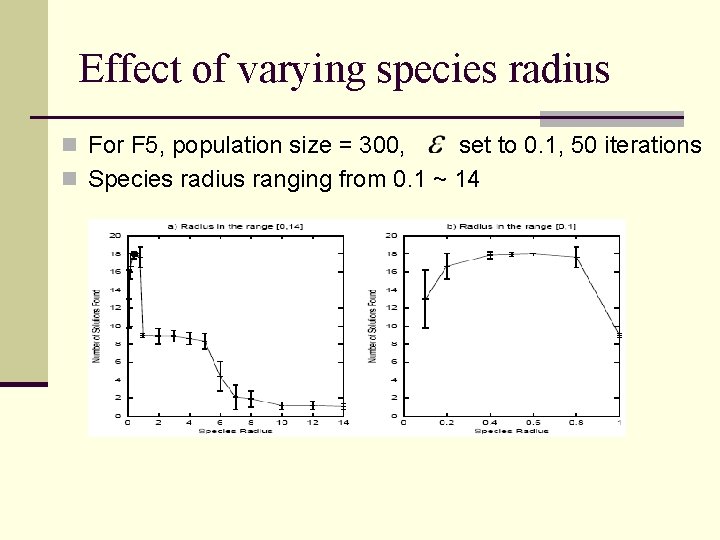
Effect of varying species radius n For F 5, population size = 300, set to 0. 1, 50 iterations n Species radius ranging from 0. 1 ~ 14

Conclusion n Differential Evolution n Crowding Differential Evolution n Species-Based Differential Evolution n Performance comparison