Efficient Craig Interpolation for Linear Diophantine DisEquations and

Efficient Craig Interpolation for Linear Diophantine (Dis)Equations and Linear Modular Equations Presenter : Jen-Chi Lin 9/25/2020 1

Outline ¡ ¡ Introduction LDEs (Linear Diophantine Equations) - Proof of Unsatisfiability 9/25/2020 ¡ - Implication - Partial interpolant - Interpolants for LDEs+LDDs ¡ Algorithms for Obtaining Proofs of Unsatisfiability 2

Introduction ¡ A linear diophantine equation (LDE) rational integral variable ¡ 9/25/2020 A linear diophantine disequation (LDD) 3

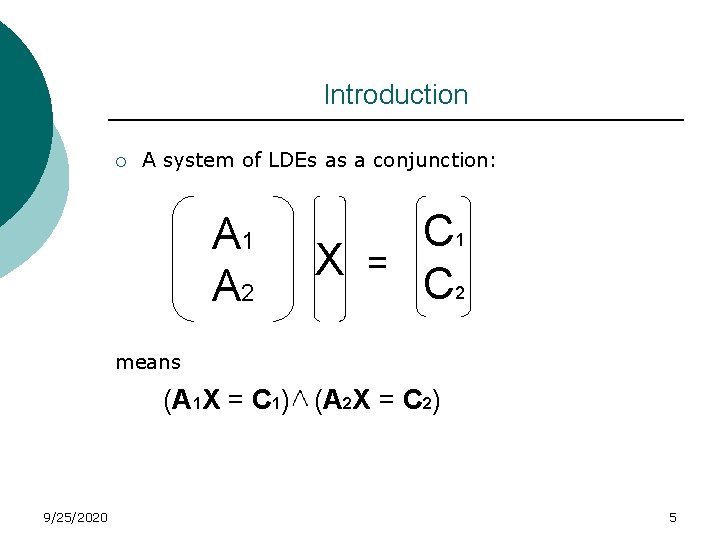
Introduction ¡ A system of LDEs can be written as: A ¡ 9/25/2020 X = C A system of LDDs can be written as: 4

Introduction ¡ A system of LDEs as a conjunction: A 1 A 2 C 1 X = C 2 means (A 1 X = C 1) (A 2 X = C 2) 9/25/2020 5

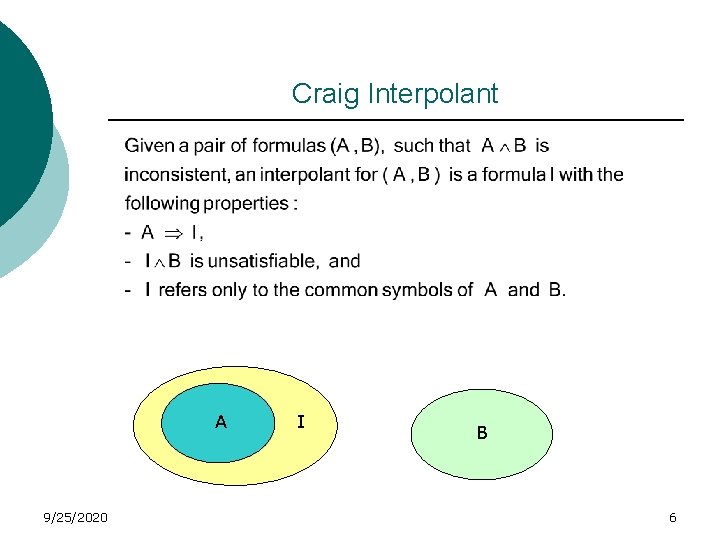
Craig Interpolant A 9/25/2020 I B 6

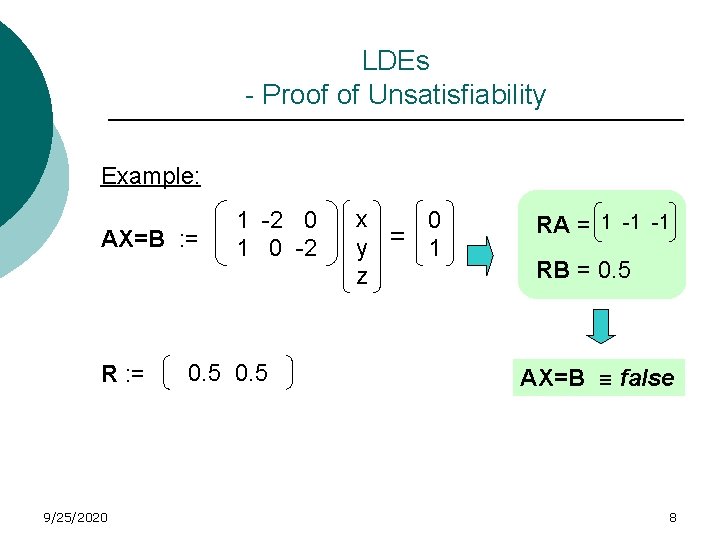
LDEs - Proof of Unsatisfiability ¡ Theorem 1 AX = B ≡ false (i. e no integral solution for X) iff there exists a rational row vector R such that 1) RA is integral 2) RB is not an integer We call R a proof of unsatisfiability for AX=B 9/25/2020 7

LDEs - Proof of Unsatisfiability Example: AX=B : = R : = 9/25/2020 1 -2 0 1 0 -2 0. 5 x 0 y = 1 z RA = 1 -1 -1 RB = 0. 5 AX=B ≡ false 8

LDEs - Implication ¡ Definition 1. (Implication) LDEs CX = D implies a (single) LDE AX =B if every integral vector X satisfying CX = D also satisfies AX = B. 9/25/2020 9

LDEs - Implication ¡ Lemma 1. (Linear combination) For every rational row vector U LDEs CX = D implies the LDE UCX = UD CX = D also implies the LME UCX≡m UD for any rational number m. 9/25/2020 10

How to compute Interpolants for LDEs? ¡ implies (AX = A’) (CX=D) (BX = B’) ≡ false CX = D refers only to common to A, B Only to xi who have coefficients ≠ 0 in A and in B 9/25/2020 11

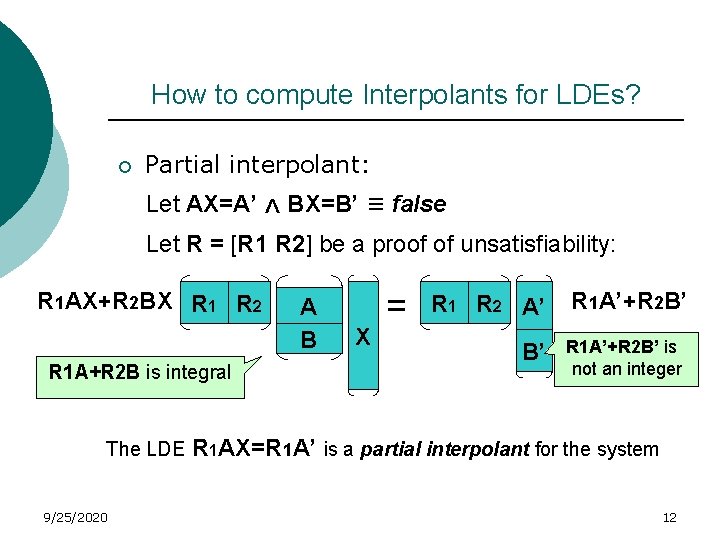
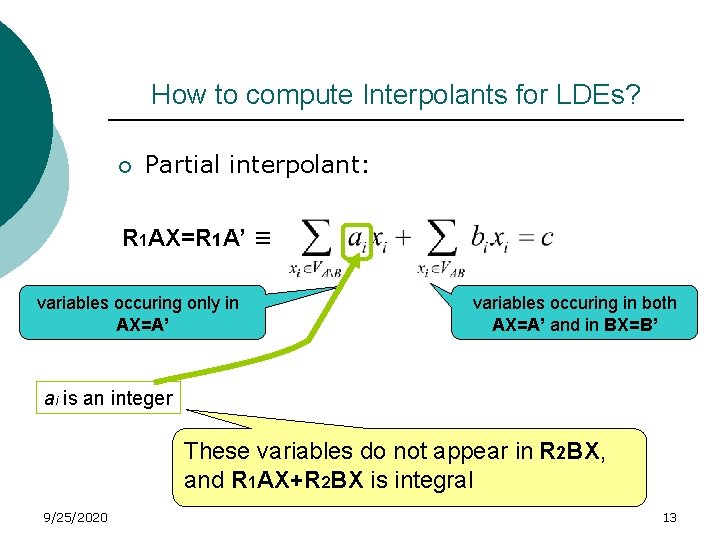
How to compute Interpolants for LDEs? ¡ Partial interpolant: Let AX=A’ ^ BX=B’ ≡ false Let R = [R 1 R 2] be a proof of unsatisfiability: R 1 AX+R 2 BX R 1 R 2 R 1 A+R 2 B is integral The LDE 9/25/2020 A B X = R 1 R 2 A’ B’ R 1 A’+R 2 B’ is not an integer R 1 AX=R 1 A’ is a partial interpolant for the system 12

How to compute Interpolants for LDEs? ¡ Partial interpolant: R 1 AX=R 1 A’ ≡ variables occuring only in AX=A’ variables occuring in both AX=A’ and in BX=B’ ai is an integer These variables do not appear in R 2 BX, and R 1 AX+R 2 BX is integral 9/25/2020 13

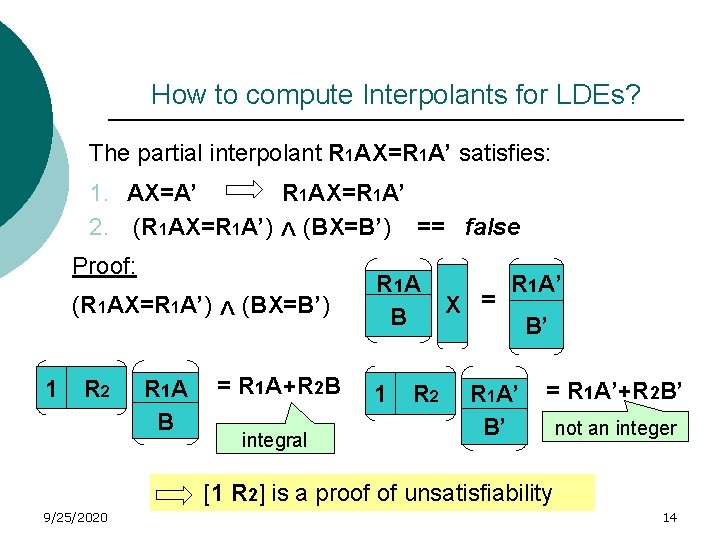
How to compute Interpolants for LDEs? The partial interpolant R 1 AX=R 1 A’ satisfies: 1. AX=A’ R 1 AX=R 1 A’ 2. (R 1 AX=R 1 A’) (BX=B’) == false ^ Proof: (R 1 AX=R 1 A’) 1 R 2 R 1 A B ^ (BX=B’) R 1 A’ = X B B’ = R 1 A+R 2 B 1 integral R 2 R 1 A’ B’ = R 1 A’+R 2 B’ not an integer [1 R 2] is a proof of unsatisfiability 9/25/2020 14

How to compute Interpolants for LDEs? R 1 AX=R 1 A’ ≡ If all ai=0, then the partial interpolant is also an interpolant for AX=A’ BX=B’: We saw the first two conditions hold. In case ai=0 , then R 1 AX=R 1 A’ is over variables common to AX=A’ and to BX=B’. 9/25/2020 15

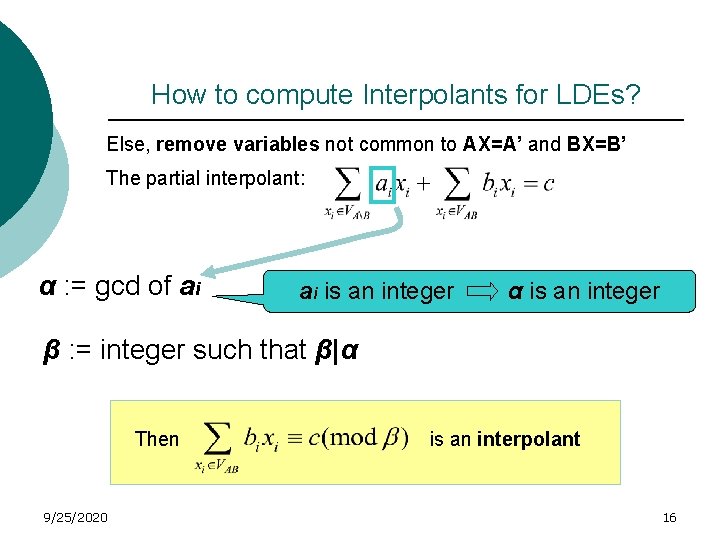
How to compute Interpolants for LDEs? Else, remove variables not common to AX=A’ and BX=B’ The partial interpolant: α : = gcd of ai ai is an integer α is an integer β : = integer such that β|α Then 9/25/2020 is an interpolant 16

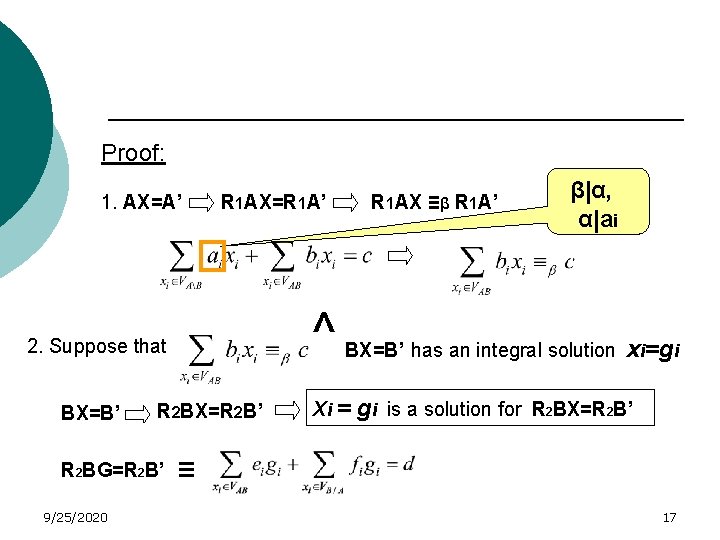
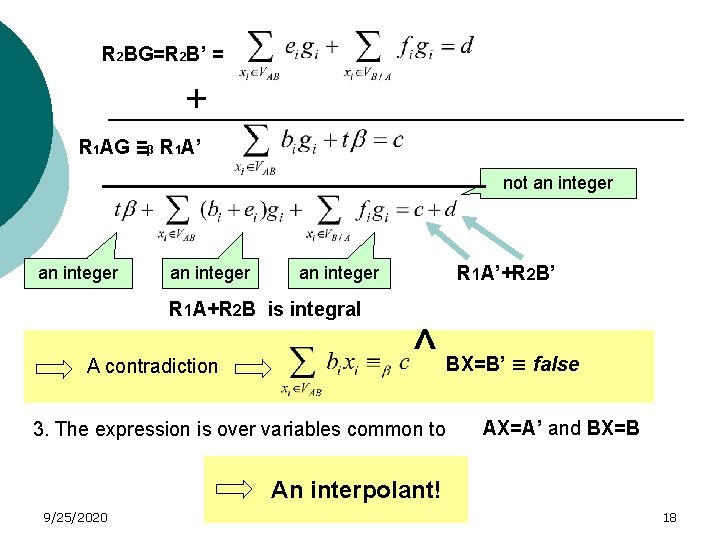
Proof: 1. AX=A’ R 1 AX=R 1 A’ ^ 2. Suppose that BX=B’ R 2 BX=R 2 B’ R 2 BG=R 2 B’ 9/25/2020 R 1 AX ≡β R 1 A’ β| α , α | ai BX=B’ has an integral solution Xi = xi=gi gi is a solution for R 2 BX=R 2 B’ ≡ 17

R 2 BG=R 2 B’ = + R 1 AG ≡β R 1 A’ not an integer R 1 A+R 2 B is integral A contradiction R 1 A’+R 2 B’ an integer ^ 3. The expression is over variables common to BX=B’ ≡ false AX=A’ and BX=B An interpolant! 9/25/2020 18

How to compute Interpolants for LDEs? - Algorithm Given AX=A’ BX=B’ ≡ false : 1. compute a proof of unsatisfiability [R 1 R 2] 2. compute the partial interpolant R 1 AX=R 1 A’ 3. if R 1 AX=R 1 A’ is not only over VAB : 3. 1 compute the gcd α of coefficients of xi’s in VAB 3. 2 compute β that divides α 3. 3 return else return R 1 AX=R 1 A’ 9/25/2020 19

LDEs+LDDs ¡ Theorem 2. The following are equivalent: 1. F has no integral solution 2. F has no rational solution or AX = B has no integral solution. 9/25/2020 20

LDEs+LDDs ¡ Proof - Lemma 2. A system of LDEs AX = B implies a LDE EX = F iff AX = B is unsatisfiable or there exists a rational vector R such that E = RA and F = RB - Lemma 3. A system of LDEs AX = B implies iff there exists 1≦ k ≦m such that AX = B implies Ck. X = Dk. 9/25/2020 21

LDEs+LDDs ¡ Proof → (1) → (2) (1) is easy. (2): Lemma 3 Lemma 2 9/25/2020 22

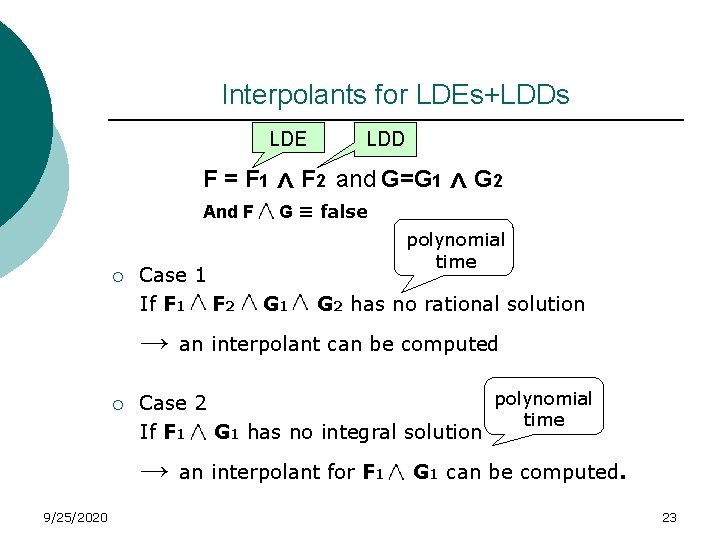
Interpolants for LDEs+LDDs LDE F = F 1 And F ¡ Case 1 If F 1 F 2 → ¡ F 2 and G=G 1 ^G ≡ false ^ G 2 polynomial time G 1 G 2 has no rational solution an interpolant can be computed polynomial Case 2 time If F 1 G 1 has no integral solution → 9/25/2020 LDD an interpolant for F 1 G 1 can be computed. 23

Algorithms for Obtaining Proofs of Unsatisfiability If AX= B has no rational solution → no integral solution. Use Gaussian elimination If AX= B has a rational solution Use Hermite Normal Form (HNF) 9/25/2020 24

polynomial time Hermite Normal Form Every full row rank matrix A[mxn] can be represented as: m xm Lower triangular mx(n-m) E 0 Maximal element lies on the diagonal Invertible All entries non-negative The HNF form can be obtained by using the three basic column operations on A Lemma: AX=B has no integral solution iff E-1 B is not integral 9/25/2020 25

Proof of Unsatisfiability To obtain R, a proof of unsatisfiability: 1. Compute [E 0] 2. If E-1 B is not integral: 2. 1. E-1 B[i] is not an integer. R’ = the i-th row in E-1 R’B is not an integer, R’A is integral Proof: AU = [E 0] E-1 AU = E-1[E 0] = [I 0] 9/25/2020 Integral E-1 AUU-1= E-1 A = [I 0] U-1 26

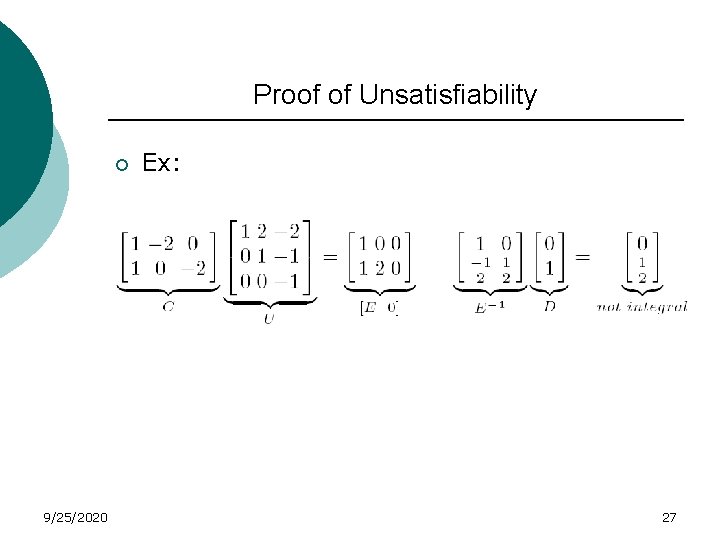
Proof of Unsatisfiability ¡ 9/25/2020 Ex: 27