Efficient Computation of Frequent and Topk Elements in

Efficient Computation of Frequent and Top-k Elements in Data Streams 1

Motivation Motivated by Internet advertising commissioners n Before rendering an advertisement for user, query clicks stream for advertisements to display. n If the user's profile is not a frequent “clicker”, then s/he will probably not click any displayed advertisement. n – Show Pay-Per-Impression advertisements. n If the user's profile is a frequent “clicker”, then s/he may click a displayed advertisement. – Show Pay-Per-Click advertisements. – Retrieve top advertisements to choose what to display. 2

Problem Definition Given alphabet A, stream S of size N, a frequent element, E, is an element whose frequency, F, exceeds a user specified support, φN n Top-k elements are the k elements with highest frequency n Both problems: n – Very related, though, no integrated solution has been proposed – Exact solution is O(min(N, A)) space approximate variations 3

Practical Frequent Elements n -Deficient Frequent Elements [Manku ‘ 02]: – All frequent elements output should have F > (φ - )N, where is the user-defined error. φN (φ - ) N 4

Practical Top-k n Find. Approx. Top(S, k, ) [Charikar ‘ 02]: – Retrieve a list of k elements such that every element, Ei, in the list has Fi > (1 - ) Fk, where Ek is the kth ranked element. F 4 (1 - ) F 4 5

The Space-Saving Algorithm n Space-Saving is counter-based n Monitor only m elements n Only over-estimation errors n Frequency estimation is more accurate for significant elements n Keep track of max. possible errors 6

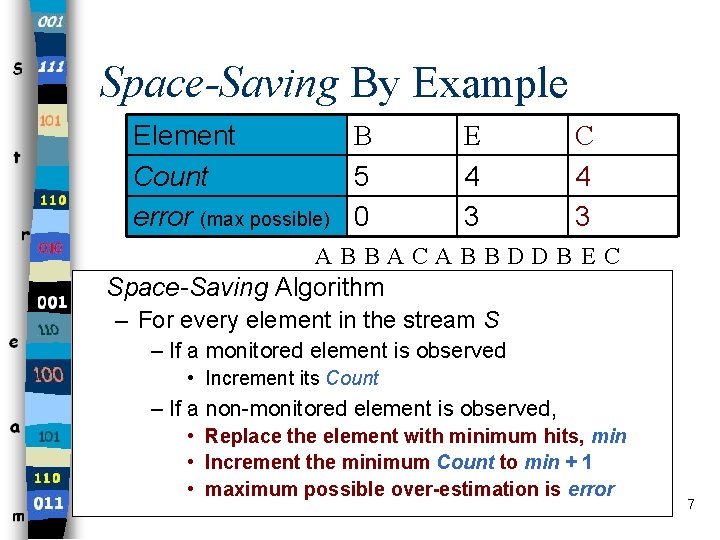
Space-Saving By Example A B Element Count 2 3 4 5 error (max possible) 0 B A E 2 3 4 0 3 C D A 1 2 3 4 1 0 3 ABBACABBDDB E C Space-Saving Algorithm – For every element in the stream S – If a monitored element is observed • Incrementits its. Count – If a non-monitored element is observed, • Replace theelementwithminimum hits, minmin • Increment theminimum Count to to minmin + 1+ 1 • maximum possibleover-estimation is error 7

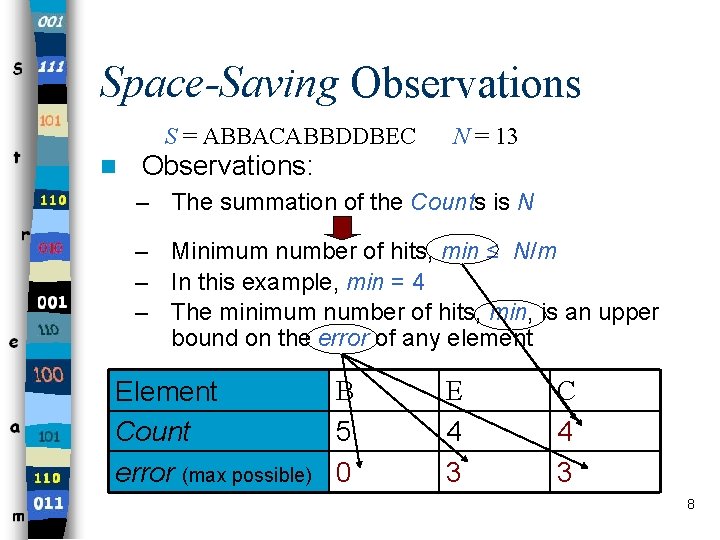
Space-Saving Observations S = ABBACABBDDBEC n N = 13 Observations: – The summation of the Counts is N – Minimum number of hits, min ≤ N/m – In this example, min = 4 – The minimum number of hits, min, is an upper bound on the error of any element B Element Count 5 error (max possible) 0 E 4 3 C 4 3 8

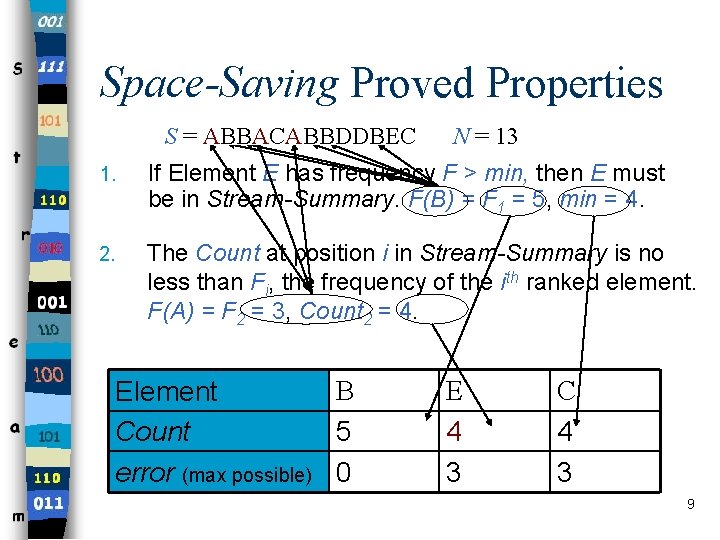
Space-Saving Proved Properties S = ABBACABBDDBEC N = 13 1. If Element E has frequency F > min, then E must be in Stream-Summary. F(B) = F 1 = 5, min = 4. 2. The Count at position i in Stream-Summary is no less than Fi, the frequency of the ith ranked element. F(A) = F 2 = 3, Count 2 = 4. B Element Count 5 error (max possible) 0 E 4 3 C 4 3 9

Space-Saving Data Structure n We need a data structure that – Increments counters in constant time – Keeps elements sorted by their counters n We propose the Stream-Summary structure, similar to the data structure in [Demaine ’ 02] 10

Frequent Elements Queries n Traverse Stream-Summary, and report all elements that satisfy the user support n Any element whose guaranteed hits = (Count – error) > φN is guaranteed to be a frequent element 11

Frequent Elements Example Element B Count error D G A Q F C E 20 14 12 9 7 5 3 3 1 4 1 3 0 1 2 8 8 4 5 2 1 0 Guaranteed Hits = Count - error 19 14 n For N = 73, m = 8, φ = 0. 15: – Frequent Elements should have support of 11 hits. – Candidate Frequent Elements are B, D, and G. – Guaranteed Frequent Elements are B, and D, since their guaranteed hits > 11. 12

Top-k Elements Queries Traverse the Stream-Summary, and report top-k elements. n From Property 2, we assert: n – Guaranteed top-k elements: • Any element whose guaranteed hits = (Count – error) ≥ Countk+1, is guaranteed to be in the top-k. – Guaranteed top-k’ (where k’≈k): • The top-k’ elements reported are guaranteed to be the correct top-k’ iff for every element in the top-k’, guaranteed hits = (Count – error) ≥ Countk’+1. 13

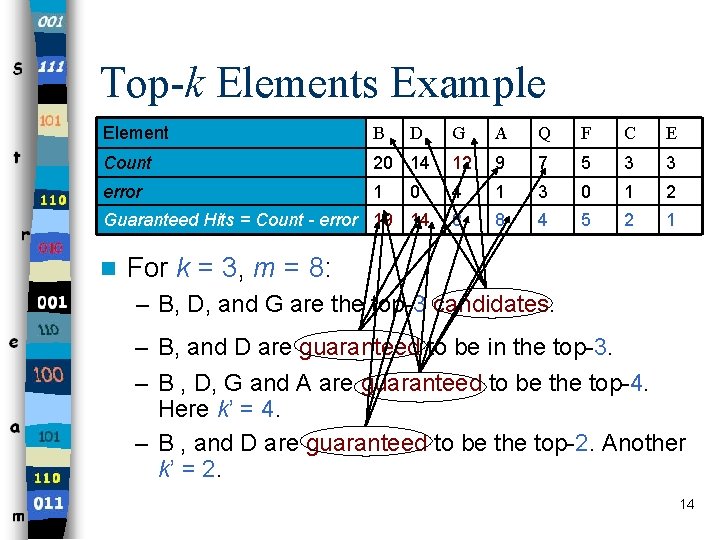
Top-k Elements Example Element B Count error D G A Q F C E 20 14 12 9 7 5 3 3 1 4 1 3 0 1 2 8 8 4 5 2 1 0 Guaranteed Hits = Count - error 19 14 n For k = 3, m = 8: – B, D, and G are the top-3 candidates. – B, and D are guaranteed to be in the top-3. – B , D, G and A are guaranteed to be the top-4. Here k’ = 4. – B , and D are guaranteed to be the top-2. Another k’ = 2. 14

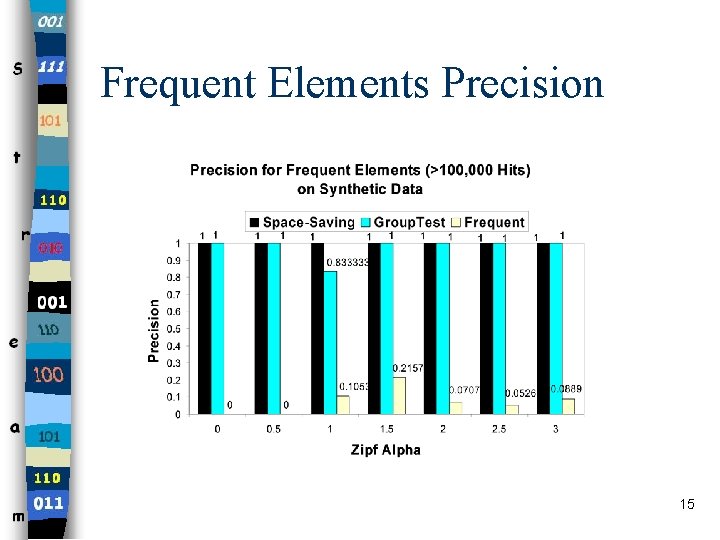
Frequent Elements Precision 15

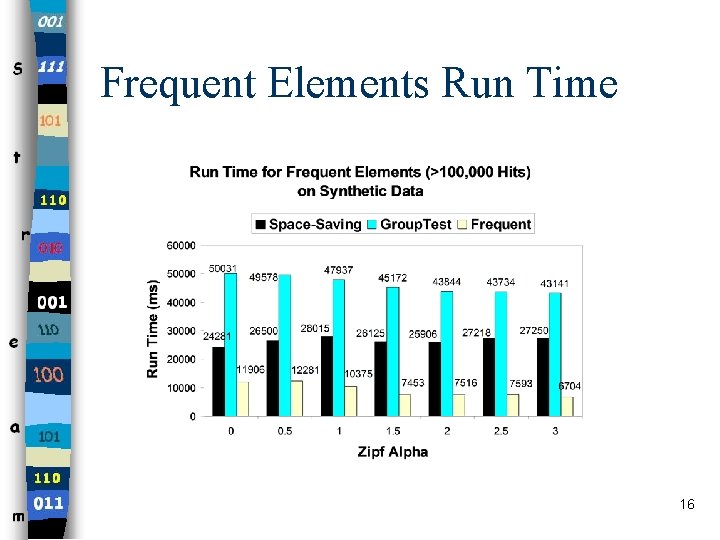
Frequent Elements Run Time 16

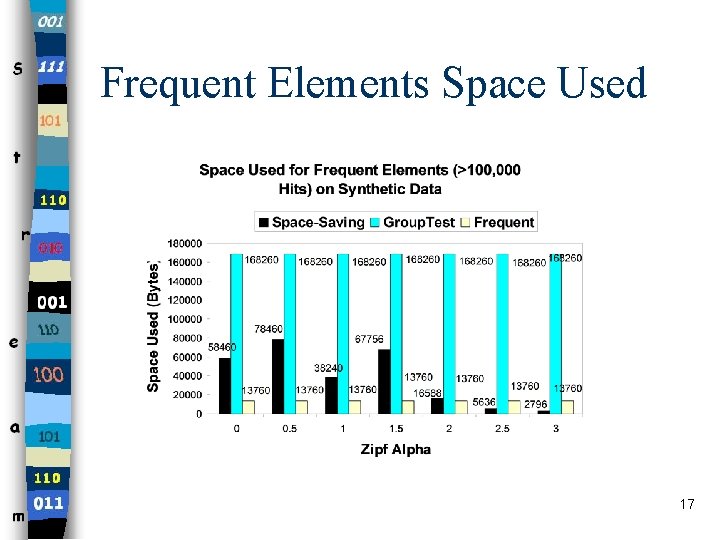
Frequent Elements Space Used 17

Max freq. element in stream n Can we promise to find it with less than m buckets? 18