Efficient collision detection using bounding volume hierarchies of

Efficient collision detection using bounding volume hierarchies of k-DOPs by James T. Klosowski, Martin Held, Joseph S. B. Mitchell, Henry Sowizral, and Karel Zikan Presented by Paul Phipps

Overview • • Background Collision Detection Perspective k-DOP Cost Function Design Choices for BV Tree Tumbling the k-DOPs Experimental Results Future Work

Background • Collision Detection – Pure detection – Detect and report • Do fewer comparisons – Between pairs of objects – Between pairs of primitives • Approaches – Spatial Decomposition • Octrees, k-d trees, BSP-trees, brep-indices, tetrahedral meshes, and (regular) grids – Bounding Volumes Hierarchy • Spheres, axis-aligned bounding boxes (AABBs), oriented bounding box (OBB) (“RAPID” uses OBBTrees) – Miscellaneous

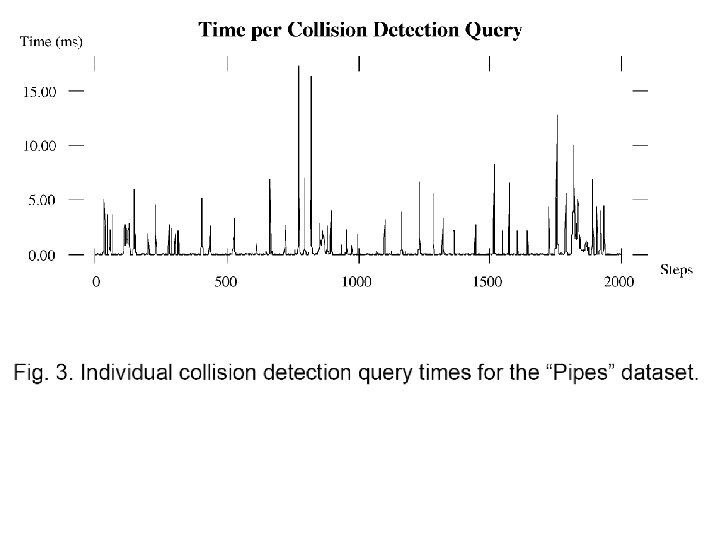
Collision Detection Perspective • Assumptions – Rigid bodies – Discrete points in time • Typical input: – Static object (the environment) – Moving object (the flying hierarchy) • Goals: – Accuracy – Real-time rates • Haptics can require over 1000 collision queries per second
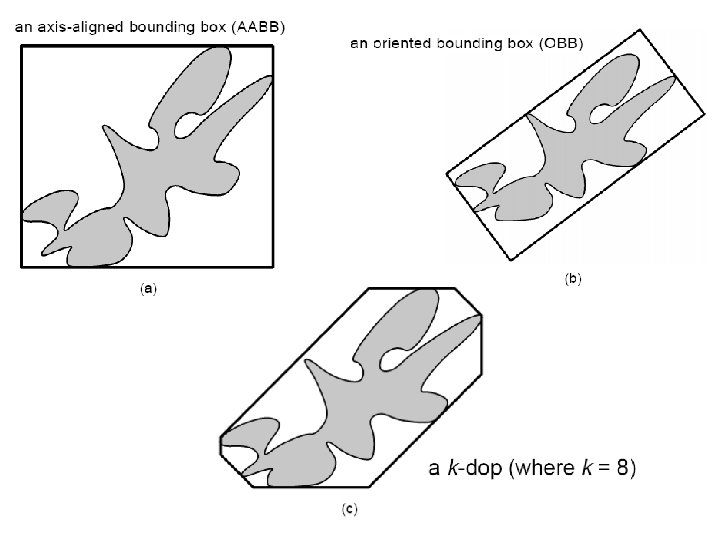

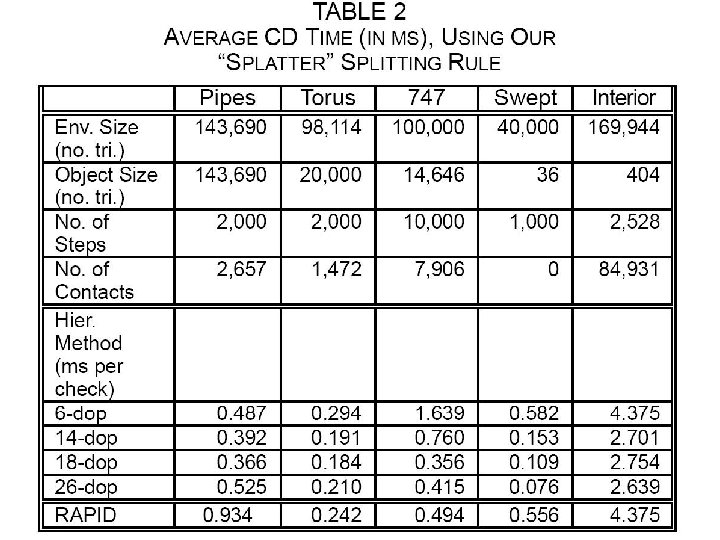
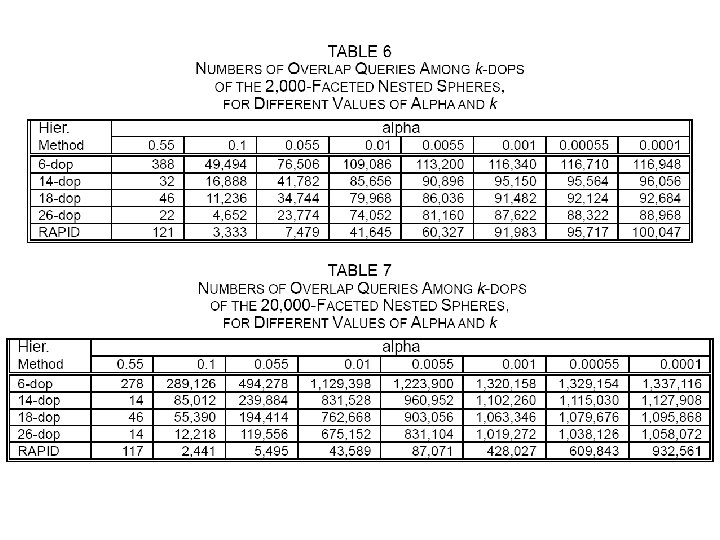
Contributions… • “k-DOP” (Discrete Orientation Polytope) – convex polytope whose facets are determined by halfspaces whose outward normals come from a small fixed set of k orientations – Axis Aligned Bounding Box == 6 -DOP – ((using axes +x, -x, +y, -y, +z, and -z) • k-DOPs used in experiments: – 6 -DOP, 14 -DOP, 18 -DOP, 26 -DOP

…Contributions • Compare ways to construct a Bounding Volume Hierarchy (“BV-tree”) of k-DOPs • Algorithms – Maintain k-DOP BV-tree for moving objects • Translation • Rotation – Fast collision detection • Using BV-trees of moving object and of environment • Results with real and simulated data


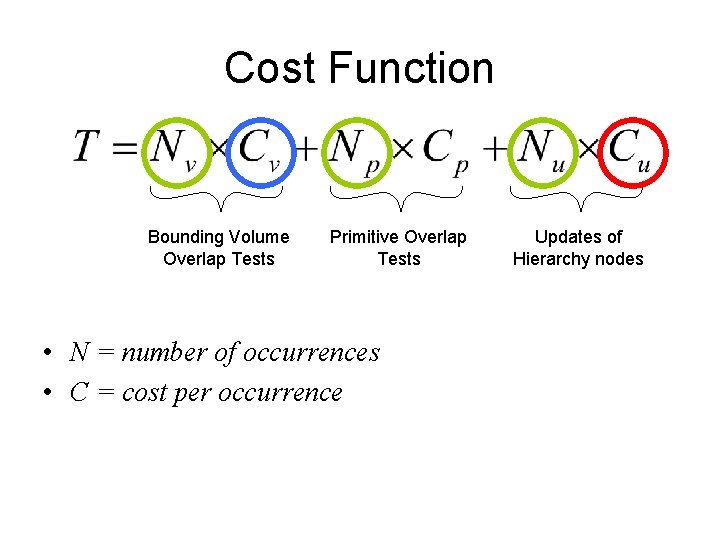
Cost Function Bounding Volume Overlap Tests Primitive Overlap Tests • N = number of occurrences • C = cost per occurrence Updates of Hierarchy nodes

k-DOP Advantages over other BV • Tighter fit than AABB or Sphere – The higher the k the lower Nv, Np, and Nu • Only k values to remember for a BV (using opposite-pointing orientations) • Simpler overlap tests than OBB – Just do (k / 2) interval overlap tests • The parameter k can be chosen to get a good balance between tight fit and quick overlap test

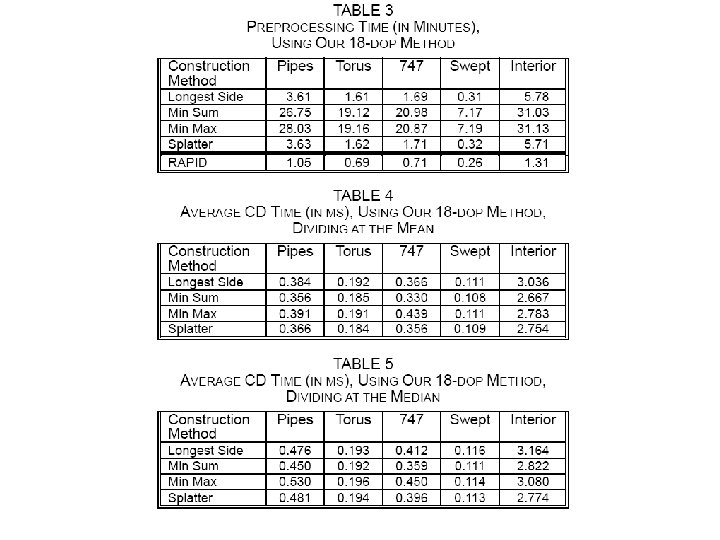
Design Choices for BV Tree • Branching degree 2 (binary tree) is good – Simple to implement – Simple to traverse tree • Splitting rule for pre-computing the tree structure – Pick either x, y, or z axis (using various tests) – Sort along that axis, then use • Median • Mean – Recur
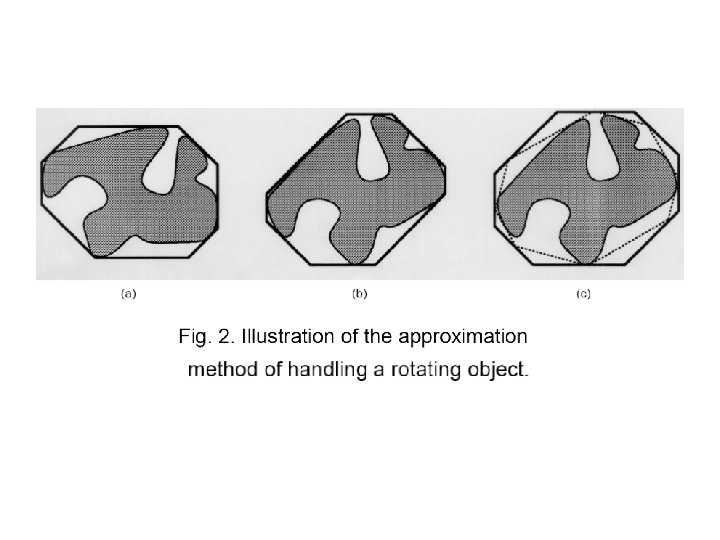

Tumbling the k-DOPs • “hill climbing” method For Root Node – Use pre-computed convex hulls – Are extreme vertices still extreme? • If not, “climb” to more extreme neighbors – Advantage: tight • “approximation method” For non-Root Nodes – Rotate vertices of k-DOP • Get new k-DOP • Don’t accumulate error: Rotate from pre-computed vertices in Model-Space – Advantage: fast

Algorithm 1
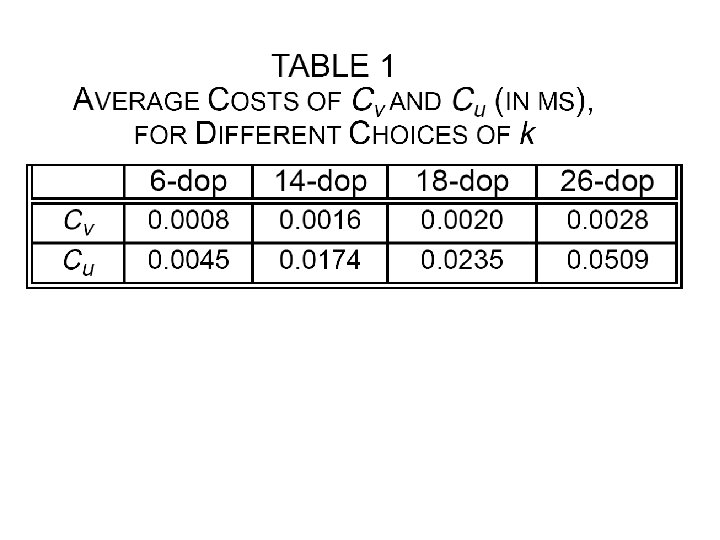
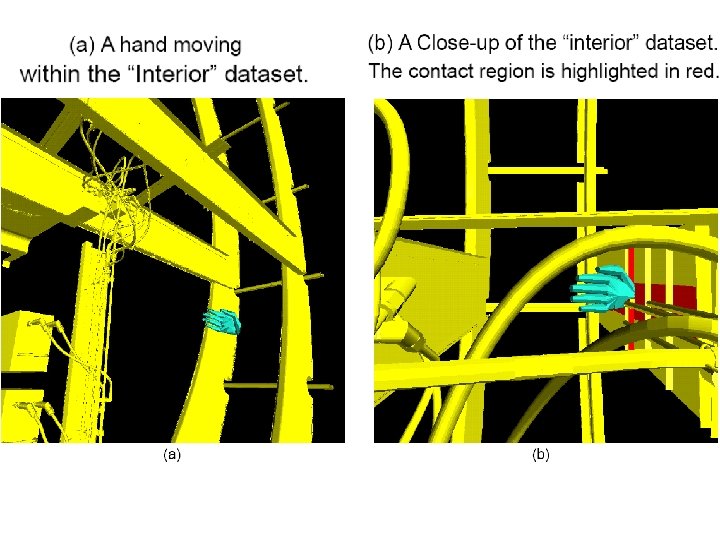

Future Work • • • Use of temporal coherence Multiple flying objects Dynamic environments Deformable objects Numerically Controlled Verification

Overview • • Background Collision Detection Perspective k-DOP Cost Function Design Choices for BV Tree Tumbling the k-DOPs Experimental Results Future Work

Questions?
Continuous Collision Detection of Deformable Objects using k-DOPs
- Slides: 25