EFFICIENT ARCHITECTURES FOR EIGEN VALUE DECOMPOSITION By NIKHIL

EFFICIENT ARCHITECTURES FOR EIGEN VALUE DECOMPOSITION By NIKHIL SURYANARAYANAN

Outline � Motivation � Eigen Value Decomposition & Applications � Exact Jacobi � Parallel Decomposition using Systolic Array � Optimization of Systolic Array � Interconnect optimized Systolic Array � Conclusion

Motivation � Required in various fields � High Performance and Real time applications demands Hardware implementation � SDMA Communication � Realizing optimal architectures with respect to speed and power for respective applications

Eigen Value Decomposition � Angle of Arrival Estimation � Face Detection � Image Compression � Eigen Beam-forming � Signal Subspace Estimation � PCA � MUSIC & ESPRIT

EVD Methods � Exact Jacobi � Systolic Array � Approximate � Algebraic Jacobi Method (only for 3 x 3 matrix)

Eigen Value Decomposition (EVD) Special case of Singular Value Decomposition (SVD) where the Matrix is Square-Symmetric � Consider a Matrix AЄRmxn SVD: A = UDVT EVD: A = UDUT where, DЄRmxn is diagonal matrix, UЄRmxn & VЄRmxn are orthogonal �

CORDIC � COordinate Rotation DIgital Computer � Set of Shift Add Algorithms for computing Sine, Cosine, Arc, Hyperbolic, Coordinate Rotation etc � Eliminates complex computations � Single Shift-Add Multiplier, ROM/RAM for lookup & Basic Logic gates � Hardware friendly � Iterative Algorithm

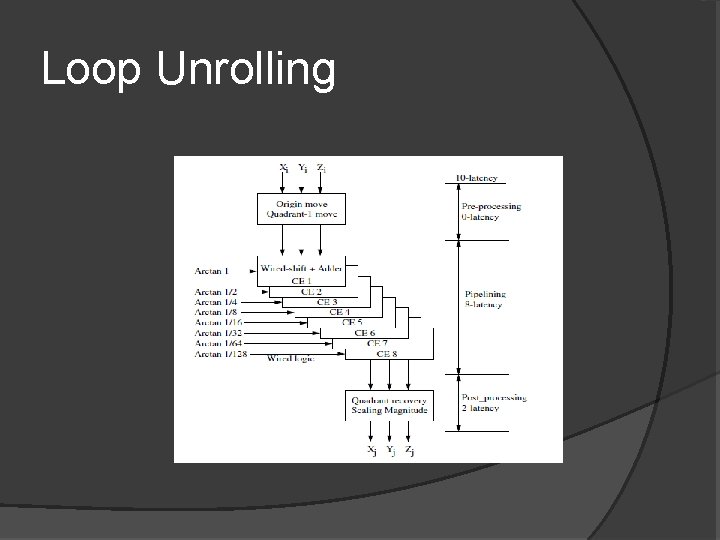
Loop Unrolling

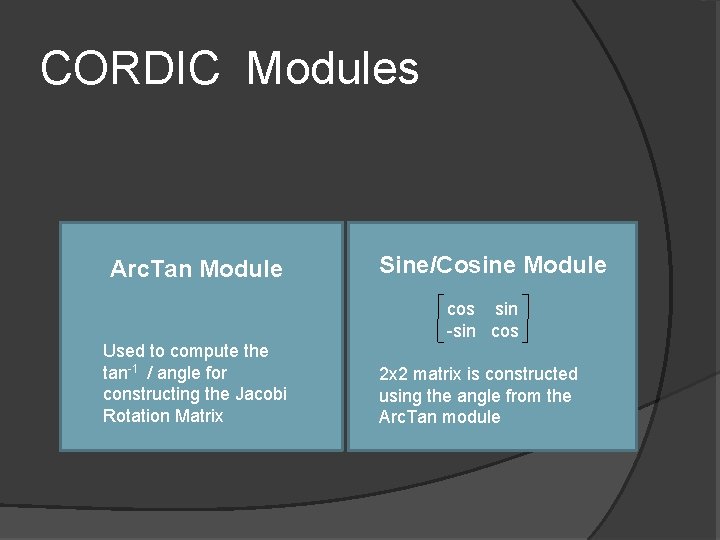
CORDIC Modules Arc. Tan Module Sine/Cosine Module cos sin -sin cos Used to compute the tan-1 / angle for constructing the Jacobi Rotation Matrix 2 x 2 matrix is constructed using the angle from the Arc. Tan module

Exact Jacobi � Aims at annihilating the off diagonal elements using a series of orthogonal transformations � A(k+1) = JTpq A(k) Jpq, where A(0)=A Jpq is called the Jacobi Rotation Defined by the parameter (c s, -s c)

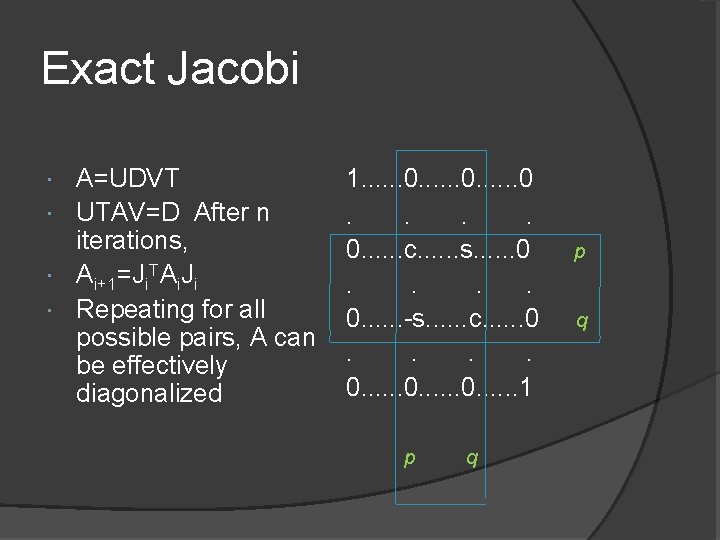
Exact Jacobi A=UDVT UTAV=D After n iterations, Ai+1=Ji. TAi. Ji Repeating for all possible pairs, A can be effectively diagonalized 1. . . 0. . . c. . . s. . . 0. . . -s. . . c. . . 0. . . 1 p q

Limitations of Exact Jacobi Implementation Jacobi iterations are serial � Inability to derive parallelism as iterations have large inter-loop Data Dependency � Inability to pipeline � Every iteration involves transfer of 4 N-4 matrix elements to the processor � Even though it is “MATRIX” operation, parallelism cannot be derived �

How to parallelize? Systolic Array � Solve 2 x 2 EVD sub problems � For a matrix of size N we have N/2 x. N/2 EVD sub problems � If N=6; possible sets are { (1, 2), (3, 4) } { (1, 3), (2, 4) } { (1, 4), (2, 3) } � Parallel Reordering �

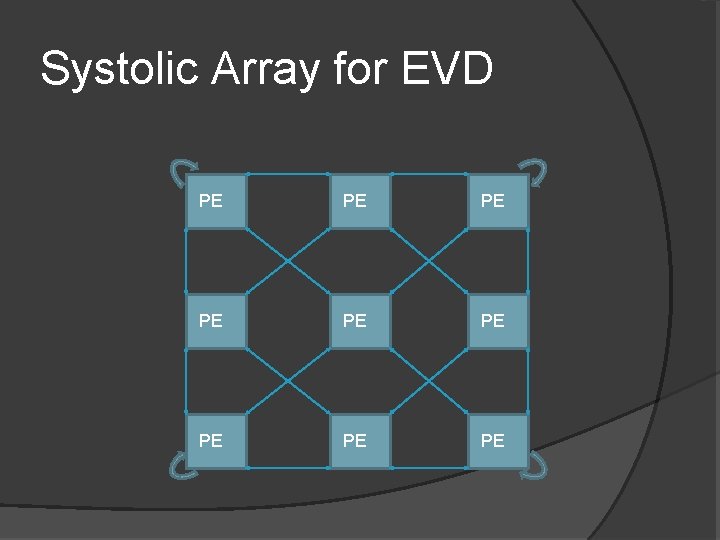
Systolic Array for EVD PE PE PE

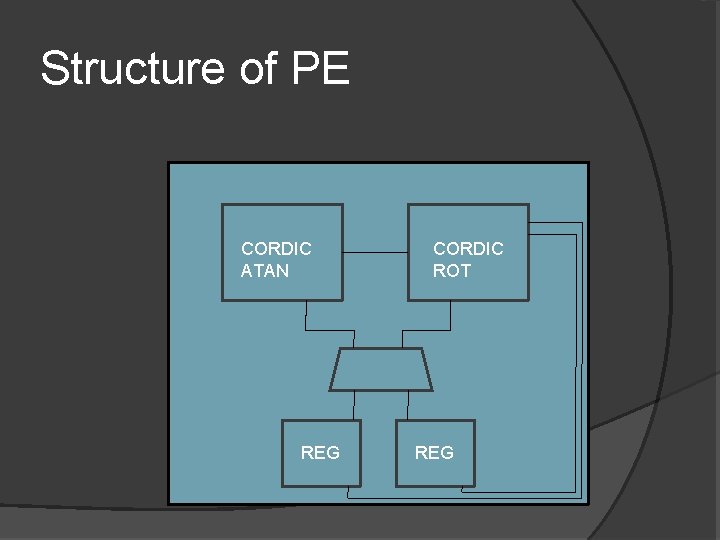
Structure of PE CORDIC ATAN REG CORDIC ROT REG

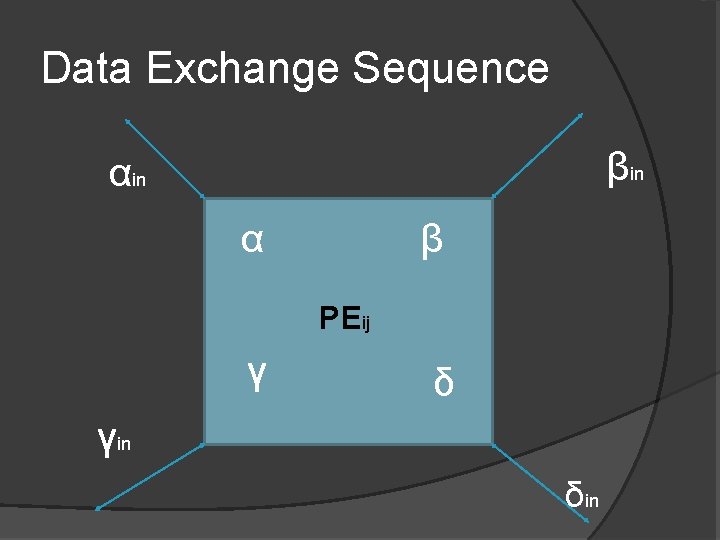
Data Exchange Sequence βin α β PEij γ δ γin δin

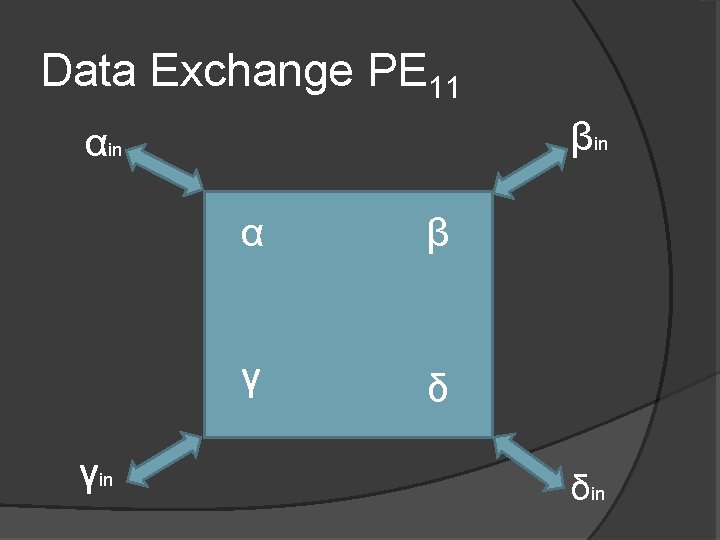
Data Exchange PE 11 βin αin γin α β γ δ δin

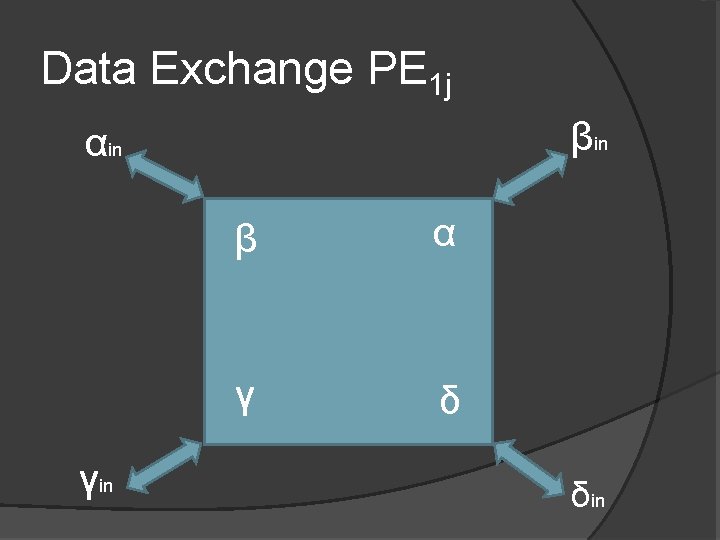
Data Exchange PE 1 j βin αin γin β α γ δ δin

Data Exchange PEi 1 βin αin γ δ α β δin

Data Exchange PEij βin αin γin δ γ β α δin

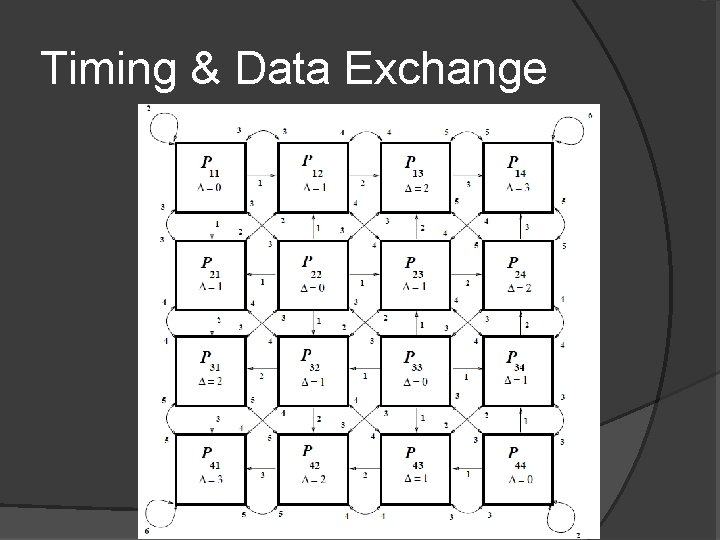
Timing & Data Exchange

Array Cycle ∆ = 1 1 1

Array Cycle ∆ = 1 1 1 1

Array Cycle ∆ = 1 DATA EXCHANGE 1 1 1

Array Cycle ∆ = 1 DATA EXCHANGE 2 1 1 2 1

Array Cycle ∆ = 1 DATA EXCHANGE 1 2 2 1 1 1

Array Cycle ∆ = 1 DATA EXCHANGE 1 2 2 1 2 1

Array Cycle ∆ = 1 DATA EXCHANGE 3 1 2 3 1

Array Cycle ∆ = 1 DATA EXCHANGE 1 3 3 1 2 2

Array Cycle ∆ = 1 DATA EXCHANGE 1 3 3 1 3 1

Staggered Processing? Not realistic to broadcast row and column angles in real time � ∆ij is the distance of the processor Pij from the diagonal � Also Pij needs data from neighbors Pi+-1, j+-1 (1< i, j < n/2) � Can be made faster by allowing off-diagonal PE to allow execution as soon as the diagonal PE produce angles �

Optimizations CYCLE 2 CYCLE 1 1’ 1 1 1’ Improves the utilization time for each PE from 1/3 rd to 2/3 rd

Comparisons…. Matrix 8 x 8 Iterations for Convergence ≈ 3 Additions ≈ 3500 Multiplications ≈ 7000 Additions ≈ 1500 (less than half) Multiplications ≈ 3000 Swaps/Exchange ≈ 0 Swaps/Exchange = 368 Slower Faster EXACT JACOBI Iterations for Convergence ≈ 22 -25 SYSTOLIC ARRAY

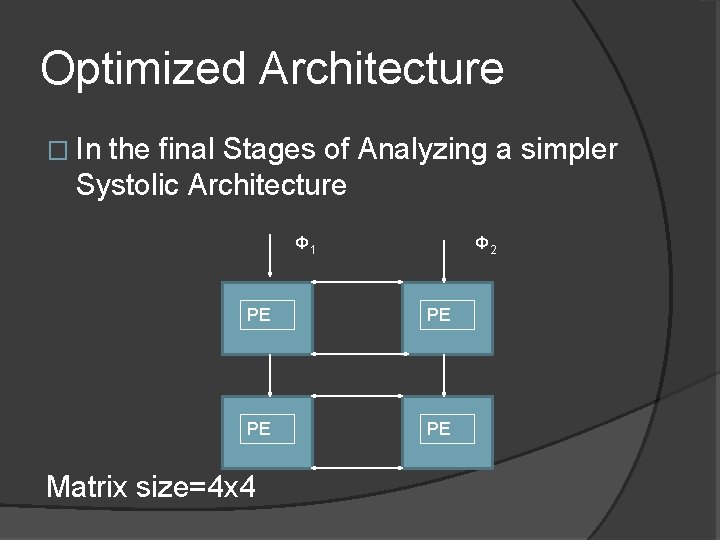
Optimized Architecture � In the final Stages of Analyzing a simpler Systolic Architecture Φ 1 Φ 2 PE PE Matrix size=4 x 4

GOALS � Achieved: Pipelined Jacobi Architecture • S/W Implementation of Systolic Array • Simultaneous execution of off diagonal PE to improve timing and reduce idle time • Optimized Systolic Array architecture for minimum swaps and angle transmission •

References � � � � � Andraka, Ray, “Survey of CORDIC algorithms for FPGA based computers”, ACM 1998 A Novel Implementation of CORDIC Algorithm Using Backward Angle Recoding (BAR), Yu Hen Hu & Homer H. M. Chern, IEEE Transactions on Computers, December 1996 Parallel Eigen Value Decomposition for Toeplitz and Related Matrices, Yu Hen Hu, IEEE Transactions-1989 Kim Y, Doyle James, “A Low Power CMOS CORDIC Processor Design for Wireless Telecommunications”, IEEE 2007 Hemkumar N, Masters Thesis, Rice University Yang Liu et al, “Hardware Efficient Architectures for Eigen Value Computation; , EDA 2006 ASIC Implementation of Autocorrelation and CORDIC algorithm for OFDM based WLAN, Sudhakar Reddy & Ramchandra Reddy, European Journal of Scientific Research, 2009 Advanced Algorithmic Evaluation for Imaging, Communication and Audio Applications – Eigenvalue Decomposition using CATAPULT C Algorithmic Synthesis Methodology Efficient Implementation of SVD on a Reconfigurable System, Christophe Bobda, Klaus Danne and Andre Linarth, Springer -Verlag Berlin Heidelberg 2003 Hardware Implementation of Smart Antenna Systems, H. Wang and M. Glesner, Adv in Radio Sciences 2006 Spectral Estimation using MUSIC Algorithm, Jawed Qumar, Nios II Embedded Processor Design Contest-2005 Hardware Efficient Architectures for Eigen Value Computation, Yang Liu, Christis-Savvas Bouganis, Peter Y. K. Cheung, Philip H. W. Leong, Stephen J. Motley, EDAA 2006 A Novel Fast Eigenvalue Decomposition based on Cyclic Jacobi Rotation and its application in eigen-beamforming, Tech Report of IEICE-Japan Efficient Hardware Architectures for Eigenvector and Signal Subspace Estimation, Fan Xu & Alan Wilson, IEEE Transactions on Circuits & Systems-204 16 BIT CORDIC Rotator for High Sped Wireless LAN, Koushik Maharatna, Alfonso Troya, Swapna Banerjee, Eckhard Grass, Milos Krstic, IEEE Transactions-2004 Survey of CORDIC Algorithms for FPGA Based computers, Ray Andraka, ACM-1998 Smart Antennas for Wireless Communications, Frank B Gross, Mc-Graw Hill, 2005 ( Used for Facts & References for Comparison purposes and Specifications of Different wireless standards)

THANK YOU

QUESTIONS ?

BACK UP SLIDES

Eigen Value and Eigen Vector The non zero vector of any linear transformation when applied to the vector changes the magnitude but not the direction is an Eigen Vector � The scalar value associated with this vector is called the Eigen Value � Ax=λx � A is the transformation, x is the Eigen vector & λ is the corresponding Eigen Value �

CORDIC… contd Convergence depends on number of iterations � Unrolled for Systolic and Pipeline implementations � Iterative architecture unsuitable for FPGA � Pipelined preferred as less complex H/W & operates at data rate � Registers present on Logic cells in FPGAs support pipelining better � Runs at 52 MHz on XC 4013 E-2 [1] �

CORDIC Iteration Equations � Given’s rotation transformation x = x cosΦ – y sinΦ y = y cosΦ + x sinΦ The iteration equations are given as xi+1 = xi – yi. di. 2 -i yi+1 = yi + xi. di. 2 -i zi+1 = zi – di. tan-1(2 -i)

CORDIC Algorithms for i=1: n x 1= x – y * d * (2^-(i-1)) ; y 1= y + x * d * (2^-(i-1)) ; angle = angle – d * (W(i)); if (angle==0) d=0; elseif (angle>0) d=1; else d=-1; end x=x 1; y=y 1; end // W(i) is the i th ROM reference

Exact Jacobi Algorithm for j=1: n-1 for i=n: -1: j+1 J = jacobi_rot( A( i, i), A( j, j), A( i, j) ); A( [ i, j], : )=J'*A( [ i, j], : ); A( : , [ i, j])=A( : , [ i, j] )*J; end REPEAT for n iterations for accuracy

EVD …contd � Also UTU=I and VTV=I � The Diagonal matrix contains Eigen Values along its diagonals � U are the left Singular Vectors & V are right singular vectors � U = {u 1, u 2, ………, un} � V = {v 1, v 2, ………, vn}

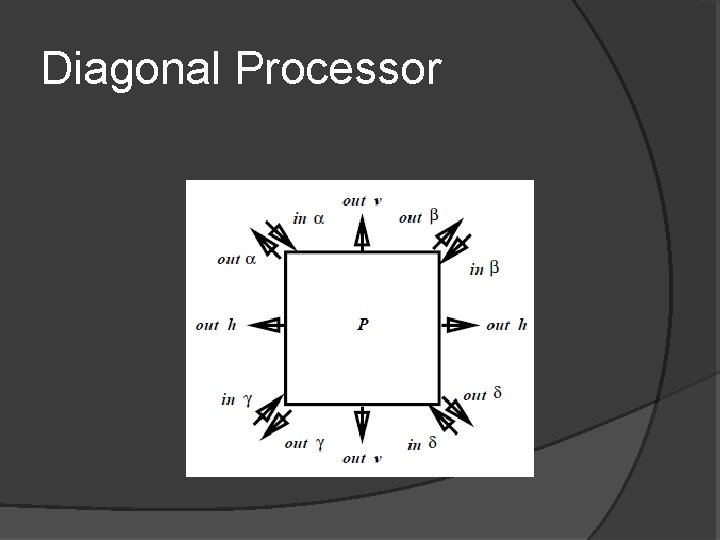
Diagonal Processor

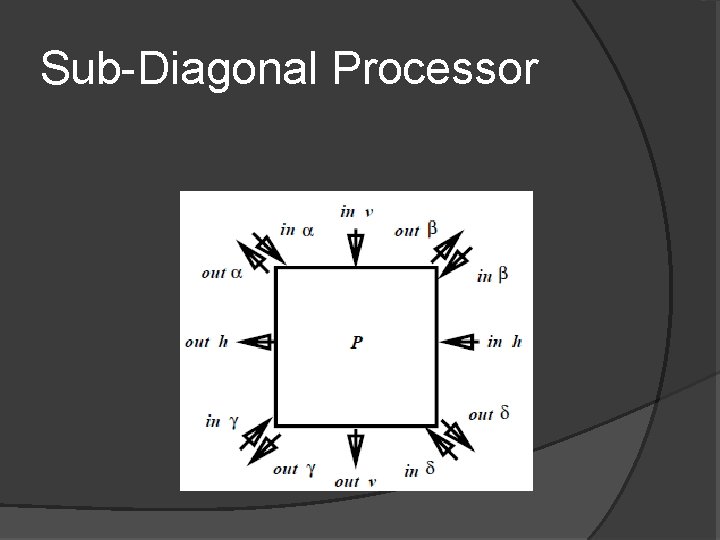
Sub-Diagonal Processor

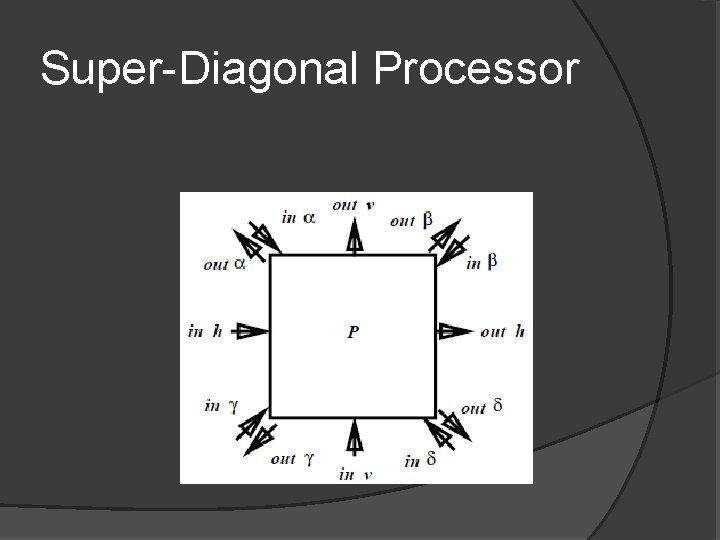
Super-Diagonal Processor