Efficient Approximate Search on String Collections Part II

Efficient Approximate Search on String Collections Part II Marios Hadjieleftheriou Chen Li

Outline l l l Motivation and preliminaries Inverted list based algorithms Gram Signature algorithms Length normalized algorithms Selectivity estimation Conclusion and future directions 2/68

N-Gram Signatures l l l Use string signatures that upper bound similarity Use signatures as filtering step Properties: l l Signature has to have small size Signature verification must be fast False positives/False negatives Signatures have to be “indexable” 3/68

Known signatures l Minhash l l Prefix filter (CGK 06) l l Hamming, Jaccard, Edit distance LSH (GIM 99) l l Jaccard, Edit distance Part. Enum (AGK 06) l l Jaccard, Edit distance Mismatch filter (XWL 08) l Edit distance 4/68

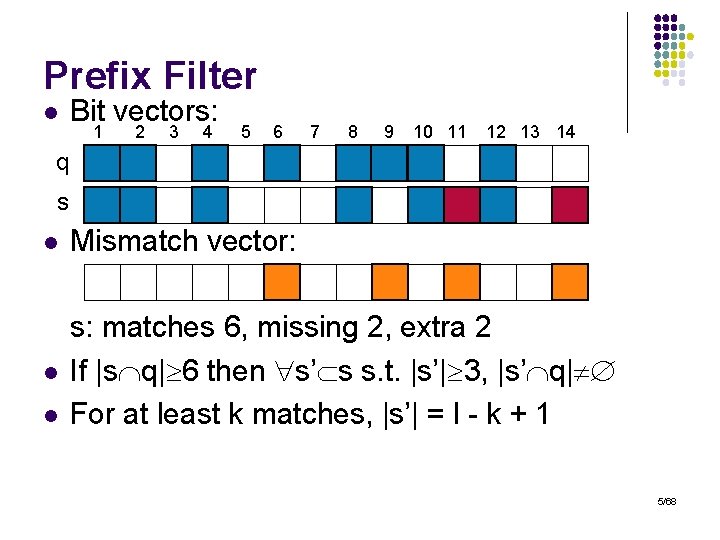
Prefix Filter l Bit vectors: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 q s l Mismatch vector: l s: matches 6, missing 2, extra 2 If |s q| 6 then s’ s s. t. |s’| 3, |s’ q| For at least k matches, |s’| = l - k + 1 l 5/68

Using Prefixes l Take a random permutation of n-gram universe: 6 9 11 14 8 1 2 3 4 5 7 10 12 13 q s l Take prefixes from both sets: l |s’|=|q’|=3, if |s q| 6 then s’ q’ 6/68

Prefix Filter for Weighted Sets l For example: l Order n-grams by weight (new coordinate space) t 1 q t 2 t 4 w 1 w 2 … w 14 t 6 t 8 t 11 t 14 w 1 w 2 0 w 4 0 s w 1 w 2 0 w 4 0 l l Query: w(q s)=Σi q s wi τ Keep prefix s’ s. t. w(s’) w(s) - α w(s)-α s’ l l α s/s’ Best case: w(q/q’ s/s’) = α Hence, we need w(q’ s’) τ - α 7/68

Prefix Filter Properties l l The larger we make α, the smaller the prefix The larger we make α, the smaller the range of thresholds we can support: l l l Because τ α, otherwise τ-α is negative. We need to pre-specify minimum τ Can apply to Jaccard, Edit Distance, IDF 8/68

Other Signatures l l Minhash (still to come) Part. Enum: l l LSH: l l l Upper bounds Hamming Select multiple subsets instead of one prefix Larger signature, but stronger guarantee Probabilistic with guarantees Based on hashing Mismatch filter: l Use positional mismatching n-grams within the prefix to attain lower bound of Edit Distance 9/68

Signature Indexing l Straightforward solution: l l l Create an inverted index on signature n-grams Merge inverted lists to compute signature intersections For a given string q: - Access only lists in q’ Find strings s with w(q’ ∩ s’) ≥ τ - α 10/68

The Inverted Signature Hashtable (CCVX 08) l l Maintain a signature vector for every n-gram Consider prefix signatures for simplicity: l l s’ 1={ ‘tt ’, ‘t L’}, s’ 2={‘t&t’, ‘t L’}, s’ 3=… co-occurence lists: ‘t L’: ‘tt ’ ‘t&t’ … ‘&tt’: ‘t L’ … Hash all n-grams (h: n-gram [0, m]) Convert co-occurrence lists to bit-vectors of size m 11/68

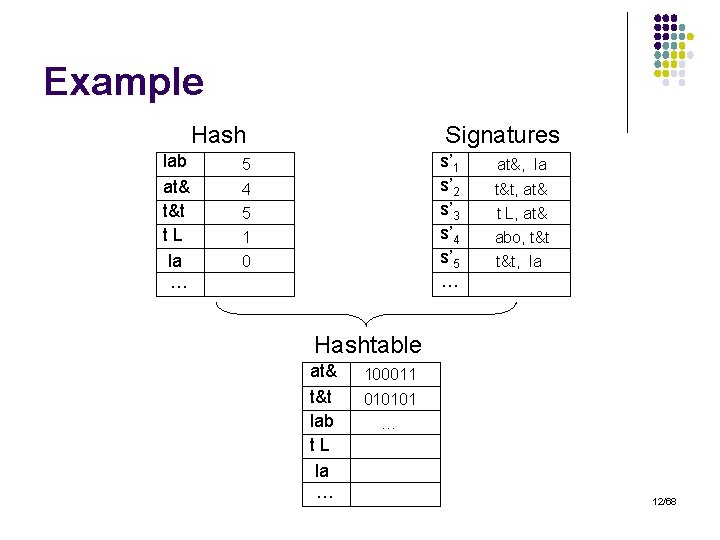
Example Hash lab at& t&t t. L la … Signatures s’ 1 s’ 2 s’ 3 s’ 4 s’ 5 … 5 4 5 1 0 at&, la t&t, at& t L, at& abo, t&t, la Hashtable at& t&t lab t. L la … 100011 010101 … 12/68

Using the Hashtable? l Let list ‘at&’ correspond to bit-vector 100011 l l There exists string s s. t. ‘at&’ s’ and s’ also contains some ngrams that hash to 0, 1, or 5 Given query q: l Construct query signature matrix: q’ q at& lab t&t at& 1 1 lab 1 1 r res … 1 0 … 0 1 … p l l Consider only solid sub-matrices P: r q’, p q We need to look only at r q’ such that w(r) τ-α and w(p) τ 13/68

Verification l How do we find which strings correspond to a given sub-matrix? l l Create an inverted index on string n-grams Examine only lists in r and strings with w(s) τ - l Remember that r q’ Can be used with other signatures as well 14/68

Outline l l l Motivation and preliminaries Inverted list based algorithms Gram Signature algorithms Length normalized algorithms Selectivity estimation Conclusion and future directions 15/68

Length Normalized Measures l What is normalization? l Normalize similarity scores by the length of the strings. - l l Can result in more meaningful matches. Can use L 0 (i. e. , the length of the string), L 1, L 2, etc. For example L 2: - Let w 2(s) Σt sw(t)2 Weight can be IDF, unary, language model, etc. ||s||2 = w 2(s)-1/2 16/68

The L 2 -Length Filter (HCKS 08) l Why L 2? l l For almost exact matches. Two strings match only if: - - They have very similar n-gram sets, and hence L 2 lengths The “extra” n-grams have truly insignificant weights in aggregate (hence, resulting in similar L 2 lengths). 17/68

Example l l l “AT&T Labs – Research” L 2=100 “ATT Labs – Research” L 2=95 “AT&T Labs” L 2=70 l l l If “Research” happened to be very popular and had small weight? “The Dark Knight” “Dark Night” L 2=75 L 2=72 18/68

Why L 2 (continued) l l Tight L 2 -based length filtering will result in very efficient pruning. L 2 yields scores bounded within [0, 1]: l l l 1 means a truly perfect match. Easier to interpret scores. L 0 and L 1 do not have the same properties - - Scores are bounded only by the largest string length in the database. For L 0 an exact match can have score smaller than a non-exact match! 19/68

Example l l l q={‘ATT’, ‘TT ’, ‘T L’, ‘LAB’, ‘ABS’} L 0=5 s 1={‘ATT’} L 0=1 s 2=q L 0=5 S(q, s 1)=Σw(q s 1)/(||q|| ||s 1|| )=10/5 = 2 S(q, s 2)=Σw(q s 2)/(||q|| ||s 2|| )=40/25<2 0 0 20/68

Problems l L 2 normalization poses challenges. l For example: - S(q, s) = w 2(q s)/(||q||2 ||s||2) Prefix filter cannot be applied. Minimum prefix weight α? § § Value depends both on ||s||2 and ||q||2. But ||q||2 is unknown at index construction time 21/68

Important L 2 Properties l Length filtering: l l l For S(q, s) ≥ τ τ ||q||2 ||s||2 ||q||2 / τ We are only looking for strings within these lengths. Proof in paper Monotonicity … 22/68

Monotonicity l l Let s={t 1, t 2, …, tm}. Let pw(s, t)=w(t) / ||s||2 (partial weight of s) Then: S(q, s) = Σ t q s w(t)2 / (||q||2 ||s||2)= Σt q s pw(s, t) pw(q, t) If pw(s, t) > pw(r, t): l l w(t)/||s||2 > w(t)/||r||2 ||s||2 < ||r||2 Hence, for any t’ t: l w(t’)/||s||2 > w(t’)/||r||2 pw(s, t’) > pw(r, t’) 23/68

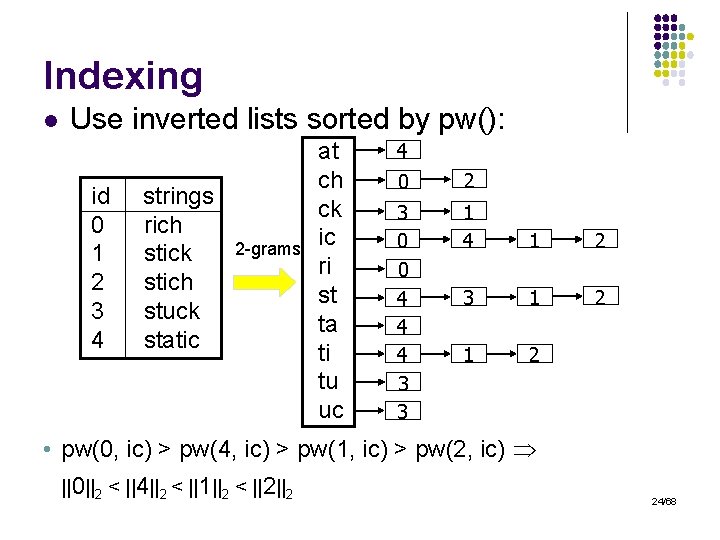
Indexing l Use inverted lists sorted by pw(): id 0 1 2 3 4 strings rich stick stich stuck static 2 -grams at ch ck ic ri st ta ti tu uc 4 0 2 3 0 0 4 4 4 3 3 1 4 1 2 3 1 2 • pw(0, ic) > pw(4, ic) > pw(1, ic) > pw(2, ic) ||0||2 < ||4||2 < ||1||2 < ||2||2 24/68

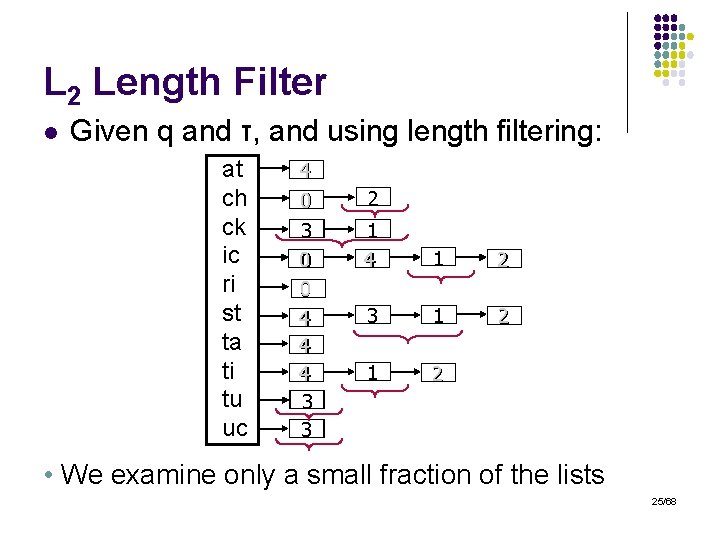
L 2 Length Filter l Given q and τ, and using length filtering: at ch ck ic ri st ta ti tu uc 4 0 3 0 0 4 4 4 3 3 2 1 4 1 2 3 1 2 • We examine only a small fraction of the lists 25/68

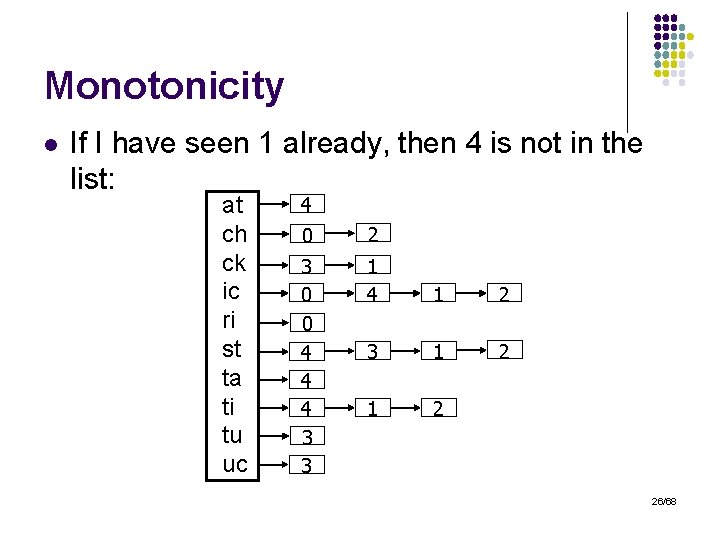
Monotonicity l If I have seen 1 already, then 4 is not in the list: at ch ck ic ri st ta ti tu uc 4 0 2 3 0 0 4 4 4 3 3 1 4 1 2 3 1 2 26/68

Other Improvements l Use properties of weighting scheme l l l Scan high weight lists first Prune according to string length and maximum potential score Ignore low weight lists altogether 27/68

Conclusion l Concepts can be extended easily for: l l l BM 25 Weighted Jaccard DICE IDF Take away message: l l Properties of similarity/distance function can play big role in designing very fast indexes. L 2 super fast for almost exact matches 28/68

Outline l l l Motivation and preliminaries Inverted list based algorithms Gram signature algorithms Length-normalized measures Selectivity estimation Conclusion and future directions 29/68

The Problem l Estimate the number of strings with: l l Edit distance smaller than k from query q Cosine similarity higher than τ to query q Jaccard, Hamming, etc… Issues: l l l Estimation accuracy Size of estimator Cost of estimation 30/68

Motivation l Query optimization: l l l Selectivity of query predicates Need to support selectivity of approximate string predicates Visualization/Querying: l l Expected result set size helps with visualization Result set size important for remote query processing 31/68

Flavors l Edit distance: l l Based on clustering (JL 05) Based on min-hash (MBKS 07) Based on wild-card n-grams (LNS 07) Cosine similarity: l Based on sampling (HYKS 08) 32/68

Selectivity Estimation for Edit Distance l Problem: l l l Given query string q Estimate number of strings s D Such that ed(q, s) δ 33/68

Sepia - Clustering (JL 05, JLV 08) l Partition strings using clustering: l l Store per cluster histograms: l l Enables pruning of whole clusters Number of strings within edit distance 0, 1, …, δ from the cluster center Compute global dataset statistics: l Use a training query set to compute frequency of strings within edit distance 0, 1, …, δ from each query 34/68

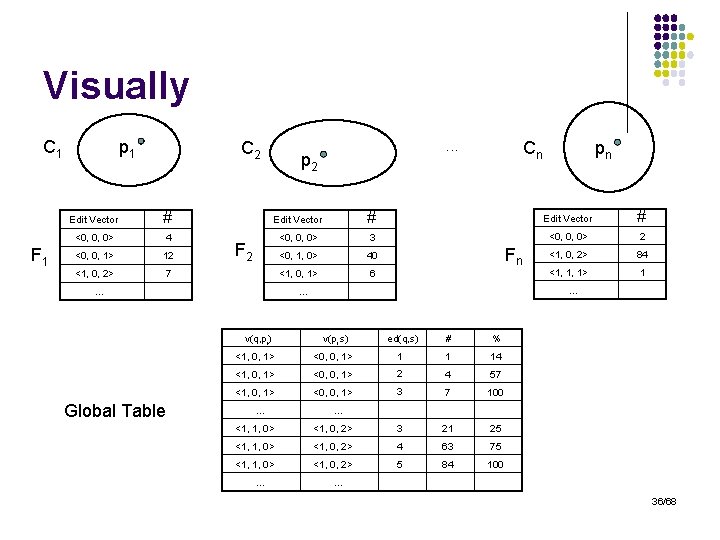
Edit Vectors l Edit distance is not discriminative: l Use Edit Vectors Lukas l <1, 1, 1> 3 q <2, 0, 0> 2 Lucia pi <1, 1, 0> 2 Luciano Ci Lucas 3 D space vs 1 D space 35/68

Visually C 1 F 1 p 1 C 2 . . . p 2 Cn pn Edit Vector # <0, 0, 0> 4 <0, 0, 0> 3 <0, 0, 0> 2 <0, 0, 1> 12 <0, 1, 0> 40 <1, 0, 2> 84 <1, 0, 2> 7 <1, 0, 1> 6 <1, 1, 1> 1 F 2 … … … v(q, pi) Global Table Fn v(pi, s) ed(q, s) # % <1, 0, 1> <0, 0, 1> 1 1 14 <1, 0, 1> <0, 0, 1> 2 4 57 <1, 0, 1> <0, 0, 1> 3 7 100 … … <1, 1, 0> <1, 0, 2> 3 21 25 <1, 1, 0> <1, 0, 2> 4 63 75 <1, 1, 0> <1, 0, 2> 5 84 100 … … 36/68

Selectivity Estimation l Use triangle inequality: l l Compute edit vector v(q, pi) for all clusters i If |v(q, pi)| ri+δ disregard cluster Ci δ ri q pi 37/68

Selectivity Estimation l Use triangle inequality: l l l Compute edit vector v(q, pi) for all clusters i If |v(q, pi)| ri+δ disregard cluster Ci For all entries in frequency table: - If |v(q, pi)| + |v(pi, s)| δ then ed(q, s) δ for all s If ||v(q, pi)| - |v(pi, s)|| δ ignore these strings Else use global table: § § Lookup entry <v(q, pi), v(pi, s), δ> in global table Use the estimated fraction of strings 38/68

Example F 1 Edit Vector # <0, 0, 0> 4 <0, 0, 1> 12 <1, 0, 2> 7 l l δ =3 v(q, p 1) = <1, 1, 0> v(p 1, s) = <1, 0, 2> … Global Table v(q, pi) v(pi, s) ed(q, s) # % <1, 0, 1> <0, 0, 1> 1 1 14 <1, 0, 1> <0, 0, 1> 2 4 57 <1, 0, 1> <0, 0, 1> 3 7 100 … … <1, 1, 0> <1, 0, 2> 3 21 25 <1, 1, 0> <1, 0, 2> 4 63 75 <1, 1, 0> <1, 0, 2> 5 84 100 … Global lookup: [<1, 1, 0>, <1, 0, 2>, 3] l Fraction is 25% x 7 = 1. 75 l Iterate through F 1, and add up contributions l … 39/68

Cons l l Hard to maintain if clusters start drifting Hard to find good number of clusters l l Space/Time tradeoffs Needs training to construct good dataset statistics table 40/68

VSol – minhash (MBKS 07) l l Solution based on minhash is used for: l l Estimate the size of a set |s| Estimate resemblance of two sets - l l I. e. , estimating the size of J=|s 1 s 2| / |s 1 s 2| Estimate the size of the union |s 1 s 2| Hence, estimating the size of the intersection - |s 1 s 2| J~(s 1, s 2) 41/68

Minhash l l Given a set s = {t 1, …, tm} Use independent hash functions h 1, …, hk: l l l hi: n-gram [0, 1] Hash elements of s, k times Keep the k elements that hashed to the smallest value each time We reduced set s, from m to k elements Denote minhash signature with s’ 42/68

How to use minhash l Given two signatures q’, s’: l J(q, s) Σ 1 i k I{q’[i]=s’[i]} / k l l l |s| ( k / Σ 1 i k s’[i] ) - 1 (q s)’ = q’ s’ = min 1 i k(q’[i], s’[i]) Hence: - |q s| (k / Σ 1 i k (q s)’[i]) - 1 43/68

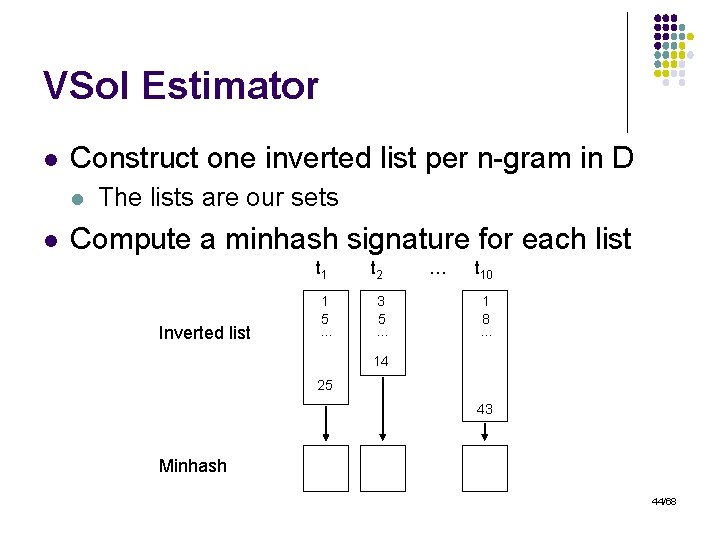
VSol Estimator l Construct one inverted list per n-gram in D l l The lists are our sets Compute a minhash signature for each list t 1 Inverted list 1 5 … t 2 3 5 … … t 10 1 8 … 14 25 43 Minhash 44/68

Selectivity Estimation l Use edit distance length filter: l l If ed(q, s) δ, then q and s share at least L = |s| - 1 - n (δ-1) n-grams Given query q = {t 1, …, tm}: l l Answer is the size of the union of all non-empty Lintersections (binomial coefficient: m choose L) We can estimate sizes of L-intersections using minhash signatures 45/68

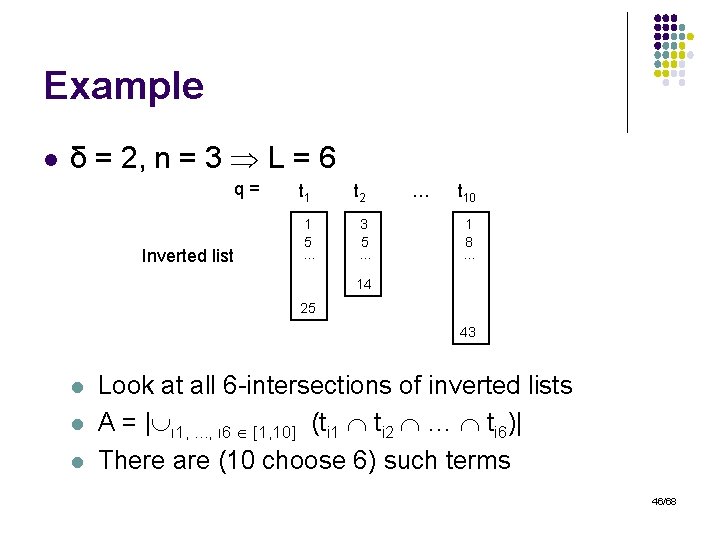
Example l δ = 2, n = 3 L = 6 q= Inverted list t 1 1 5 … t 2 3 5 … … t 10 1 8 … 14 25 43 l l l Look at all 6 -intersections of inverted lists Α = | ι 1, . . . , ι 6 [1, 10] (ti 1 ti 2 … ti 6)| There are (10 choose 6) such terms 46/68

The m-L Similarity Can be done efficiently using minhashes l Answer: l l ρ = Σ 1 j k I{ i 1, …, i. L: ti 1’[j] = … = ti. L’[j] } A ρ |t 1 … tm| Proof very similar to the proof for minhashes 47/68

Cons l Will overestimate results l l Many L-intersections will share strings Edit distance length filter is loose 48/68

Opt. EQ – wild-card n-grams (LNS 07) l Use extended n-grams: l l Introduce wild-card symbol ‘? ’ E. g. , “ab? ” can be: - l “aba”, “abb”, “abc”, … Build an extended n-gram table: l l l Extract all 1 -grams, 2 -grams, …, n-grams Generalize to extended 2 -grams, …, n-grams Maintain an extended n-grams/frequency hashtable 49/68

Example Dataset string abc def ghi … n-gram table n-gram Frequency ab 10 bc 15 de 4 ef 1 gh 21 hi 2 … … ? b 13 a? 17 ? c 23 … … abc 5 def 2 … … 50/68

Query Expansion (Replacements only) l l l Given query q=“abcd” δ=2 And replacements only: l Base strings: - l “? ? cd”, “? b? d”, “? bc? ”, “a? ? d”, “a? c? ”, “ab? ? ” Query answer: - S 1={s D: s ”? ? cd”}, S 2=… A = |S 1 S 2 S 3 S 4 S 5 S 6| = Σ 1 n 6 (-1)n-1 |S 1 … Sn| 51/68

Replacement Intersection Lattice A = Σ 1 n 6 (-1)n-1 |S 1 … Sn| l l Need to evaluate size of all 2 -intersections, 3 intersections, …, 6 -intersections Then, use n-gram table to compute sum A Exponential number of intersections But. . . there is well-defined structure 52/68

Replacement Lattice l Build replacement lattice: ? ? cd ? b? d ? bc? a? ? d a? cd ab? d a? c? ab? ? abcd l l 2 ‘? ’ 1 ‘? ’ 0 ‘? ’ Many intersections are empty Others produce the same results l we need to count everything only once 53/68

General Formulas l Similar reasoning for: l l l Other combinations difficult: l l l r replacements d deletions Multiple insertions Combinations of insertions/replacements But … we can generate the corresponding lattice algorithmically! l Expensive but possible 54/68

Basic. EQ l Partition strings by length: l l Query q with length l Possible matching strings with lengths: - l [l-δ, l+δ] For k = l-δ to l+δ - Find all combinations of i+d+r = δ and l+i-d=k If (i, d, r) is a special case use formula Else generate lattice incrementally: § § Start from query base strings (easy to generate) Begin with 2 -intersections and build from there 55/68

Opt. Eq l Details are cumbersome l l Left for homework Various optimizations possible to reduce complexity 56/68

Cons l l l Fairly complicated implementation Expensive Works for small edit distance only 57/68

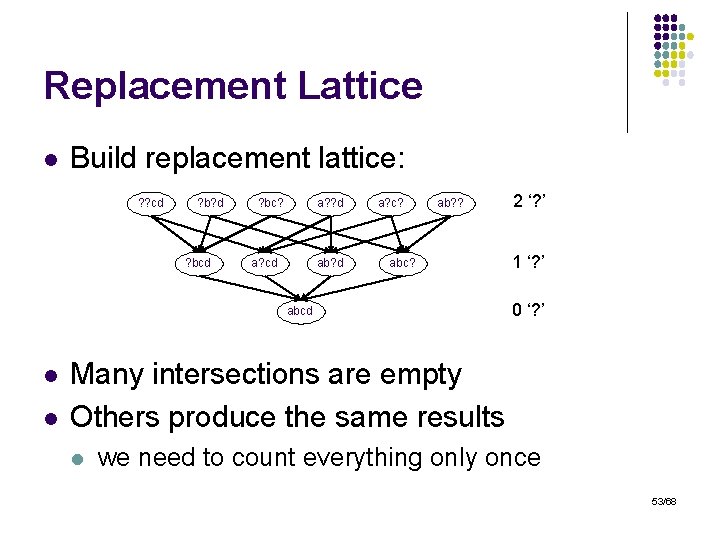
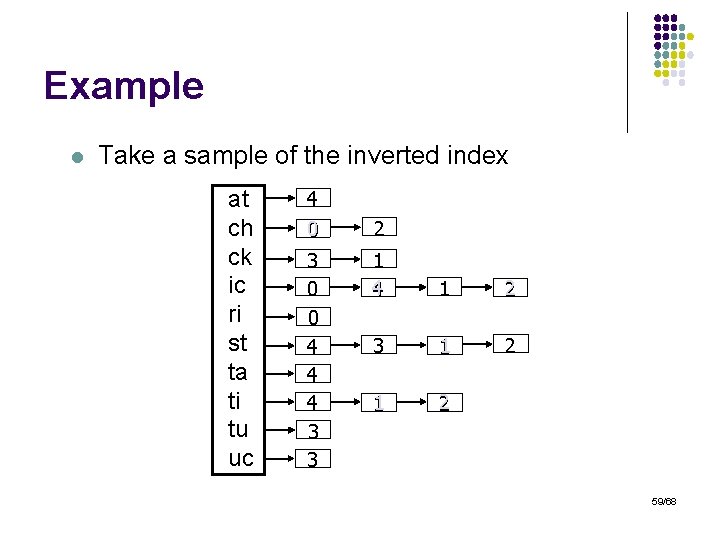
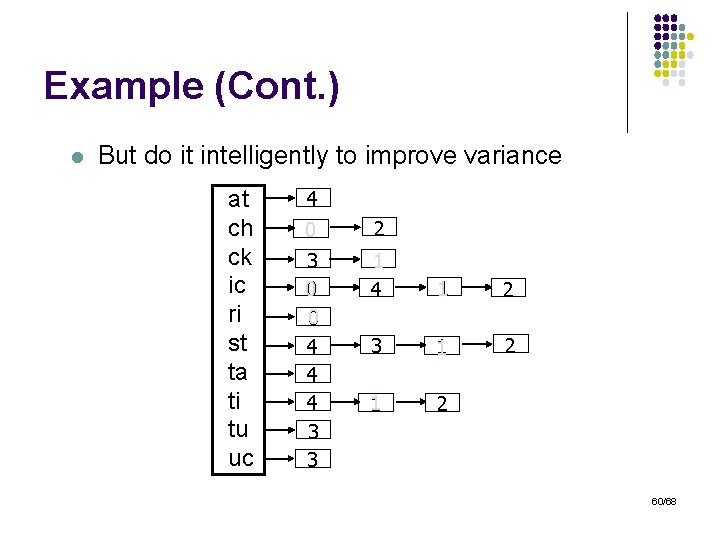
Hashed Sampling (HYKS 08) l l Used to estimate selectivity of TF/IDF, BM 25, DICE (vector space model) Main idea: l l Take a sample of the inverted index But do it intelligently to improve variance 58/68

Example l Take a sample of the inverted index at ch ck ic ri st ta ti tu uc 4 0 3 0 0 4 4 4 3 3 2 1 4 1 2 3 1 2 59/68

Example (Cont. ) l But do it intelligently to improve variance at ch ck ic ri st ta ti tu uc 4 0 2 3 0 0 4 4 4 3 3 1 4 1 2 3 1 2 60/68

Construction l Draw samples deterministically: l l l Use a hash function h: N [0, 100] Keep ids that hash to values smaller than σ Invariant: l If a given id is sampled in one list, it will always be sampled in all other lists that contain it: - S(q, s) can be computed directly from the sample No need to store complete sets in the sample No need for extra I/O to compute scores 61/68

Selectivity Estimation l l The union of arbitrary list samples is an σ% sample Given query q = {t 1, …, tm}: l A = |Aσ| |t 1 … tm| / |tσ1 … tσm|: - l Aσ is the query answer size from the sample The fraction is the actual scale-up factor But there are duplicates in these unions! We need to know: - The distinct number of ids in t 1 … tm The distinct number of ids in tσ1 … tσm 62/68

Count Distinct l Distinct |tσ1 … tσm| is easy: l l Scan the sampled lists Distinct |t 1 … tm| is hard: l l Scanning the lists is the same as computing the exact answer to the query … naively We are lucky: - - Each list sample doubles up as a k-minimum value estimator by construction! We can use the list samples to estimate the distinct |t 1 … t m| 63/68

The k-Minimum Value Synopsis l It is used to estimated the distinct size of arbitrary set unions (the same as FM sketch): l l l Take hash function h: N [0, 100] Hash each element of the set The r-th smallest hash value is an unbiased estimator of count distinct: r 0 hr hr r 100 ? 100 64/68

Outline l l l Motivation and preliminaries Inverted list based algorithms Gram signature algorithms Length normalized algorithms Selectivity estimation Conclusion and future directions 65/68

Future Directions l Result ranking l l l Diversity of query results l l l In practice need to run multiple types of searches Need to identify the “best” results Some queries have multiple meanings E. g. , “Jaguar” Updates l Incremental maintenance 66/68

References l l l [AGK 06] Arvind Arasu, Venkatesh Ganti, Raghav Kaushik: Efficient Exact Set-Similarity Joins. VLDB 2006 [BJL+09] Space-Constrained Gram-Based Indexing for Efficient Approximate String Search, Alexander Behm, Shengyue Ji, Chen Li, and Jiaheng Lu, ICDE 2009 [HCK+08] Marios Hadjieleftheriou, Amit Chandel, Nick Koudas, Divesh Srivastava: Fast Indexes and Algorithms for Set Similarity Selection Queries. ICDE 2008 [HYK+08] Marios Hadjieleftheriou, Xiaohui Yu, Nick Koudas, Divesh Srivastava: Hashed samples: selectivity estimators for set similarity selection queries. PVLDB 2008. [JL 05] Selectivity Estimation for Fuzzy String Predicates in Large Data Sets, Liang Jin, and Chen Li. VLDB 2005. [KSS 06] Record linkage: Similarity measures and algorithms. Nick Koudas, Sunita Sarawagi, and Divesh Srivastava. SIGMOD 2006. [LLL 08] Efficient Merging and Filtering Algorithms for Approximate String Searches, Chen Li, Jiaheng Lu, and Yiming Lu. ICDE 2008. [LNS 07] Hongrae Lee, Raymond T. Ng, Kyuseok Shim: Extending Q-Grams to Estimate Selectivity of String Matching with Low Edit Distance. VLDB 2007 [LWY 07] VGRAM: Improving Performance of Approximate Queries on String Collections Using Variable-Length Grams, Chen Li, Bin Wang, and Xiaochun Yang. VLDB 2007 [MBK+07] Arturas Mazeika, Michael H. Böhlen, Nick Koudas, Divesh Srivastava: Estimating the selectivity of approximate string queries. ACM TODS 2007 [XWL 08] Chuan Xiao, Wei Wang, Xuemin Lin: Ed-Join: an efficient algorithm for similarity joins with edit distance constraints. PVLDB 2008 67/68

References l l l l [XWL+08] Chuan Xiao, Wei Wang, Xuemin Lin, Jeffrey Xu Yu: Efficient similarity joins for near duplicate detection. WWW 2008. [YWL 08] Cost-Based Variable-Length-Gram Selection for String Collections to Support Approximate Queries Efficiently, Xiaochun Yang, Bin Wang, and Chen Li, SIGMOD 2008 [JLV 08]L. Jin, C. Li, R. Vernica: SEPIA: Estimating Selectivities of Approximate String Predicates in Large Databases, VLDBJ 08 [CGK 06] S. Chaudhuri, V. Ganti, R. Kaushik : A Primitive Operator for Similarity Joins in Data Cleaning, ICDE 06 [CCGX 08]K. Chakrabarti, S. Chaudhuri, V. Ganti, D. Xin: An Efficient Filter for Approximate Membership Checking, SIGMOD 08 [SK 04] Sunita Sarawagi, Alok Kirpal: Efficient set joins on similarity predicates. SIGMOD Conference 2004: 743 -754 [BK 02] Jérémy Barbay, Claire Kenyon: Adaptive intersection and t-threshold problems. SODA 2002: 390 -399 [CGG+05] Surajit Chaudhuri, Kris Ganjam, Venkatesh Ganti, Rahul Kapoor, Vivek R. Narasayya, Theo Vassilakis: Data cleaning in microsoft SQL server 2005. SIGMOD Conference 2005: 918920 68/68