Efficient and Flexible Fair Scheduling of Realtime Tasks

Efficient and Flexible Fair Scheduling of Real-time Tasks on Multiprocessors Anand Srinivasan (anands@cs. unc. edu) Department of Computer Science University of North Carolina at Chapel Hill Anand Srinivasan

What is a Real-time System? A system with a dual notion of correctness: ØLogical correctness (“it does the right thing”). ØTemporal correctness (“it does it on time”). 12/20/2021 Anand Srinivasan 2

What is a Real-time System? A system with a dual notion of correctness: ØLogical correctness (“it does the right thing”). ØTemporal correctness (“it does it on time”). Example: a robot picking up objects from a conveyor belt. 12/20/2021 Anand Srinivasan 3

Current Trends 1. Sophisticated real-time applications with high computational demands are emerging. 2. Multiprocessors are becoming extremely cost-effective. Multiprocessor real-time designs will continue to be of growing importance. 12/20/2021 Anand Srinivasan 4

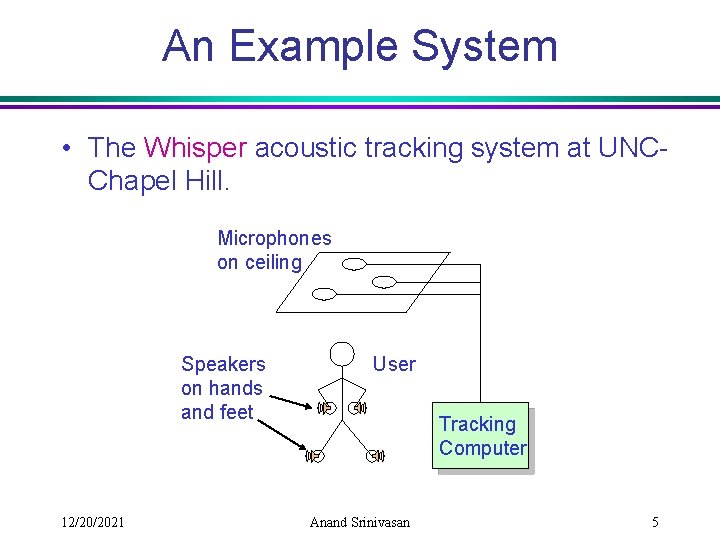
An Example System • The Whisper acoustic tracking system at UNCChapel Hill. Microphones on ceiling Speakers on hands and feet 12/20/2021 User Tracking Computer Anand Srinivasan 5

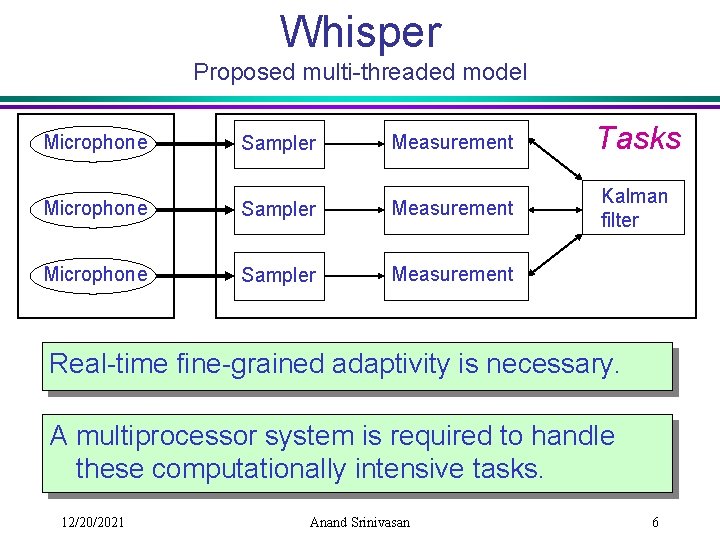
Whisper Proposed multi-threaded model Microphone Sampler Measurement Tasks Microphone Sampler Measurement Kalman filter Microphone Sampler Measurement Real-time fine-grained adaptivity is necessary. A multiprocessor system is required to handle these computationally intensive tasks. 12/20/2021 Anand Srinivasan 6

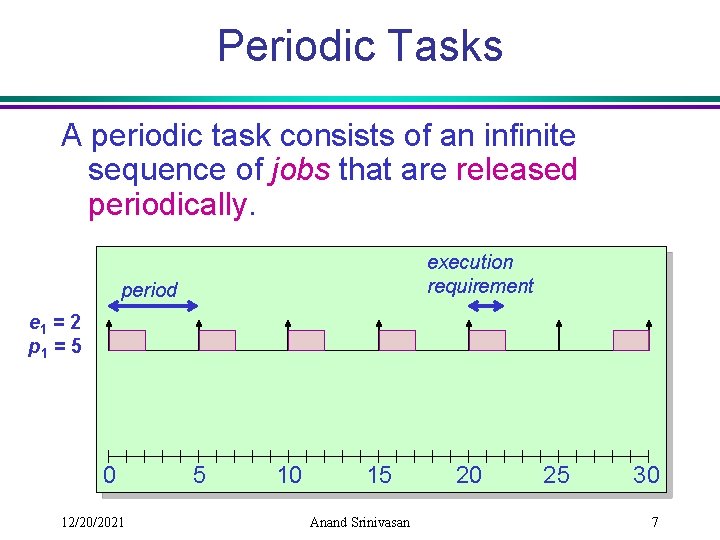
Periodic Tasks A periodic task consists of an infinite sequence of jobs that are released periodically. execution requirement period e 1 = 2 p 1 = 5 0 12/20/2021 5 10 15 Anand Srinivasan 20 25 30 7

Periodic Tasks Relative deadline of a task is equal to its period. Ø Deadline of a job equals release-time of next job of that task. e 1 = 2 p 1 = 5 e 2 = 9 p 2 = 15 0 5 10 15 20 25 30 Weight of a task with execution requirement e and period p is. 12/20/2021 Anand Srinivasan 8

Real-time Systems Need two algorithms: (i) Scheduler (typically, run-time). (ii) Schedulability test (typically, offline). Example: Scheduling periodic tasks on a uniprocessor. (i) Scheduler is earliest-deadline-first (EDF). (ii) Schedulability test is “ ”. Set of tasks 12/20/2021 Yes Run the system with EDF No Re-design the system Anand Srinivasan 9

Overview • Fair scheduling on multiprocessors Ø Efficiency: The PD 2 scheduling algorithm Ø Experimental comparison with other approaches • Flexibility Ø Dynamic task systems Ø Rate-based scheduling on multiprocessors • Summary 12/20/2021 Anand Srinivasan 10

Overview • Fair scheduling on multiprocessors Ø Efficiency: The PD 2 scheduling algorithm Ø Experimental comparison with other approaches • Flexibility Ø Dynamic task systems Ø Rate-based scheduling on multiprocessors • Summary 12/20/2021 Anand Srinivasan 11

Scheduling Problem Given a set of n periodic tasks to be scheduled on m (< n) processors. ØDetermine whether they can be correctly scheduled. ØWhich scheduling approach and algorithm should we use? 12/20/2021 Anand Srinivasan 12

Assumptions • Periods and worst-case execution requirements are given. ØAll values are integral. • All processors are identical and main memory is shared. • Preemptions and inter-processor migrations are allowed, but parallelism is not. • No context switch and migration overhead. ØThese are accounted for in the worst-case execution times of the tasks. 12/20/2021 Anand Srinivasan 13

Feasibility and Optimality [Baruah et al. ] A periodic task set is feasible on m processors iff weight(T) ≤ m. A scheduling algorithm is said to be optimal if it can correctly schedule any feasible task set. 12/20/2021 Anand Srinivasan 14

Proportionate Fair Scheduling [Baruah et al. ] • Scheduling decisions are based on the behavior of an ideal fluid system. TIME A weight = 2/5 B weight = 3/5 0 5 2/5 3/5 10 Ideal schedule Quantum-based schedule A Pfair schedule is a quantum-based schedule in which tasks are allocated fairly in proportion to their weights. 12/20/2021 Anand Srinivasan 15

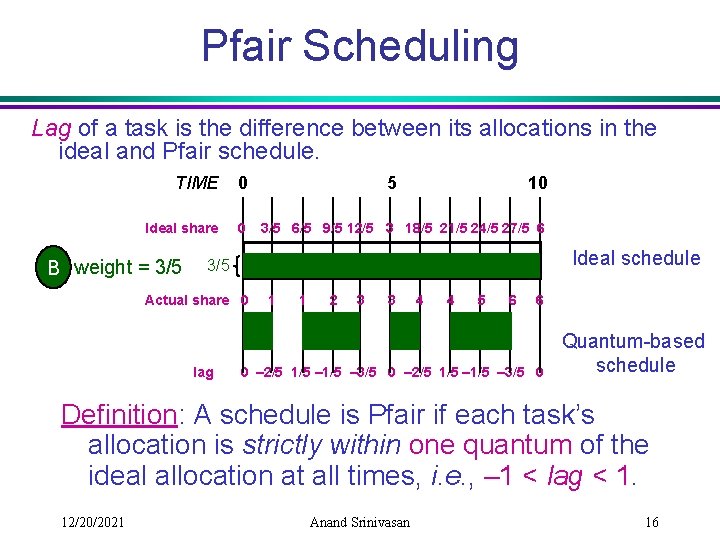
Pfair Scheduling Lag of a task is the difference between its allocations in the ideal and Pfair schedule. TIME 0 Ideal share 0 B weight = 3/5 5 10 3/5 6/5 9/5 12/5 3 18/5 21/5 24/5 27/5 6 Ideal schedule 3/5 Actual share 0 lag 1 1 2 3 3 4 4 5 6 6 0 – 2/5 1/5 – 3/5 0 Quantum-based schedule Definition: A schedule is Pfair if each task’s allocation is strictly within one quantum of the ideal allocation at all times, i. e. , – 1 < lag < 1. 12/20/2021 Anand Srinivasan 16

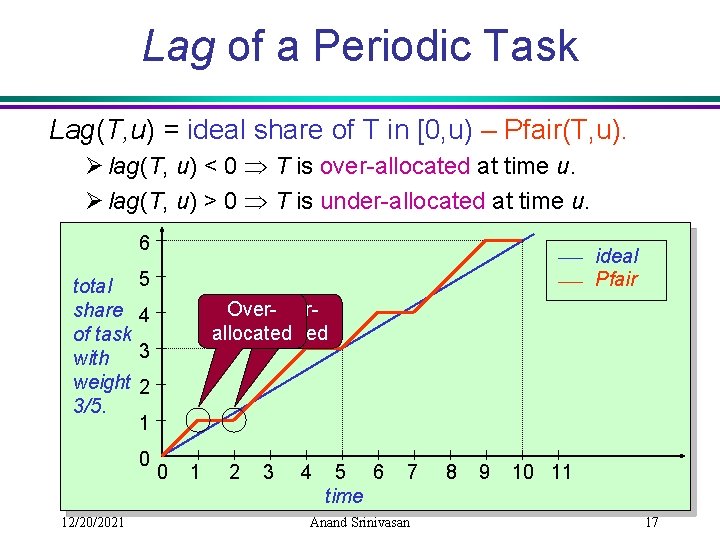
Lag of a Periodic Task Lag(T, u) = ideal share of T in [0, u) – Pfair(T, u). Ø lag(T, u) < 0 T is over-allocated at time u. Ø lag(T, u) > 0 T is under-allocated at time u. 6 total share of task with weight 3/5. 5 Over. Underallocated 4 3 2 1 0 12/20/2021 ideal Pfair 0 1 2 3 4 5 6 time 7 Anand Srinivasan 8 9 10 11 17

Scheduling of Periodic Tasks • Share of T in ideal schedule in [0, u) = ( • lag(T, u) = ) u. – Pfair(T, u). • If p divides u, then lag is an integer. – 1< lag < 1 lag = 0. Hence, all jobs meet their deadlines. 12/20/2021 Anand Srinivasan 18

Scheduling of Subtasks Each task is effectively divided into a series of quantum-length subtasks. TIME Consider a task T of weight 3/7. 1 2 3 4 5 6 7 Subtask 3 lag = 9/7 Subtask 2 Subtask 1 lag(T, 3) = (3/7) 3 – 0 = 9/7 > 1 So the first subtask must finish by time 3. 12/20/2021 Anand Srinivasan 19

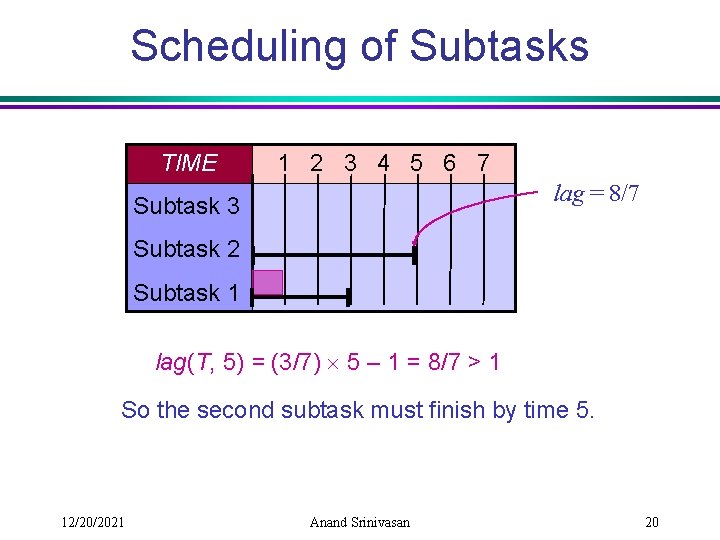
Scheduling of Subtasks TIME 1 2 3 4 5 6 7 lag = 8/7 Subtask 3 Subtask 2 Subtask 1 lag(T, 5) = (3/7) 5 – 1 = 8/7 > 1 So the second subtask must finish by time 5. 12/20/2021 Anand Srinivasan 20

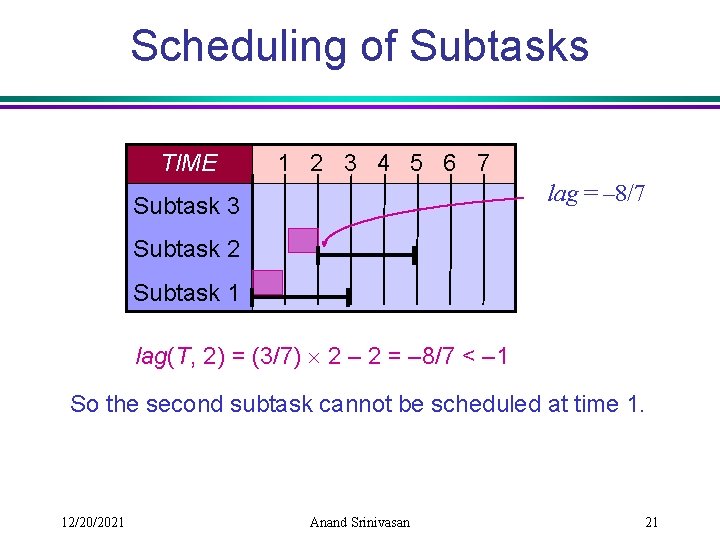
Scheduling of Subtasks TIME 1 2 3 4 5 6 7 lag = – 8/7 Subtask 3 Subtask 2 Subtask 1 lag(T, 2) = (3/7) 2 – 2 = – 8/7 < – 1 So the second subtask cannot be scheduled at time 1. 12/20/2021 Anand Srinivasan 21

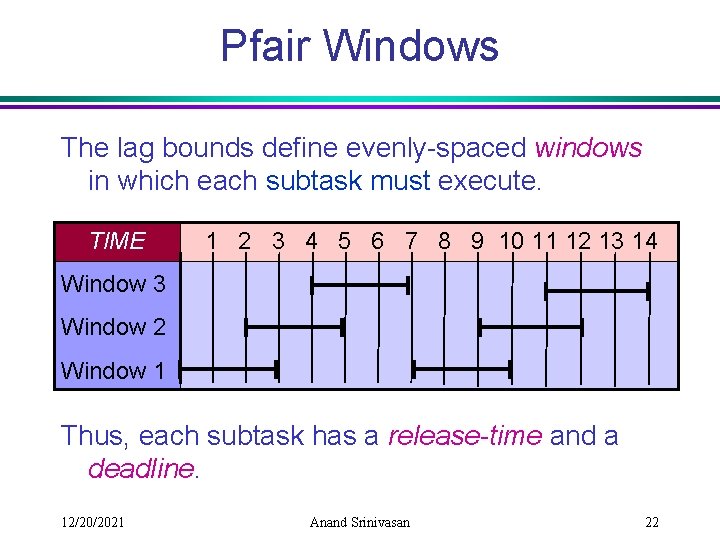
Pfair Windows The lag bounds define evenly-spaced windows in which each subtask must execute. TIME 1 2 3 4 5 6 7 8 9 10 11 12 13 14 Window 3 Window 2 Window 1 Thus, each subtask has a release-time and a deadline. 12/20/2021 Anand Srinivasan 22

Optimal Pfair Schedulers PF, PD, and PD 2. ØInvoked at the beginning of each quantum. v. Select m highest-priority subtasks for execution. ØUse deadlines of subtasks to determine priority. ØBased on EDF. v. Differ in the choice of tie-breaking rules. Tie-breaking rules are necessary for optimality on more than three processors. 12/20/2021 Anand Srinivasan 23

The PF Scheduling Algorithm PF [Baruah et al. 1993] T T has higher priority at time t … U t 12/20/2021 Anand Srinivasan 24

PF Swapping Proof Proved optimal by an inductive swapping proof: Transform a correct schedule into a PF schedule. Consider a two-processor schedule. T … U 12/20/2021 Anand Srinivasan 25

The PD Scheduling Algorithm [Baruah et al. 1995] • Uses four tie-breaking rules (applied in sequence). ØAny further ties can be broken arbitrarily. • Polynomial time: O (m log n). Øm processors, n tasks. • Proved to be optimal by showing that PD “closely” tracks PF. 12/20/2021 Anand Srinivasan 26

The PD 2 Scheduling Algorithm [Anderson and Srinivasan, 2000] • Uses only two tie-breaking rules. • Polynomial time: O (m log n). Øm processors, n tasks. • Optimality proved by a swapping proof. ØMuch more complicated than the proof for PF. 12/20/2021 Anand Srinivasan 27

Results about PD 2 • Most efficient among all known Pfair scheduling algorithms that are optimal. ØIf any of the tie-breaking rules is eliminated, task sets exist that miss deadlines. • For systems consisting of tasks with weight at most ½, only one tie-breaking rule is necessary. • For two-processor systems, no tiebreaking rules are required. James H. Anderson and Anand Srinivasan, Early-release Fair Scheduling, IEEE Euromicro Conference on Real-time Systems, 2000. 12/20/2021 Anand Srinivasan 28

Overview • Fair scheduling on multiprocessors Ø Efficiency: The PD 2 scheduling algorithm Ø Experimental comparison with other approaches • Flexibility Ø Dynamic task systems Ø Rate-based scheduling on multiprocessors • Summary 12/20/2021 Anand Srinivasan 29

Comparison with Partitioning Approaches Partition the set of tasks so that each task always runs on the same processor. Steps: 1. Choose a uniprocessor scheduling algorithm. 2. Use the corresponding uniprocessor schedulability test to determine the partitions. 12/20/2021 Anand Srinivasan 30

Partitioning Approaches • Disadvantages: ØInherently sub-optimal. v. Consider a two-processor system with three tasks of weight 2/3 (= 0. 66) each. ØBin-packing is NP-hard in the strong sense. • Advantages: ØUniprocessor algorithms can be used. ØNo migration overhead is incurred. ØIt performs well in practice. 12/20/2021 Anand Srinivasan 31

Experimental Setup [Srinivasan et al. ] • Overheads: Ø Scheduling overheads. Ø Context-switch cost (= 5μs). Ø Cache-related preemption delay ( [0, 100μs]). • Approach: Ø Generate random periodic task sets with a given total utilization. Ø Calculate new worst-case execution times after incorporating the above overheads. Ø Determine the minimum number of processors required by PD 2 and EDF with First-Fit. v. First-fit: Each task is assigned to the first processor that can accept it. 12/20/2021 Anand Srinivasan 32

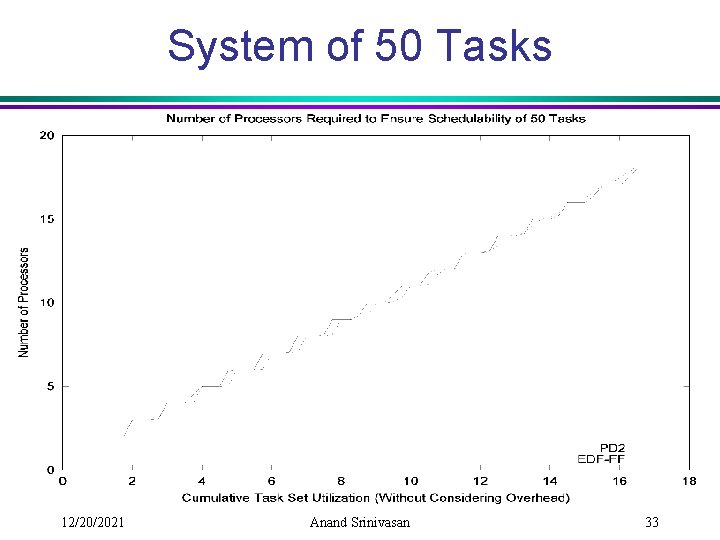
System of 50 Tasks 12/20/2021 Anand Srinivasan 33

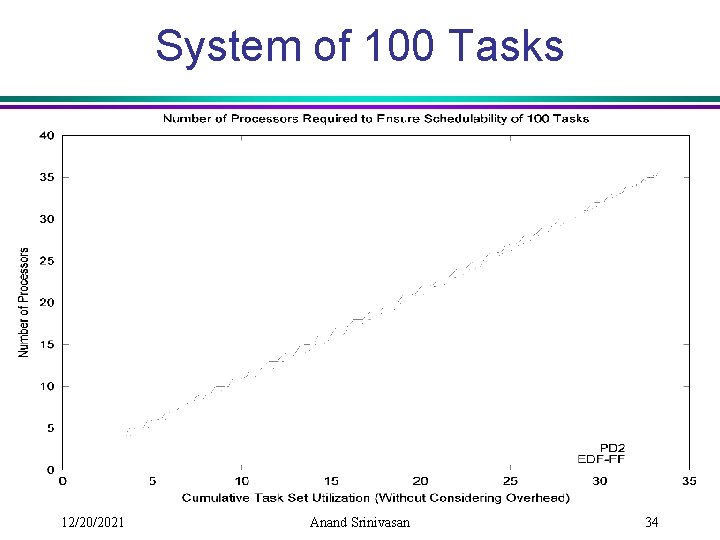
System of 100 Tasks 12/20/2021 Anand Srinivasan 34

Why use PD 2? • PD 2 gives almost same performance as EDF with First-Fit under all cases. • Efficiently supporting critical sections is difficult with partitioning. ØEfficient schemes have been presented for PD 2 by Holman and Anderson [2002, 2003]. • Partitioning is not suitable for highlydynamic task systems. 12/20/2021 Anand Srinivasan 35

Overview • Fair scheduling on multiprocessors Ø Efficiency: The PD 2 scheduling algorithm Ø Experimental comparison with other approaches • Flexibility Ø Dynamic task systems Ø Rate-based scheduling on multiprocessors • Summary 12/20/2021 Anand Srinivasan 36

Dynamic Task Systems Whisper re-visited Features of Whisper: ØReal-time guarantees are required to ensure high fidelity response. ØMultiprocessor system is required to handle computational demands. ØHighly-dynamic system: Fine-grained adaptive nature implies that computational demands vary over time. 12/20/2021 Anand Srinivasan 37

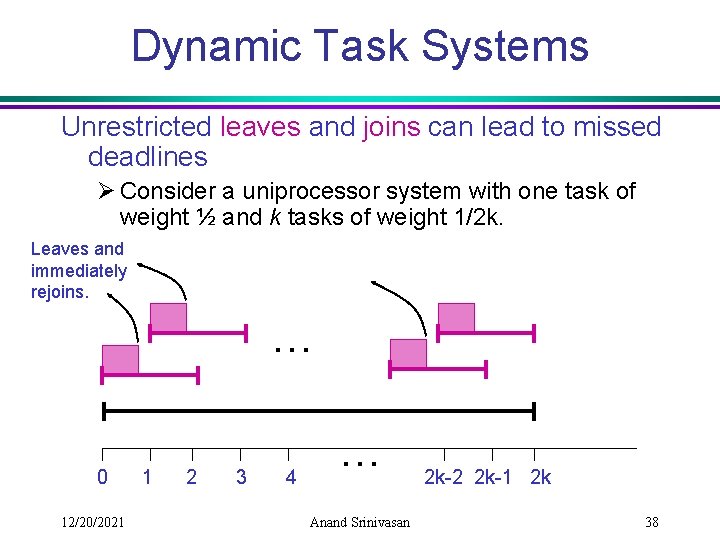
Dynamic Task Systems Unrestricted leaves and joins can lead to missed deadlines Ø Consider a uniprocessor system with one task of weight ½ and k tasks of weight 1/2 k. Leaves and immediately rejoins. … 0 12/20/2021 1 2 3 4 … Anand Srinivasan 2 k-2 2 k-1 2 k 38

Dynamic Task Systems Join condition: Check feasibility with the new task. Leave condition (trickier): Allow task to leave only if it is not over-allocated, i. e. , lag 0. Ø This is sufficient on uniprocessors [Stoica et al. 1996] Ø This is not sufficient, in general, on multiprocessors. It is sufficient if the final job executes for its worst-case execution time. Ø We have also provided tighter conditions under which tasks are allowed to leave earlier. Anand Srinivasan and James H. Anderson, Fair scheduling of dynamic task systems on multiprocessors, WPDRTS, 2003. 12/20/2021 Anand Srinivasan 39

Overview • Fair scheduling on multiprocessors Ø Efficiency: The PD 2 scheduling algorithm Ø Experimental comparison with other approaches • Flexibility Ø Dynamic task systems Ø Rate-based scheduling on multiprocessors • Summary 12/20/2021 Anand Srinivasan 40

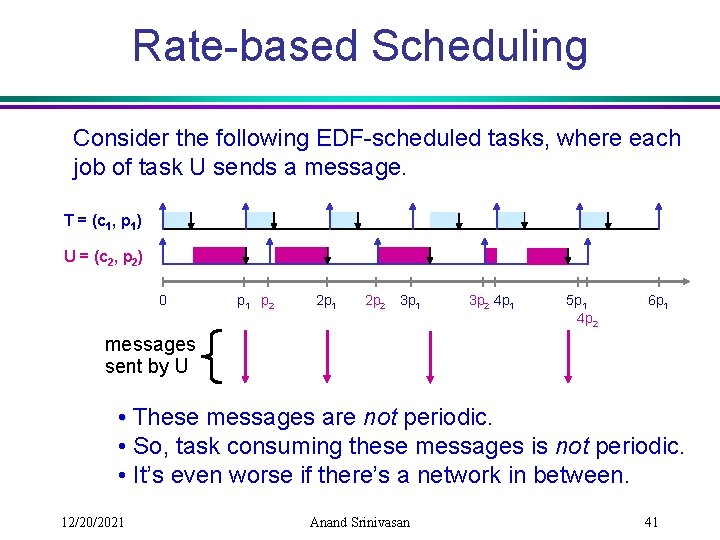
Rate-based Scheduling Consider the following EDF-scheduled tasks, where each job of task U sends a message. T = (c 1, p 1) U = (c 2, p 2) 0 p 1 p 2 2 p 1 2 p 2 3 p 1 3 p 2 4 p 1 5 p 1 4 p 2 6 p 1 messages sent by U • These messages are not periodic. • So, task consuming these messages is not periodic. • It’s even worse if there’s a network in between. 12/20/2021 Anand Srinivasan 41

Intra-sporadic (IS) Tasks • The IS model allows subtasks to be released late, i. e. , separation between consecutive subtask releases may be more than that for a periodic task. • In addition to release and deadline, each subtask Ti has an eligibility time, which may be less than its release time. 12/20/2021 Anand Srinivasan 42

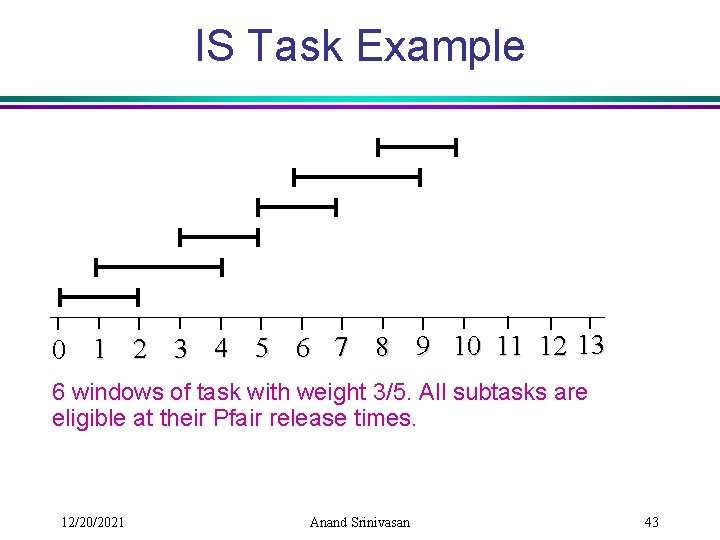
IS Task Example 0 1 2 3 4 5 6 7 8 9 10 11 12 13 6 windows of task with weight 3/5. All subtasks are eligible at their Pfair release times. 12/20/2021 Anand Srinivasan 43

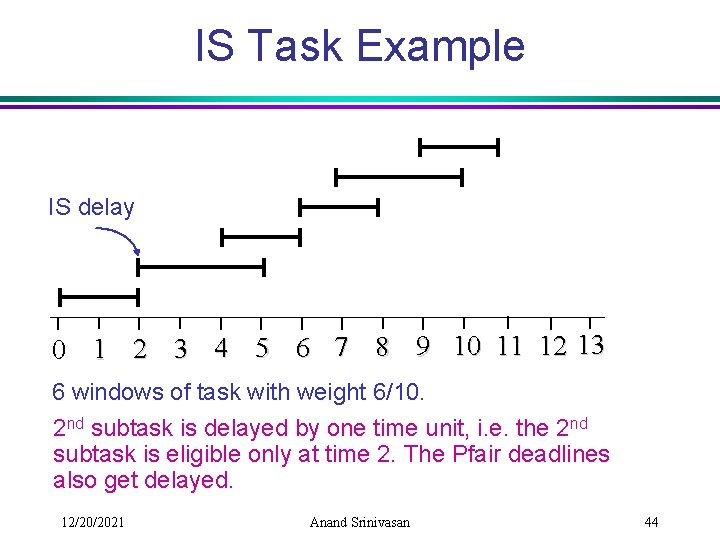
IS Task Example IS delay 0 1 2 3 4 5 6 7 8 9 10 11 12 13 6 windows of task with weight 6/10. 2 nd subtask is delayed by one time unit, i. e. the 2 nd subtask is eligible only at time 2. The Pfair deadlines also get delayed. 12/20/2021 Anand Srinivasan 44

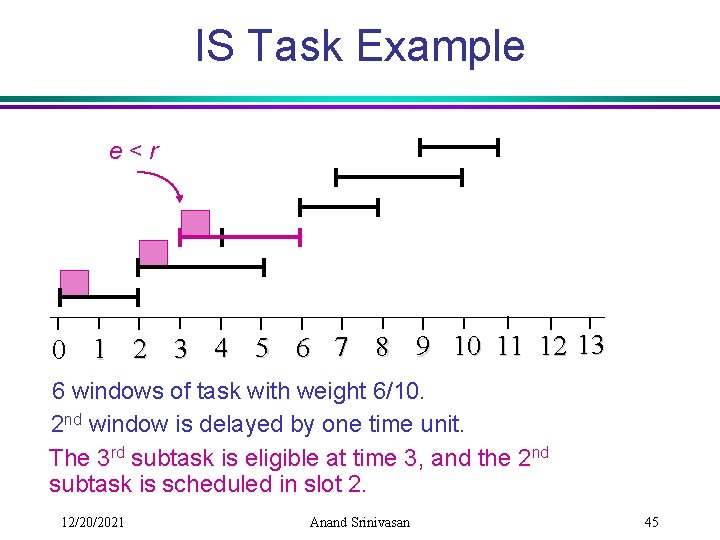
IS Task Example e<r 0 1 2 3 4 5 6 7 8 9 10 11 12 13 6 windows of task with weight 6/10. 2 nd window is delayed by one time unit. The 3 rd subtask is eligible at time 3, and the 2 nd subtask is scheduled in slot 2. 12/20/2021 Anand Srinivasan 45

Other Example Applications • Multimedia application: ØConsider an application receiving packets over a network. v. Packets arrive in bursts. v. Possible delay sometimes. • Tasks that self-suspend (for example, due to RPC, I/O). • Tasks that block (for example, due to locks). 12/20/2021 Anand Srinivasan 46

Results about IS tasks Feasibility: An intra-sporadic task system is feasible on m processors iff weight(T) ≤ m. PD 2 is optimal on any number of processors. Ø No tie-breaks are necessary on two processors. Ø No tie-breaks are necessary on three processors if all tasks have weight at most ½. Anand Srinivasan and James H. Anderson, Optimal Rate-based Scheduling on Multiprocessors, STOC, 2002. 12/20/2021 Anand Srinivasan 47

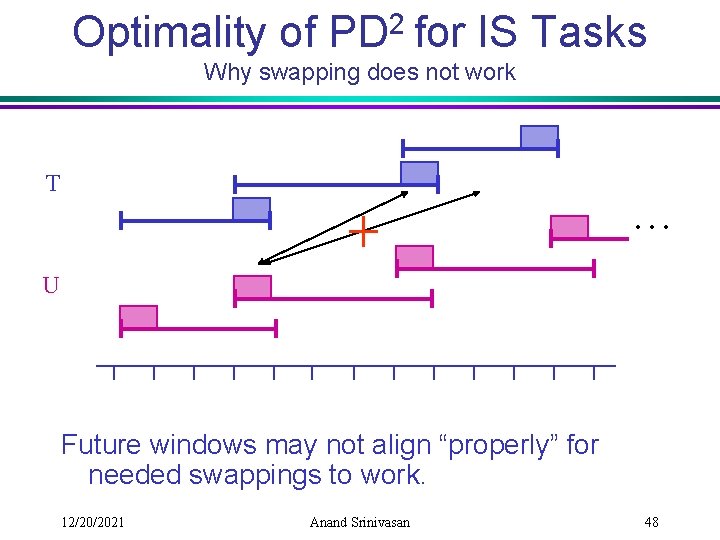
Optimality of PD 2 for IS Tasks Why swapping does not work T … U Future windows may not align “properly” for needed swappings to work. 12/20/2021 Anand Srinivasan 48

Overview • Fair scheduling Ø Efficiency: The PD 2 scheduling algorithm Ø Experimental comparison with other approaches • Flexibility Ø Dynamic task systems Ø Rate-based scheduling on multiprocessors • Summary 12/20/2021 Anand Srinivasan 49

Summary of Contributions • This talk: Ø The PD 2 Pfair scheduling algorithm. Ø Dynamic real-time multiprocessor systems. Ø Rate-based scheduling on multiprocessors. • Other work: Ø Soft real-time multiprocessor systems. vin submission. Ø Scheduling of packet processing activities on a network processor. v. Workshop on Network Processors 2003. Ø Scheduling of aperiodic tasks. v. Euromicro Conference in Real-time Systems 2002. Papers are available at http: //www. cs. unc. edu/~anands/papers. html. 12/20/2021 Anand Srinivasan 50

Future Vision Highly-dynamic and computation-intensive realtime applications are becoming increasingly common and important. Ø Automatic tracking systems. Ø Telepresence systems. Ø Processing data in disaster recovery and battlefield situations. Long term goal: Design and develop a general framework that can efficiently support such applications. 12/20/2021 Anand Srinivasan 51

Short-term Plans • Multiprocessor scheduling issues in general-purpose operating systems. ØSupport for soft real-time applications • Quality-of-service (Qo. S) Guarantees in Networking: ØDifferent set of constraints. ØIntelligent use of spare bandwidth. 12/20/2021 Anand Srinivasan 52

This slide is intentionally left blank! 12/20/2021 Anand Srinivasan 53

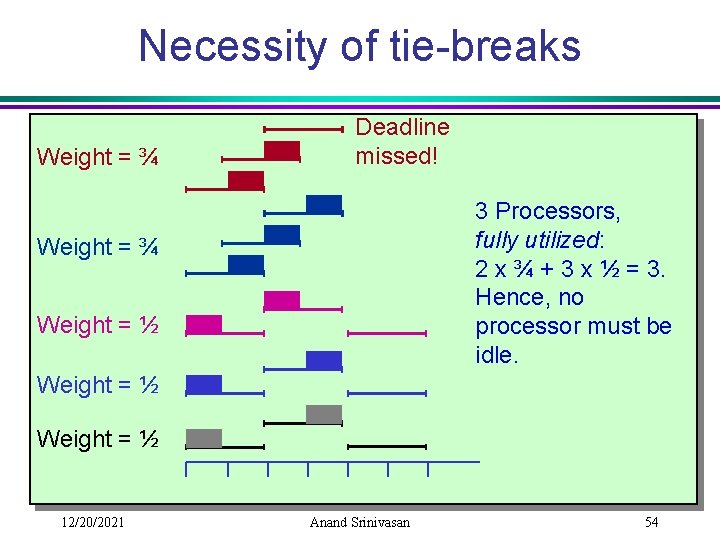
Necessity of tie-breaks Weight = ¾ Deadline missed! 3 Processors, fully utilized: 2 x ¾ + 3 x ½ = 3. Hence, no processor must be idle. Weight = ¾ Weight = ½ 12/20/2021 Anand Srinivasan 54