Efficiency of Algorithms 1 Efficiency of Algorithms Two

Efficiency of Algorithms 1

Efficiency of Algorithms Ø Two main issues related to the efficiency of algorithms: Speed of algorithm Efficient memory allocation Ø We will focus on the speed of algorithms. The speed of an algorithm (running time) is determined by the number of elementary operations: addition, subtraction, multiplication, division, comparison. The number of elementary operations depends on problem size nature of input data 2

Analysis of Running Time Ø Running time of an algorithm is a function of input size. Ø Two kind of analyses of running time: Worst-case running time analysis Average-case running time analysis Most results in the analysis of algorithms concern the worst-case running time. 3

Efficiency of Algorithms: Example Ø Recall the Traveling Salesman Problem (TSP): There are n cities. The salesman starts his tour from City 1, visits each of the cities exactly once, and returns to City 1. For each pair of cities i, j there is a cost cij associated with traveling from City i to City j. • Goal: Find a minimum-cost tour. 4

“Exhaustive enumeration” algorithm Ø One way of solving the problem is by an algorithm which is based on exhaustive enumeration (brute force): 1) Compute the costs of all possible tours; 2) Choose the tour with minimum cost. Ø What is the running time of this algorithm? 1) The number of possible tours is (n-1)! The cost of each tour is the sum of n individual costs requires n-1 additions. Thus, computing the costs of all possible tours requires (n-1)∙(n-1)! elementary operations. 2) Choosing the tour with minimum cost requires (n-1)!-1 comparisons. Summarizing, (n-1)∙(n-1)! + (n-1)! -1 = n! -1 elementary operations are needed for implementing the algorithm. 5

Efficiency of the “Exhaustive enumeration” algorithm • Is the “exhaustive enumeration” algorithm efficient? Assume that each elementary operation can be done in 1 nanosecond = 10 -9 seconds. Then the running time: n=10 n=20 n=30 0. 004 sec 77 years 8. 4 1013 centuries 6

“Nearest neighbor” algorithm Ø Consider another method for solving the TSP, the “Nearest neighbor” algorithm: In every iteration (except the last one) go to the closest city not visited yet. Ø What is the running time of this algorithm? In each iteration we choose one of the n cities; so there are n iterations. In each iteration, we need at most n comparisons to choose the next city. Thus, the total number of elementary operations is at most n 2. 7

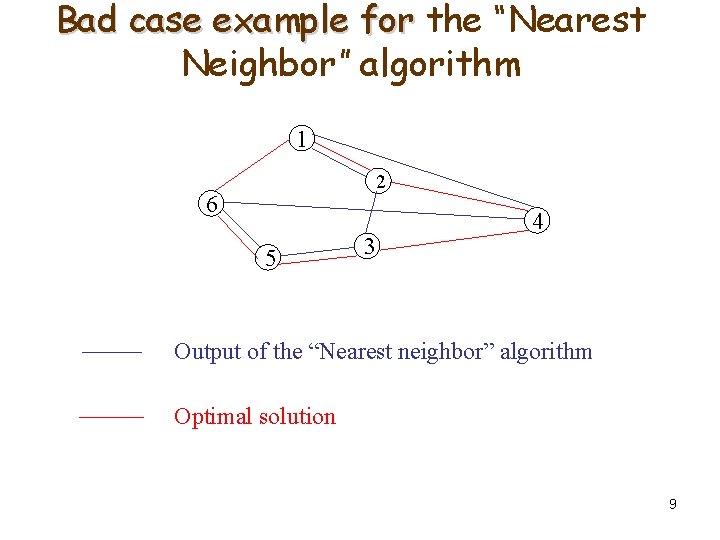
Efficiency of the “Nearest Neighbor” algorithm Compare the running times of “Nearest neighbor” and “Exhaustive enumeration” algorithms: n 2 n=10 10 -7 sec. n=30 10 -6 sec. n=100 10 -5 sec. n=1000 10 -3 sec. n! 0. 004 sec 8. 4 1013 cent. Note: The “Nearest Neighbor” algorithm might not return 8 an optimal solution.

Bad case example for the “Nearest Neighbor” algorithm 1 2 6 5 3 4 Output of the “Nearest neighbor” algorithm Optimal solution 9

Overwhelming terms in running times • Suppose in the “Exhaustive enumeration” algorithm, we need to preprocess the costs before applying the main routine (e. g. , converting kilometers to miles). • Preprocessing requires at most n 2 multiplications; thus, the running time of the new algorithm is n!+n 2. • For large n, the term n! overwhelms the term n 2. Thus, the running time n!+n 2 qualitatively is not much different from n!. 10

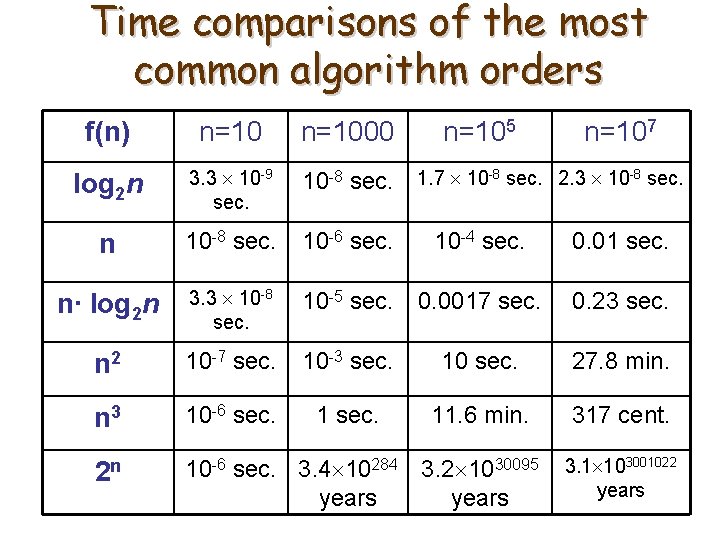
Order of an Algorithm Ø Definition: Let A be an algorithm. Let w(n) be the maximum number of elementary operations required to execute A for all possible input sets of size n. If w(n) is O(f(n)) , we say that A has a (worst case) order of f(n). Ø Ex. : Suppose the maximum number of operations needed to execute algorithm A is 5 n 2+3 n+7. Then A has an order of n 2. Ø Definition: An algorithm is called polynomial-time if it has an order of f(n)=nk for some constant k. Ø Polynomial-time algorithms are normally considered efficient. 11

Time comparisons of the most common algorithm orders f(n) n=1000 n=105 n=107 log 2 n 3. 3 10 -9 sec. 10 -8 sec. 1. 7 10 -8 sec. 2. 3 10 -8 sec. n 10 -8 sec. 10 -6 sec. 10 -4 sec. 0. 01 sec. n∙ log 2 n 3. 3 10 -8 sec. 10 -5 sec. 0. 0017 sec. 0. 23 sec. n 2 10 -7 sec. 10 -3 sec. 10 sec. 27. 8 min. n 3 10 -6 sec. 11. 6 min. 317 cent. 2 n 10 -6 sec. 3. 4 10284 3. 2 1030095 years 3. 1 103001022 years