Effects of Inflation on time value of money

REMINDER…… Test 2 – 13 December 2016. PM Dr. Mohd Najmuddin bin Mohd Hassan

LEARNING OUTCOMES 1. Understand inflation 2. Calculate PW of cash flows with inflation 3.

Understanding Inflation: Increase in amount of money needed to purchase same amount of goods

1 -5 © 2012 by Mc. Graw-Hill, New York, N. Y All Rights Reserved

Constant Value Dollar An adjusted value of currency used to compare dollar values from

Money Time Value due to the Inflation Money in one period of time t

If f is the inflation rate period, and n is the number of period

1 -9 © 2012 by Mc. Graw-Hill, New York, N. Y All Rights Reserved

Two ways to work problems when considering inflation: (1) Convert to constant value (CV)

Example: Constant Value Dollars How much would be required today to purchase an item

Three Different Rates ► Real or interest rate i = Rate at which interest

Example: Market vs. Real Rate Money in a medium-risk investment makes a guaranteed 8%

PW Calculations with Inflation Two ways to account for inflation in PW calculations (1)

Example: PW with Inflation A honing machine will have a cost of $25, 000

FW Calculations with Inflation FW values can have four different interpretations (1) The actual

Example: FW with Inflation An engineer invests $15, 000 in a savings account that

Example: FW with Inflation (b) To find the purchasing power of the accumulated amount

Capital Recovery with Inflation The A/P and A/F factors require the use of if

750, 000 1 500, 000 2 untung balik modal 3 4 i = r

Summary of Important Points Inflation occurs because value of currency has changed Inflation reduces

Problem 5. 1 An engineer is considering two types of diffusion furnaces, small (S)

Problem 5. 2 Harmony Corporation plans to set aside RM 60, 000 per year

Slides: 23

Download presentation

LEARNING OUTCOMES 1. Understand inflation 2. Calculate PW of cash flows with inflation 3. Calculate FW with inflation considered 4. Calculate AW with inflation considered 14 -3 © 2012 by Mc. Graw-Hill All Rights Reserved

Understanding Inflation: Increase in amount of money needed to purchase same amount of goods or services. Inflation results in a decrease in purchasing power, i. e. , one unit of money buys less goods or services • Occurs because the change in the value of money • As the value of money decreases, it takes more money for the same amount of goods or services. 14 -4 © 2012 by Mc. Graw-Hill All Rights Reserved

Constant Value Dollar An adjusted value of currency used to compare dollar values from one period to another. Due to inflation, the purchasing power of the dollar changes over time, so in order to compare dollar values from one year to another, they need to be converted from nominal (current) dollar values to constant dollar values. Constant dollar value may also be referred to as real dollar value or today’s dollar (present dollar). 1 -6 © 2012 by Mc. Graw-Hill, New York, N. Y All Rights Reserved

Money Time Value due to the Inflation Money in one period of time t 1, can be brought to the same value as money in another period of time t 2 by using; Lets use dollar as the currency. Dollars in period t 1 are called constant value dollar (present dollar). Dollars in period t 2 are called future dollars which have taken inflation into account. 1 -7 © 2012 by Mc. Graw-Hill, New York, N. Y All Rights Reserved

Two ways to work problems when considering inflation: (1) Convert to constant value (CV) dollars, then use real rate i. Constant-value dollars = future dollars = then. Ifcurrent f = inflation rate (% per year), the equation is: dollars (1+ f)n (1+ n (2) Leavef) money amounts as is and use interest rate adjusted for inflation, if if = i + f + (i)(f) 14 -10 © 2012 by Mc. Graw-Hill All Rights Reserved

Example: Constant Value Dollars How much would be required today to purchase an item that increased in cost by exactly the inflation rate? The cost 30 years ago was $1000 and inflation has consistently averaged 4% per year. Solution: Solve for future dollars Future dollars = constant value dollars(1 + f)n = 1000(1 + 0. 04)30 Note: This calculation only accounts = $3243 for the decreased purchasing power of the currency. It does not take into account the time value of money Deflation: Opposite of inflation; purchasing power of money (to be discussed) is greater in future than at present; however, money, credit, © 2012 by Mc. Graw-Hill All Rights Reserved 14 -11 jobs are ‘tighter’

Three Different Rates ► Real or interest rate i = Rate at which interest is earned when effects of inflation are removed; i represents the real increase in purchasing power ► Market or inflation-adjusted rate if = Rate that takes inflation into account. Commonly stated rate everyday ► Inflation rate f = Rate of change in value of currency Relation between three rates is derived using the relation Market rate is: 14 -12 © 2012 by Mc. Graw-Hill Reserved if = i + f + (i)(f) All Rights

Example: Market vs. Real Rate Money in a medium-risk investment makes a guaranteed 8% per year. Inflation rate has averaged 5. 5% per year. What is the real rate of return on the investment? (in percentage) Solution: Solve for the real rate i in relation for if i= if = i + f + (i)(f) if – f = 1+f = 0. 08 – 0. 055 1 + 0. 055 14 -13 0. 024 © 2012 by Mc. Graw-Hill Reserved All Rights

PW Calculations with Inflation Two ways to account for inflation in PW calculations (1) Convert cash flow into constant-value (CV) dollars and use r where: CV = future dollars/(1 + f)n = then-current dollars/( f = inflation rate (Note: Calculations up to now have assumed constant-value dollars) (2) Express cash flow in future (then-current ) dollars and use in interest rate where if = i + f + (i)(f) ( Note: Inflated interest rate is the market interest rate) 14 -14 © 2012 by Mc. Graw-Hill All Rights Reserved

Example: PW with Inflation A honing machine will have a cost of $25, 000 (future cost) six years from now. Find the PW of the machine, if the real interest rate is 10% per year and the inflation rate is 5% per year using (a) constant-value dollars, and (b) future dollars. Solution: (a Determine constant-value dollars and use i in PW equ CV = 25, 000 / (1 + 0. 05)6 = $18, 655 PW = 18, 655(P/F, 10%, 6) = $10, 530 (b) Leave as future dollars and use if in PW equation if = 0. 10 + 0. 05 + (0. 10)(0. 05) = 15. 5% PW = 25, 000(P/F, 15. 5%, 6) = $10, 530 14 -15 © 2012 by Mc. Graw-Hill All Rights Reserved

FW Calculations with Inflation FW values can have four different interpretations (1) The actual amount accumulated ü Use if in FW equation FW = PW(F/P, if, n) (2) The purchasing power in terms of CV dollars of the future amoun ü Use if in FW equation and divide by (1+f)n or use real i where real i = (if – f)/(1 + f) FW = PW(F/P, i, n (3) The number of future dollars required to have the same purchasing power a dollar of today withfactor no time value. FW of money ü Useasf instead i in F/P = PW(F/P, f, n) considered (4) The amount required to maintain the purchasing power of the present sum andi earn a equation stated real rate of return ü Use in FW FW f 14 -16 = PW(F/P, if, n) © 2012 by Mc. Graw-Hill All Rights Reserved

Example: FW with Inflation An engineer invests $15, 000 in a savings account that pays interes real 8% per year. If the inflation rate is 5% per year, determine (a) t of money that will be accumulated in 10 years, (b) the purchasing p the accumulated amount (in terms of today’s dollars), (c) the numb future dollars that will have the same purchasing power as the $15, 000 today, and (d) the amount to maintain purchasing power an real 8% per year return. Solution: (a) The amount accumulated is a function of the market interest ra if = 0. 08 + 0. 05 + (0. 08)(0. 05) = 13. 4% Amount Accumulated = 15, 000(F/P, 13. 4%, 10) = $52, 750 14 -17 © 2012 by Mc. Graw-Hill All Rights Reserved

Example: FW with Inflation (b) To find the purchasing power of the accumulated amount (cont’d) deflate the inflated dollars Purchasing power = 15, 000(F/P, 13. 4%, 10) / (1 + 0. 05)10 $32, 384 (c) The number of future=dollars required to purchase goods that cost $15, 000 now is the inflated cost of the goods Number of future dollars = 15, 000(F/P, 5%, 10) = $24, 434 (d) In order to maintain purchasing power and earn a real return, mo grow by the inflation rate and the interest rate, or if = 13. 4%, as FW = 15, 000(F/P, 13. 4%, 10) = $52, 750 14 -18 © 2012 by Mc. Graw-Hill All Rights Reserved

Capital Recovery with Inflation The A/P and A/F factors require the use of if when inflation is co If a small company invests $150, 000 in a new production line machine, how much must it receive each year to recover the investment in 5 years? The real interest rate is 10% and the inflation rate is Solution: Capital recovery (CR) is the 4% per year. AW value if = 0. 10 + 0. 04 + (0. 10)(0. 04) = 14. 4% CR = AW = 150, 000(A/P, 14. 4%, 5) = $44, 115 per year 14 -19 © 2012 by Mc. Graw-Hill All Rights Reserved

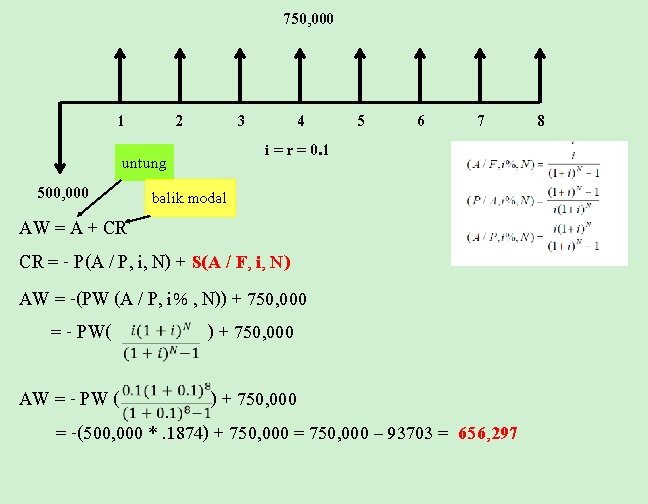
750, 000 1 500, 000 2 untung balik modal 3 4 i = r = 0. 1 5 6 7 AW = A + CR CR = - P(A / P, i, N) + S(A / F, i, N) AW = -(PW (A / P, i% , N)) + 750, 000 = - PW( ) + 750, 000 AW = - PW ( ) + 750, 000 = -(500, 000 *. 1874) + 750, 000 = 750, 000 – 93703 = 656, 297 8

Summary of Important Points Inflation occurs because value of currency has changed Inflation reduces purchasing power; one unit buys less goods ort services Two ways to account for inflation in economic analyses: (1) Convert all cash flows into constant-value dollars and use i During deflation, purchasing powerdollars of money greater in futur (2) Leave cash flows as inflated andisuse if at present Future worth values can have four different interpretations, requiring different interest rates to find FW Use if in calculations involving A/P or A/F when inflation is © 2012 by Mc. Graw-Hill All Rights Reserved 14 -21 considered

Problem 5. 1 An engineer is considering two types of diffusion furnaces, small (S) and large (L), for depositing ultra thin films. A small furnace will cost less to purchase but will have a higher maintenance and therefore, a higher operating cost. In writing the report, the engineer compared the alternatives based on future worth values, but the company president wants the cost expressed as present dollars. Deduce the present worth values if future worth values are FWS = RM 500, 000 and FWL= RM 600, 000. The company uses a real interest rate of 1% per month and an inflation rate of 0. 4% per month. Assume the future worth values were for a 10 -year project period. 1 -22 © 2012 by Mc. Graw-Hill, New York, N. Y All Rights Reserved

Problem 5. 2 Harmony Corporation plans to set aside RM 60, 000 per year beginning 1 year from now for replacing equipment 5 years from now. What will be the purchasing power (in terms of current-value dollars) of the amount accumulated, if the investment grows by 10% per year, but inflation averages 4% per year ? 1 -23 © 2012 by Mc. Graw-Hill, New York, N. Y All Rights Reserved