Effects of Event Ordering on Memory Requirement in

Effects of Event Ordering on Memory Requirement in Parallel Simulation Teo Y. M. , Onggo B. S. S. , and Tay, S. C. Department of Computer Science National University of Singapore MASCOTS 2001

Objectives Propose a methodology to study memory requirement in simulation based on event ordering Apply poset theory (used in discrete maths) to formalize event ordering 12/20/2021 MASCOTS 2001 2

Background Much effort in improving execution time Some work on memory management issues Some focuses on memory analysis using analytical method Lack of formal methodology for studying event ordering 12/20/2021 MASCOTS 2001 3

Outline Modeling & Simulation Process Components of Memory Model Partial Order Set Definition Formalization of Event Orderings Memory Model Experiments Conclusion 12/20/2021 MASCOTS 2001 4

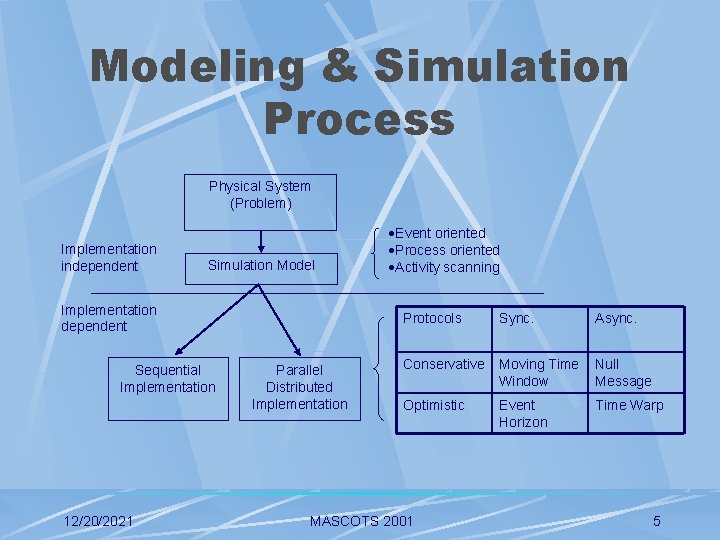
Modeling & Simulation Process Physical System (Problem) Implementation independent Simulation Model Implementation dependent Sequential Implementation 12/20/2021 Parallel Distributed Implementation Event oriented Process oriented Activity scanning Protocols Sync. Async. Conservative Moving Time Window Null Message Optimistic Event Horizon Time Warp MASCOTS 2001 5

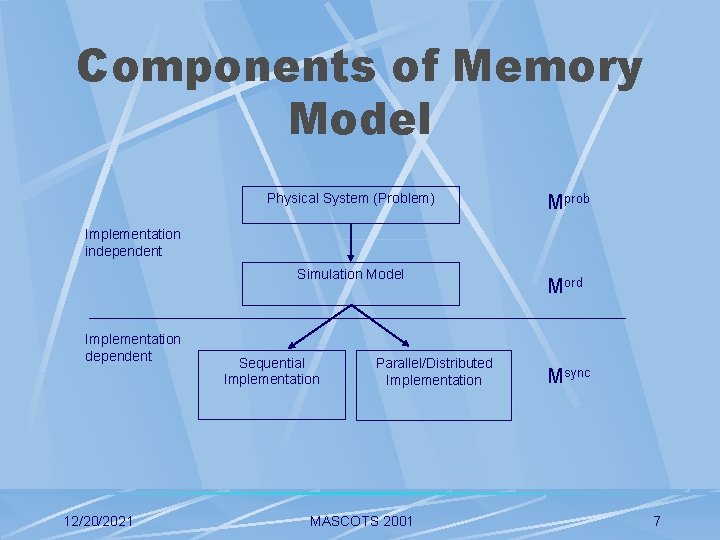
Components of Memory Model Mprob : states of the physical system Mord : future event lists Msync : synchronization overhead (parallel / distributed simulation) 12/20/2021 MASCOTS 2001 6

Components of Memory Model Physical System (Problem) Mprob Implementation independent Simulation Model Implementation dependent 12/20/2021 Sequential Implementation Parallel/Distributed Implementation MASCOTS 2001 Mord Msync 7

Benefits Compares the Mprob between physical systems Understands the effect of event orderings on memory requirement (Mord) before implementation Compares the synchronization costs (Msync) of different protocols 12/20/2021 MASCOTS 2001 8

Partial & Total Order Strong inclusion Reflexive : x S (x, x) R v Transitive: x, y, z S (x, y) R (y, z) R (x, z) R v Weak inclusion Irreflexive: x S (x, x) R v Transitive: as above v Total order: for all x, y S either (x, y) R or (y, x) R 12/20/2021 MASCOTS 2001 9

Partial Order Set Let S be a set, and R is the relation over Sx. S A tuple S, R is a partial order set (poset) if R is partial order on S 12/20/2021 MASCOTS 2001 10

Related Work Lamport (1978): happened-before (partial order) and total order Fujimoto & Weatherly (1996): five message orderings, i. e. , receive order, priority order, causal and totally order, and timestamp order 12/20/2021 MASCOTS 2001 11

Related Work Martini et al. (1997), Rao et. al. (1998): maintain event causality? Preiss (1989), Reiher et. al. (1990), Wieland (1997), Ronngren & Liljenstam (1999): the ordering of simultaneous events in simulation. 12/20/2021 MASCOTS 2001 12

Partial Event Order Let E, par be a poset where E is a set of events E, par is a partial event ordering if: x, y E x comes before y x pary ü x, y E x sends msg to y x pary ü x pary y parz x parz ü ~(x parx) ü 12/20/2021 MASCOTS 2001 13

Timestamp Event Order Assume each e E can be stamped with simulation time, i. e. ts(e) E, ts is a timestamp event ordering if: x, y E ts(x) ts(y) x ts y 12/20/2021 MASCOTS 2001 14

Total Event Order Assume each e E can be stamped with simulation time, i. e. ts(e) E, tot is a total event ordering if: x, y E ts(x) ts(y) x toty ü x, y E ts(x) = ts(y) x has higher priority than y x toty ü 12/20/2021 MASCOTS 2001 15

Proposed Memory Model Total Memory = Mprob + Mord + Msync Partial Event Ordering: Timestamp Event Ordering: Total Event Ordering: 12/20/2021 MASCOTS 2001 16

Time & Space Analyzer (TSA) Simulation code (sequential) Time-Space Analyzer CSIM FEL 12/20/2021 CEL MASCOTS 2001 17

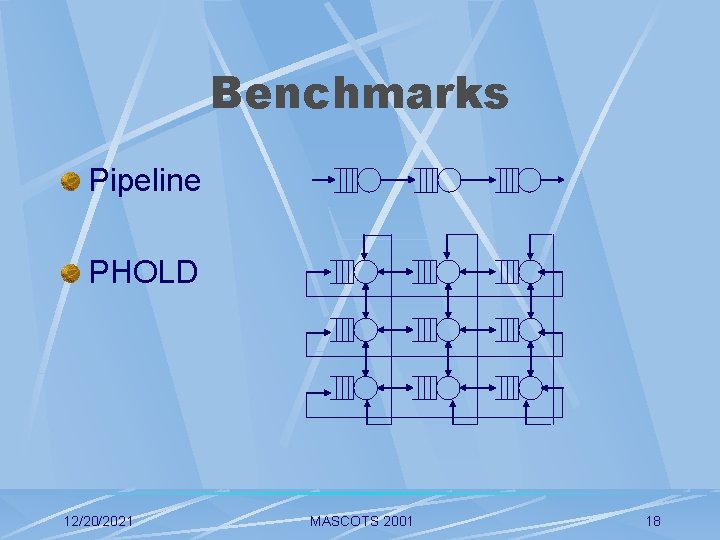
Benchmarks Pipeline PHOLD 12/20/2021 MASCOTS 2001 18

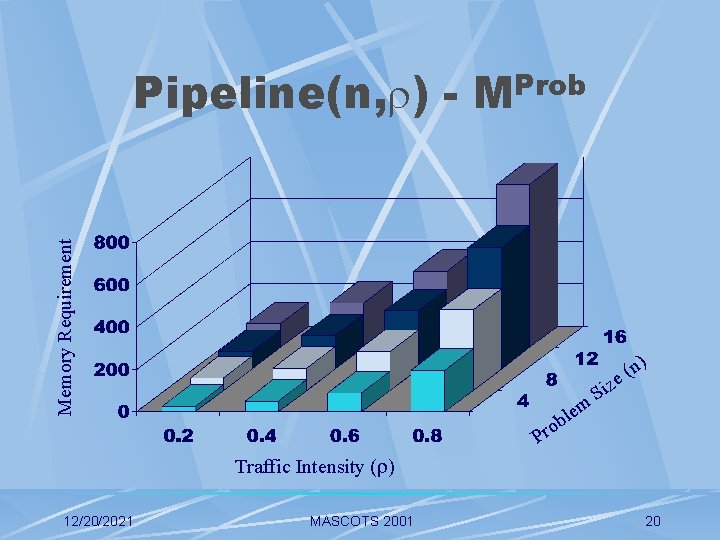
Pipeline (n, ) Parameters: mean interarrival time, mean service time, and number of service centers (n). Homogenous service centers Interarrival time and service time are exponentially distributed, is the traffic intensity. 12/20/2021 MASCOTS 2001 19

Memory Requirement Pipeline(n, ) - MProb n) ( e m le b o Pr Siz Traffic Intensity ( ) 12/20/2021 MASCOTS 2001 20

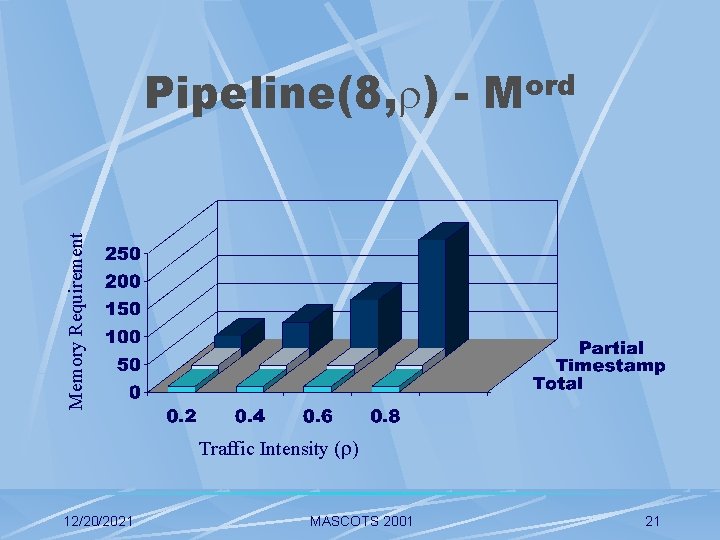
Memory Requirement Pipeline(8, ) - Mord Traffic Intensity ( ) 12/20/2021 MASCOTS 2001 21

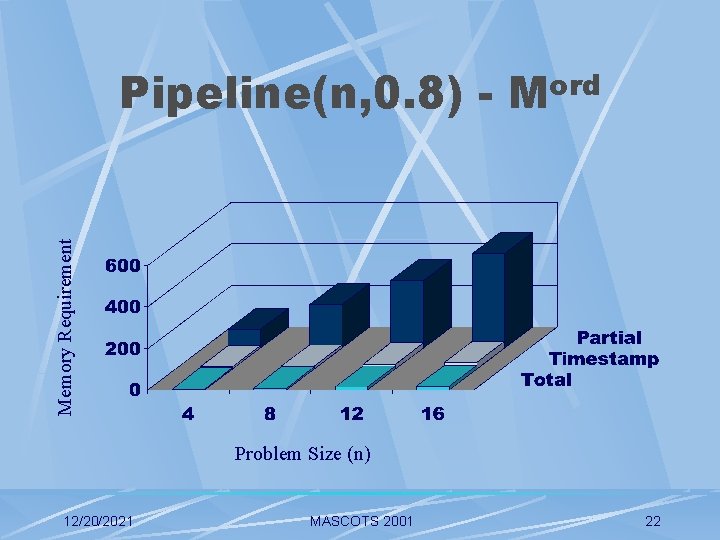
Memory Requirement Pipeline(n, 0. 8) - Mord Problem Size (n) 12/20/2021 MASCOTS 2001 22

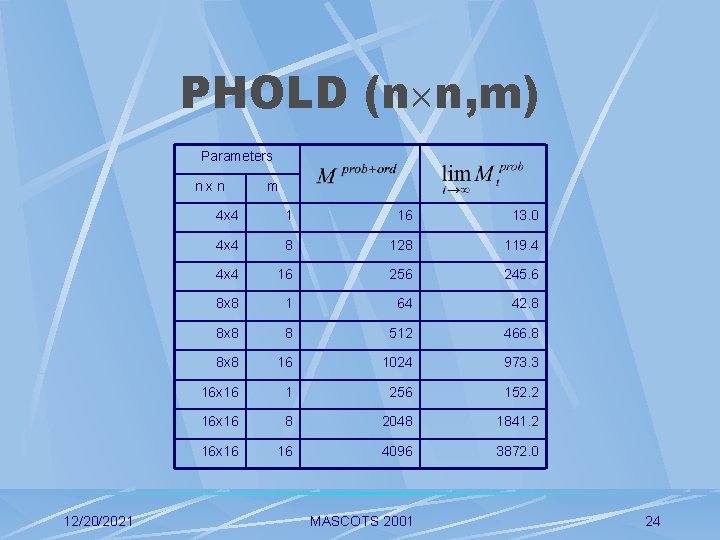
PHOLD (n n, m) Parameters: message density number of service centers (n n) (m), Initial messages are distributed evenly, service time is exponential (1), neighborhood choice is uniformly distributed 12/20/2021 MASCOTS 2001 23

PHOLD (n n, m) Parameters nxn 12/20/2021 m 4 x 4 1 16 13. 0 4 x 4 8 128 119. 4 4 x 4 16 256 245. 6 8 x 8 1 64 42. 8 8 x 8 8 512 466. 8 8 x 8 16 1024 973. 3 16 x 16 1 256 152. 2 16 x 16 8 2048 1841. 2 16 x 16 16 4096 3872. 0 MASCOTS 2001 24

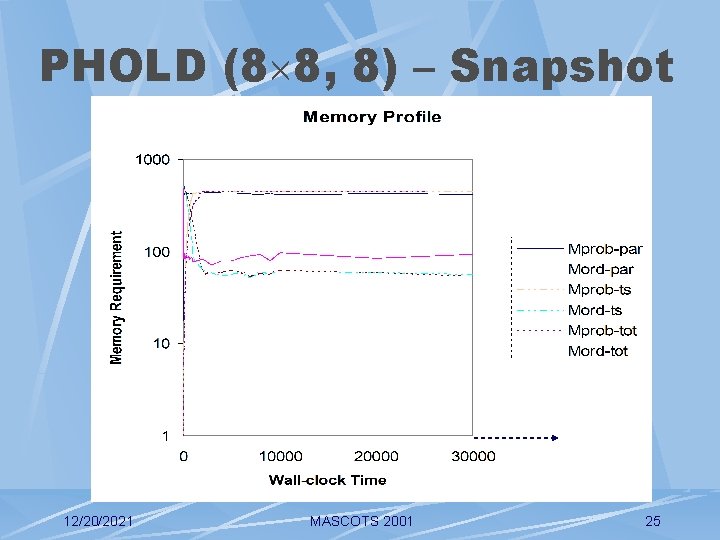
PHOLD (8 8, 8) – Snapshot 12/20/2021 MASCOTS 2001 25

Conclusions The use of poset theory to formalize event orderings A formal approach to analyze memory requirement Mprob depends on the characteristic of the problem Mord depends on the characteristic of the problem and event ordering used 12/20/2021 MASCOTS 2001 26

Conclusions Open system: a weaker event ordered simulation requires more memory than strong ordering Closed system: the total memory required for a given problem size, Mprob + Mord, is constant and independent of event orderings 12/20/2021 MASCOTS 2001 27

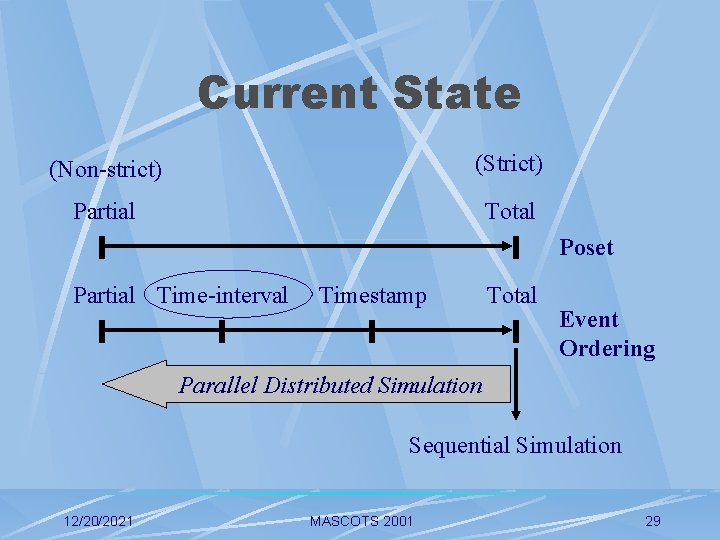
Current State formalized event orderings using poset established relationship amongst event orderings quantified strictness of event orderings implemented four event orderings in TSA – time and space 12/20/2021 MASCOTS 2001 28

Current State (Non-strict) (Strict) Partial Total Poset Partial Time-interval Timestamp Total Event Ordering Parallel Distributed Simulation Sequential Simulation 12/20/2021 MASCOTS 2001 29

References Lamport (1978) Preiss (1989) Reiher et. al. (1990) Fujimoto & Weatherly(1996) Martini et. al. (1997) Wieland (1997) Rao et. al. (1998) Ronngren & Liljenstam (1999) 12/20/2021 MASCOTS 2001 30