Effective Feature Selection Framework for Cluster Analysis of

Effective Feature Selection Framework for Cluster Analysis of Microarray Data Gouchol Pok Keun Ho Ryu Computer Science Dept. Yanbian University China DB/Bioinformatics Lab Chungbuk Nat’l University Korea 1

Outline Background p Motivation p Proposed Method p Experiments p Conclusion p 2

Feature Selection p Definition: n p Process of selecting a subset of relevant features for building robust learning models Objectives: n n Alleviating Enhancing Speeding Improving the effect of the curse of dimensionality generalization capability up learning process model interpretability from Wikipedia: http: //en. wikipedia. org/wiki/Feature_selection 3

Issues in Feature Selection p p p How to compute the degree to which a feature is relevant with the class (discrimination) How to decide if a selected feature is redundant with other features (strongly correlated) How to select features so that classifying power is not diminished (increased) § § § Removal of irrelevancy Removal of redundancy Maintain class-discriminating power 4

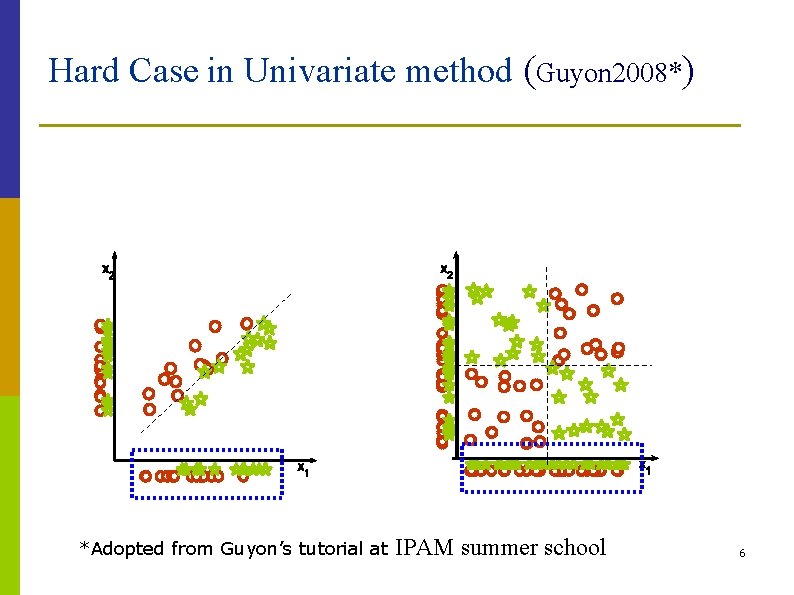
Selection Modes p Univariate method: n n p considers one feature at a time based on score rank measures are Correlation, Information measure, K-S statistic, etc Multivariate method: n n n considers subsets of features altogether Bayesian and PCA based selection in principle, more powerful than univariate method, but not always in practice (Guyon 2008) 5

Hard Case in Univariate method (Guyon 2008*) *Adopted from Guyon’s tutorial at IPAM summer school 6

Proposed method: Motivation p Method that fits 2 -D microarray data n p typical forms: thousands of genes (rows) and hundreds of samples (columns) Multivariate approach n Feature relevancy and redundancy are addressed simultaneously 7

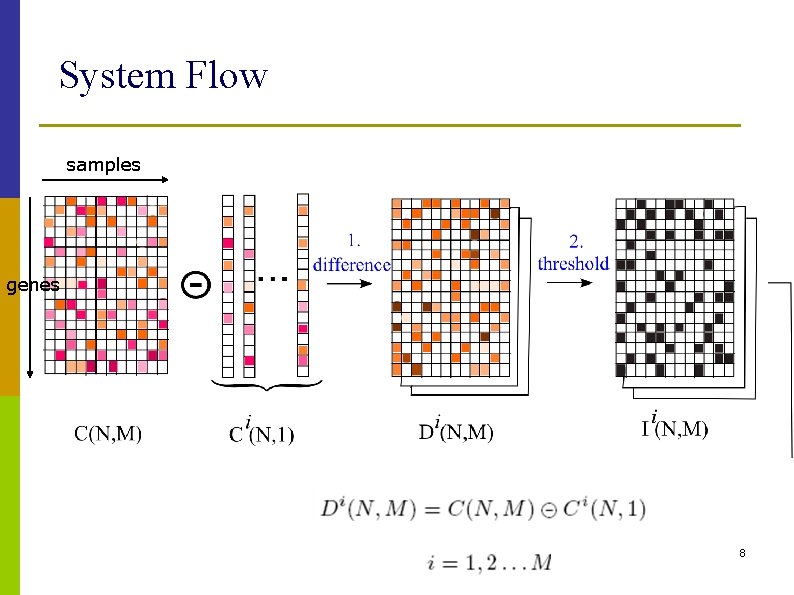
System Flow samples genes 8

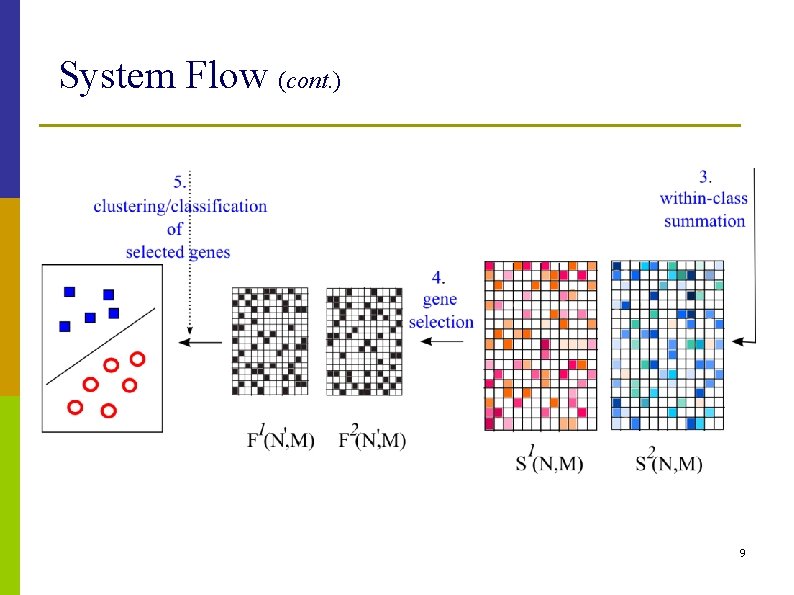
System Flow (cont. ) 9

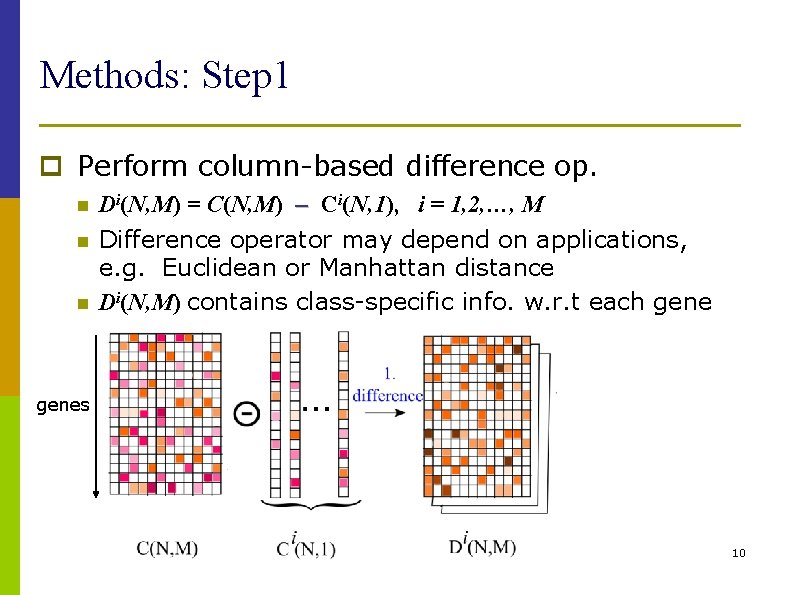
Methods: Step 1 p Perform column-based difference op. n n n Di(N, M) = C(N, M) Ci(N, 1), i = 1, 2, …, M Difference operator may depend on applications, e. g. Euclidean or Manhattan distance Di(N, M) contains class-specific info. w. r. t each genes 10

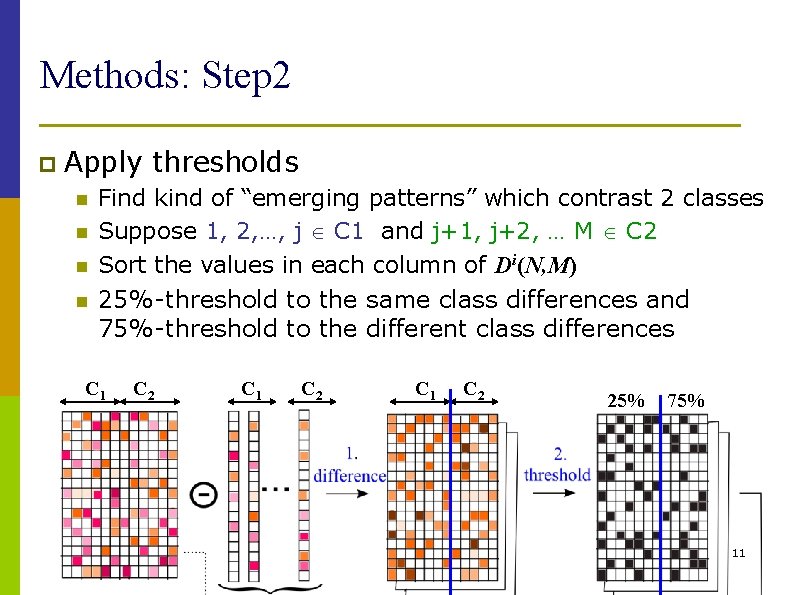
Methods: Step 2 p Apply n n thresholds Find kind of “emerging patterns” which contrast 2 classes Suppose 1, 2, …, j C 1 and j+1, j+2, … M C 2 Sort the values in each column of Di(N, M) 25%-threshold to the same class differences and 75%-threshold to the different class differences C 1 C 2 25% 75% 11

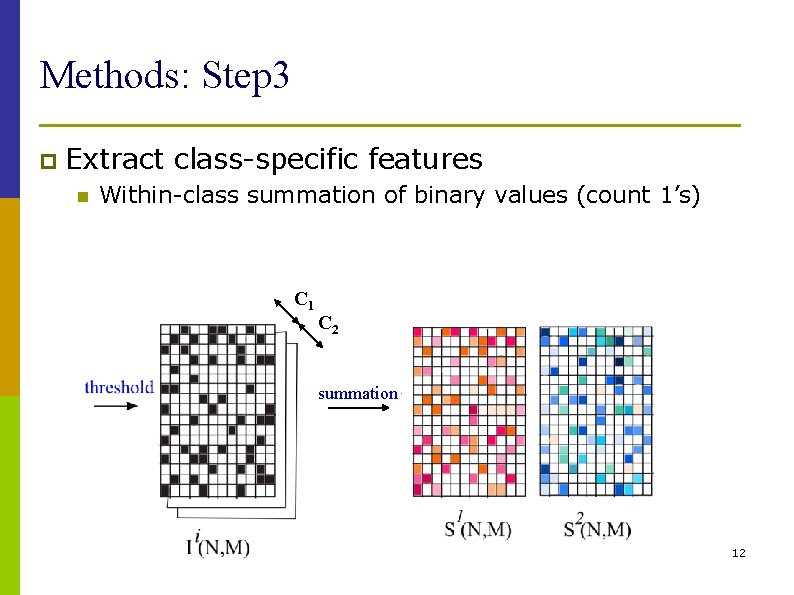
Methods: Step 3 p Extract n class-specific features Within-class summation of binary values (count 1’s) C 1 C 2 summation 12

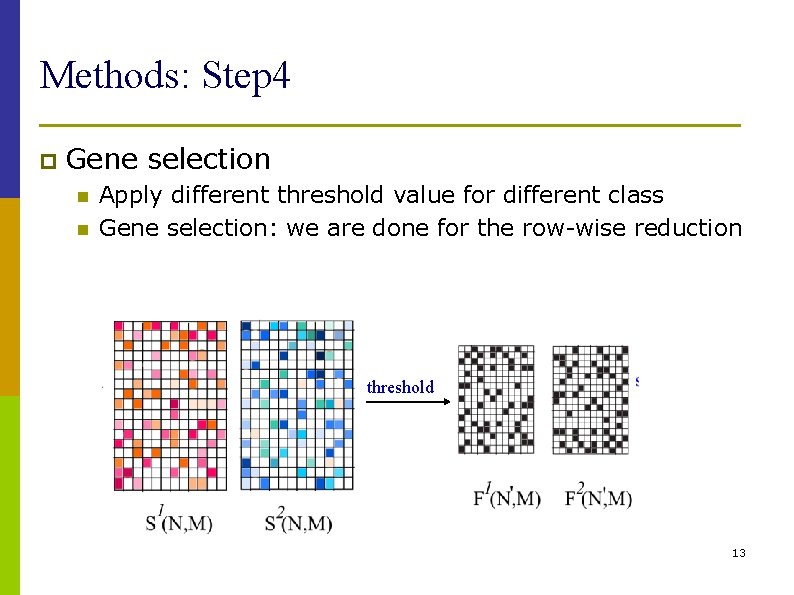
Methods: Step 4 p Gene n n selection Apply different threshold value for different class Gene selection: we are done for the row-wise reduction threshold 13

Methods: Step 5 p Column-wise n n reduction by clustering Classification of samples Applied NMF method 14

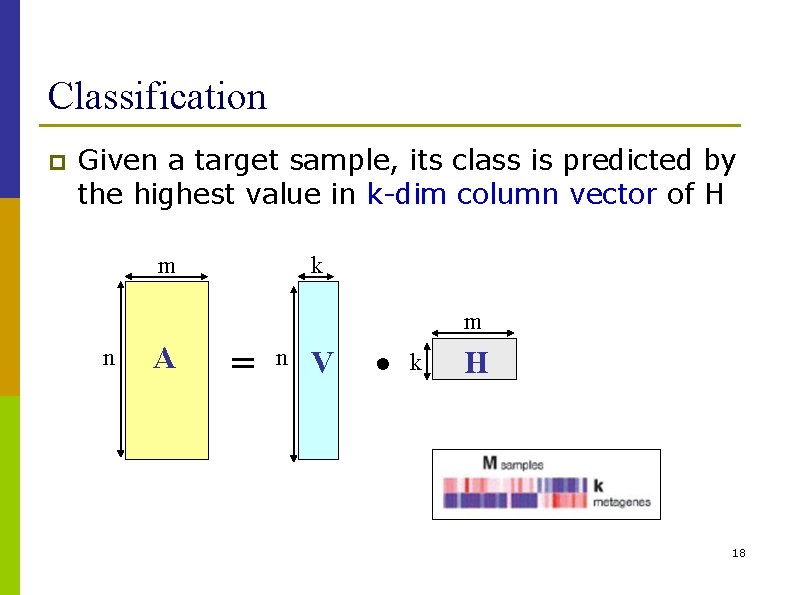
Nonnegative Matrix Factorization (NMF) p Matrix factorization: A ~ VH A: n m matrix of n genes and m samples. V: (n k): k columns of V are called basis vectors H: (k m): describes how strongly each building block is present in measurement vectors m k m n A = n V • k H 15

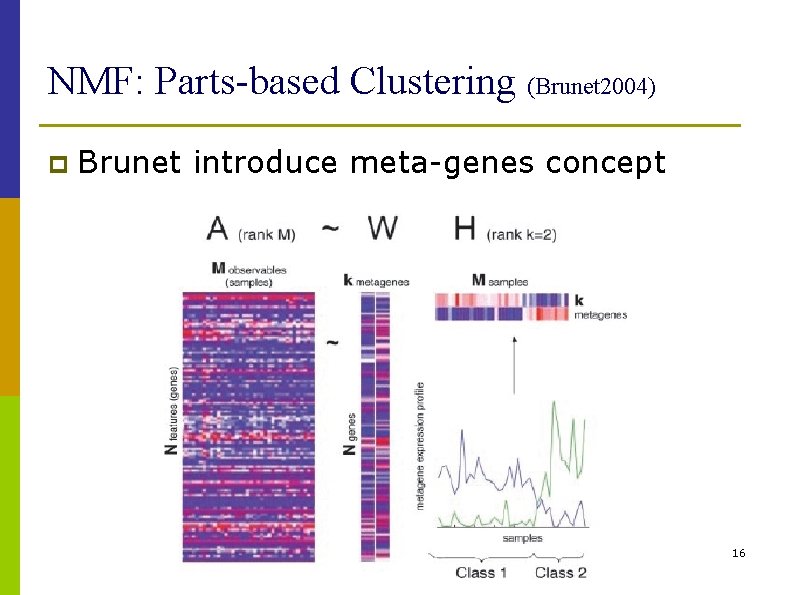
NMF: Parts-based Clustering (Brunet 2004) p Brunet introduce meta-genes concept 16

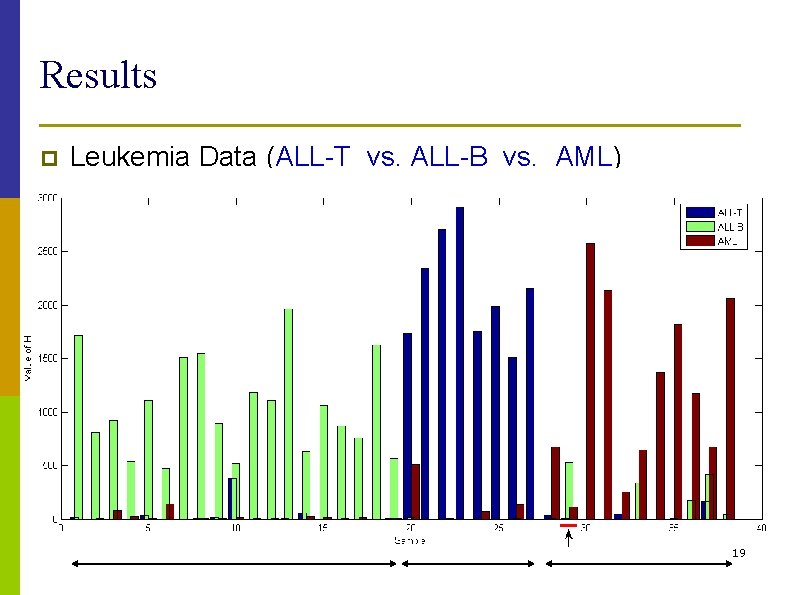
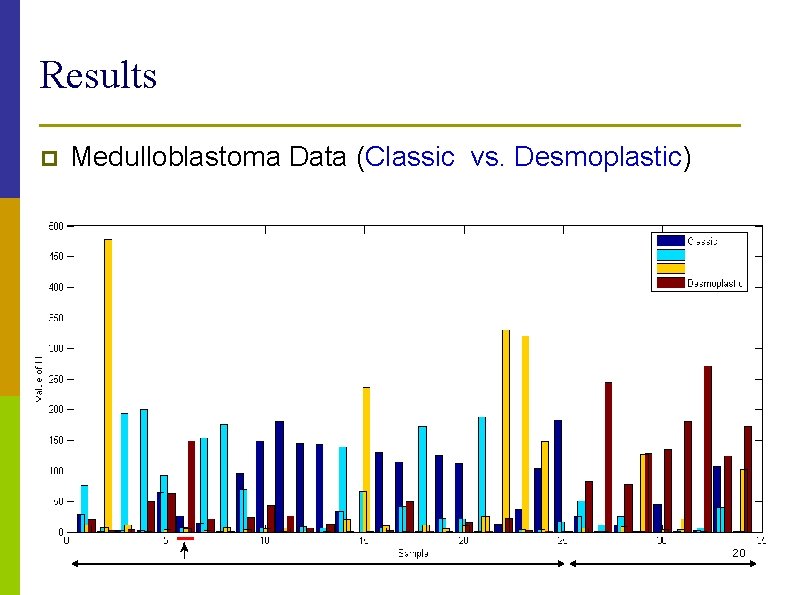
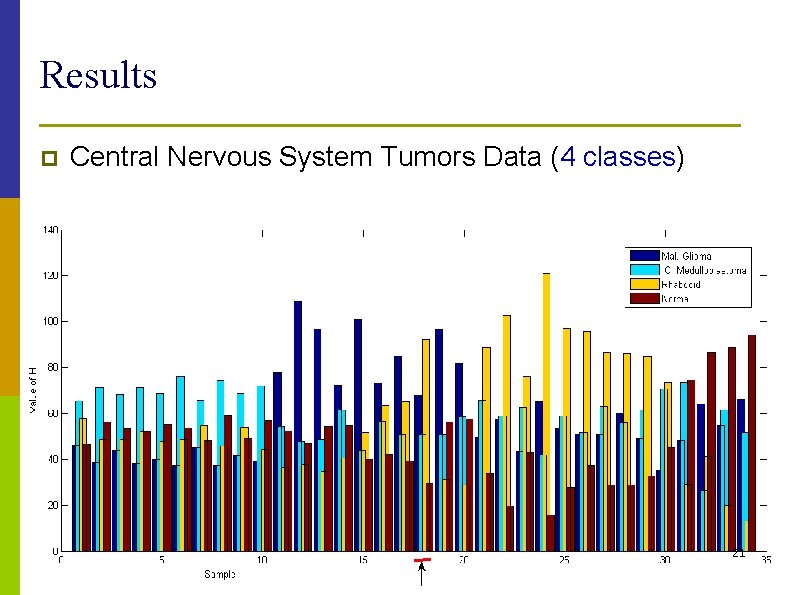
Experiments: Datasets p Leukemia Data n n 5000 genes 38 samples of two classes p p p Medulloblastoma Data n n 5893 genes 34 samples of two classes p p 19 samples of ALL-B and 8 samples of ALL-T type, 11 samples of AML type. 25 classic type and 9 desmoplastic medulloblastoma type Central Nervous System Tumors Data n n 7129 samples 34 samples of four classes p 10 classic medulloblastomas, 10 malig-nant gliomas, 10 rhabdoids, and 17 4 normals

Classification p Given a target sample, its class is predicted by the highest value in k-dim column vector of H m k m n A = n V • k H 18

Results p Leukemia Data (ALL-T vs. ALL-B vs. AML) 19

Results p Medulloblastoma Data (Classic vs. Desmoplastic) 20

Results p Central Nervous System Tumors Data (4 classes) 21

Conclusions & Future work p Our approach tries to capture a group of features, but in contrast to holistic methods such as PCA and ICA, intrinsic structure of data distribution is preserved in the reduced space. p Still, PCA and ICA can be used as an aide to look into the data distribution structure, and provide useful information for further processing to other methods. n Our on-going research is on how to combine the PCA and ICA to the proposed work 22

References p p p Wikipedia, http: //en. wikipedia. org/wiki/Feature_selection J. -P. Brunet, P. Tamayo, T. Golub, and J. P. Mesirov. Metagenes and molecular pattern discovery using matrix factorization. PNAS, 101(12): 4164 -4169, 2004. L. Yu and H. Liu. Feature selection for high-dimensional data: A fast correlation-based filter solution. In Proc 12 th Int Conf on Machine Learning (ICML-03), pages 856– 863, 2003 Biesiada J, Duch W (2005), Feature Selection for High-Dimensional Data: A Kolmogorov-Smirnov Correlation-Based Filter Solution. (CORES'05) Advances in Soft Computing, Springer Verlag, pp. 95104, 2005. D. D. Lee and H. S. Seung, Learning the parts of objects by nonnegative matrix factorization 23

Questions? 24