Effective Action of Wall Loops Takayuki Nagashima In

Effective Action of Wall Loops Takayuki Nagashima In collaboration with M. Eto, T. Fujimori, M. Nitta, K. Ohashi and N. Sakai

Domain Wall Junctions l l l Domain wall junctions were first discussed in 1999 by Gibbons and Townsend. They were found to be ¼ BPS states preserving only a quarter of supersymmetry. Since then many works about BPS or nearly BPS domain wall webs have been done. However most works relied on qualitative treatments or numerical simulations. Recently exact solutions of domain wall webs have been found in a supersymmetric gauge theory (Eto. et. al. 2005). Examples of domain wall webs

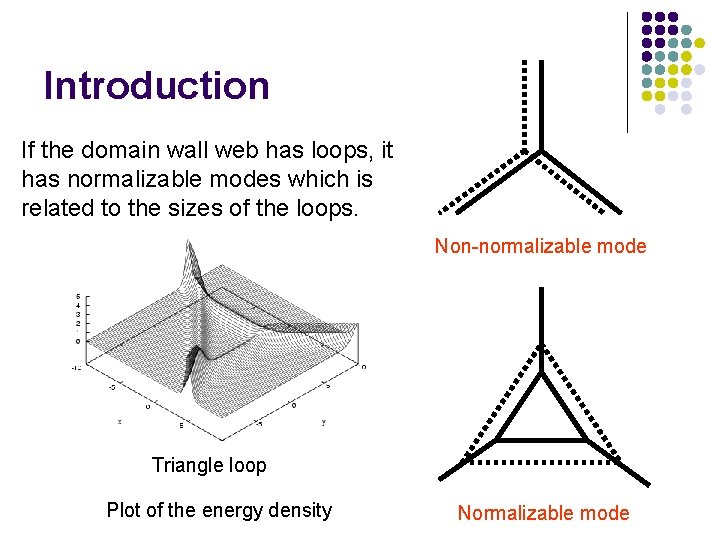
Introduction If the domain wall web has loops, it has normalizable modes which is related to the sizes of the loops. Non-normalizable mode Triangle loop Plot of the energy density Normalizable mode

Model and It’s Vacua Model : d=3+1 8 SUSY U(Nc) gauge theory with Nf fundamental hypermultiplets. Vacua

BPS Equations for Webs of Walls All the moduli parameters V-equivalence relation

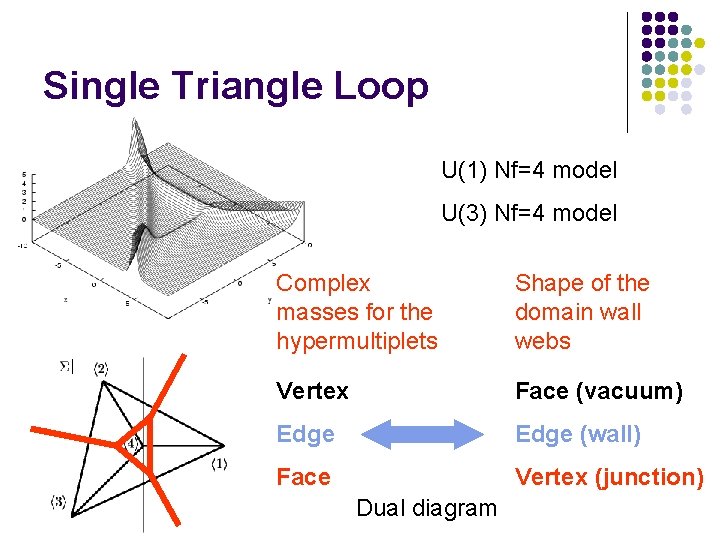
Single Triangle Loop U(1) Nf=4 model U(3) Nf=4 model Complex masses for the hypermultiplets Shape of the domain wall webs Vertex Face (vacuum) Edge (wall) Face Vertex (junction) Dual diagram

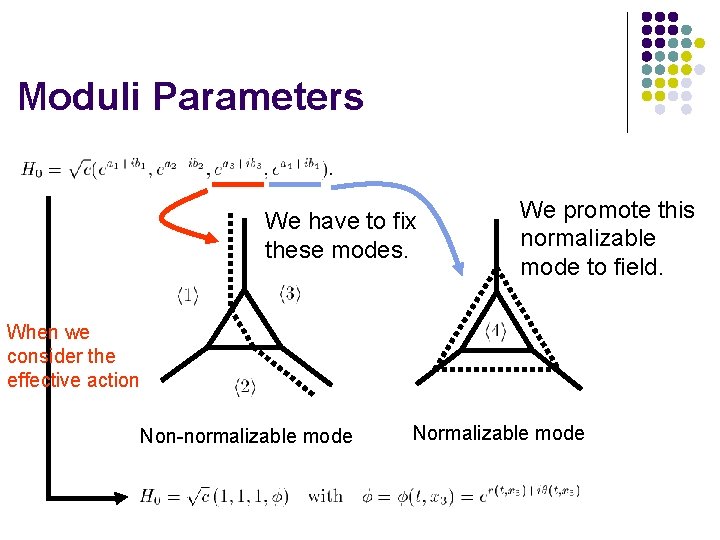
Moduli Parameters We have to fix these modes. We promote this normalizable mode to field. When we consider the effective action Non-normalizable mode Normalizable mode

Effective Action of Webs of Walls It is well known that the effective action of BPS solitons is obtained from the kinetic term of the original Lagrangian. Although the master equation is difficult to solve, we can proceed some calculations to obtain the general formula of the effective action without using the solution of the master equation. Substitute the explicit solution of the master equation into this formula and perform the integral.

Explicit Solution Strong coupling limit Neglect the second term Remove the moduli-independent divergence

Kahler Potential in the Case of Small Loop As long as Minimum of Scalar curvature This is finite. Next let us investigate the metric for large , asymptotic metric. The moduli space is non-singular at

In order to Know the Asymptotic Metric Although the series have convergence region, we can rewrite it as a sum of hypergeometric functions. Therefore we can know the behaviour of the function outside the convergence region using the analytic continuation. However we have not found the expansion of the hypergeometric functions at large in any literature. Here we propose the another simple approach to know the asymptotic (large loop) metric which we call “tropical limit”.

Asymptotic Metric (Large Loop) Tropical limit Pick up only the largest term in each region Remove the moduli-independent divergence Corrections does not contain.

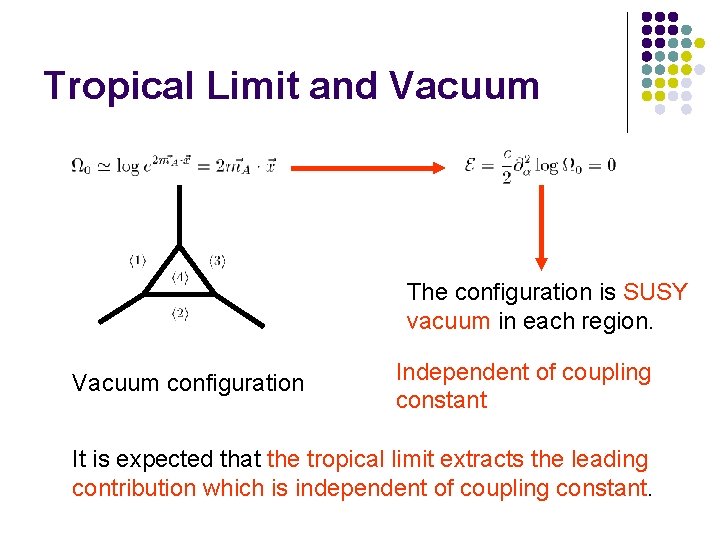
Tropical Limit and Vacuum The configuration is SUSY vacuum in each region. Vacuum configuration Independent of coupling constant It is expected that the tropical limit extracts the leading contribution which is independent of coupling constant.

Another Contribution We use this vacuum expectation value in each region to evaluate the second term without using explicit solutions.

Sum of Two Contributions U(1) gauge theory The same configuration also appears in U(3) gauge theory The only difference is the sign of the second term.

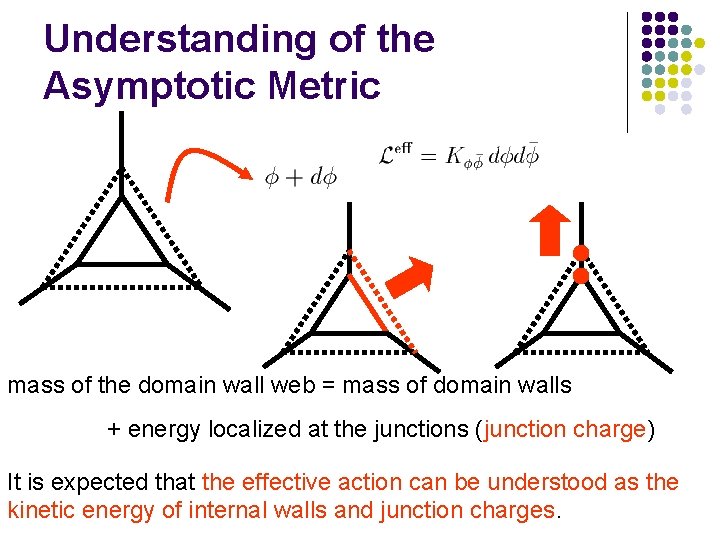
Understanding of the Asymptotic Metric mass of the domain wall web = mass of domain walls + energy localized at the junctions (junction charge) It is expected that the effective action can be understood as the kinetic energy of internal walls and junction charges.

Kinetic Energy of Internal Walls Kinetic energy of internal walls We have to explain two kinds of junction charges.

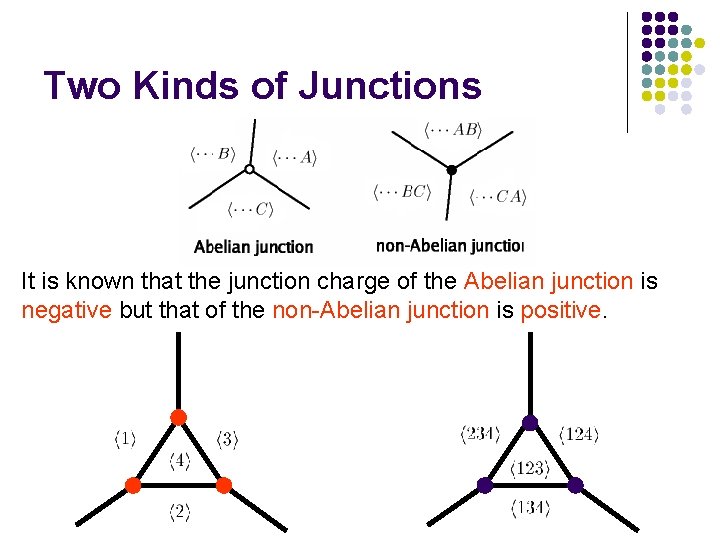
Two Kinds of Junctions It is known that the junction charge of the Abelian junction is negative but that of the non-Abelian junction is positive.

Kinetic Energy of Junction Charges U(1) Gauge Theory U(3) Gauge Theory

Shape of the Moduli Space Finally, let us raise the shape of the moduli space. The metric is obtained by numerical calculation and we embed it into the Euclidean 3 -dimensional space. Non-singular at the tip of the manifold with positive curvature Geometry beween a cone and a cigar.

Summary l l l We have succeeded to construct the effective action of wall loops. The Kahler potential can be written as a finite sum of hypergeometric functions. The asymptotic metric can be obtained by the simple method which we call tropical limit. The asymptotic metric can be interpreted as the kinetic energy of internal walls and junction charges. This interpretation explains the sign flip of the asymptotic metric.