Effect of Final state interaction and Coulomb distortion

Effect of Final state interaction and Coulomb distortion of charged current neutrino-nucleus scattering in quasi-elastic region K. S. Kim School of Liberal Arts and Science, Korea Aerospace University, Korea 1. Introduction 2. Formalism 3. Results 4. Summary and conclusion

Introduction Motivation : • Is there loss of flux in the inclusive neutrino scattering ? ( no detection of the knocked-out nucleon ) • Is Coulomb effect of charged current neutrino-nucleus scattering different from electron scattering ? Goal : Investigate the contribution of the final state interaction (FSI) on the total cross section. • Study Coulomb effect in charged current neutrino-nucleus scattering. l

Ingredients : • Calculate total cross section for the neutral and charged current reactions in quasi-elastic region for 12 C nucleus. • Use a relativistic single particle model ( s – w model ). • Compare a relativistic optical potential generated by OSU group and a same potential of the bound nucleon for the FSI of knocked out nucleons. • Compare our results with experimental data by scaling the number of nucleons. • Include the Coulomb distortion of final leptons for charged current reaction using approximate method developed by Ohio University group.

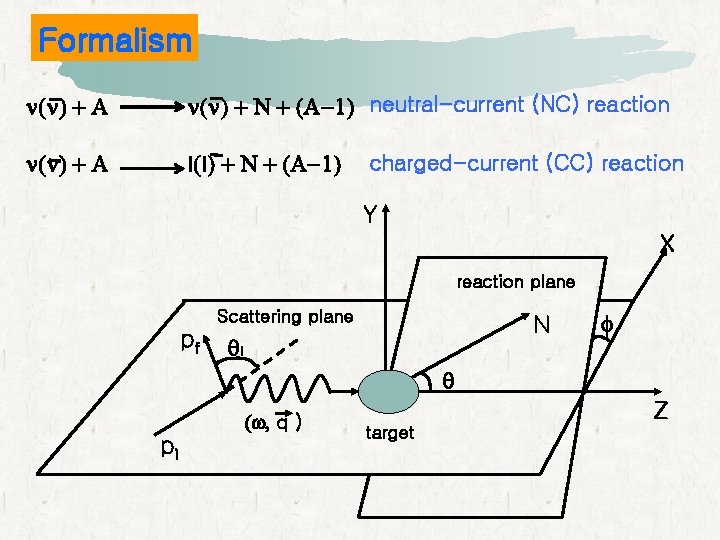
Formalism n(n) + A n(n) + N + (A-1) neutral-current (NC) reaction n(n) + A l(l) + N + (A-1) charged-current (CC) reaction Y X reaction plane Scattering plane pf N ql f q pi (w, q ) Z target

The relativistic nucleon weak current operator weak vector form factors : strange magnetic moment : Weinberg angle

The axial form factors are given by for NC for CC : axial cut-off mass : pseudoscalar form factor disappears for NC reaction : pion mass

Neutrino-nucleus (12 C) scattering The differential cross section is given by : mass of nucleon : mass of residual nucleus : mass of target nucleus : helicity for neutrino (antineutrino) The recoil factor is given by

The kinematic factor is defined by NC reaction CC reaction : mass of Z- and W-boson and : scattering angle : Cabibbo angle Nucleon current represents the Fourier transform given by For the NC reaction, the kinematic factors are given by The response functions are given by

For the CC reaction, the kinematics factors are given by and corresponding response functions are given by with The total cross section

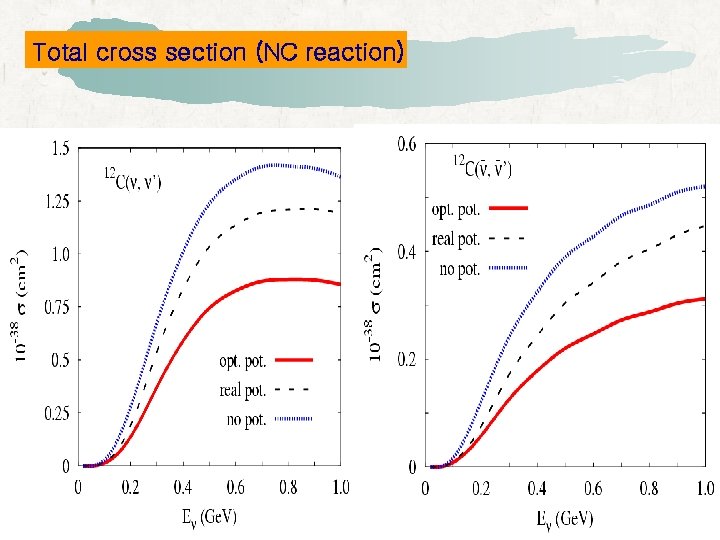
Total cross section (NC reaction)

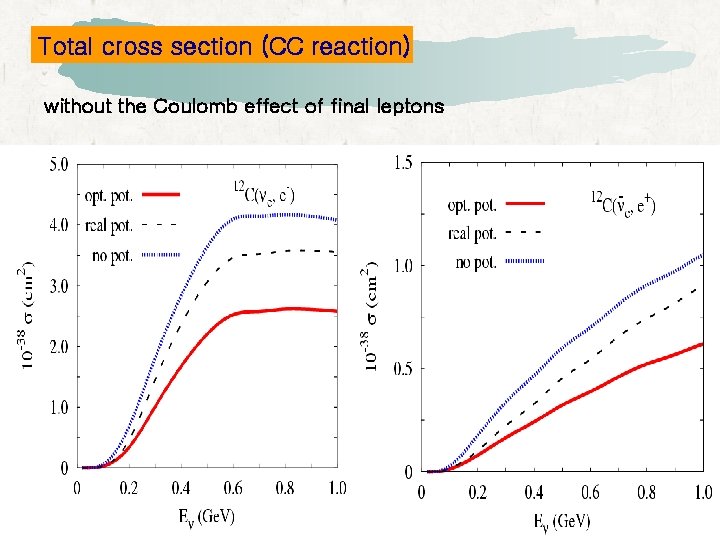
Total cross section (CC reaction) without the Coulomb effect of final leptons

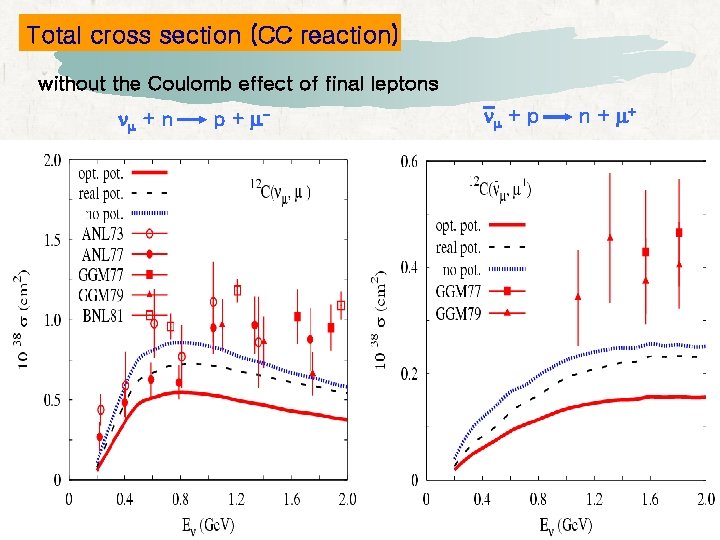
Total cross section (CC reaction) without the Coulomb effect of final leptons nm + n p + m- nm + p n + m+

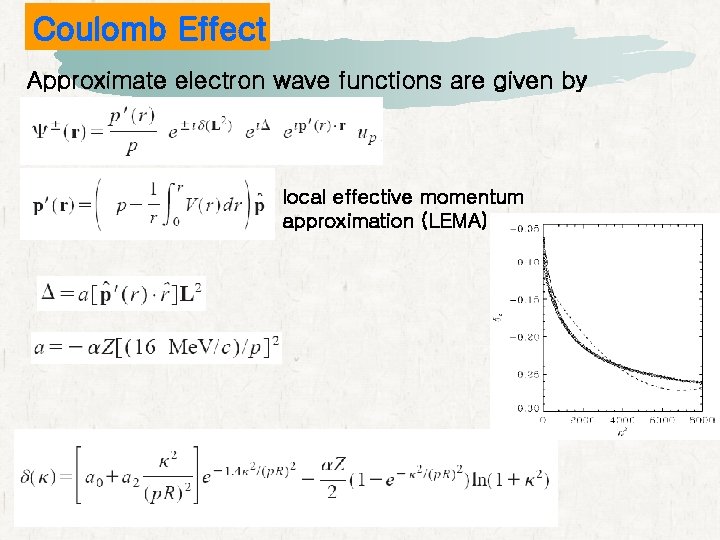
Coulomb Effect Approximate electron wave functions are given by local effective momentum approximation (LEMA)

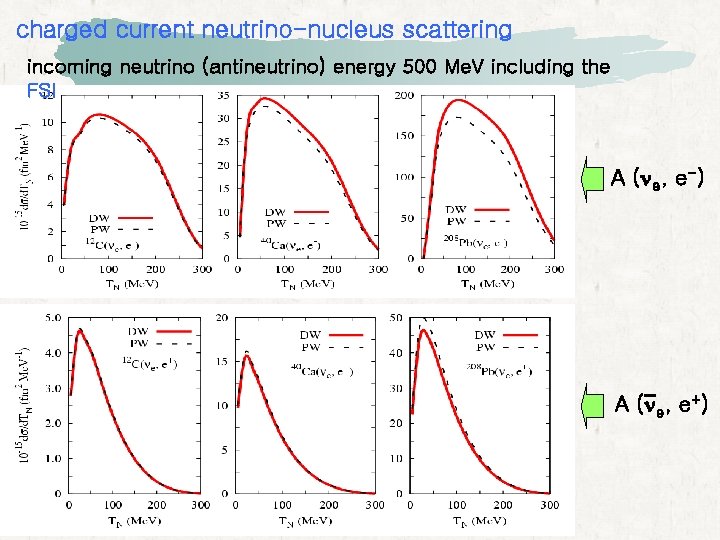
charged current neutrino-nucleus scattering incoming neutrino (antineutrino) energy 500 Me. V including the FSI A (ne, e-) A (ne, e+)

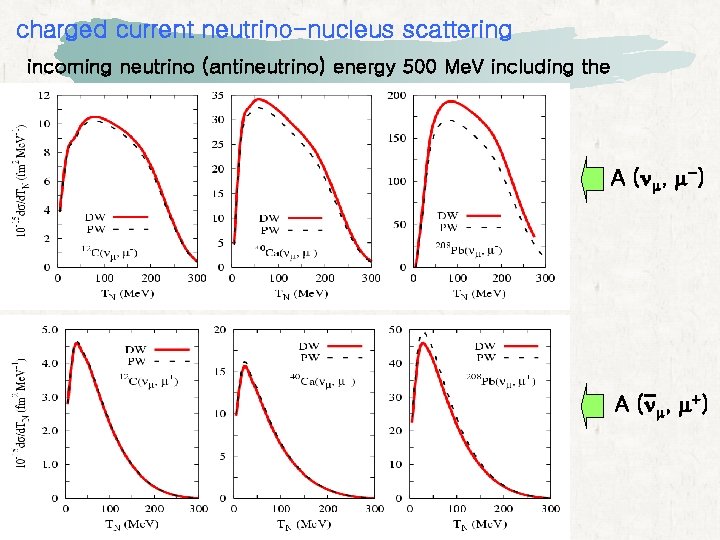
charged current neutrino-nucleus scattering incoming neutrino (antineutrino) energy 500 Me. V including the FSI A (nm, m-) A (nm, m+)

Summary l The effect of the FSI on the NC total cross section is about 50% for the optical potential and about 15% for the real potential for both incident neutrino and antineutrino. • For the CC reaction, the effect reduces the total cross section about 50% for the optical potential and about 15% for the real potential for the incident neutrino and antineutrino without the Coulomb distortion of the final leptons. • At low energies, the real potential describes the experimental data better than the optical potential for the neutrino-muon reaction. • In (e, e’) reaction, the electron Coulomb distortion effect is of the order of 3 % for 12 C, 7 % for electron energy. 40 Ca, and 30 % for 208 Pb at intermediate

• In (ne, e-) reaction and (nm, m-), the Coulomb distortion effect is about 2 % for 12 C, 4 % for energy 500 Me. V. 40 Ca, and 13 % for 208 Pb at incident neutrino • In (ne, e+) reaction and (nm, m+), the Coulomb distortion effect is about 1 % for 12 C, 3 % for energy 500 Me. V. 40 Ca, and 8 % for 208 Pb at incident antineutrino • As for the case of positron, the Coulomb effect of (ne, e+) and (nm, m+) reactions tends to saturate. • The effect of the Coulomb distortion is about half of the electron scattering. • In conclusion, it is difficult to say whethere is loss of flux, or not because of no enough experimental data even with inclusion of the Coulomb effect.