EET 1073 DIGITAL ELECTRONICS 1 Chapter 3 Sequential

EET 107/3 DIGITAL ELECTRONICS 1 Chapter 3: Sequential Logic Design (Part 2. 1)

3. 2 COUNTER INTRODUCTION A counter – a group of flip-flops connected together to perform counting operations. The number of flip-flops used and the way in which they are connected determine the number of states (modulus). Two broad categories according to the way they are clocked: Asynchronous counter Synchronous counter

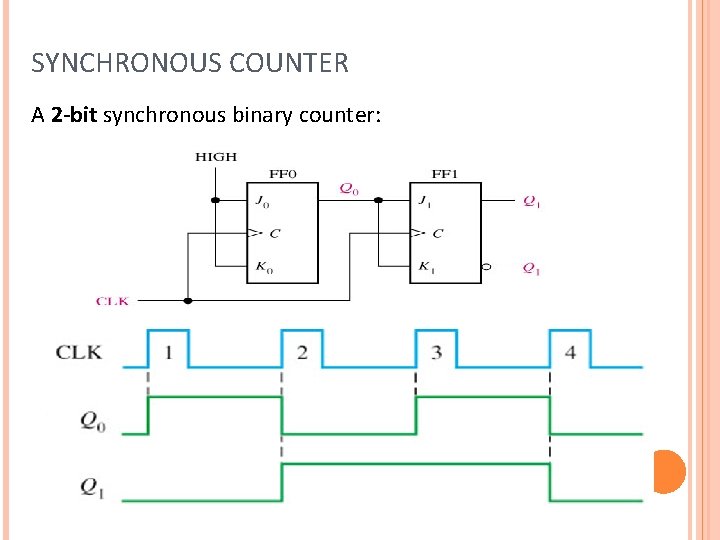
SYNCHRONOUS COUNTER A 2 -bit synchronous binary counter:

SYNCHRONOUS COUNTER Timing details for the 2 -bit synchronous counter operation (the propagation delays of both flip-flops are assumed to be equal):

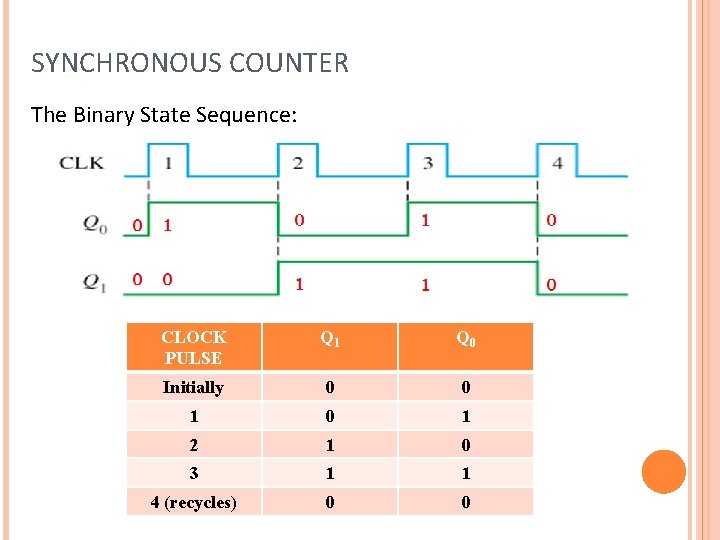
SYNCHRONOUS COUNTER The Binary State Sequence: CLOCK PULSE Q 1 Q 0 Initially 0 0 1 2 1 0 3 1 1 4 (recycles) 0 0

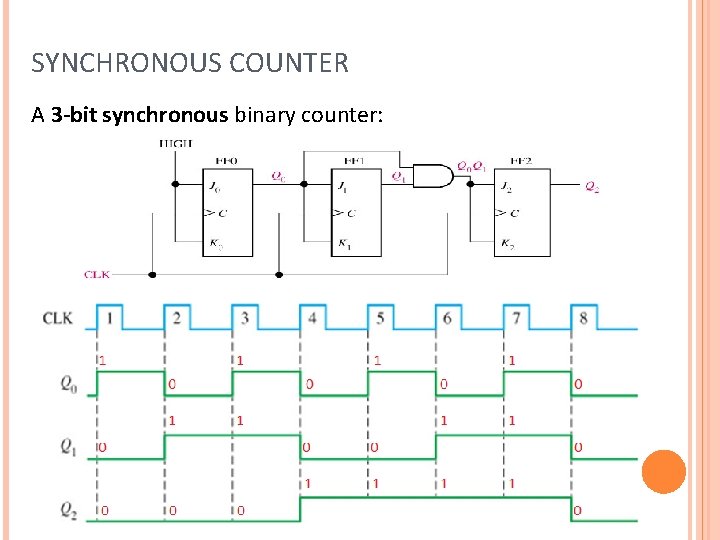
SYNCHRONOUS COUNTER A 3 -bit synchronous binary counter:

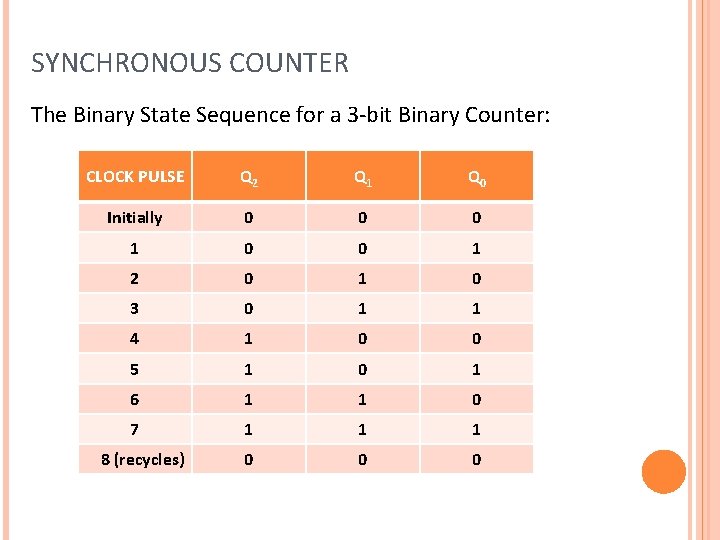
SYNCHRONOUS COUNTER The Binary State Sequence for a 3 -bit Binary Counter: CLOCK PULSE Q 2 Q 1 Q 0 Initially 0 0 0 1 2 0 1 0 3 0 1 1 4 1 0 0 5 1 0 1 6 1 1 0 7 1 1 1 0 0 0 8 (recycles)

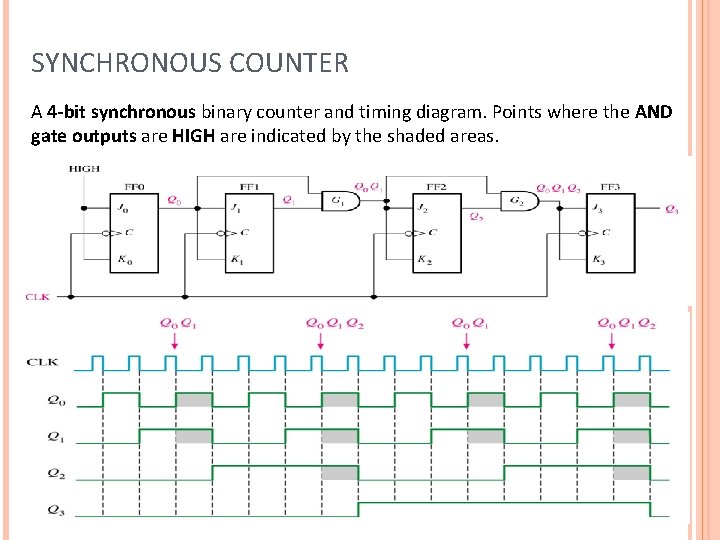
SYNCHRONOUS COUNTER A 4 -bit synchronous binary counter and timing diagram. Points where the AND gate outputs are HIGH are indicated by the shaded areas.

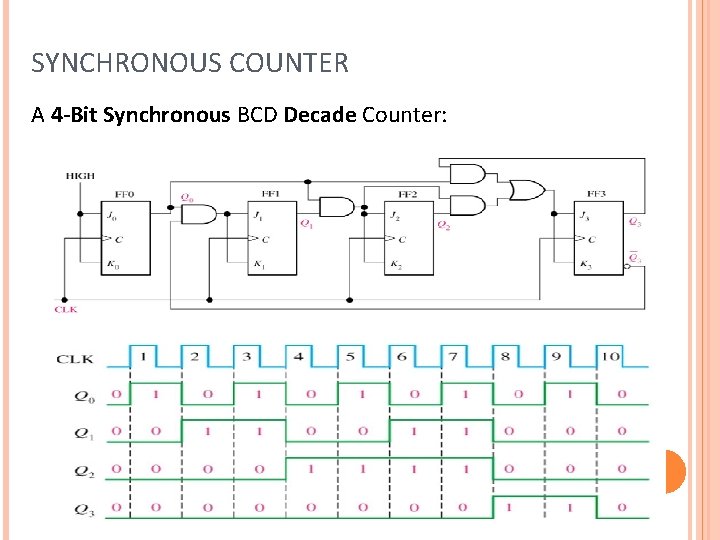
SYNCHRONOUS COUNTER A 4 -Bit Synchronous BCD Decade Counter:

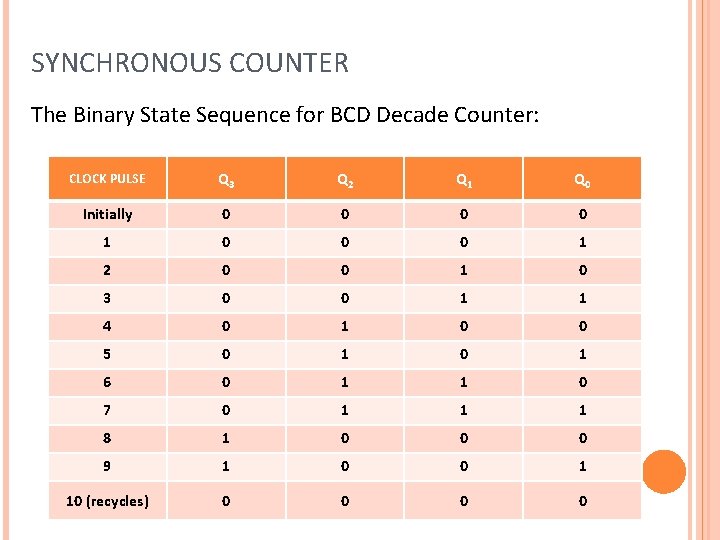
SYNCHRONOUS COUNTER The Binary State Sequence for BCD Decade Counter: CLOCK PULSE Q 3 Q 2 Q 1 Q 0 Initially 0 0 1 0 0 0 1 2 0 0 1 0 3 0 0 1 1 4 0 1 0 0 5 0 1 6 0 1 1 0 7 0 1 1 1 8 1 0 0 0 9 1 0 0 1 10 (recycles) 0 0

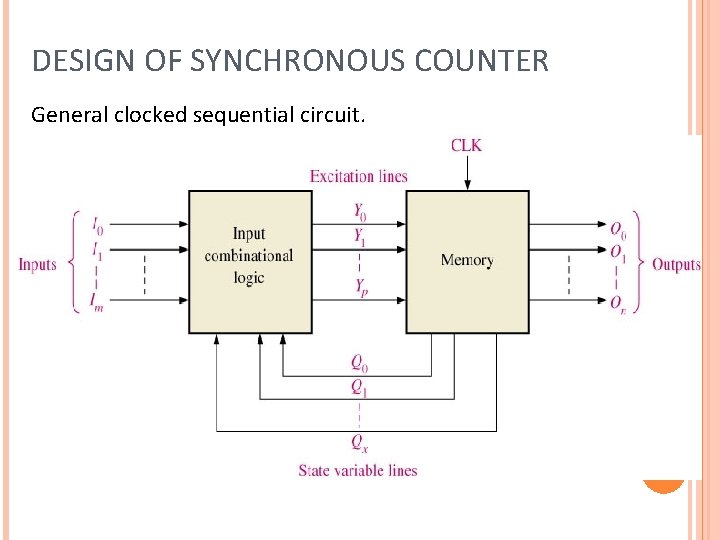
DESIGN OF SYNCHRONOUS COUNTER General clocked sequential circuit.

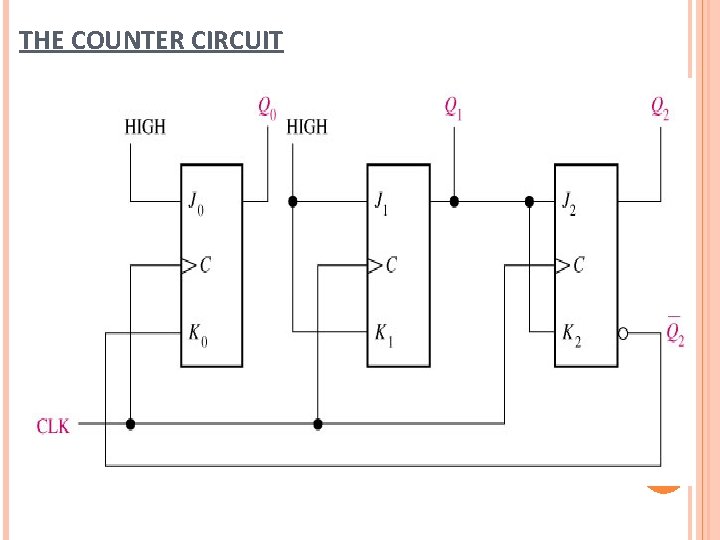
DESIGN OF SYNCHRONOUS COUNTER Steps used in the design of sequential circuit: 1. Specify the counter sequence and draw a state diagram 2. Derive a next-state table from the state diagram 3. Develop a transition table showing the flip-flop inputs required for each transition. The transition table is always the same for a given type of flip-flop 4. Transfer the J and K states from the transition table to Kmaps. There is a K-map for each input of each flip-flop. 5. Group the K-map cells to generate and derive the logic expression for each flip-flop input. 6. Implement the expressions with combinational logic, and combine with the flip-flops to create the counter.

DESIGN OF SYNCHRONOUS COUNTER Example: 1. Design a Modulus-4 synchronous up-counter. Use D flip-flops. 2. Design a Modulus-4 synchronous up-counter. Use T flip-flops. 3. Design a Modulus-4 synchronous up-counter. Use JK flip-flops. 4. Design a Modulus-4 synchronous up-counter. Use SR flip-flops.

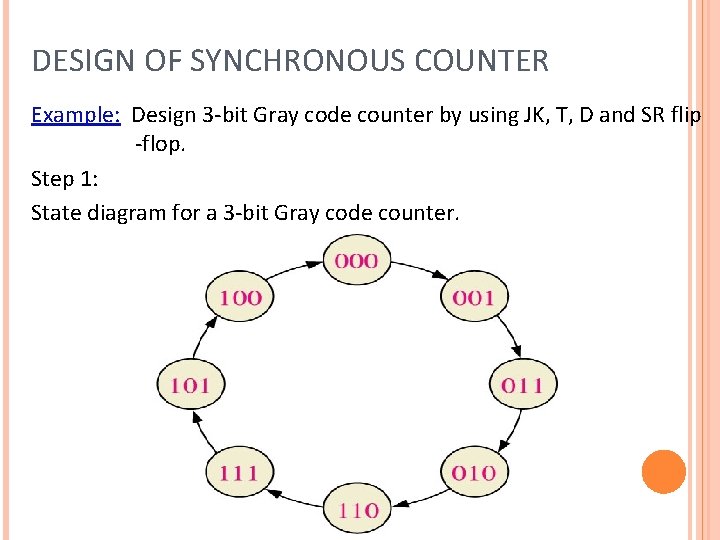
DESIGN OF SYNCHRONOUS COUNTER Example: Design 3 -bit Gray code counter by using JK, T, D and SR flip -flop. Step 1: State diagram for a 3 -bit Gray code counter.

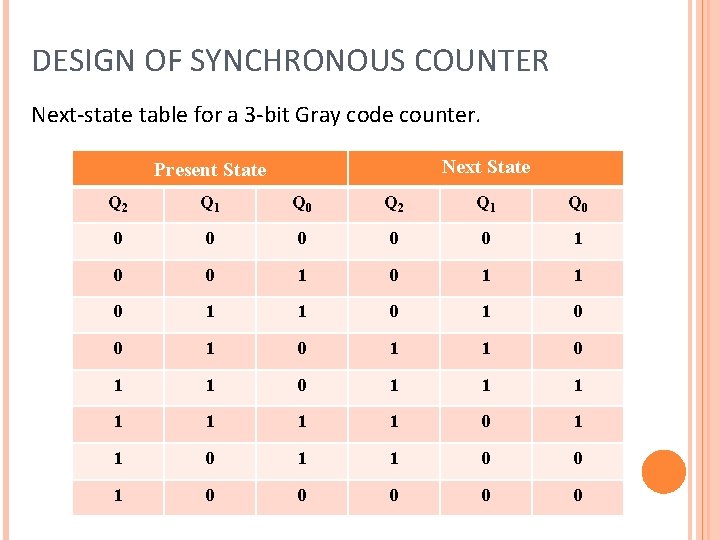
DESIGN OF SYNCHRONOUS COUNTER Next-state table for a 3 -bit Gray code counter. Next State Present State Q 2 Q 1 Q 0 0 0 0 1 0 1 1 0 1 1 1 1 0 0 0 0 0

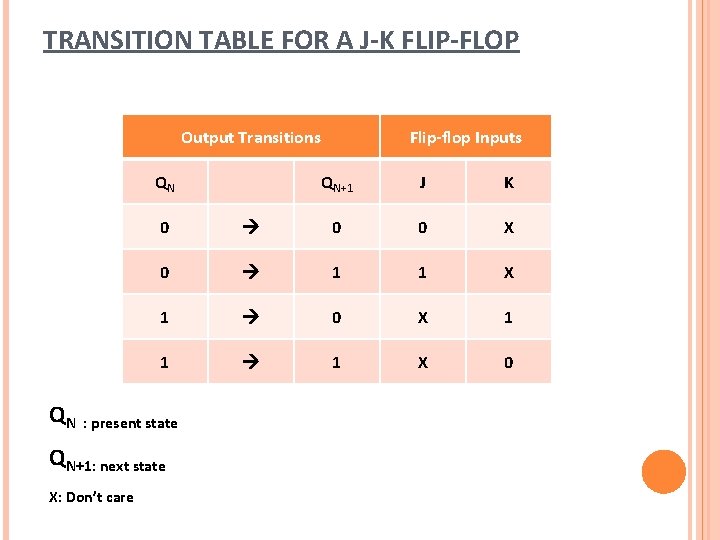
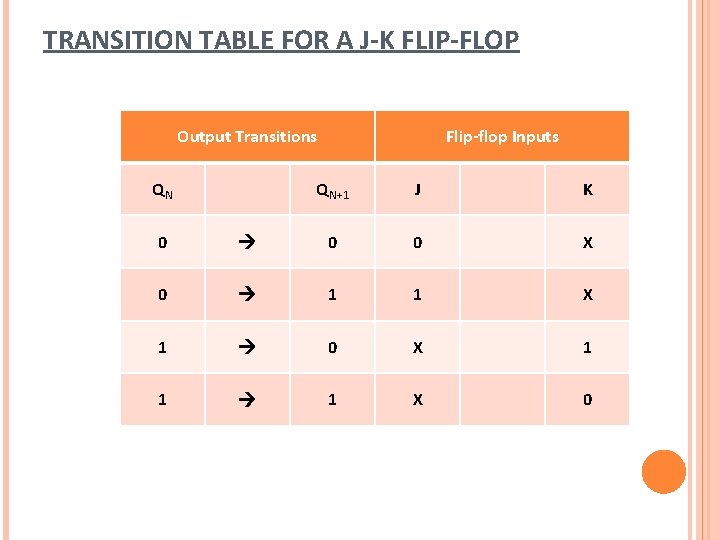
TRANSITION TABLE FOR A J-K FLIP-FLOP Output Transitions QN QN+1 J K 0 0 0 X 0 1 1 X 1 0 X 1 1 1 X 0 QN : present state QN+1: next state X: Don’t care Flip-flop Inputs

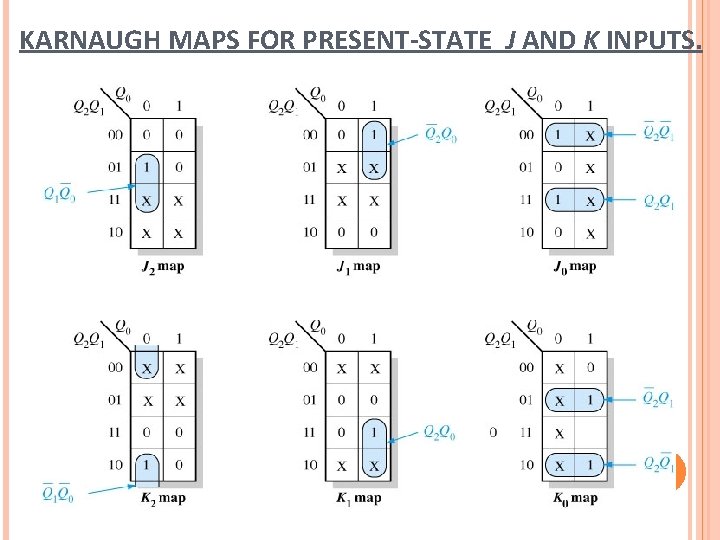
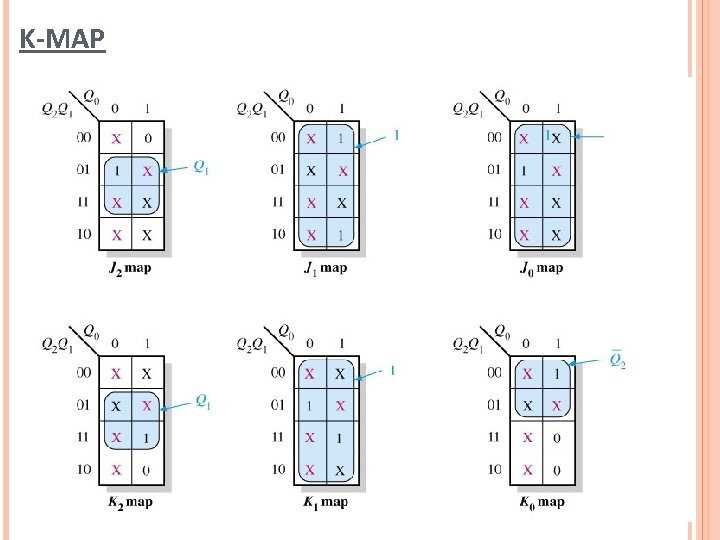
KARNAUGH MAPS FOR PRESENT-STATE J AND K INPUTS.

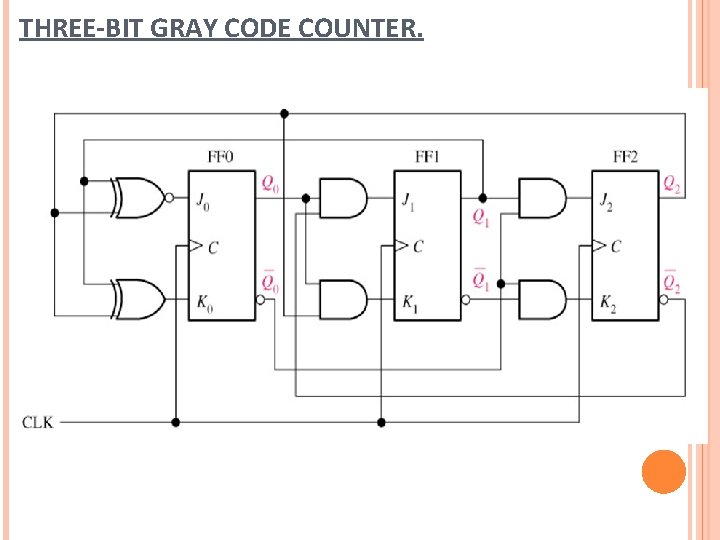
THREE-BIT GRAY CODE COUNTER.

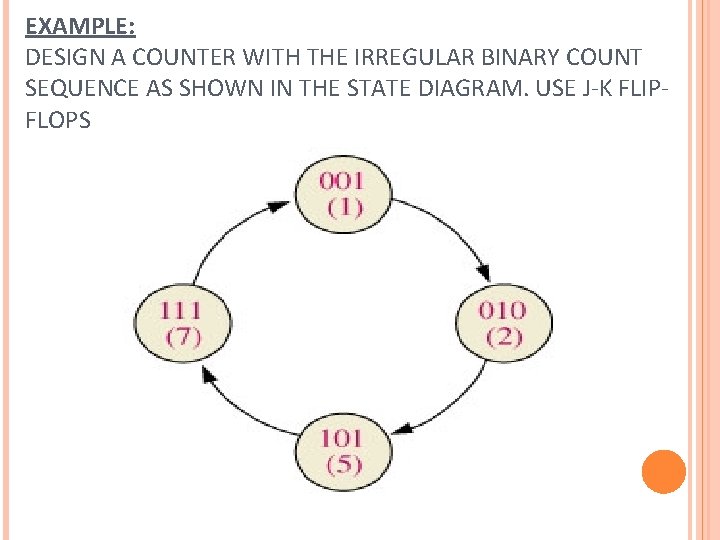
EXAMPLE: DESIGN A COUNTER WITH THE IRREGULAR BINARY COUNT SEQUENCE AS SHOWN IN THE STATE DIAGRAM. USE J-K FLIPFLOPS

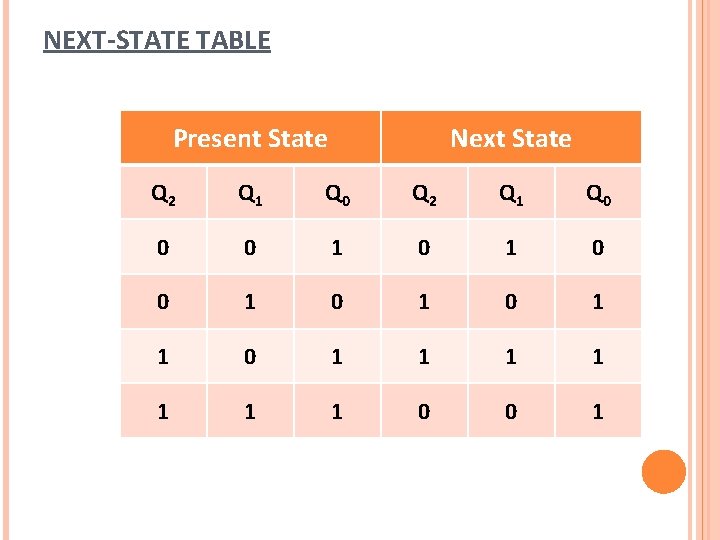
NEXT-STATE TABLE Present State Next State Q 2 Q 1 Q 0 0 0 1 0 1 0 1 1 1 1 1 0 0 1

TRANSITION TABLE FOR A J-K FLIP-FLOP Output Transitions QN Flip-flop Inputs QN+1 J K 0 0 0 X 0 1 1 X 1 0 X 1 1 1 X 0

K-MAP

THE COUNTER CIRCUIT

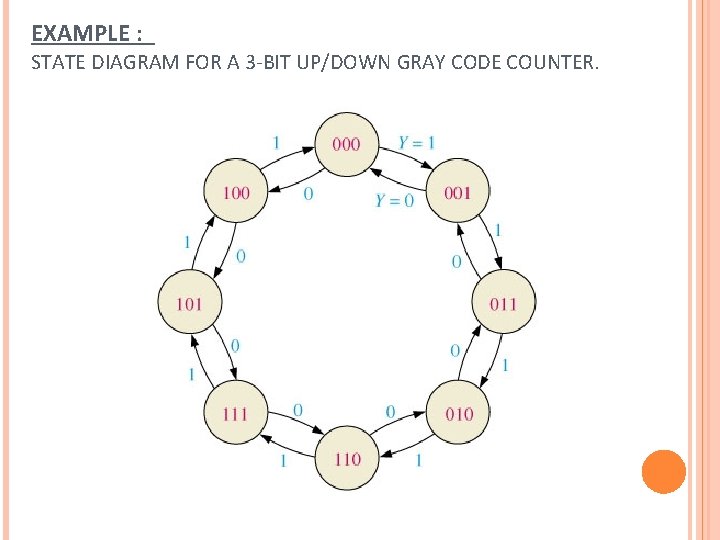
EXAMPLE : STATE DIAGRAM FOR A 3 -BIT UP/DOWN GRAY CODE COUNTER.

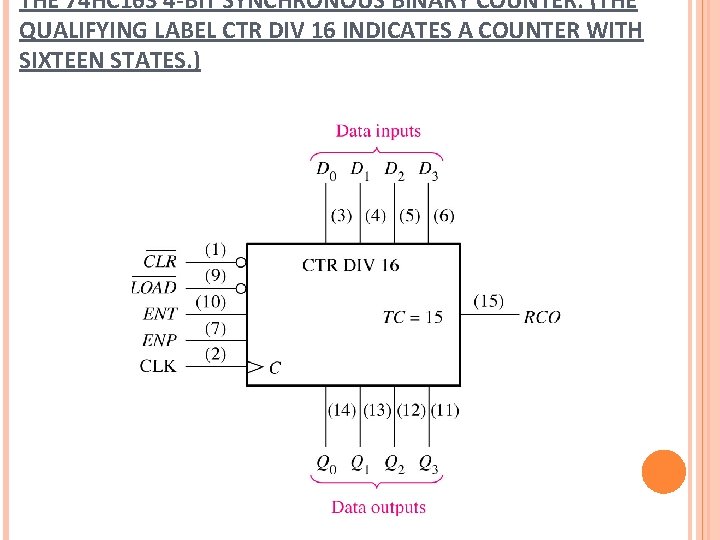
THE 74 HC 163 4 -BIT SYNCHRONOUS BINARY COUNTER. (THE QUALIFYING LABEL CTR DIV 16 INDICATES A COUNTER WITH SIXTEEN STATES. )

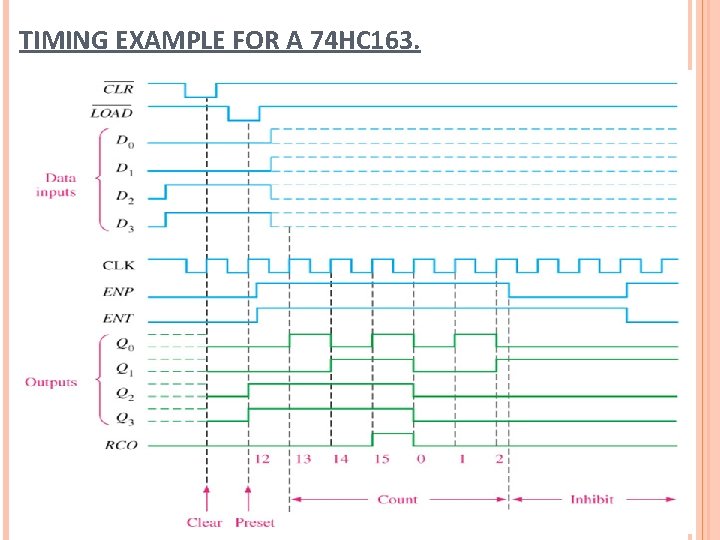
TIMING EXAMPLE FOR A 74 HC 163.

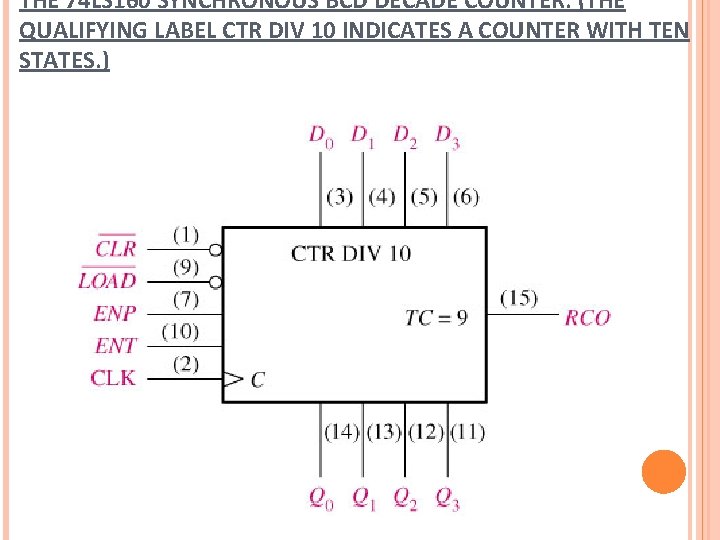
THE 74 LS 160 SYNCHRONOUS BCD DECADE COUNTER. (THE QUALIFYING LABEL CTR DIV 10 INDICATES A COUNTER WITH TEN STATES. )

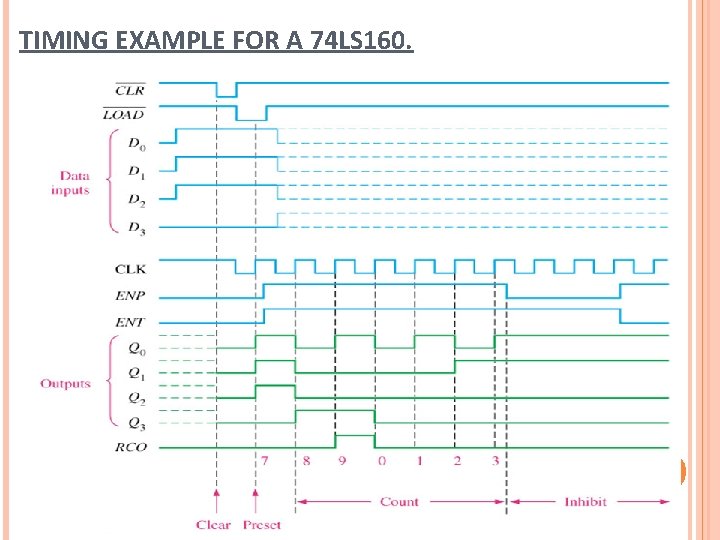
TIMING EXAMPLE FOR A 74 LS 160.

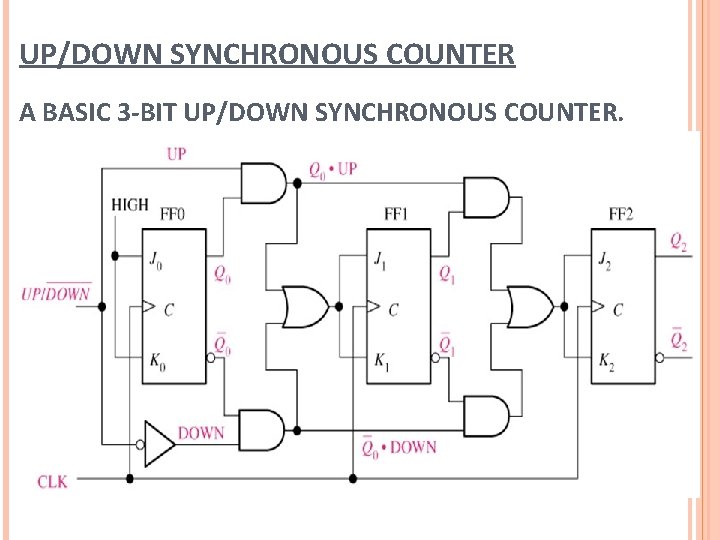
UP/DOWN SYNCHRONOUS COUNTER A BASIC 3 -BIT UP/DOWN SYNCHRONOUS COUNTER.

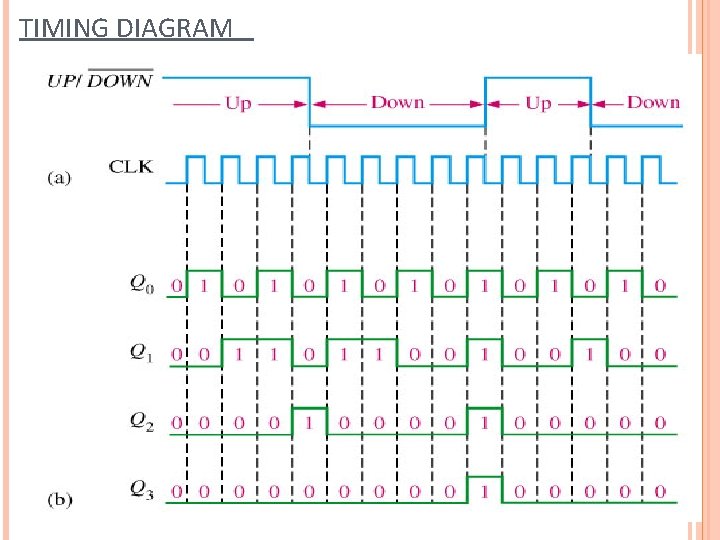
TIMING DIAGRAM

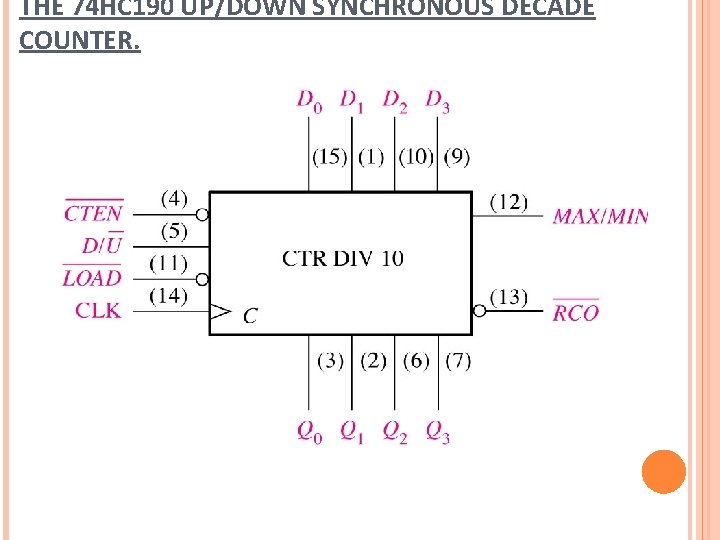
THE 74 HC 190 UP/DOWN SYNCHRONOUS DECADE COUNTER.

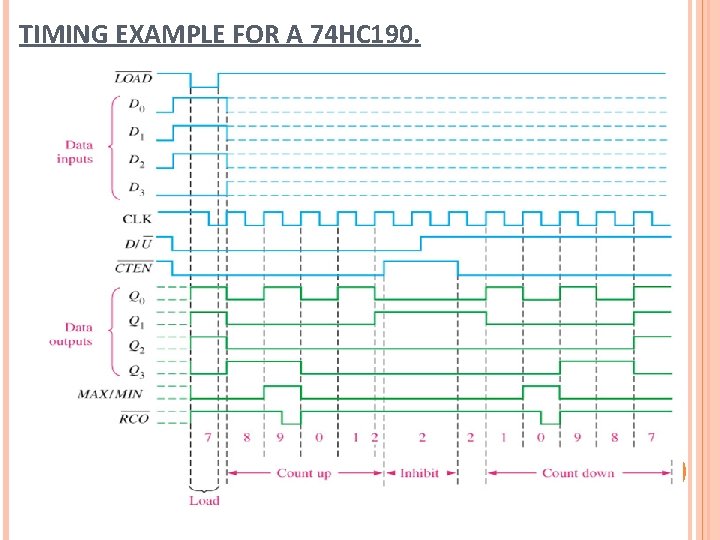
TIMING EXAMPLE FOR A 74 HC 190.

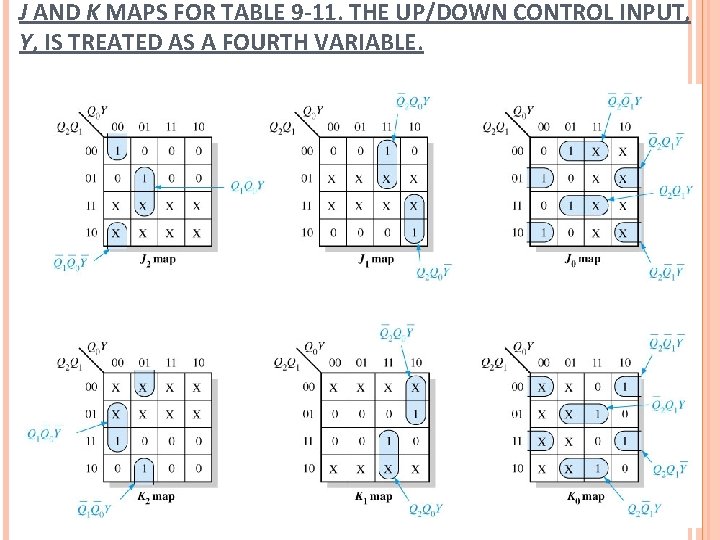
J AND K MAPS FOR TABLE 9 -11. THE UP/DOWN CONTROL INPUT, Y, IS TREATED AS A FOURTH VARIABLE.

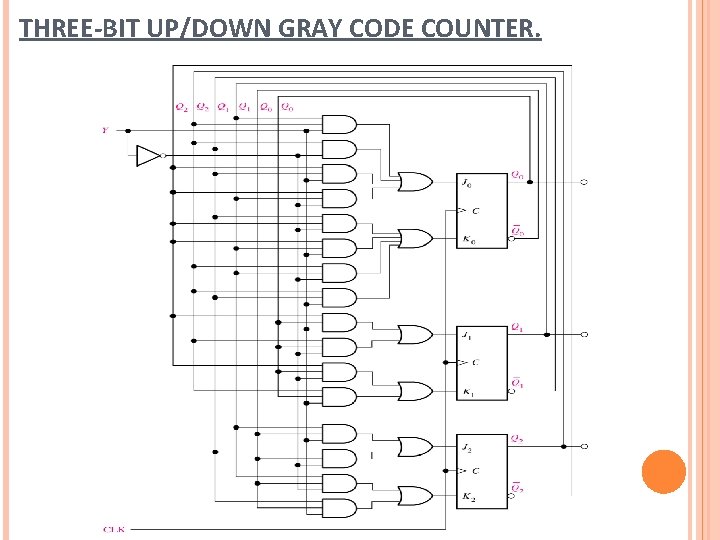
THREE-BIT UP/DOWN GRAY CODE COUNTER.

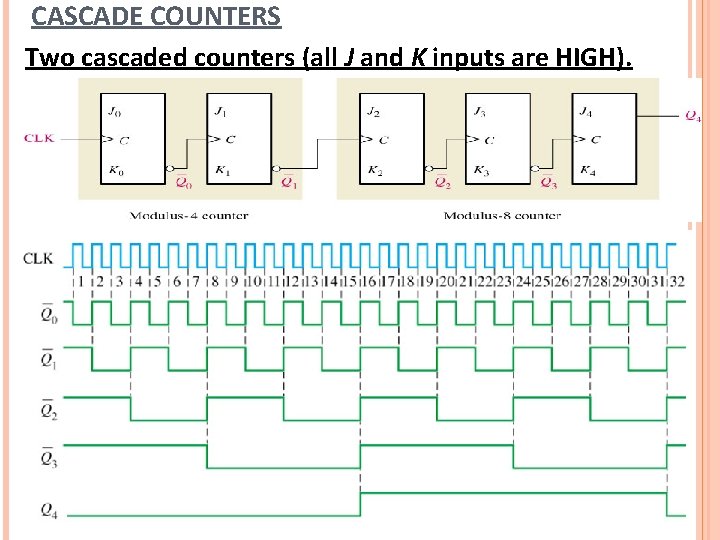
CASCADE COUNTERS Two cascaded counters (all J and K inputs are HIGH).

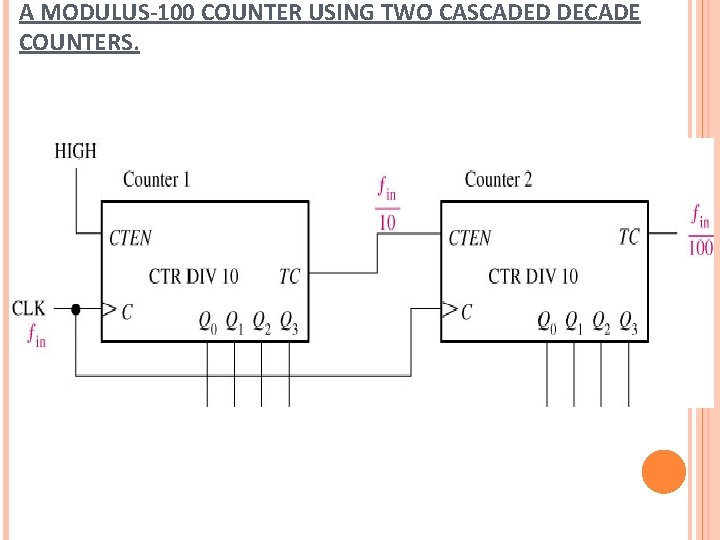
A MODULUS-100 COUNTER USING TWO CASCADED DECADE COUNTERS.

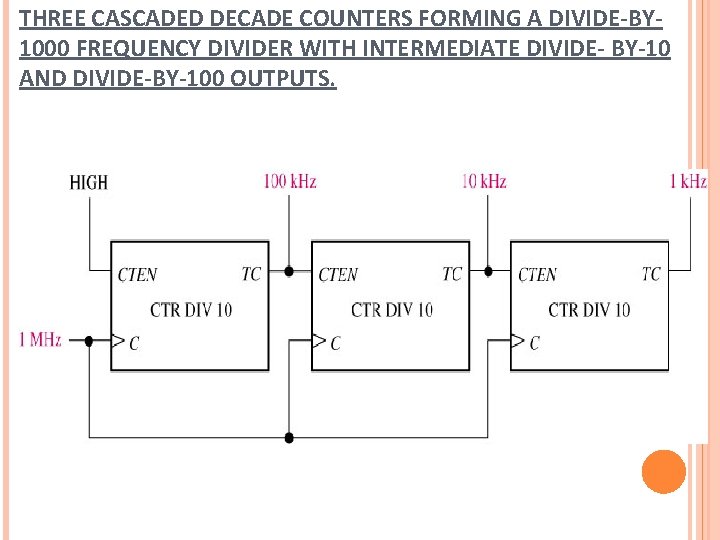
THREE CASCADED DECADE COUNTERS FORMING A DIVIDE-BY 1000 FREQUENCY DIVIDER WITH INTERMEDIATE DIVIDE- BY-10 AND DIVIDE-BY-100 OUTPUTS.

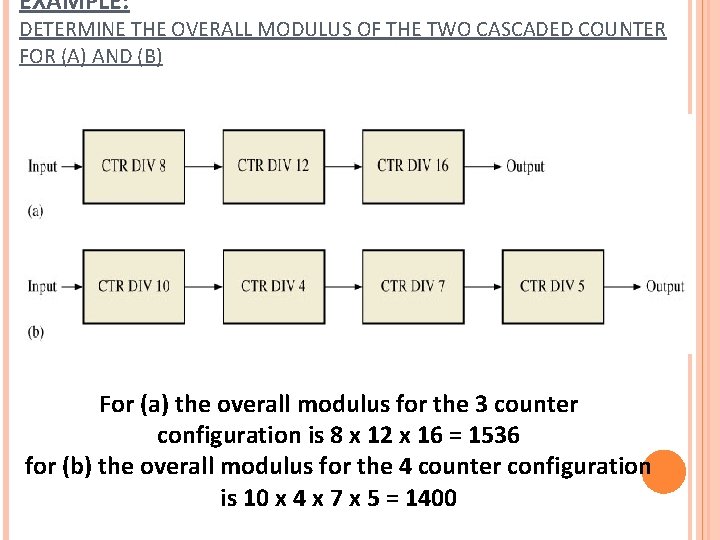
EXAMPLE: DETERMINE THE OVERALL MODULUS OF THE TWO CASCADED COUNTER FOR (A) AND (B) For (a) the overall modulus for the 3 counter configuration is 8 x 12 x 16 = 1536 for (b) the overall modulus for the 4 counter configuration is 10 x 4 x 7 x 5 = 1400

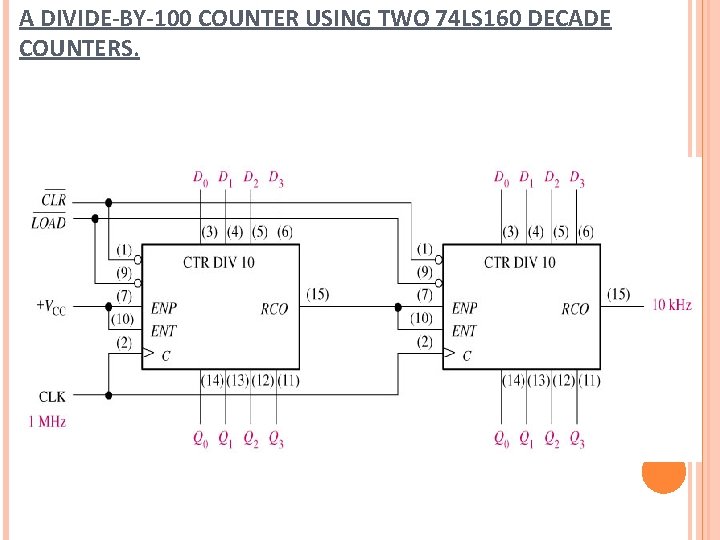
A DIVIDE-BY-100 COUNTER USING TWO 74 LS 160 DECADE COUNTERS.

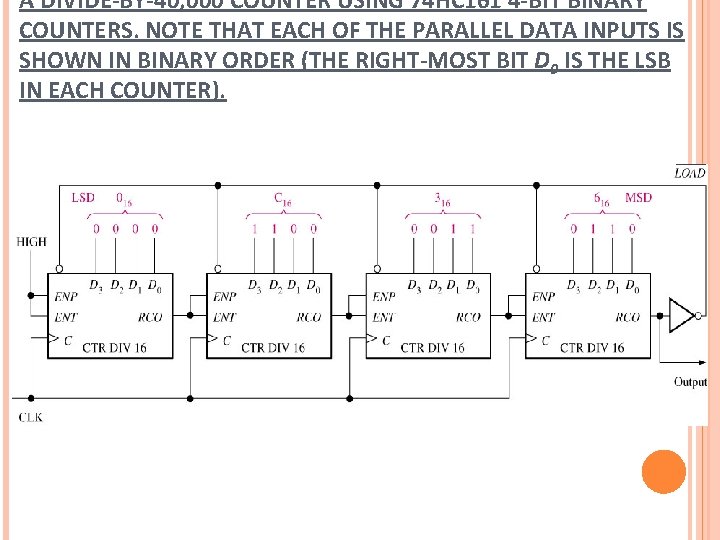
A DIVIDE-BY-40, 000 COUNTER USING 74 HC 161 4 -BIT BINARY COUNTERS. NOTE THAT EACH OF THE PARALLEL DATA INPUTS IS SHOWN IN BINARY ORDER (THE RIGHT-MOST BIT D 0 IS THE LSB IN EACH COUNTER).

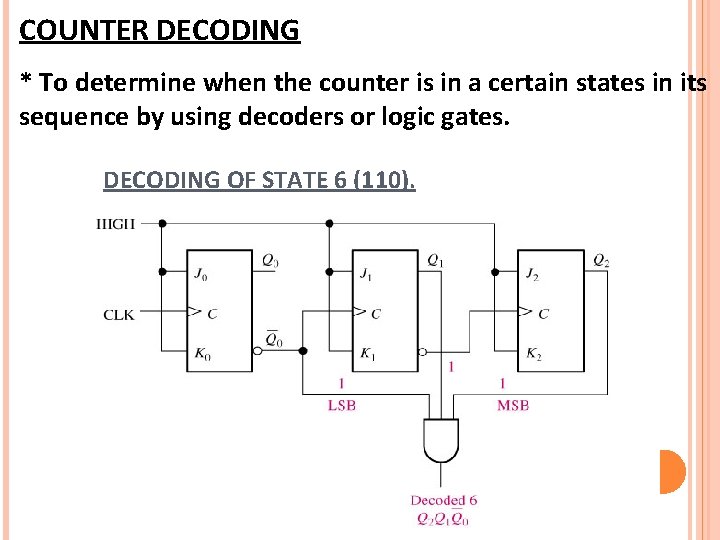
COUNTER DECODING * To determine when the counter is in a certain states in its sequence by using decoders or logic gates. DECODING OF STATE 6 (110).

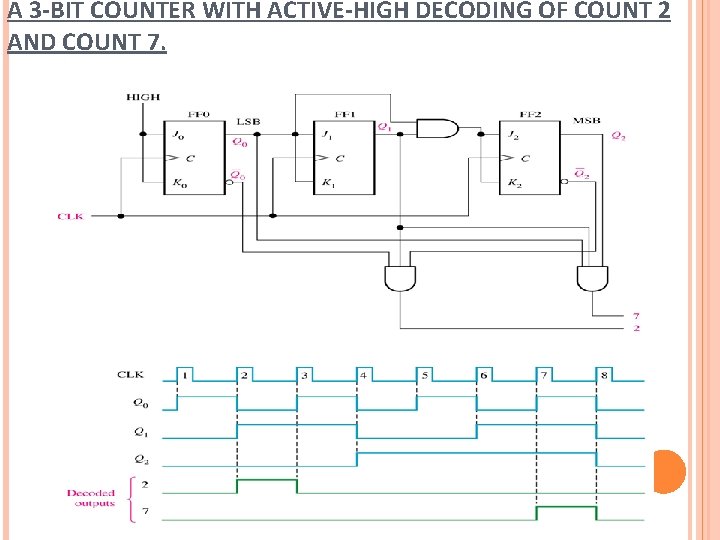
A 3 -BIT COUNTER WITH ACTIVE-HIGH DECODING OF COUNT 2 AND COUNT 7.

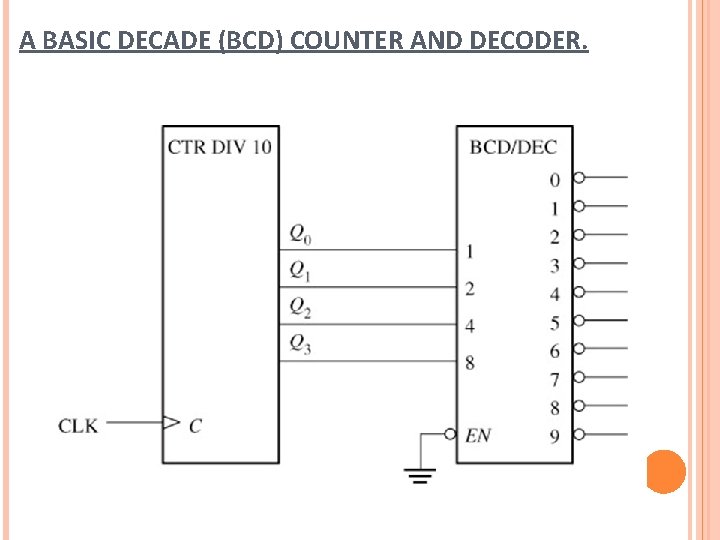
A BASIC DECADE (BCD) COUNTER AND DECODER.

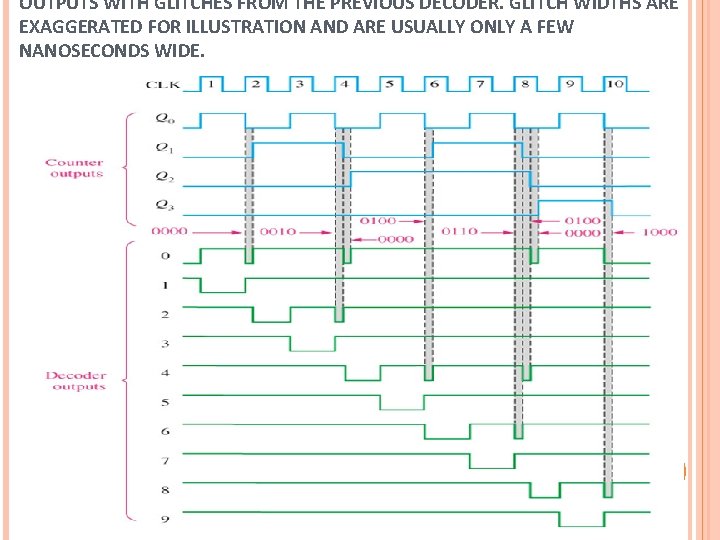
OUTPUTS WITH GLITCHES FROM THE PREVIOUS DECODER. GLITCH WIDTHS ARE EXAGGERATED FOR ILLUSTRATION AND ARE USUALLY ONLY A FEW NANOSECONDS WIDE.

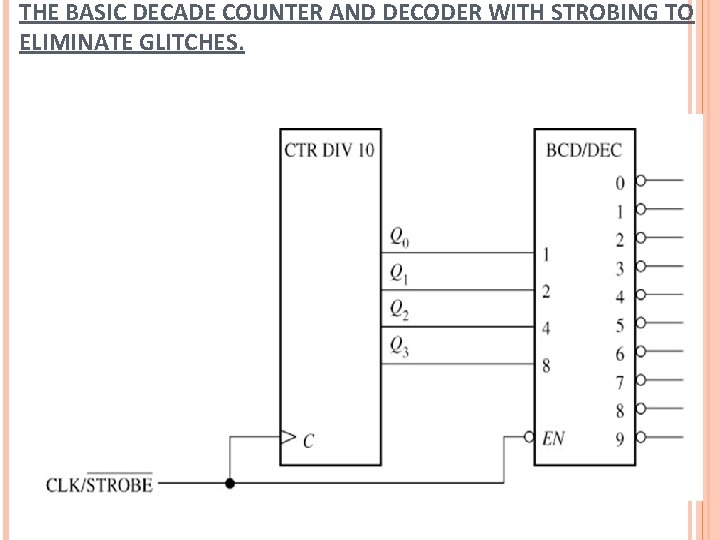
THE BASIC DECADE COUNTER AND DECODER WITH STROBING TO ELIMINATE GLITCHES.

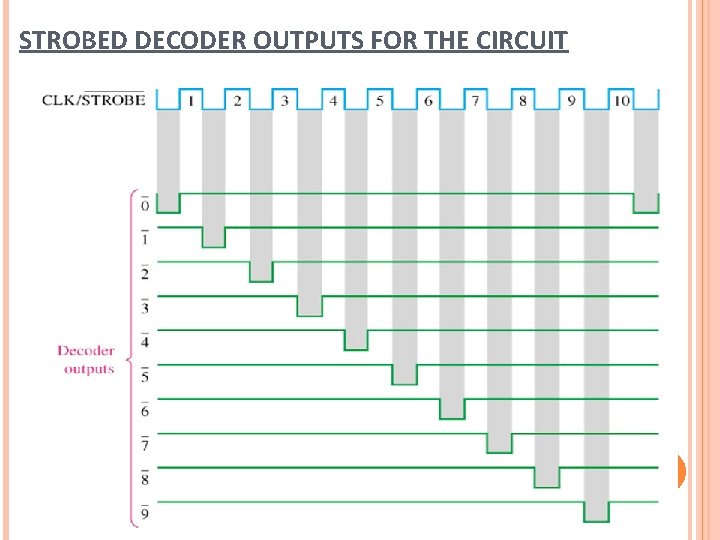
STROBED DECODER OUTPUTS FOR THE CIRCUIT

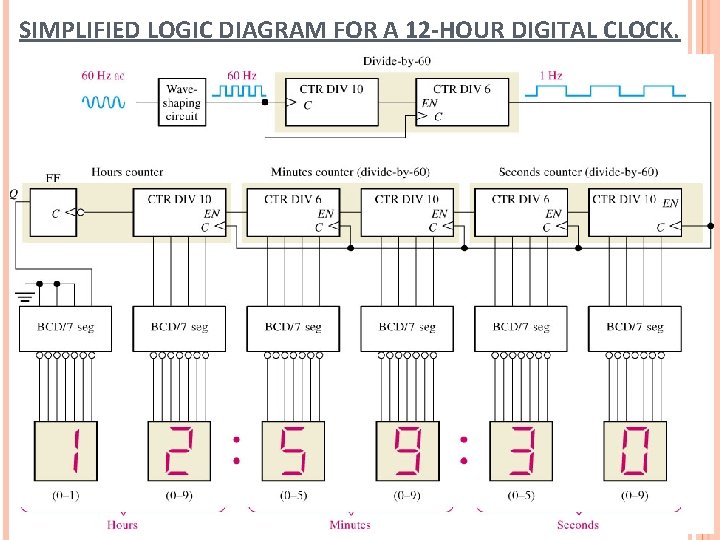
SIMPLIFIED LOGIC DIAGRAM FOR A 12 -HOUR DIGITAL CLOCK.

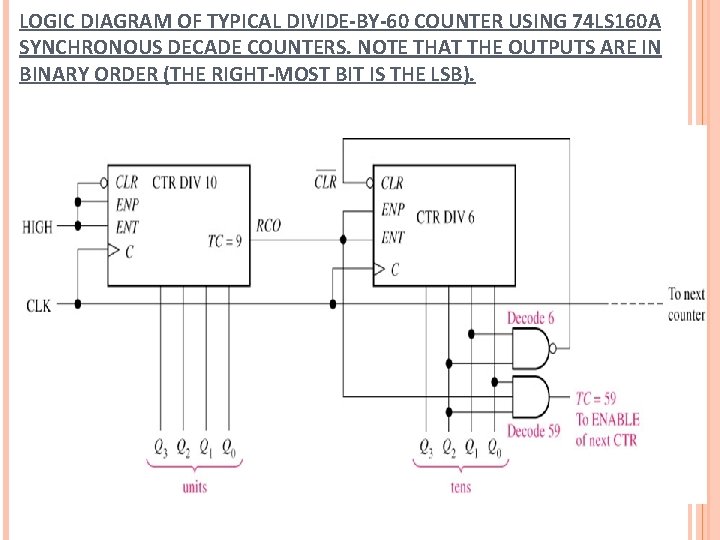
LOGIC DIAGRAM OF TYPICAL DIVIDE-BY-60 COUNTER USING 74 LS 160 A SYNCHRONOUS DECADE COUNTERS. NOTE THAT THE OUTPUTS ARE IN BINARY ORDER (THE RIGHT-MOST BIT IS THE LSB).

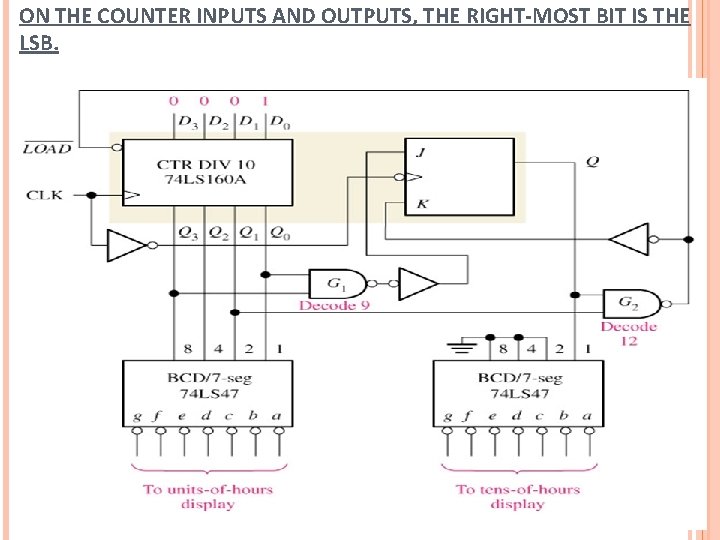
ON THE COUNTER INPUTS AND OUTPUTS, THE RIGHT-MOST BIT IS THE LSB.

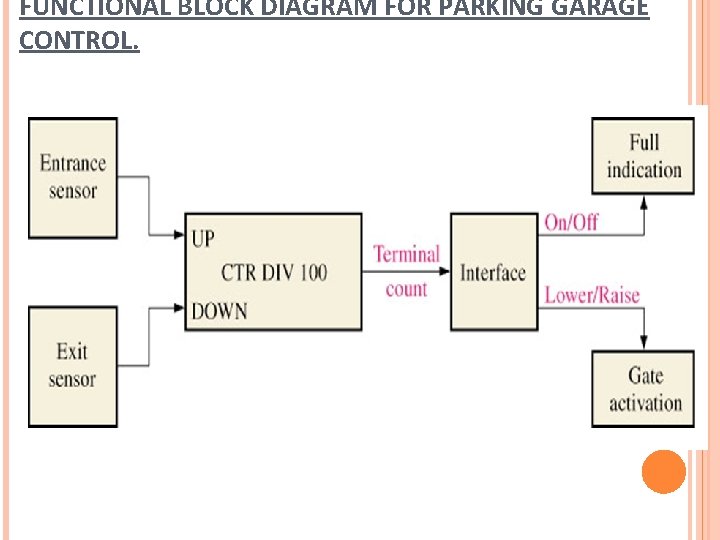
FUNCTIONAL BLOCK DIAGRAM FOR PARKING GARAGE CONTROL.

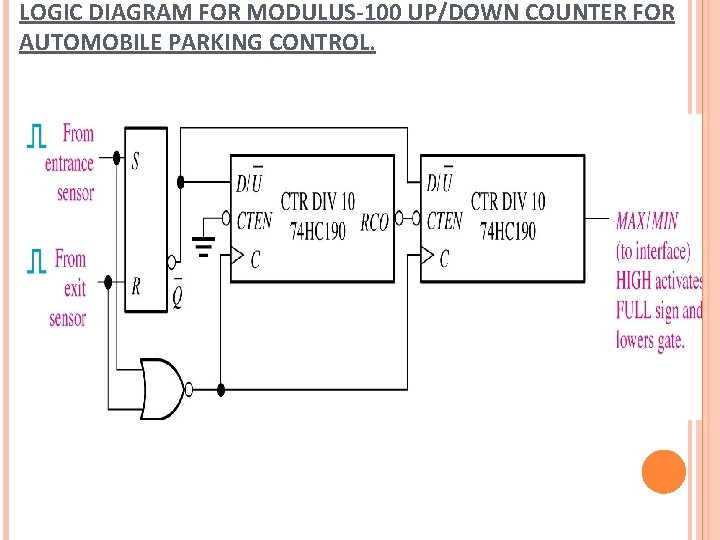
LOGIC DIAGRAM FOR MODULUS-100 UP/DOWN COUNTER FOR AUTOMOBILE PARKING CONTROL.

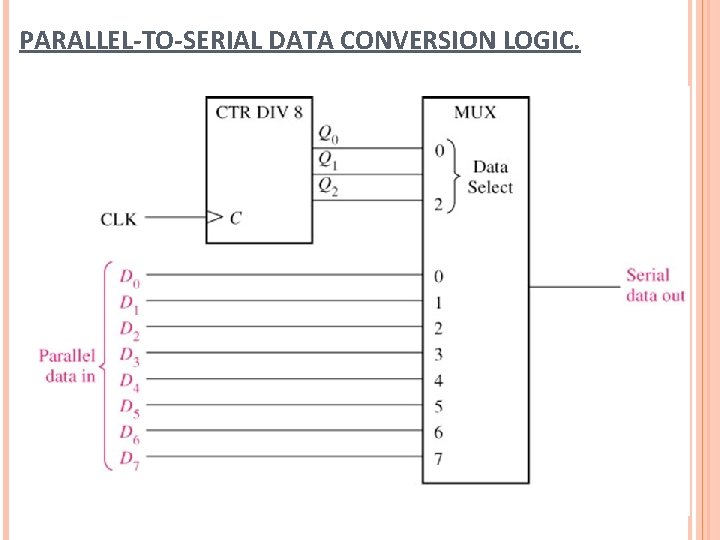
PARALLEL-TO-SERIAL DATA CONVERSION LOGIC.

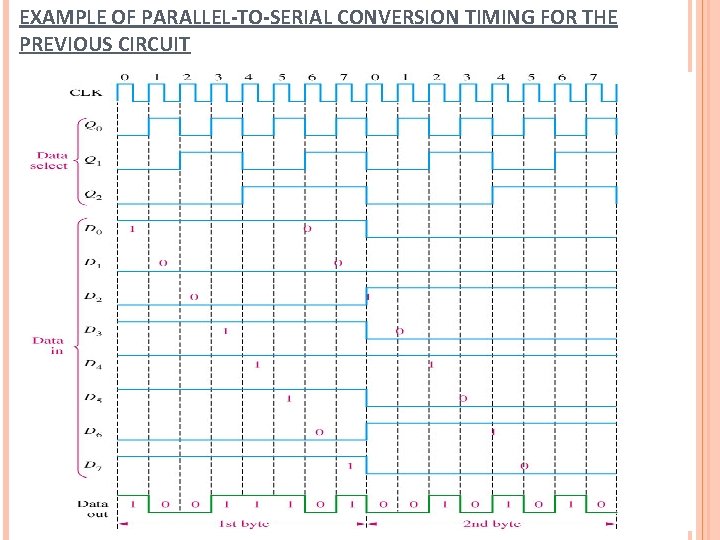
EXAMPLE OF PARALLEL-TO-SERIAL CONVERSION TIMING FOR THE PREVIOUS CIRCUIT

THANK YOU