EET 1073 DIGITAL ELECTRONICS 1 Chapter 2 Combinational

EET 107/3 DIGITAL ELECTRONICS 1 Chapter 2: Combinational Logic Circuit (Part 1)

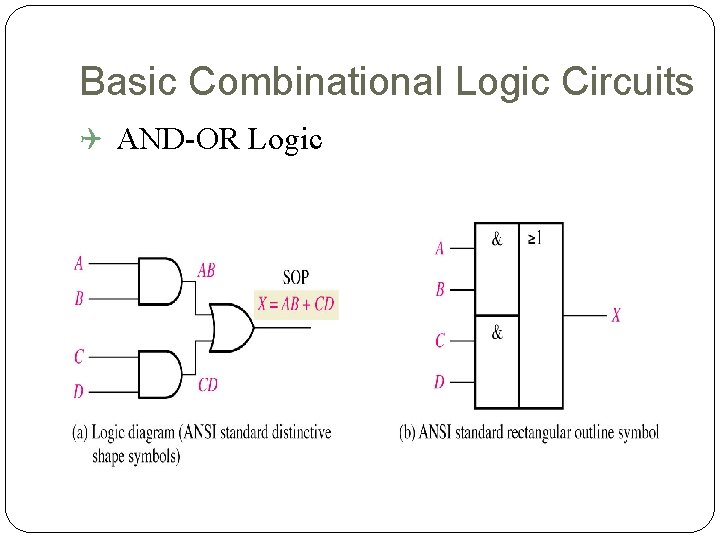
Basic Combinational Logic Circuits AND-OR Logic

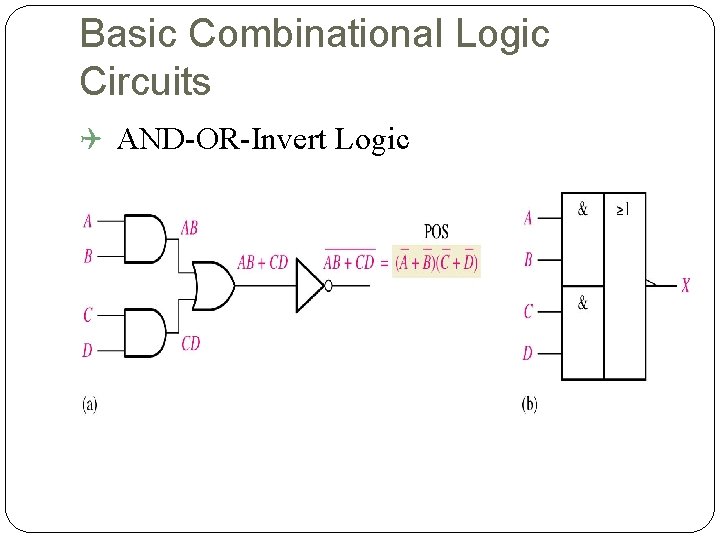
Basic Combinational Logic Circuits AND-OR-Invert Logic

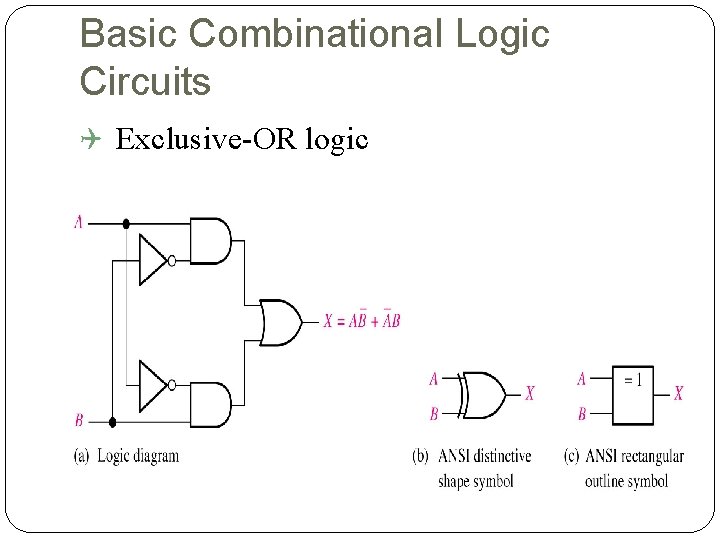
Basic Combinational Logic Circuits Exclusive-OR logic

Basic Combinational Logic Circuits Exclusive-NOR logic

Basic Combinational Logic Circuits Exclusive-NOR Equation

2. 1 Digital Arithmetic Binary arithmetic complement representation complement arithmetic Hexadecimal arithmetic BCD arithmetic Arithmetic circuits Half Adder/Subtractor 4 -bit full-adder/subtractor ICs

Binary Arithmetic - Addition Two binary numbers are performed in exactly the same manner as the addition of decimal numbers. Addition Example: X 229 Y + 46 275 1 1 1 0 0 1 + 0 0 1 1 1 0 0 0 1 1

Binary Subtraction Two binary numbers are subtracted by subtracting each pair of bits together with borrowing, where needed. Subtraction Example: X 229 Y - 46 183 - 1 1 1 0 0 1 0 1 1 0 1 1 1

Complements Allow the representation of negative numbers. Complements are used in digital computers for simplifying the subtraction operation. Two types of complement for binary numbers: o One’s complement o Two’s complement The 1’s complement of a binary number is formed by changing 1’s to 0’s and 0’s to 1’s Example: 1. The 1’s complement of 1011000 is 0100111 2. The 1’s complement of 0101101 is 1010010

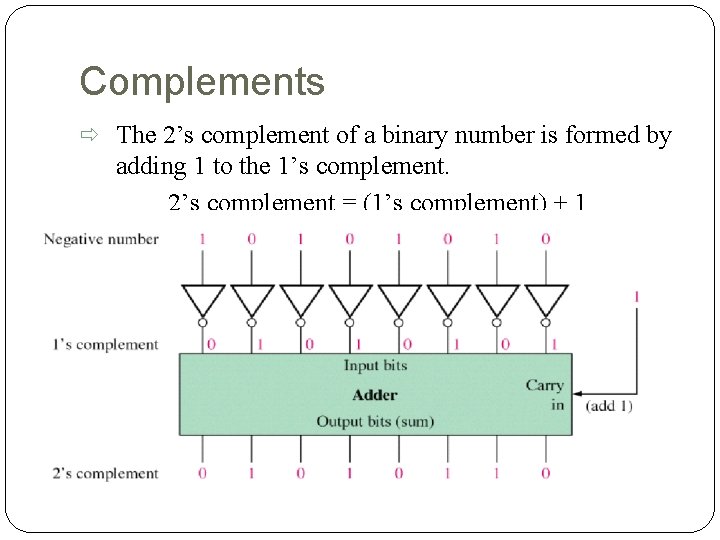
Complements The 2’s complement of a binary number is formed by adding 1 to the 1’s complement. 2’s complement = (1’s complement) + 1

Complements Alternative method to find 2’s complement: o Start at the right with the LSB and write the bits as they are up to including the first 1. o Do 1’s complements of the remaining bits. Example: 1. The 2’s complement of 1101100 is 0010100 2. The 2’s complement of 0110111 is 1001001

Negative Binary Number Representations Signed-Magnitude Representation: o For an n-bit binary number: Use the first bit (most significant bit, MSB) position to represent the sign where 0 is positive and 1 is negative. Ex. 1 Magnitude 1 1 12 = - 12710 Sign o Remaining n-1 bits represent the magnitude which may range from: -2(n-1) + 1 to 2(n-1) – 1 o This scheme has two representations for 0; i. e. , both positive and negative 0: for 8 bits: 0000, 10000000 o Arithmetic under this scheme uses the sign bit to indicate the nature of the operation and the sign of the result, but

Combinational Arithmetic Circuits Addition: o Half Adder (HA) o Full Adder (FA) o Carry Ripple Adders Subtraction: o Half Subtractor o Full Subtractor o Borrow Ripple Subtractors o Subtraction using adders

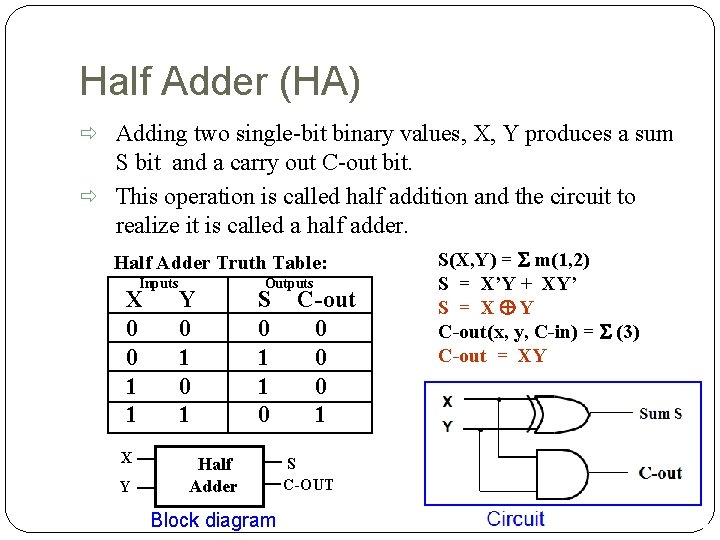
Half Adder (HA) Adding two single-bit binary values, X, Y produces a sum S bit and a carry out C-out bit. This operation is called half addition and the circuit to realize it is called a half adder. Half Adder Truth Table: Inputs X 0 0 1 1 X Y Y 0 1 Outputs S 0 1 1 0 Half Adder Block diagram C-out 0 0 0 1 S C-OUT S(X, Y) = S m(1, 2) S = X’Y + XY’ S = XÅY C-out(x, y, C-in) = S (3) C-out = XY

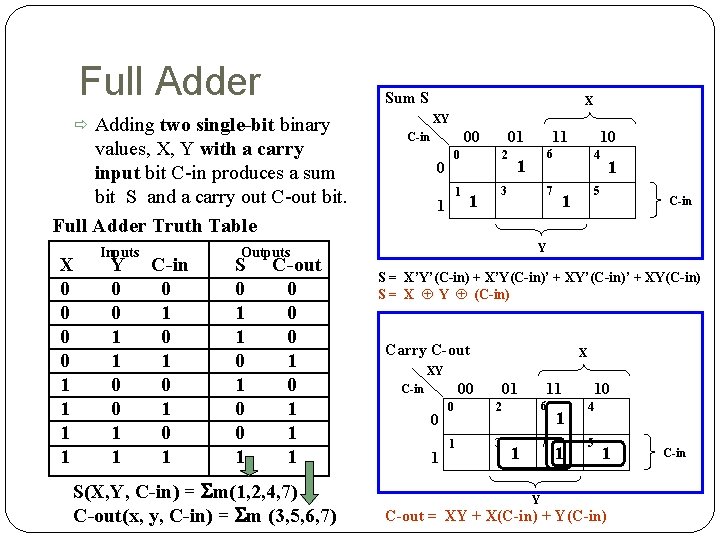
Full Adder Sum S Adding two single-bit binary values, X, Y with a carry input bit C-in produces a sum bit S and a carry out C-out bit. Full Adder Truth Table X 0 0 1 1 Inputs Y 0 0 1 1 C-in 0 1 0 1 X XY 00 C-in 01 0 0 1 1 2 3 1 C-out 0 0 0 1 1 1 S(X, Y, C-in) = Sm(1, 2, 4, 7) C-out(x, y, C-in) = Sm (3, 5, 6, 7) 10 6 1 4 7 1 5 1 C-in Y Outputs S 0 1 1 0 0 1 11 S = X’Y’(C-in) + X’Y(C-in)’ + XY’(C-in)’ + XY(C-in) S = X Å Y Å (C-in) Carry C-out X XY 00 C-in 0 1 01 0 2 1 3 11 6 7 1 10 4 5 1 Y C-out = XY + X(C-in) + Y(C-in) C-in

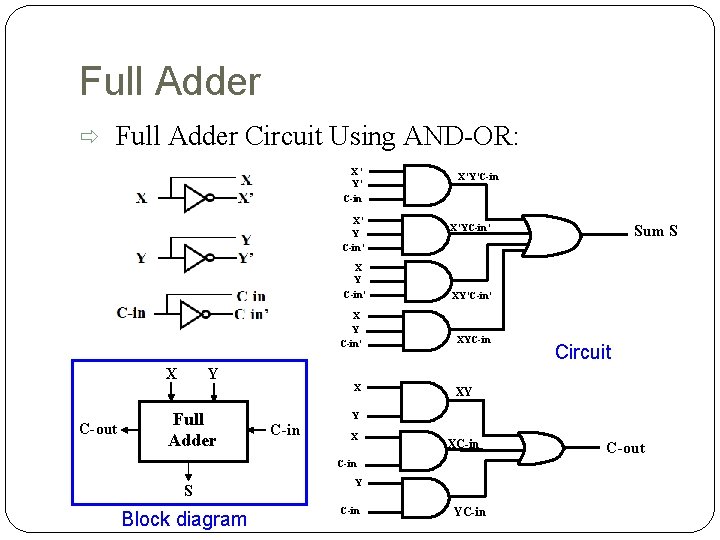
Full Adder Circuit Using AND-OR: X’ Y’ C-in X’ Y C-in’ X’Y’C-in Sum S X’YC-in’ X Y C-in’ X C-out Y Full Adder X XY’C-in’ XYC-in XY Y C-in X XC-in S Block diagram Circuit Y C-in YC-in C-out

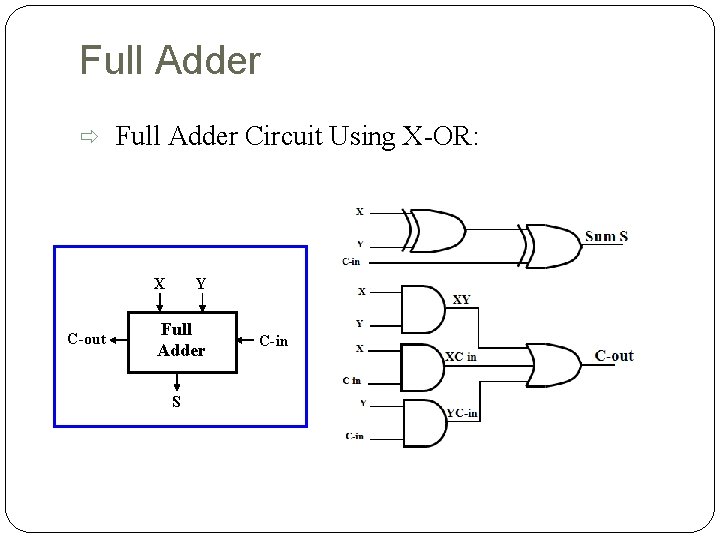
Full Adder Circuit Using X-OR: X C-out Y Full Adder S C-in

n-bit Carry Ripple Adders An n-bit adder used to add two n-bit binary numbers can built by connecting in series n full adders. o Each full adder represents a bit position j (from 0 to n-1). o Each carry out C-out from a full adder at position j is connected to the carry in C-in of the full adder at the higher position j+1. The output of a full adder at position j is given by: Sj = X j Å Yj Å C j Cj+1 = Xj. Yj + Xj. Cj + Y. Cj In the expression of the sum Cj must be generated by the full adder at the lower position j-1. The propagation delay in each full adder to produce the carry is equal to two gate delays = 2 D Since the generation of the sum requires the propagation of the carry from the lowest position to the highest position , the total propagation delay of the adder is approximately: Total Propagation delay = 2 n. D

4 -bit Carry Ripple Adder Inputs to be added Adds two 4 -bit numbers: X = X 3 X 2 X 1 X 0 Y = Y 3 Y 2 Y 1 Y 0 producing the sum S = S 3 S 2 S 1 S 0 , C-out = C 4 from the most significant position j=3 Total Propagation delay or 8 gate delays X 3 X 2 X 1 X 0 C 4 C-out Y 3 Y 2 Y 1 Y 0 4 -bit Adder C-in C 0 =0 = 2 n. D = 8 D S 3 S 2 S 1 S 0 Sum Output Data inputs to be added X 3 C 4 C-out Y 3 Full C 3 C-in Adder S 3 X 2 C-out Y 2 Full C 2 C-in Adder X 1 C-out S 2 Full C-in Adder S 1 Sum output X 0 Y 1 C-out Y 0 Full C-in Adder S 0 C 0 =0

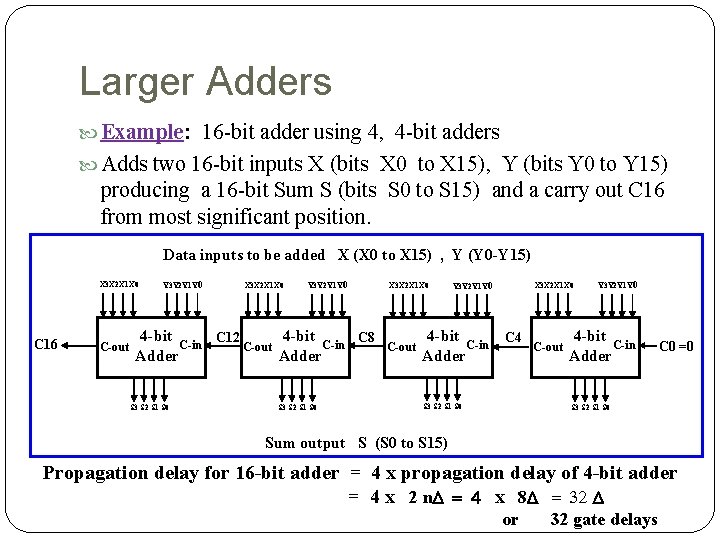
Larger Adders Example: 16 -bit adder using 4, 4 -bit adders Adds two 16 -bit inputs X (bits X 0 to X 15), Y (bits Y 0 to Y 15) producing a 16 -bit Sum S (bits S 0 to S 15) and a carry out C 16 from most significant position. Data inputs to be added X (X 0 to X 15) , Y (Y 0 -Y 15) X 3 X 2 X 1 X 0 C 16 C-out Y 3 Y 2 Y 1 Y 0 X 3 X 2 X 1 X 0 Y 3 Y 2 Y 1 Y 0 4 -bit C 12 C 8 C-in C-out Adder S 3 S 2 S 1 S 0 X 3 X 2 X 1 X 0 C-out Y 3 Y 2 Y 1 Y 0 4 -bit C-in Adder X 3 X 2 X 1 X 0 C 4 S 3 S 2 S 1 S 0 C-out Y 3 Y 2 Y 1 Y 0 4 -bit C-in Adder C 0 =0 S 3 S 2 S 1 S 0 Sum output S (S 0 to S 15) Propagation delay for 16 -bit adder = 4 x propagation delay of 4 -bit adder = 4 x 2 n. D = 4 x 8 D = 32 D or 32 gate delays

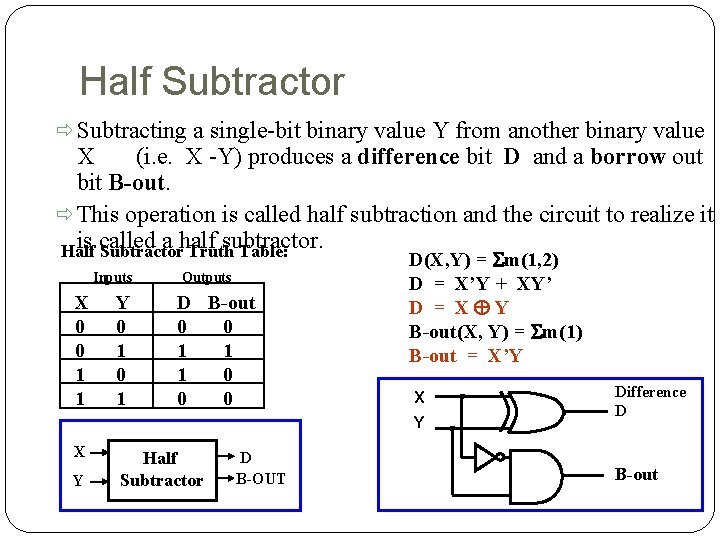
Half Subtractor Subtracting a single-bit binary value Y from another binary value X (i. e. X -Y) produces a difference bit D and a borrow out bit B-out. This operation is called half subtraction and the circuit to realize it is called a half subtractor. Half Subtractor Truth Table: Inputs X 0 0 1 1 Y 0 1 Outputs D B-out 0 0 1 1 1 0 0 0 D(X, Y) = Sm(1, 2) D = X’Y + XY’ D = XÅY B-out(X, Y) = Sm(1) B-out = X’Y X Y Half Subtractor D B-OUT Difference D B-out

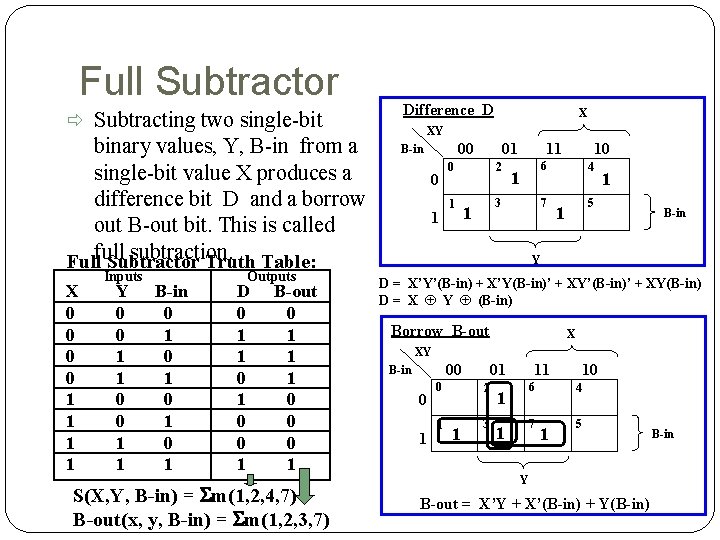
Full Subtractor Subtracting two single-bit binary values, Y, B-in from a single-bit value X produces a difference bit D and a borrow out B-out bit. This is called subtraction. Fullfull Subtractor Truth Table: X 0 0 1 1 Inputs Y 0 0 1 1 B-in 0 1 0 1 Outputs D 0 1 1 0 0 1 B-out 0 1 1 1 0 0 0 1 S(X, Y, B-in) = Sm(1, 2, 4, 7) B-out(x, y, B-in) = Sm(1, 2, 3, 7) Difference D X XY 00 B-in 0 1 01 0 1 2 11 6 1 3 1 10 7 4 1 5 1 B-in Y D = X’Y’(B-in) + X’Y(B-in)’ + XY’(B-in)’ + XY(B-in) D = X Å Y Å (B-in) Borrow B-out X XY 00 B-in 0 1 01 2 1 3 11 6 1 7 1 10 4 1 5 Y B-out = X’Y + X’(B-in) + Y(B-in) B-in

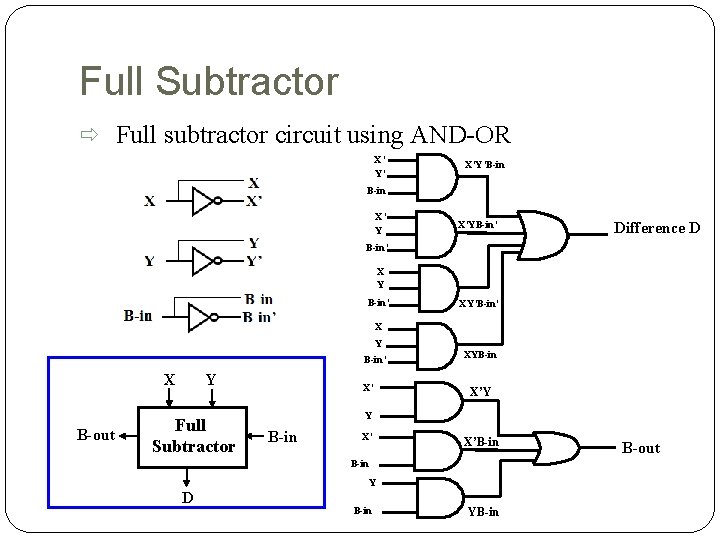
Full Subtractor Full subtractor circuit using AND-OR X’ Y’ X’Y’B-in X’ Y X’YB-in’ Difference D B-in’ X Y B-in’ XY’B-in’ X Y B-in’ X B-out Y Full Subtractor X’ XYB-in X’Y Y B-in X’ X’B-in Y D B-in YB-in B-out

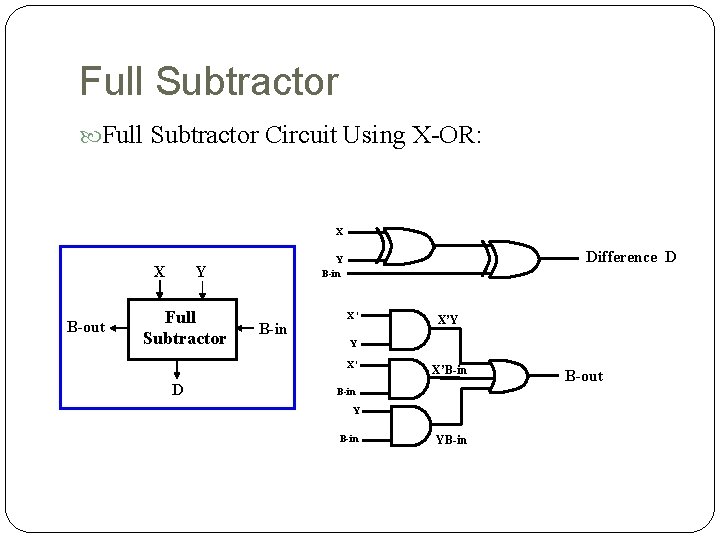
Full Subtractor Circuit Using X-OR: X X B-out Y Full Subtractor Difference D Y B-in X’ Y X’ D X’Y X’B-in YB-in B-out

n-bit Borrow Ripple Subtractor An n-bit subtractor used to subtract an n-bit number Y from another n-bit number X (i. e X-Y) can be built in one of two ways: By using n full subtractors and connecting them in series, creating a borrow ripple subtractor: o Each borrow out B-out from a full subtractor at position j is connected to the borrow in B-in of the full subtractor at the higher position j+1. By using an n-bit adder and n inverters: o Find 2’s complement of Y by: ü Inverting all the bits of Y using the n inverters. ü Adding 1 by setting the carry in of the least significant position to 1 o The original subtraction (X - Y) now becomes an addition of X to two’s complement of Y using the n-bit adder.

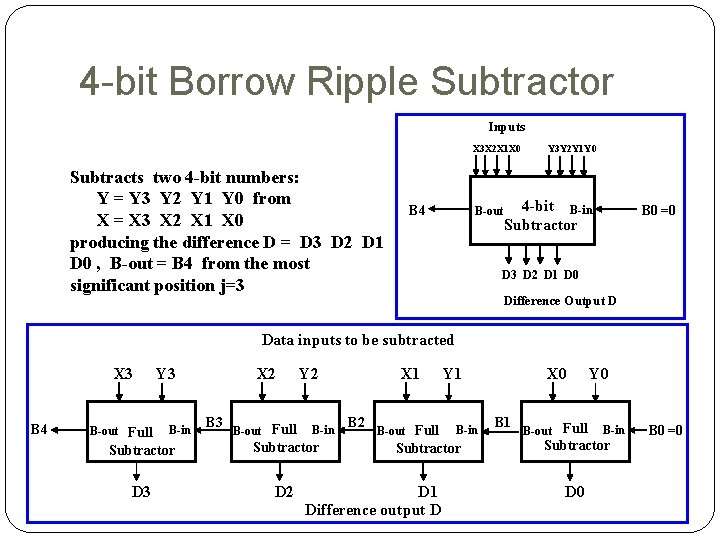
4 -bit Borrow Ripple Subtractor Inputs X 3 X 2 X 1 X 0 Subtracts two 4 -bit numbers: Y = Y 3 Y 2 Y 1 Y 0 from X = X 3 X 2 X 1 X 0 producing the difference D = D 3 D 2 D 1 D 0 , B-out = B 4 from the most significant position j=3 B 4 B-out Y 3 Y 2 Y 1 Y 0 4 -bit B-in Subtractor B 0 =0 D 3 D 2 D 1 D 0 Difference Output D Data inputs to be subtracted X 3 B 4 B-out Full Y 3 B-in X 2 B 3 B-out Full Y 2 B-in Subtractor D 3 D 2 X 1 B 2 B-out Full Y 1 B-in Subtractor D 1 Difference output D X 0 B 1 B-out Full Y 0 B-in Subtractor D 0 B 0 =0

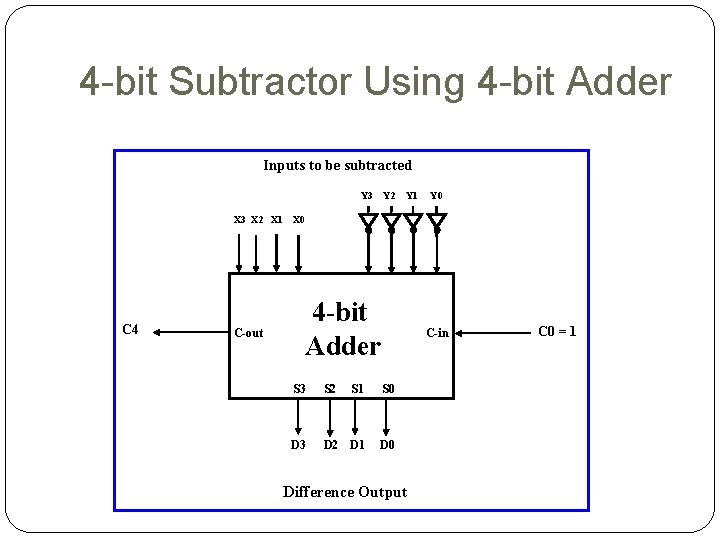
4 -bit Subtractor Using 4 -bit Adder Inputs to be subtracted Y 3 X 2 X 1 C 4 C-out Y 2 Y 1 Y 0 X 0 4 -bit Adder C-in S 3 S 2 S 1 S 0 D 3 D 2 D 1 D 0 Difference Output C 0 = 1