EEG analysis during hypnagogium Petr Svoboda Laboratory of

EEG analysis during hypnagogium Petr Svoboda Laboratory of System Reliability Faculty of Transportation Czech Technical University e-mail: svobodap@spel. cz

Presented methods ü Traditional methods Fourier transform ü Parametrical methods Autoregressive estimator ü Nonlinear methods - Chaos theory Delay-time embedding, Correlation dimension, Takens estimator, State Space dimension, Lyapunov exponents

EEG activity ü electric potential of brain‘s neural activity ü registered on the skelet ü four basic frequencies

Traditional methods Estimate of a periodogram using the Fourier transform Potencial problems ü Signal‘s stationarity ü frequency resolution ü leakage of frequency spectra ü quality of the spectral estimate ü phase of the signal is lost

Parametric model Approximation of an EEG signal by adequate parametric model Autoregressive (AR) model: Approximation of an EEG signal by linear time invariant filter with transfer function H(z)=1/A(z) Whitening of signal by AR filter:

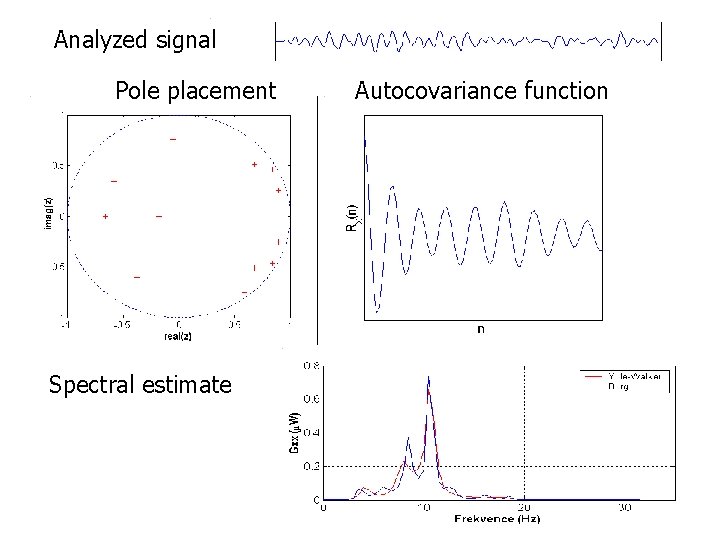
Analyzed signal Pole placement Spectral estimate Autocovariance function

Comparison of traditional and parametric methods Traditional methods: + low noise sensitivity - frequency resolution Parametric methods: + frequency resolution + parametric description of analyzed signal - estimate of AR model order - high noise sensitivity

Microsleep classification Traditional methods + Alpha, deltha and theta activity of spectral estimate Parametrical methods + Alpha, deltha and theta activity of spectral estimate - estimate of AR model order - placement of poles in a complex plane

Classification by spectral estimate ü Classification into 2 states • RELAXATION • DROWSINESS ü Classification based on neural network (back propagation) ü Classical methods: accuracy of about 87% ü Parametrical methods: accuracy of about 90%

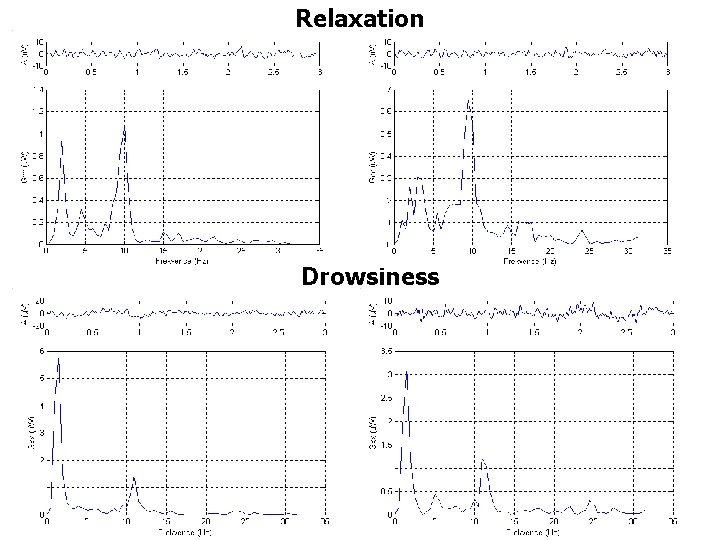
Relaxation Drowsiness

Chaos theory ü analysis of dynamic deterministic systems • high sensitivity on initial conditions • known dynamics and phase of the system ü detecting nonlinearity by surrogate data testing ü delay-time embedding • state-space dimension estimate • estimate of delay time ü estimate of fractal dimension D 2 ü Takens estimator for D 2 dimension ü largest Lyapunov exponents

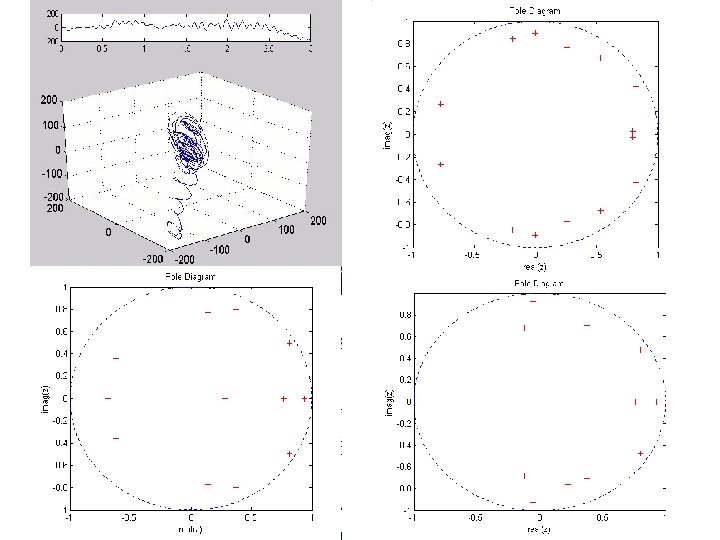
Delay-time embedding Si=[x(i), x(i+L), … x(i+(m-1)L)] L… time delay Si… state-space vector m… state dimension x… analyzed signal

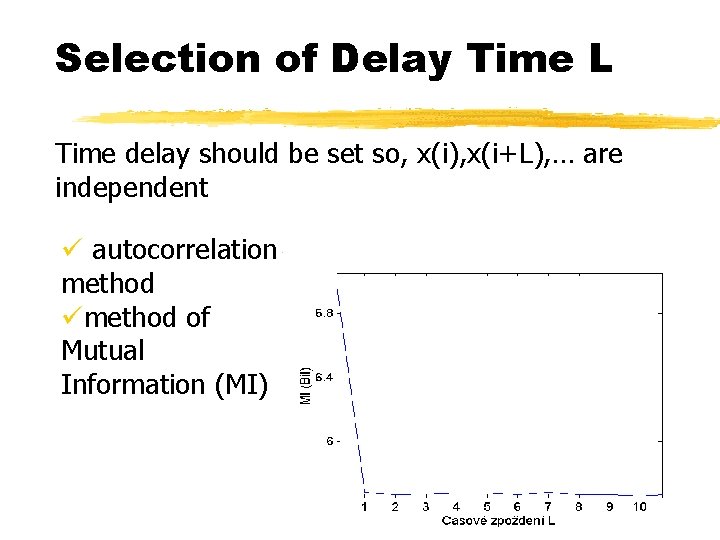
Selection of Delay Time L Time delay should be set so, x(i), x(i+L), … are independent ü autocorrelation method ümethod of Mutual Information (MI)

Fractal dimension & Takens estimator Fractal dimension is a measure of complexity of the analyzed signal D 2 = log C(r) / log r Where C(r) is correlation integral D 2 computed by maximum likelihood estimator is known as Takens estimator

Microsleep classification Chaos theory + matematical description of state-space trajectory reconstruction nonlinearity detection - correlation dimension D 2 estimate + Takens estimator + largest Lyapunov exponents

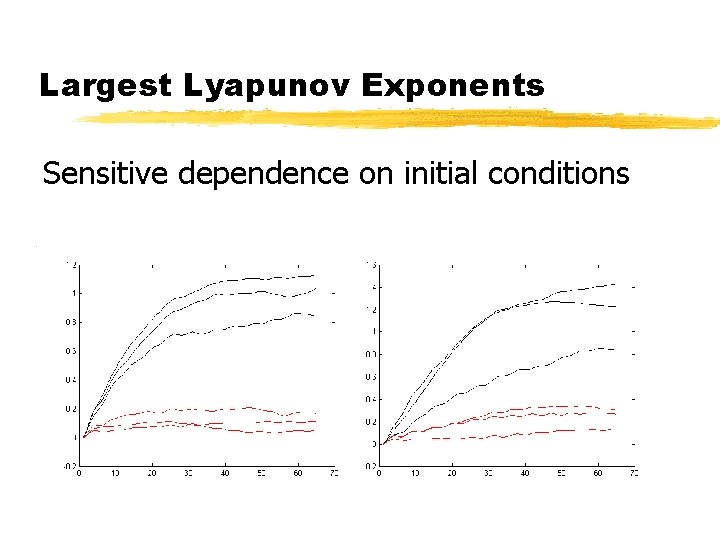
Largest Lyapunov Exponents Sensitive dependence on initial conditions