EEEcon 458 Pareto optimality Benevolent Dictator and Market

EE/Econ 458 Pareto optimality, Benevolent Dictator, and Market Efficiency J. Mc. Calley These slides are your main resource for this topic. 1

Pareto Optimality, Benevolent Dictator, and Market Efficiency The below is what we want to cover in microeconomics. The checkmarks indicate what we have covered so far. • Supply and demand functions√ • Consumers surplus√ • Producers surplus√ • Pareto optimality & benevolent dictator • Market efficiency • Market equilibrium • Competitive equilibrium Today we will discuss Pareto optimality, benevolent dictator, and market efficiency. 2

Pareto Optimality Consider that you are a very nice person that likes to help people, and there are two different families in particular that you desire to assist. You have an extra $1000 to use in assisting these two families. Both families are quite poor. Family 1 consists of an elder husband wife. Family 2 consists of a young husband wife with 4 children. You reason that you can allocate the dollars in many ways, as long as you satisfy x 1+x 2<1000 3

Pareto Optimality x 1+x 2<1000 Now we could choose to allocate $400 to each family. Let’s call this solution A. However, if our objectives are to maximize benefit to the two families, a better solution is to allocate $400 to family 1 and $500 to family 2. This solution, let’s call it solution B, is a better one in that family 2 is better off than they were before and family 1 is no worse off than they were before. You can think of a still better solution: allocate $500 to each family. Call this solution C. Relative to A, both families are better off. Relative to B, only family 1 is better off, but family 2 is no worse off. 4

Pareto Optimality x 1+x 2<1000 Solution A: allocate $400 to each family. Solution B: allocate $400 to family 1 and $500 to family 2 Solution C: allocate $500 to each family Solution C, you reason, is a good solution. Why is it a good solution? It is a good solution because there are no ways you can improve the situation for one family without making the situation worse for the other family. Is solution C the best solution? 5

Pareto Optimality x 1+x 2<1000 What about solution D, where family 1 has $400 and family 2 has $600. This might be better because it gives more to the larger family. But it might not be better because the elderly couple need some expensive medical attention. So it is hard to say…. But one thing you know: solution D is a good solution in that there are, once again, no ways you can improve the situation for one family without making the situation worse for the other family. 6

Pareto Optimality x 1+x 2<1000 This quality of solutions whereby one “objective” cannot be improved without degrading the other “objective” is an important criterion that occurs whenever you have a multiobjective optimization problem, and the objectives conflict. Conflicting objectives exist when improvement in one objective occurs at the expense of the other. Solutions which satisfy the above criterion, i. e. , that one objective cannot be further improved without degrading the other objective, are called Pareto-optimal solutions. And the set of Pareto-Optimal solutions is called the Pareto. Optimal front (or frontier). 7
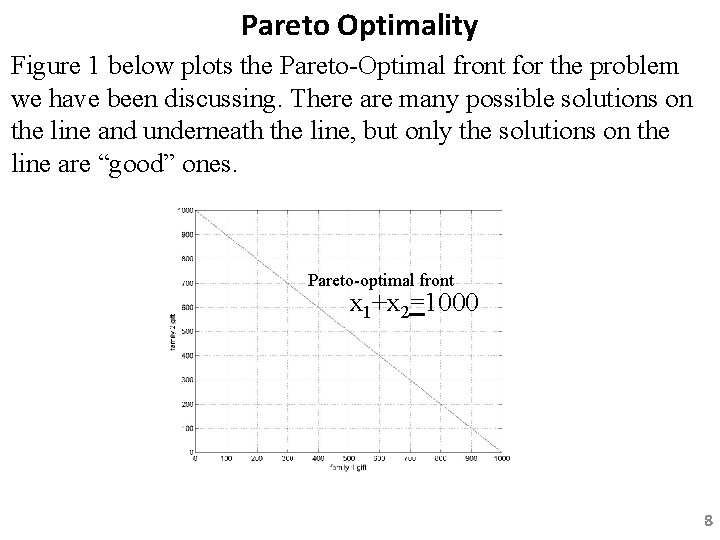
Pareto Optimality Figure 1 below plots the Pareto-Optimal front for the problem we have been discussing. There are many possible solutions on the line and underneath the line, but only the solutions on the line are “good” ones. Pareto-optimal front x 1+x 2=1000 8

Benevolent dictator Adolf Hitler, Germany, 1889 -1945 These were all brutal dictators. Is there such a things as a benevolent dictator? Francisco Franco, Spain 1892 -1975 Benevolent: kind and fair Manuel Noriega, Panama 1934 -2017 Benito Mussolini, Italy 1883 -1945 Idi Amin, Uganda 1925 -2003 Sir Seretse Khama, Botswana, 1921 -1980 He used the country’s resources to grow the economy, and then invested the money gained back into infrastructure, health, and education, which further strengthened the economy, and he achieved free universal education. “the economy”? What’s that? 9

Benevolent dictator Define: 1. Economy: a collection of markets in a defined geographical area. W. Baumol and A. Blinder, “Economics: principles and policy, ” 5 edition, Harcourt Brace College Publishers. James Carville, lead “It’s the economy, stupid” strategist for 1992 th Clinton campaign. 2. Economy: a system of commodity exchange where producers receive money to produce the commodity and consumers pay money to consume the commodity. 2 a. Inside the economy: producers & consumers, the money & commodity they have. 2 b. Outside the economy: entities other than producers & consumers of the commodity, what they have, receive, or give. 10

Benevolent dictator (BD): Someone who has absolute authority over the economy and uses it very well, i. e. , for the benefit of members in the economy. In the energy market, the BD can require any amount of electricity to be demanded and supplied, and so they demand supply an amount of electricity so as to maximize the sum total benefits for all market participants. Who is it in the electricity market who looks like a BD? The market operator! • • • ISONE NYISO PJM MISO SPP ERCOT CAISO IESO AESO 11

Market Efficiency Engineering efficiency An energy conversion system is efficient if it produces a high output for a given input. Market efficiency Loosely, a market system can be said to be efficient if it produces a high benefit to the participants for the cost expended by suppliers and consumers. 12

Market Efficiency Let’s assume that the BD has the following information. • There is a supplier having a cost function C(P) • The consumers have (all of them together) m units of money. • The consumers utility function, expressing their satisfaction (in $) is: (1) Satisfaction ($) associated with the Amount of money available to amount of energy consumed P. consumer after paying to supplier for energy P at price p. The BD also knows that the consumer must respect a constraint: (2) 13

Market Efficiency Thinking as the BD would think, where all money in the economy, and all decisions, are at the disposal of the BD, what should the BD do if s/he wants to maximize overall happiness? The BD does not really care about the shift of money from the consumers to the supplier that occurs via p. P, because this money stays in the economy (and so constraint y=m-p. P is not important to BD). But the expenditures associated with the producer, C(P), leave the economy, and so the BD does care about them. And BD cares about satisfaction obtained from the energy v(P). Therefore, the BD wants to maximize v(P) and the total amount of money in the economy, m-C(P). In other words, the BD wants to solve the following problem: (3 a) 14

Market Efficiency (3 a) But m is just a constant, therefore (3 a) is identical to (3 b) Taking first order conditions: (4) Equation (4) expresses the condition on consumption and production that the BD needs to satisfy in order to maximize the happiness for the people… 15

Market Efficiency (4) Equation (4) expresses the condition on consumption and production that the BD needs to satisfy in order to maximize the happiness for the people, and that is: The optimal level of consumption and supply, P, is obtained when the marginal utility v’(P) is equal to the marginal cost C’(P), that is, when the willingness to pay for an additional unit of energy equals the cost of producing one additional unit. Before we think further, I want to make an observation of what we are maximizing…let’s call our objective F. What is F? (3 b) 16

Market Efficiency (5) Add and subtract p. P to F: (6) Move the –p. P+p. P term to the left: (7) Group terms: (8) Recall: equal, with v(0)=0 (9) equal, with C(0)=0 (10) 17

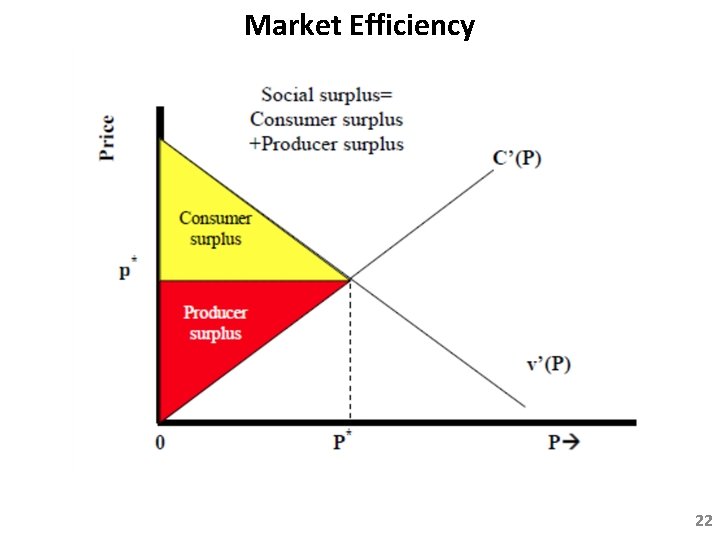
Market Efficiency Then (11) (12) (13) Definition: The sum of consumer surplus and producer surplus is called the social surplus. It is a measure of the total benefit seen by an economy and it is what the BD wants to maximize. The BD achieves the goal, i. e. , the social surplus is maximized, when (4) is met, i. e. , when the marginal utility v’(P) is equal to the marginal cost C’(P). (4) 18

BD wants to maximize satisfaction and total money in the economy. This is equivalent to maximizing total surplus, which we call social surplus. Market Efficiency (3 b) (13) (4) • If willingness to pay for an additional unit of energy is higher than its cost of production, BD can increase the social surplus by producing one more unit. • If willingness to pay for an additional unit of energy is lower than its cost of production, then we could increase social surplus by producing one unit less. • It is only when the willingness to pay for an additional unit of energy equals the cost of producing one additional unit can we be maximizing the social surplus. 19

Market Efficiency This is illustrated on the next slide. 20
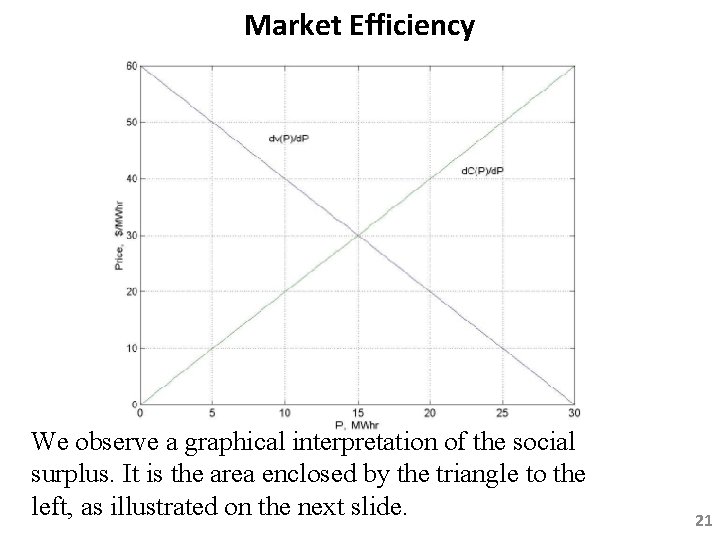
Market Efficiency We observe a graphical interpretation of the social surplus. It is the area enclosed by the triangle to the left, as illustrated on the next slide. 21
Market Efficiency 22

Market Efficiency 23
- Slides: 23