EEE 436 DIGITAL COMMUNICATION Coding En Mohd Nazri

EEE 436 DIGITAL COMMUNICATION Coding En. Mohd Nazri Mahmud MPhil (Cambridge, UK) BEng (Essex, UK) nazriee@eng. usm. my Room 2. 14 EE 436 Lecture Notes 1

Error Detection and Correction Syndrome Decoding involves parity-check information derived from the code’s coefficient matrix, P. Associated with any systematic linear (n, k) block code is a (n-k)-byn matrix, H called the parity-check matrix. H is defined as H = [In-k PT] Where PT is the transpose of the coefficient matrix, P and is an (n-k)-by-k matrix. In-k is the (n-k)-by-(n-k) identity matrix. For error detection purposes, the parity check matrix, H has the following property EE 436 Lecture Notes c. HT = (0 0 …. . 0) (ie Null matrix) 2

Syndrome Decoding c. HT = (0 0 …. . 0) (ie Null matrix) Since c=m. G, therefore m. G. HT = (0 0 …. 0) This property is satisfied only when c is correctly received. Errors are indicated by the presence of non-zero elements in the matrix. Let r denotes the 1 -by-n received vector that results from sending the code vector c over a noisy channel. When there is an error, the decoding operation will give a syndrome vector, s whose elements contain at least 1 non-zero element. EE 436 Lecture Notes 3

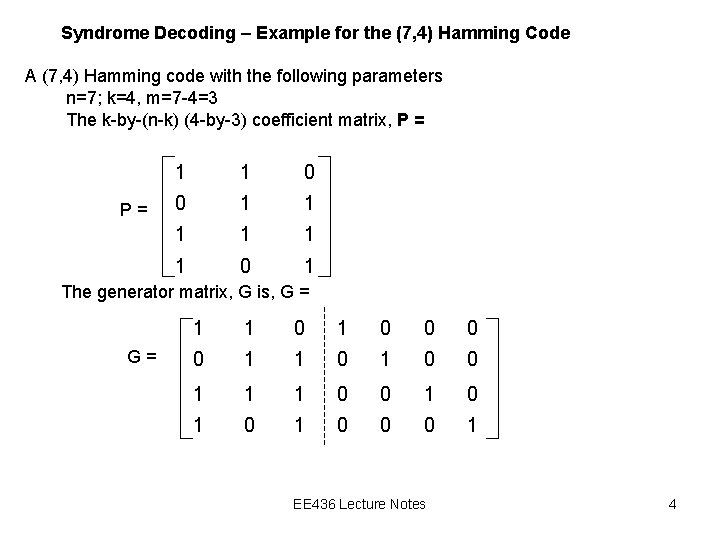
Syndrome Decoding – Example for the (7, 4) Hamming Code A (7, 4) Hamming code with the following parameters n=7; k=4, m=7 -4=3 The k-by-(n-k) (4 -by-3) coefficient matrix, P = P= 1 1 0 0 1 1 1 0 1 The generator matrix, G is, G = G= 1 1 0 0 0 0 1 1 1 0 0 1 0 1 0 0 0 1 EE 436 Lecture Notes 4

Syndrome Decoding –Example for (7, 4) Hamming Code Associated with the (7, 4) Hamming Code is a 3 -by-7 matrix, H called the parity-check matrix. H is defined as H = [In-k PT] 1 0 0 1 0 1 1 1 0 0 0 1 1 1 When a codeword is correctly received, the c. HT will result in a null matrix, otherwise it will result in a syndrome vector, s. EE 436 Lecture Notes 5

Syndrome Decoding –Example for (7, 4) Hamming Code Example: The received code vector is [1110010], check whether this is a correct codeword c. HT = [1110010] 1 0 0 0 1 1 1 0 0 1 EE 436 Lecture Notes 6

Syndrome Decoding –Example for (7, 4) Hamming Code Example: The received code vector is [1100010], check whether this is a correct codeword c. HT = [1100010] 1 0 0 0 1 1 1 0 0 1 = [0 0 1] – this is called the error syndrome EE 436 Lecture Notes 7

Error pattern is an error vector E whose nonzero element mark the position of the transmission errors in the received codeword We can work out all syndromes and find the corresponding error patterns and store them in a look up table for decoding purposes For example the (7, 4) Hamming code EE 436 Lecture Notes 8

Error detection & correction The error pattern, E is essentially the modulo-2 sum of the correct code vector and the erroneous received code vector. For example , c = 1110010 and r=1100010 (ie error in the 3 rd bit) c + r =E 1110010 + 1100010 = 0010000 This error pattern corresponds to a syndrome vector in the look up table, 001 Recall that the syndrome vector, s = r. HT s = (c + E)HT = c. HT + EHT = EHT EE 436 Lecture Notes 9

Error detection and correction Therefore, the decoding procedure involves working out the syndrome for the received code vector and look up for the corresponding error pattern. Then, modulo-2 sum the error pattern, E and the received vector, r , so that c = r + E, and the correct codeword can be recovered. EE 436 Lecture Notes 10

Error detection and correction Example For message word 0010, the correctly encoded codeword is c = 1110010. Due to channel noise, the received code vector is r = [1100010]. Show the decoder recover the correct codeword. 1) The decoder uses r and the HT to find the error syndrome, s S=r. HT = 001 2) Using the resulting syndrome, refer the look up table for the corresponding assumed error vector, E. S=001 corresponds to assumed error vector, E = 0010000 3) Then ex-OR E and r to recover the correct codeword E+r = 0010000 + 1100010 = 1110010 EE 436 Lecture Notes 11

Error detection and correction Exercise i) ii) For message word 0110, the correctly encoded codeword is c = 1000110. Due to channel noise, the received code vector is r = [1100110]. Show the decoder recover the correct codeword. For message word 0110, the correctly encoded codeword is c = 1000110. Due to channel noise, the received code vector is r = [1100100]. Show the decoder performs its decoding operation. What is your observation and explain it. EE 436 Lecture Notes 12

BCH Codes • A class of cyclic codes discovered in 1959 by Hocquenghem and in 1960 by Bose and Ray-Chaudhuri. • Include both binary and multilevel codes • Identified in the form of (n, k) BCH code for example (15, 7) BCH code • A t-error Binary BCH codes consist of binary sequences of length n= 2 m – 1 ; m indicates the corresponding Galois Field • Specified by its generator polynomial, g • The generator polynomial is specified in terms of its roots from the Galois Field, GF(2 m) EE 436 Lecture Notes 13

BCH Codes • To work out the corresponding generator polynomial for example (15, 7) BCH code • First, we need to find m; since n=2 m -1, therefore, for n=15; m = 4 • Then we need to find the primitive polynomial for m=4 from a specified reference table • Then, based on the primitive polynomial, construct the elements of GF(24) • Then find the minimal polynomials of the elements of GF(24) from a specified reference table • Then based on these minimal polynomials , we can work out the generator polynomial. EE 436 Lecture Notes 14

Binary BCH Codes • For our example, (15, 7) BCH code consider a Galois Field with m=4 GF(24) • A polynomial p(X) over GF(24) of degree 4 that is primitive is taken from the following Table of primitive polynomials EE 436 Lecture Notes 15

Binary BCH Codes • • Then, based on the primitive polynomial, 1 + X 4 construct the elements of GF(24) Let alpha (ά) be a primitive element in GF(2 m) Set p(ά)=1+ ά+ ά 4 = 0 , then ά 4 = 1+ ά Using this relation, we can construct GF(24) elements as below EE 436 Lecture Notes 16

Binary BCH Codes Then find the minimal polynomials of the elements of GF(24) from a specified reference table EE 436 Lecture Notes 17

Binary BCH Codes Then the generator polynomial of a t-error correcting BCH code of length 2 m – 1 is given by g(x) = LCM { ǿ 1(X), ǿ 2(X) , …. . , ǿ 2 t (X) } Since every even power of ά in the elements sequence has the same minimal polynomial as some preceding odd power of ά in the elements sequence g(x) = LCM { ǿ 1(X), ǿ 3(X) , …. . , ǿ 2 t-1 (X) } EE 436 Lecture Notes 18

Binary BCH Codes generator polynomial – Example A(15, 7) BCH code (ie n=15) m=2 m-1; m=4 Therefore , refer to Galois Field with m=4 GF(24) A polynomial p(X) over GF(24) of degree 4 that is primitive is taken the table p(X)= 1 + X 4 Then, based on the primitive polynomial, 1 + X 4 construct the elements of GF(24) Then find the minimal polynomials of the elements of GF(24) from the table Then the generator polynomial of a t-error correcting BCH code of length 2 m – 1 is given by g(x) = LCM { ǿ 1(X), ǿ 3(X) , …. . , ǿ 2 t-1 (X) } EE 436 Lecture Notes 19

Binary BCH Codes generator polynomial – Example Then the generator polynomial of a t-error correcting BCH code of length 2 m – 1 is given by g(x) = LCM { ǿ 1(X), ǿ 3(X) , …. . , ǿ 2 t-1 (X) } For 2 -error correcting; t=2 Therefore, g(x) = LCM { ǿ 1(X), ǿ 3(X)} ǿ 1(X) = 1 + X 4 and ǿ 3(X)= 1 + X 2 + X 3 + X 4 g(x) = ǿ 1(X). ǿ 3(X) = 1 + X 4 + X 6 + X 7 + X 8 Exercise : Try out for 3 -error correcting BCH code of the same length EE 436 Lecture Notes 20

Binary BCH Codes generator polynomials – Example EE 436 Lecture Notes 21

Non-Binary or M-ary BCH Codes • Unlike binary these codes are multilevel codes • Operates on multiple bits rather than individual bits • The general (n, k) encoder encodes k m-bit symbols into blocks consisting of n=2 m-1 symbols of total m(2 m-1) bits • Thus the encoding expands a block of k symbols to n symbols by adding n-k redundant symbols • An example of non-binary BCH code is the Reed -Solomon Code EE 436 Lecture Notes 22

RS Codes • A t-error-correcting RS code has the following parameters – – Block length n= 2 m-1 Message size k symbols Parity-check size n-k=2 t symbols Minimum distance = 2 t + 1 • Example RS(7, 4) with m=3 bits EE 436 Lecture Notes 23