EEE 436 DIGITAL COMMUNICATION Coding En Mohd Nazri

EEE 436 DIGITAL COMMUNICATION Coding En. Mohd Nazri Mahmud MPhil (Cambridge, UK) BEng (Essex, UK) nazriee@eng. usm. my Room 2. 14 EE 436 Lecture Notes 1

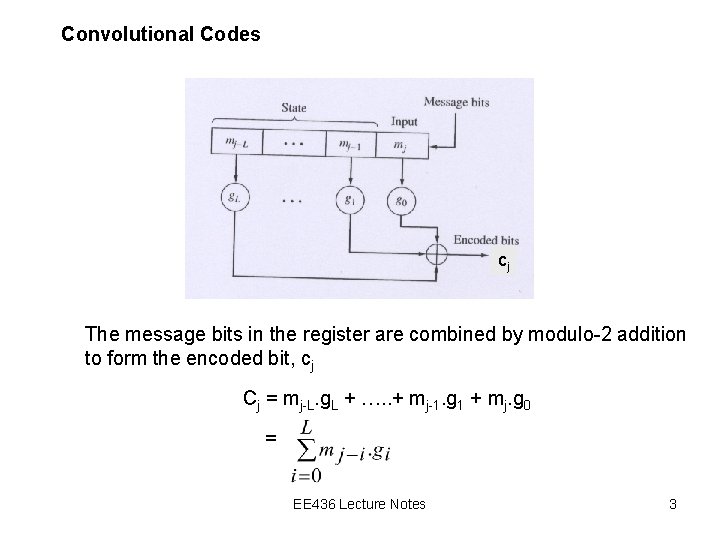
Convolutional Codes Unlike block codes that operate on block-by-block basis, the convolutional codes are based on message bits that come in serially rather than in blocks. The structure of a generic convolutional encoder can be written in a compact form of (n, k, L) ; n= no of streams, or no of modulo-2 adder; k=number of group of shift register; L=number of state of the shift register The encoder takes an L-bit message sequence to produce a coded output sequence of length n(L+M) bits, where n=no of stream of the encoded bits, M=no of bits of message sequence The encoder is implemented by a tapped shift register with L+1 stages. EE 436 Lecture Notes 2

Convolutional Codes cj The message bits in the register are combined by modulo-2 addition to form the encoded bit, cj Cj = mj-L. g. L + …. . + mj-1. g 1 + mj. g 0 = EE 436 Lecture Notes 3

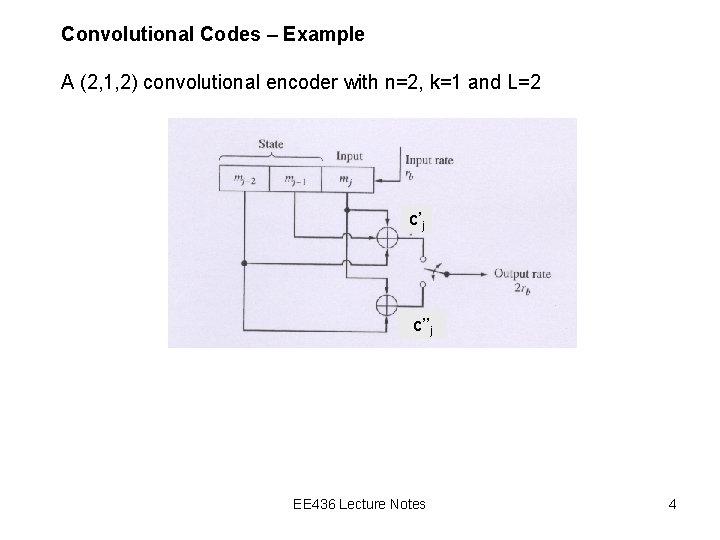
Convolutional Codes – Example A (2, 1, 2) convolutional encoder with n=2, k=1 and L=2 c’j c’’j EE 436 Lecture Notes 4

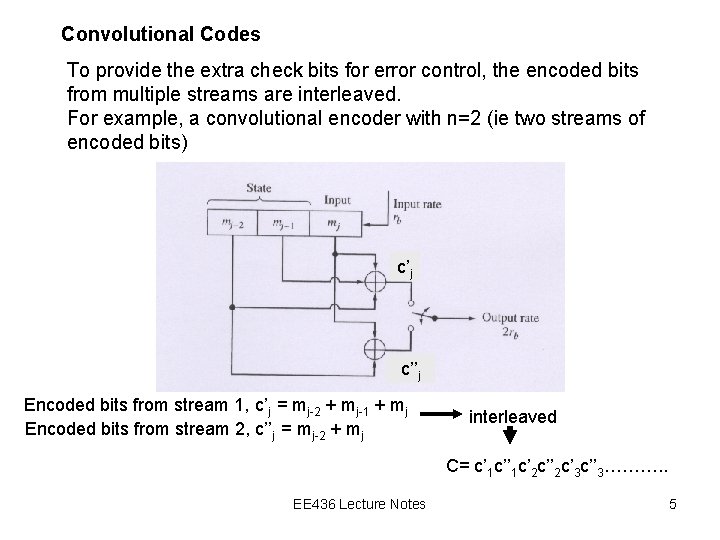
Convolutional Codes To provide the extra check bits for error control, the encoded bits from multiple streams are interleaved. For example, a convolutional encoder with n=2 (ie two streams of encoded bits) c’j c’’j Encoded bits from stream 1, c’j = mj-2 + mj-1 + mj Encoded bits from stream 2, c’’j = mj-2 + mj interleaved C= c’ 1 c’ 2 c’’ 2 c’ 3 c’’ 3………. . EE 436 Lecture Notes 5

Convolutional Codes Each stream may be characterised in terms of its impulse response ( the response of that stream to a symbol 1 with zero initial condition). Every stream is also characterised in terms of a generator polynomial, which is the unit-delay transform of the impulse response Let the following generator sequence denotes the impulse response of the i-th path The generator polynomial of the i-th path is given by Where D denotes the unit-delay variable EE 436 Lecture Notes 6

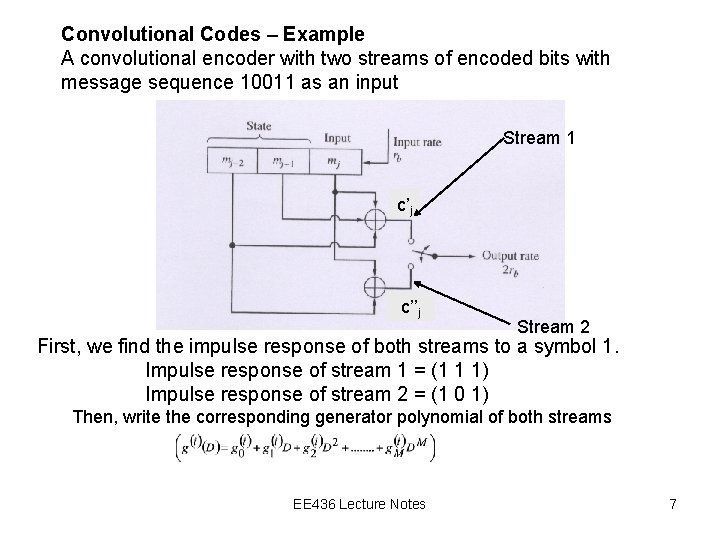
Convolutional Codes – Example A convolutional encoder with two streams of encoded bits with message sequence 10011 as an input Stream 1 c’j c’’j Stream 2 First, we find the impulse response of both streams to a symbol 1. Impulse response of stream 1 = (1 1 1) Impulse response of stream 2 = (1 0 1) Then, write the corresponding generator polynomial of both streams EE 436 Lecture Notes 7

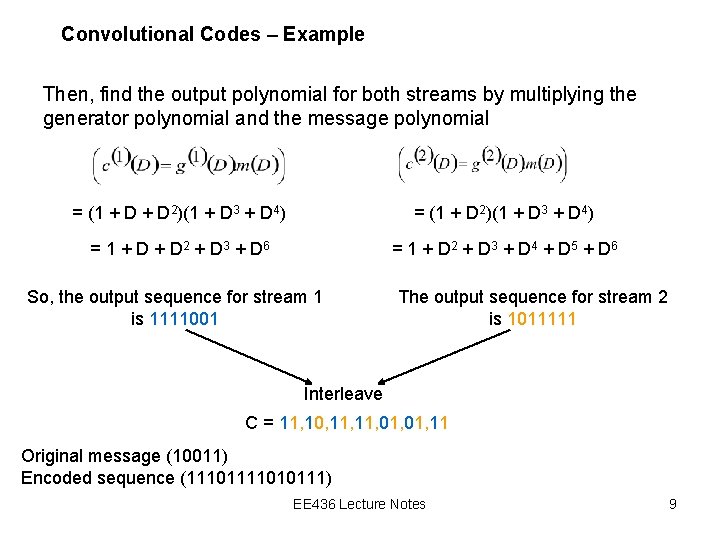
Convolutional Codes – Example First, we find the impulse response of both streams to a symbol 1. Impulse response of stream 1 = (1 1 1) Impulse response of stream 2 = (1 0 1) Then, write the corresponding generator polynomials of both streams Then, write the message polynomial for input message (10011) Then, find the output polynomial for both streams by multiplying the generator polynomial and the message polynomial EE 436 Lecture Notes 8

Convolutional Codes – Example Then, find the output polynomial for both streams by multiplying the generator polynomial and the message polynomial = (1 + D 2)(1 + D 3 + D 4) = 1 + D 2 + D 3 + D 6 = 1 + D 2 + D 3 + D 4 + D 5 + D 6 So, the output sequence for stream 1 is 1111001 The output sequence for stream 2 is 1011111 Interleave C = 11, 10, 11, 01, 11 Original message (10011) Encoded sequence (111010111) EE 436 Lecture Notes 9

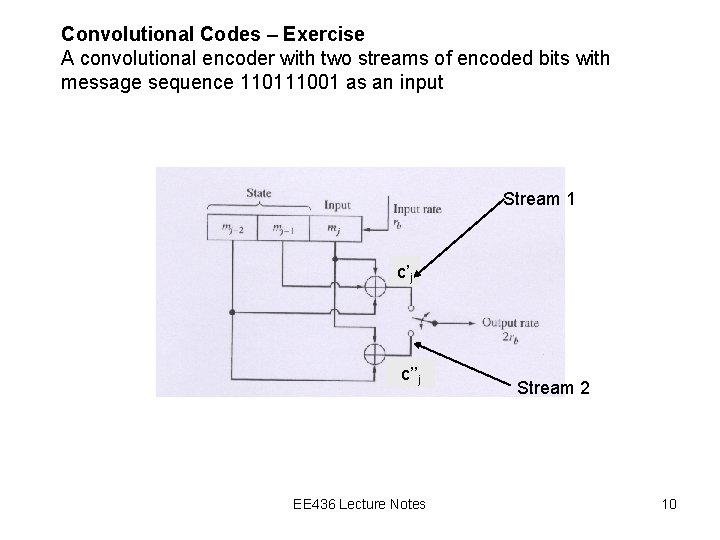
Convolutional Codes – Exercise A convolutional encoder with two streams of encoded bits with message sequence 110111001 as an input Stream 1 c’j c’’j EE 436 Lecture Notes Stream 2 10

Convolutional Codes – Exercise First, we find the impulse response of both streams to a symbol 1. Impulse response of stream 1 = (1 1 1) Impulse response of stream 2 = (1 0 1) Then, write the corresponding generator polynomials of both streams Then, write the message polynomial for input message (110111001) Then, find the output polynomial for both streams by multiplying the generator polynomial and the message polynomial EE 436 Lecture Notes 11

Convolutional Codes – Exercise Then, find the output polynomial for both streams by multiplying the generator polynomial and the message polynomial = 1 + D 5 + D 7 + D 8 + D 9 + D 10 = 1 + D +D 2 + D 4 + D 6 + D 7 + D 8 + D 10 So, the output sequence for stream 1 is 10000101111 The output sequence for stream 2 is 11101011101 Interleave C = 11 01 01 00 01 11 11 10 11 Original message (110111001) Encoded sequence (11 01 01 00 01 11 11 10 11 ) EE 436 Lecture Notes 12

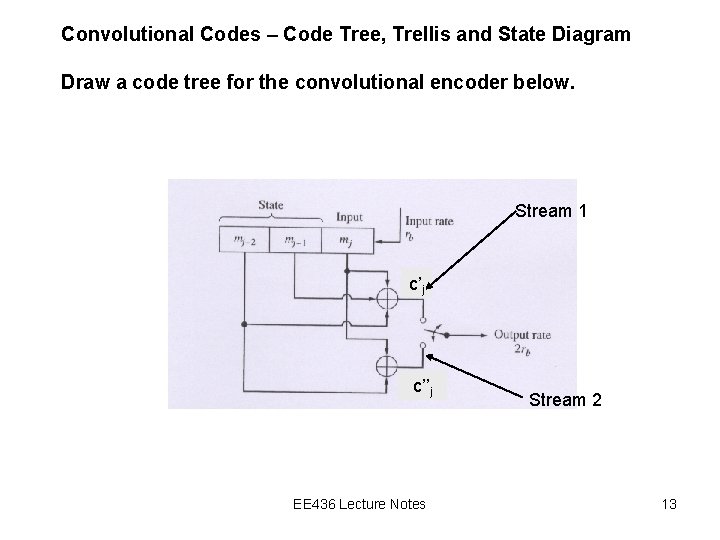
Convolutional Codes – Code Tree, Trellis and State Diagram Draw a code tree for the convolutional encoder below. Stream 1 c’j c’’j EE 436 Lecture Notes Stream 2 13

Code Tree EE 436 Lecture Notes 14

Trellis EE 436 Lecture Notes 15

State Diagram EE 436 Lecture Notes 16

Maximum Likelihood Decoding of a Convolutional Code Let m denotes a message vector c denotes the corresponding code vector r the received code vector (which may differ from c due to channel noise) Given the received vector r, the decoder is required to make an estimate m^ of the message vector Since there is a one-to-one correspondence between the message vector m and the code vector c, therefore m^ = m only if c^ = c , otherwise a decoding error is committed The decoding rule is said to be optimum when the probability of decoding error is minimised EE 436 Lecture Notes 17

Maximum Likelihood Decoding of a Convolutional Code Let say both the transmitted code vector c and the received vector r represent binary sequence of length N. These two sequences may differ from each other in some locations because of errors due to channel noise. Let ci and ri denote the ith element of c and r respectively We then have The decoding rule is said to be optimum when the probability of decoding error is minimised EE 436 Lecture Notes 18

Correspondingly, the log-likelihood is The probability of decoding error is minimised if the log-likelihood function is maximized (the estimate c^ is chosen to maximise the function) Let the transition probability be defined as If If EE 436 Lecture Notes 19

Suppose also that the received vector r differs from the transmitted code vector c in exactly d positions (where d is the Hamming distance between vectors r and c) We may rewrite the log-likelihood function as EE 436 Lecture Notes 20

In general, the probability of error occurring is low enough for us to assume p < ½ And also that Nlog(1 -p) is constant for all c. The function is maximised when d is minimised. (ie the smallest Hamming distance) “ Choose the estimate c^ that minimise the Hamming distance between The received vector r and the transmitted vector c. ” The maximum likelihood decoder is reduced to a minimum distance decoder. The received vector r is compared with each possible transmitted code vector c and the particular one “closest” to r is chosen as the correct transmitted code vector. EE 436 Lecture Notes 21

The Viterbi Algorithm The equivalence between maximum likelihood decoding and minimum distance decoding implies that we may decode a convolutional code by choosing a path in the code tree whose coded sequence differs from the received sequence in the fewest number of places Since a code tree is equivalent to a trellis, we may limit our choice to the possible Paths in the trellis representation of the code. Viterbi algorithm operates by computing a metric or discrepancy for every possible Path in the trellis The metric for a particular path is defined as the Hamming distance between the Coded sequence represented by that path and the received sequence. For each state in the trellis, the algorithm compares the two paths entering the node And the path with the lower metric is retained. The retained paths are called survivors. The sequence along the path with the smallest metric is the maximum likelihood Choice and represent the transmitted sequence EE 436 Lecture Notes 22

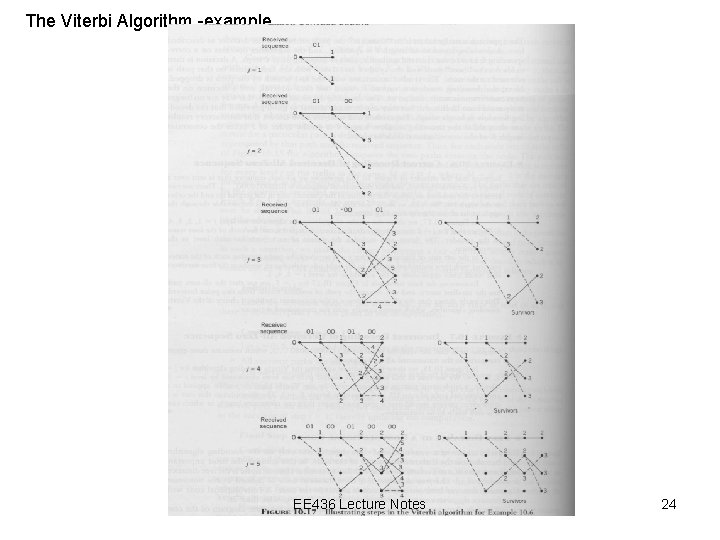
The Viterbi Algorithm -example In the circuit beliow, suppose that the encoder generates an all-zero sequence and that the received sequence is (010000…) in which the are two errors due to channel noise: one in second bit and the other in the sixth bit. We can show that this double-error pattern is correctable using the Viterbi algorithm. Stream 1 c’j c’’j EE 436 Lecture Notes Stream 2 23

The Viterbi Algorithm -example EE 436 Lecture Notes 24

The Viterbi Algorithm -exercise Using the same circuit, suppose that the received sequence is 110111. Using the Viterbi algorithm, what is the corresponding encoded sequence transmitted by the receiver? What is the original message bit? EE 436 Lecture Notes 25