EEE 431 Computational Methods in Electrodynamics Lecture 16

EEE 431 Computational Methods in Electrodynamics Lecture 16 By Dr. Rasime Uyguroglu Rasime. uyguroglu@emu. edu. tr 1

Electrostatic Charge Distribution and The Method of Moments l l Consider again the finite straight wire at a constant potential which was discussed in Lecture 15. From statics we know that a linear electric charge distribution will create an electric potential, V(r): 2

Electrostatic Charge Distribution and The Method of Moments l l This equation may be used to find potentials due to the known line charge densities. However, for most of the practical cases the charge distributions are unknown even when the potential on the source is given. 3

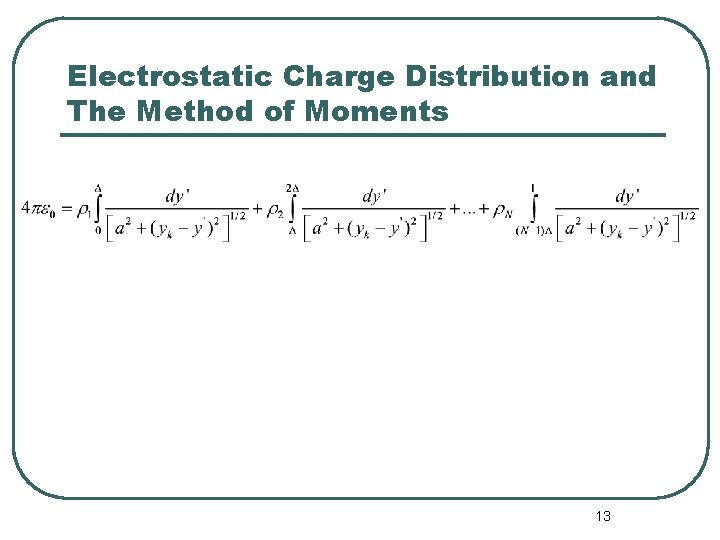
Electrostatic Charge Distribution and The Method of Moments l l The wire has a length of along the y direction. It’s radius is , and it is connected to a battery of 1 Volts. Choosing the observation point along the wire axis: 4

Electrostatic Charge Distribution and The Method of Moments l Where: 5

Electrostatic Charge Distribution and The Method of Moments l l l The equation above is an integral equation to be solved for the unknown Such problems are called inverse problems. The solution of the integral equation may be obtained numerically by reducing it to a series of algebraic equations that may be solved by conventional matrix techniques. 6

Electrostatic Charge Distribution and The Method of Moments l Approximate the unknown charge distribution by an expansion of N known terms with constant, but unknown, coefficients, that is: 7

Electrostatic Charge Distribution and The Method of Moments l Thus the integral equation can be written as: 8

Electrostatic Charge Distribution and The Method of Moments l The above equation is a nonsingular integral, its integration can be changed to summation: 9

Electrostatic Charge Distribution and The Method of Moments l l l The functions in the expansion are chosen to model accurately the unknown quantity and minimize the computation. These functions are called basis (or expansion) functions. In this solution pulse function (subdomain piecewise constant) will be used. 10

Electrostatic Charge Distribution and The Method of Moments l The wire is divided into N segments having lengths of: y 11

Electrostatic Charge Distribution and The Method of Moments l These functions are defined to be of constant value over one segment and zero elsewhere. Or: 12

Electrostatic Charge Distribution and The Method of Moments 13

Electrostatic Charge Distribution and The Method of Moments l The matrix form: 14

Electrostatic Charge Distribution and The Method of Moments l l Or: Where: (T: transpose) 15

Electrostatic Charge Distribution and The Method of Moments l l l Where: (NXN) matrix to be generated. (NX 1) excitation column vector (known). (NX 1) unknown response column vector to be found. Then the solution is: 16

Electrostatic Charge Distribution and The Method of Moments l l The integrals involved may be solved by using appropriate approximations. But this may not be possible for complicated problems. Efficient numerical integration computer subroutines are available. 17

Electrostatic Charge Distribution and The Method of Moments l l l Summary: The solution of the integral equation for the charge distribution on a wire has been discussed. The unknown charge was approximated with some basis functions, dividing the wire into segments and then sequentially enforcing at the center of each segment to form a set of linear equations. 18

Method of Moments l l Electromagnetic problems usually involve solution of linear partial differential equations or integral equations. The general form is: 19

Method of Moments l Two electrostatic examples are: Poisson’s equation, differential equation: l Coulomb’s Law: l 20

Method of Moments/ Green’ Function l In general: l Where the kernel G(r, r’) is the Green’s function. 21

Method of Moments/ Green’ Function l l Green’s functions offer a systematic way of converting a Differential Equation (DE) to an Integral Equation (IE). A Green’s function is the solution of the DE corresponding to an impulsive (unit) excitation 22

Method of Moments/ Green’ Function l Green’s Function provides a method of dealing with the source term g. (in ) 23

Method of Moments/ Green’ Function l l To solve problems of type The method of moments begins by approximating the unknown function by a linear combination of unknown functions in the form: 24

Method of Moments/ Green’ Function l l The functions are called basis or expansion functions. They are selected such that the appropriate values of the parameters on the right side of this equation is a reasonably accurate approximation to the left side. 25

Method of Moments/ Green’ Function l l l Basis Functions: One very important step in any solution is the choice of the basis functions. 1)Entire domain functions (span the entire domain) 2)Subdomain Functions (each one of is zero except in a subdomain. 26

Method of Moments/ Green’ Function l The subdomain approach involves subdivision of the structure into N non overlapping segments. The simplest one is the pulse. Piecewise continuous: 27

Inner Product l Inner (dot or scalar) Product of two functions w, g: l * indicates the complex conjugate. 28

Weighting (Testing Functions) l l l Here w’s are the weighting functions and s is the surface of the structure being analyzed (will be discussed). Note that the functions w and g can be vectors. This technique is known as the method of moments. ( Mo. M) 29

Moment Methods (Method of Moments, Mo. M) l l l The procedure for applying Mo. M to solve the equation above usually involves four steps: 1)Derivation of the appropriate integral equation (IE). 2)Conversion (discretization) of IE into a matrix equation using basis (or expansions) functions and weighting functions. 30

Moment Methods (Method of Moments, Mo. M) l l 3)Evaluation of the matrix elements. 4)Solving the matrix equation and obtaining the parameters of interest. The basic tools for step 2 will be discussed. Mo. M will be applied to IEs rather than PDEs. 31