EEE 241 Fundamentals of Electromagnetics Introductory Concepts Vector

EEE 241: Fundamentals of Electromagnetics Introductory Concepts, Vector Fields and Coordinate Systems Instructor: Dragica Vasileska

Outline • • Class Description Introductory Concepts Vector Fields Coordinate Systems

Class Description Prerequisites by Topic: – University physics – Complex numbers – Partial differentiation – Multiple Integrals – Vector Analysis – Fourier Series

Class Description • Prerequisites: EEE 202; MAT 267, 274 (or 275), MAT 272; PHY 131, 132 • Computer Usage: Students are assumed to be versed in the use Math. CAD or MATLAB to perform scientific computing such as numerical calculations, plotting of functions and performing integrations. Students will develop and visualize solutions to moderately complicated field problems using these tools. • Textbook: Cheng, Field and Wave Electromagnetics.

Class Description • Grading: Midterm #1 Midterm #2 Final Homework 25% 25%

Class Description

Why Study Electromagnetics?

Examples of Electromagnetic Applications

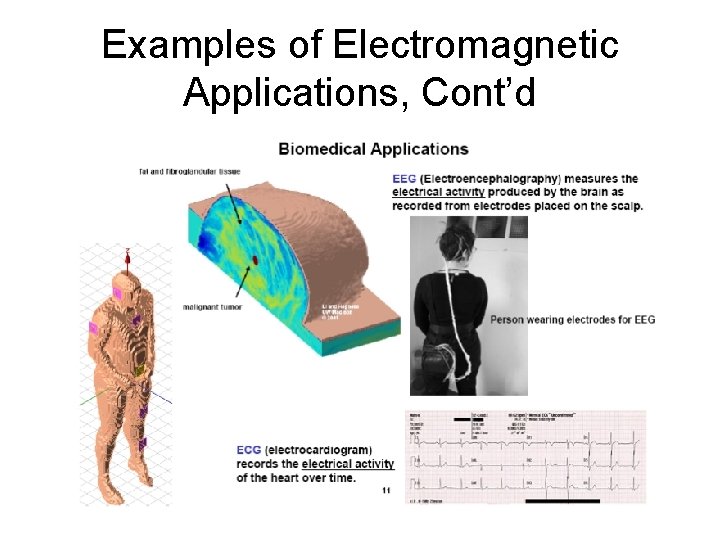
Examples of Electromagnetic Applications, Cont’d

Examples of Electromagnetic Applications, Cont’d

Examples of Electromagnetic Applications, Cont’d

Examples of Electromagnetic Applications, Cont’d

Research Areas of Electromagnetics • • Antenas Microwaves Computational Electromagnetics Electromagnetic Scattering Electromagnetic Propagation Radars Optics etc …

Why is Electromagnetics Difficult?

What is Electromagnetics?

What is a charge q?

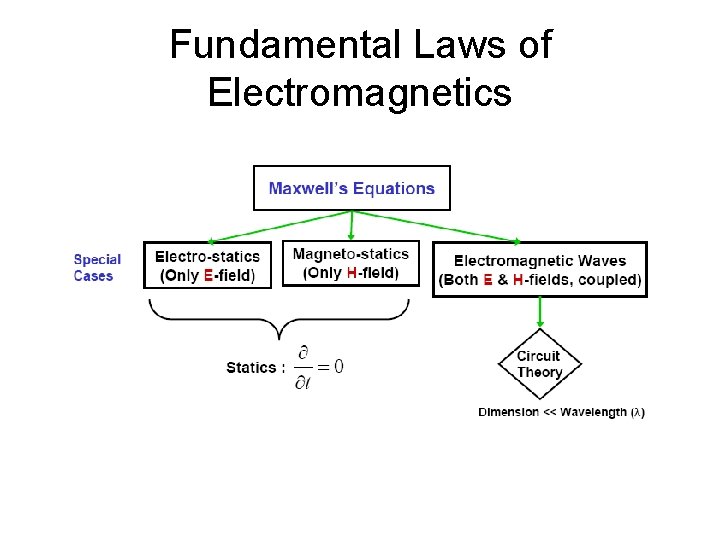
Fundamental Laws of Electromagnetics

Steps in Studying Electromagnetics

SI (International System) of Units

Units Derived From the Fundamental Units

Fundamental Electromagnetic Field Quantities

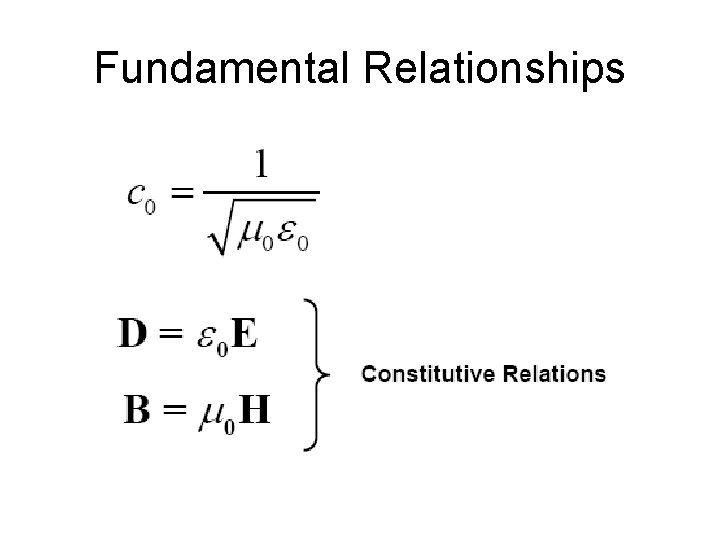
Three Universal Constants

Fundamental Relationships

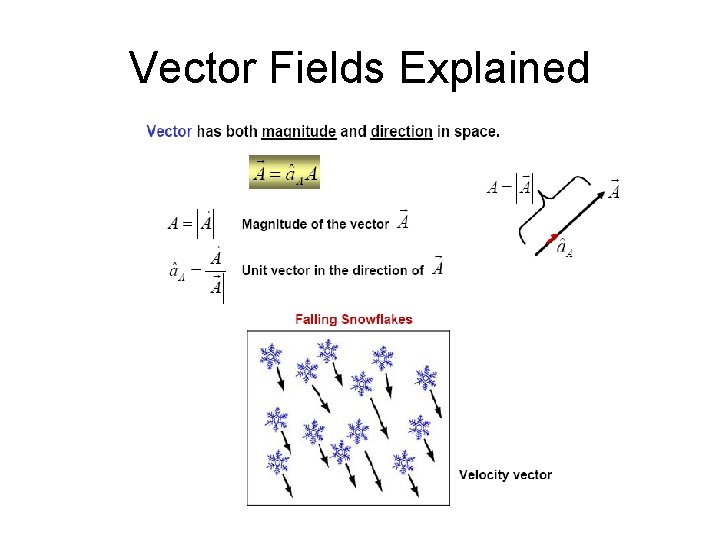
Scalar and Vector Fields • A scalar field is a function that gives us a single value of some variable for every point in space. • Examples: voltage, current, energy, temperature • A vector is a quantity which has both a magnitude and a direction in space. • Examples: velocity, momentum, acceleration and force

Example of a Scalar Field

Scalar Fields e. g. Temperature: Every location has associated value (number with units) 26

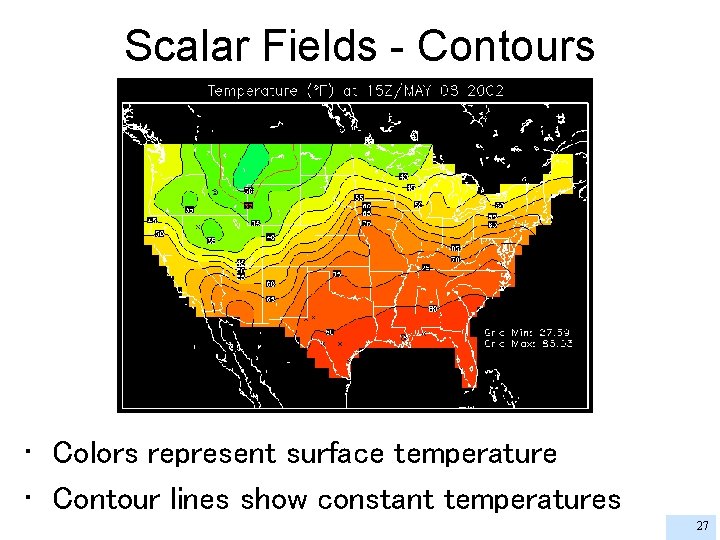
Scalar Fields - Contours • Colors represent surface temperature • Contour lines show constant temperatures 27

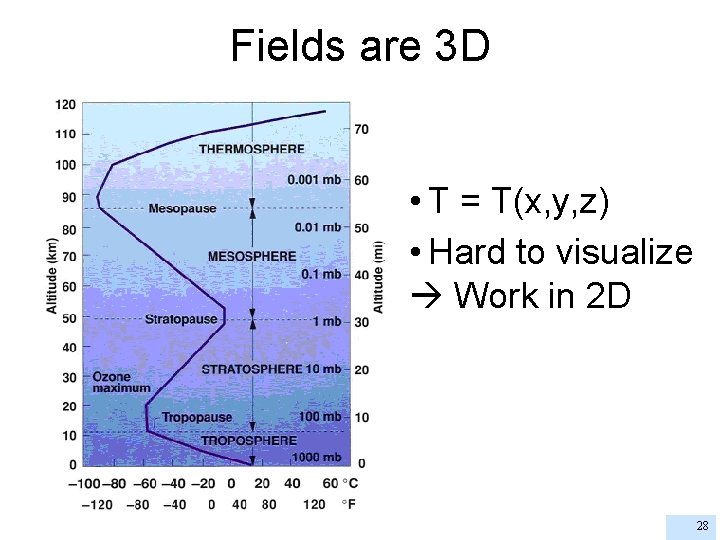
Fields are 3 D • T = T(x, y, z) • Hard to visualize Work in 2 D 28

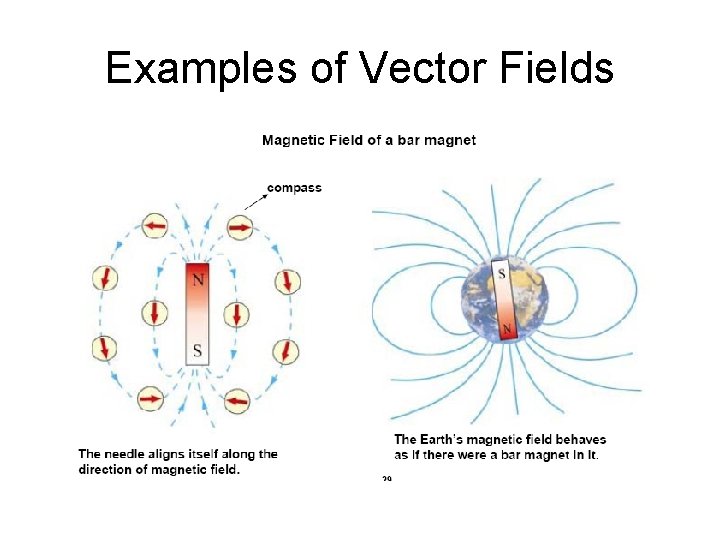
Vector Fields Vector (magnitude, direction) at every point in space Example: Velocity vector field - jet stream 29

Vector Fields Explained

Examples of Vector Fields

Examples of Vector Fields

Examples of Vector Fields

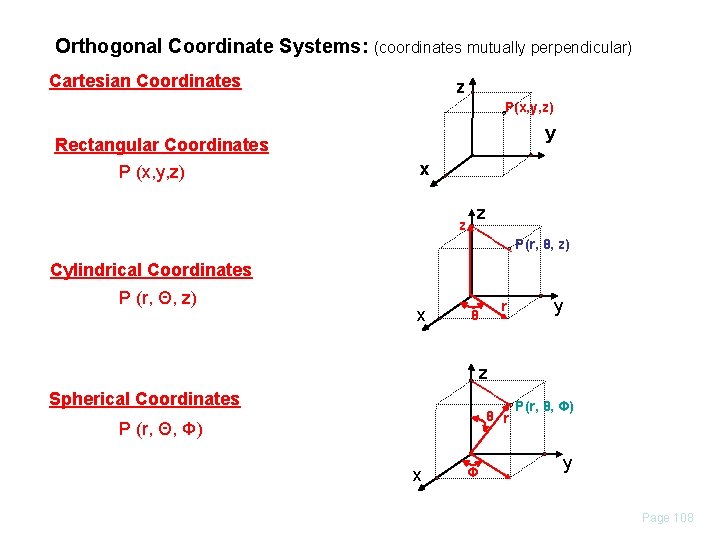
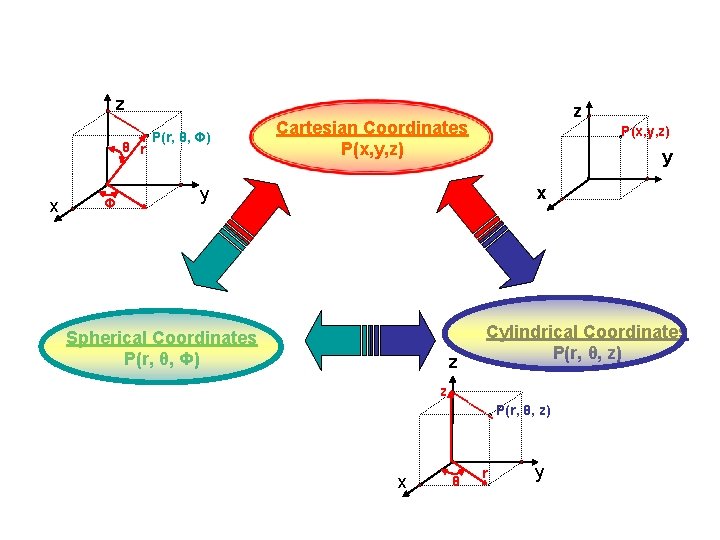
VECTOR REPRESENTATION 3 PRIMARY COORDINATE SYSTEMS: • RECTANGULAR • CYLINDRICAL • SPHERICAL Choice is based on symmetry of problem Examples: Sheets - RECTANGULAR Wires/Cables - CYLINDRICAL Spheres - SPHERICAL

Orthogonal Coordinate Systems: (coordinates mutually perpendicular) Cartesian Coordinates z P(x, y, z) Rectangular Coordinates P (x, y, z) y x z z P(r, θ, z) Cylindrical Coordinates P (r, Θ, z) x r θ y z Spherical Coordinates θ r P (r, Θ, Φ) x Φ P(r, θ, Φ) y Page 108

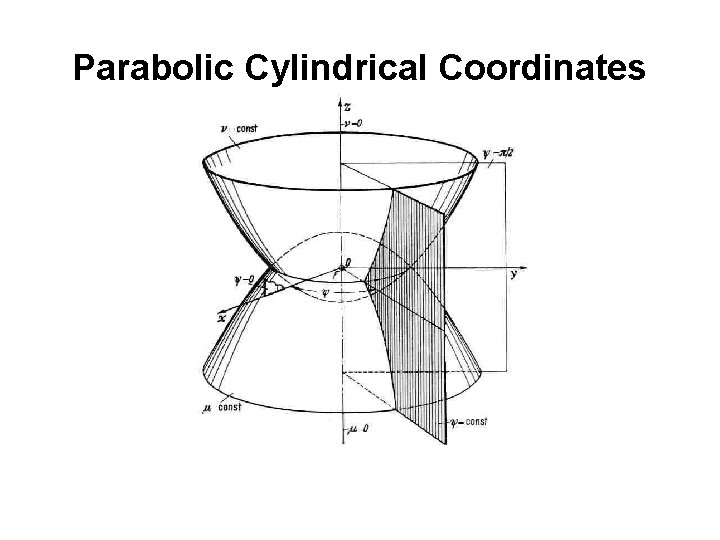
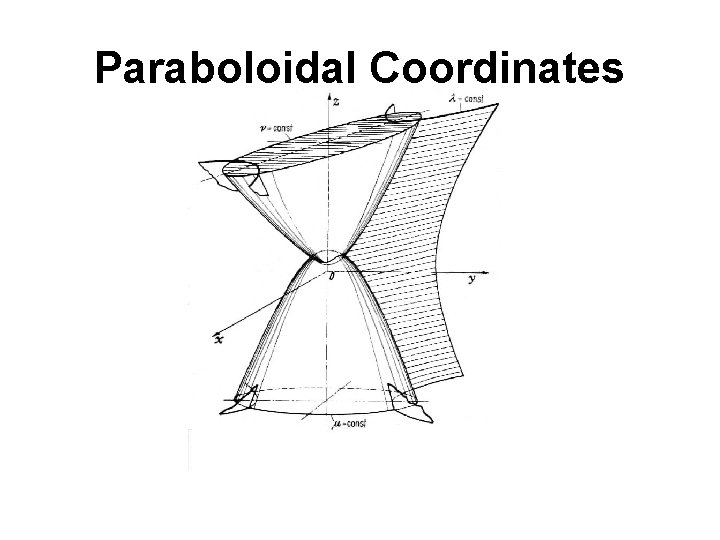
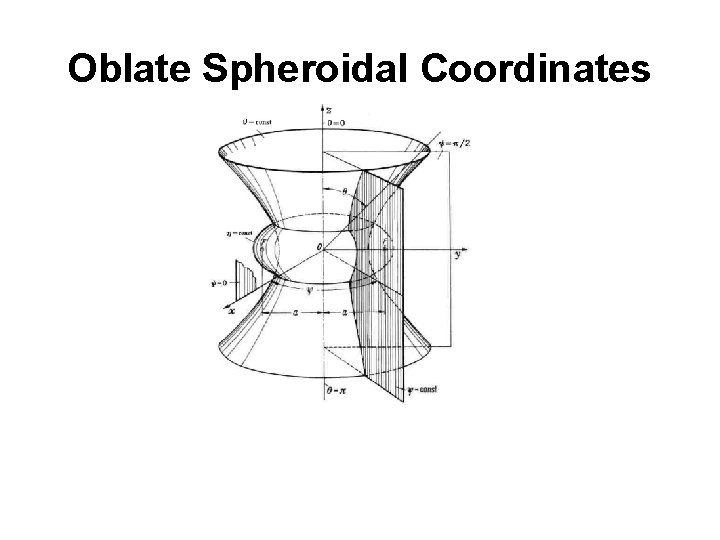
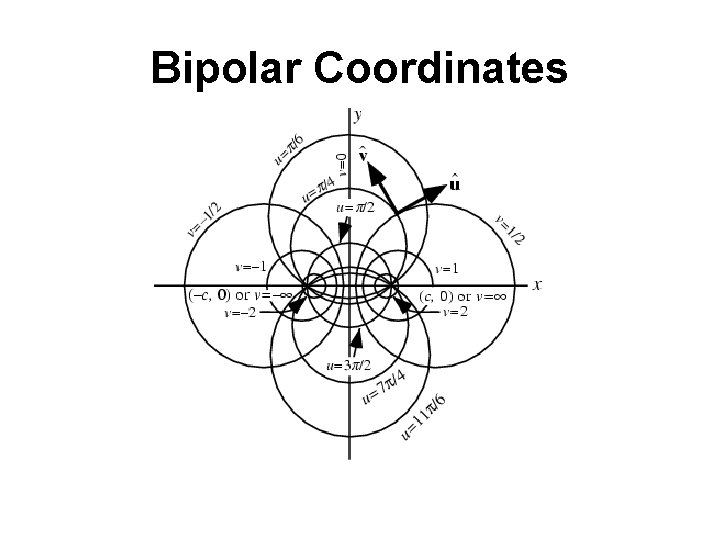
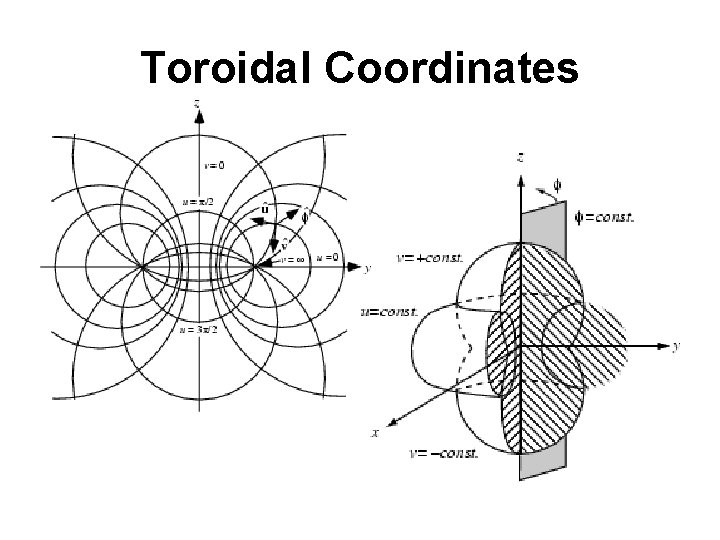
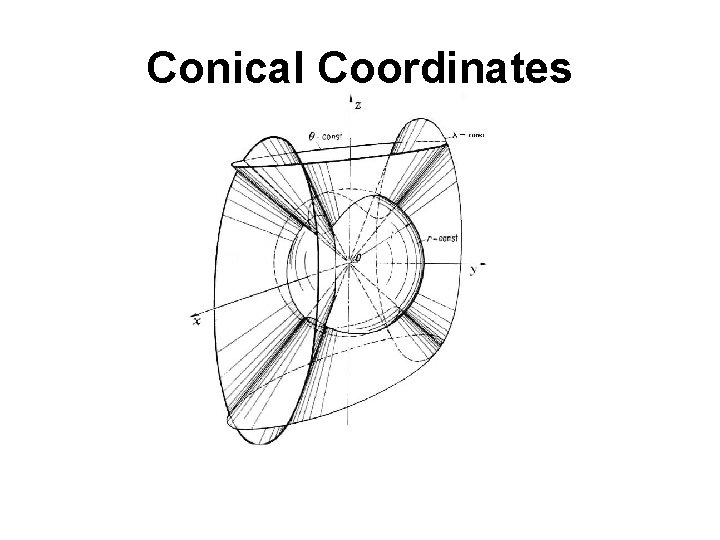
-Parabolic Cylindrical Coordinates (u, v, z) -Paraboloidal Coordinates (u, v, Φ) -Elliptic Cylindrical Coordinates (u, v, z) -Prolate Spheroidal Coordinates (ξ, η, φ) -Oblate Spheroidal Coordinates (ξ, η, φ) -Bipolar Coordinates (u, v, z) -Toroidal Coordinates (u, v, Φ) -Conical Coordinates (λ, μ, ν) -Confocal Ellipsoidal Coordinate (λ, μ, ν) -Confocal Paraboloidal Coordinate (λ, μ, ν)

Parabolic Cylindrical Coordinates

Paraboloidal Coordinates

Elliptic Cylindrical Coordinates

Prolate Spheroidal Coordinates

Oblate Spheroidal Coordinates

Bipolar Coordinates

Toroidal Coordinates

Conical Coordinates

Confocal Ellipsoidal Coordinate

Confocal Paraboloidal Coordinate

z θ r x Φ P(r, θ, Φ) z Cartesian Coordinates P(x, y, z) y x y Spherical Coordinates P(r, θ, Φ) z Cylindrical Coordinates P(r, θ, z) z P(r, θ, z) x θ r y

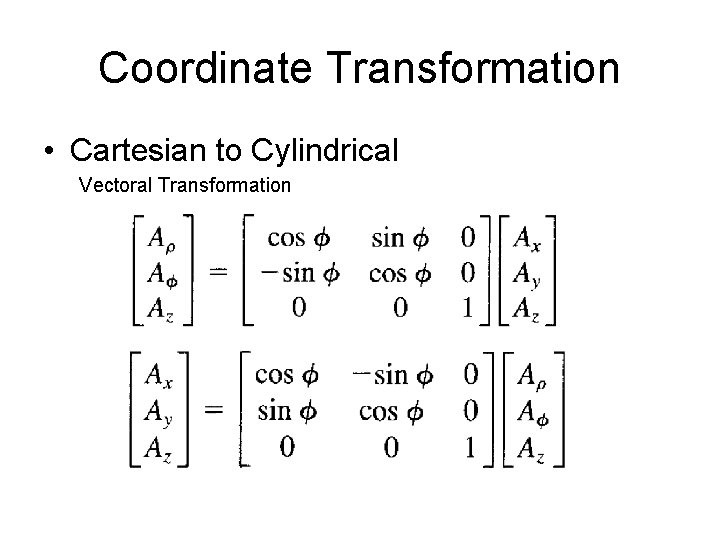
Coordinate Transformation • Cartesian to Cylindrical (x, y, z) to (r, θ, Φ) to (x, y, z)

Coordinate Transformation • Cartesian to Cylindrical Vectoral Transformation

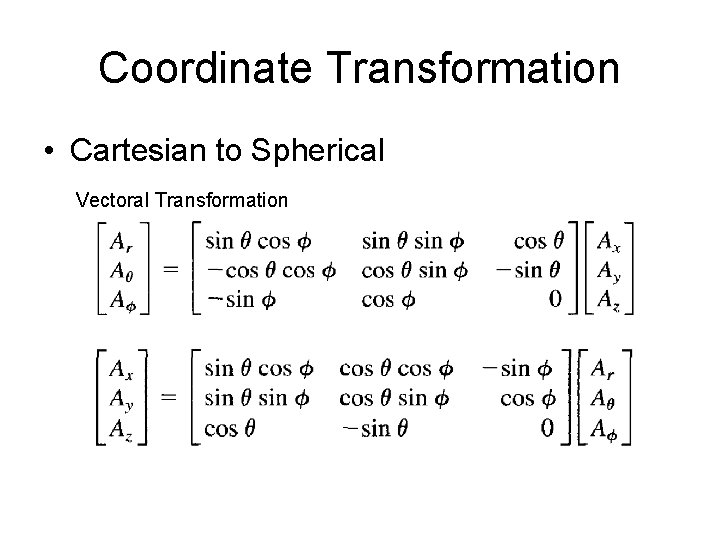
Coordinate Transformation • Cartesian to Spherical (x, y, z) to (r, θ, Φ) to (x, y, z)

Coordinate Transformation • Cartesian to Spherical Vectoral Transformation

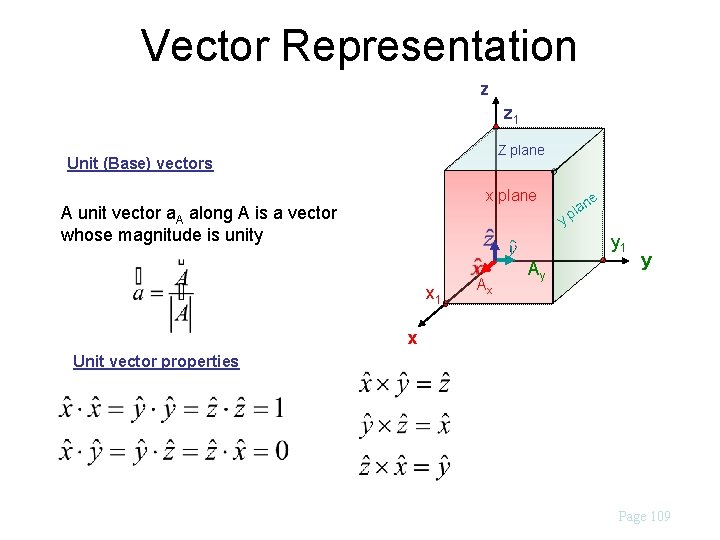
Vector Representation z z 1 Z plane Unit (Base) vectors x plane A unit vector a. A along A is a vector whose magnitude is unity ne la yp y 1 x 1 Ax Ay y x Unit vector properties Page 109

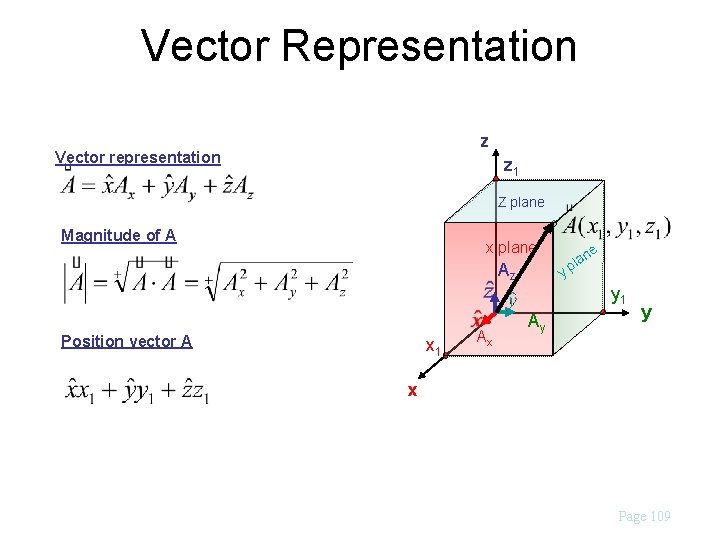
Vector Representation z Vector representation z 1 Z plane Magnitude of A x plane Az ne la yp y 1 Position vector A x 1 Ax Ay y x Page 109

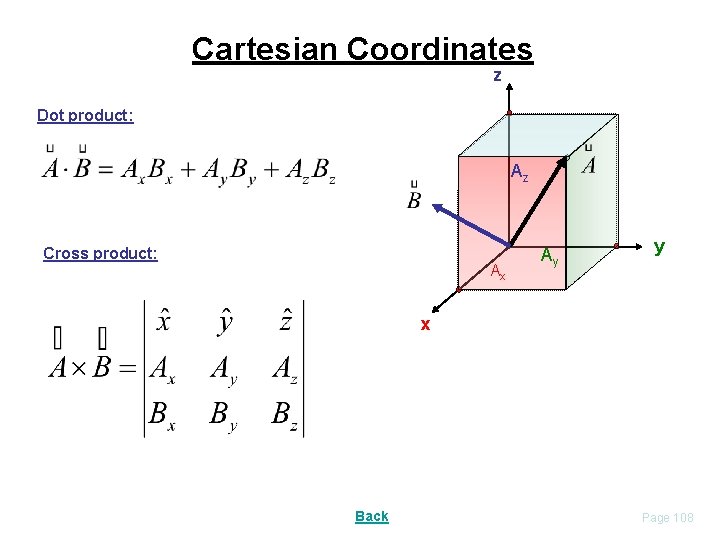
Cartesian Coordinates z Dot product: Az Cross product: Ax Ay y x Back Page 108

Multiplication of vectors • Two different interactions (what’s the difference? ) – Scalar or dot product : • the calculation giving the work done by a force during a displacement • work and hence energy are scalar quantities which arise from the multiplication of two vectors • if A·B = 0 – The vector A is zero – The vector B is zero – = 90° A B

– Vector or cross product : • n is the unit vector along the normal to the plane containing A and B and its positive direction is determined as the right-hand screw rule • the magnitude of the vector product of A and B is equal to the area of the parallelogram formed by A and B • if there is a force F acting at a point P with position vector r relative to an origin O, the moment of a force F about O is defined by : • if A x B = 0 – The vector A is zero – The vector B is zero – = 0° A B

Commutative law : Distribution law : Associative law :

Unit vector relationships • It is frequently useful to resolve vectors into components along the axial directions in terms of the unit vectors i, j, and k.

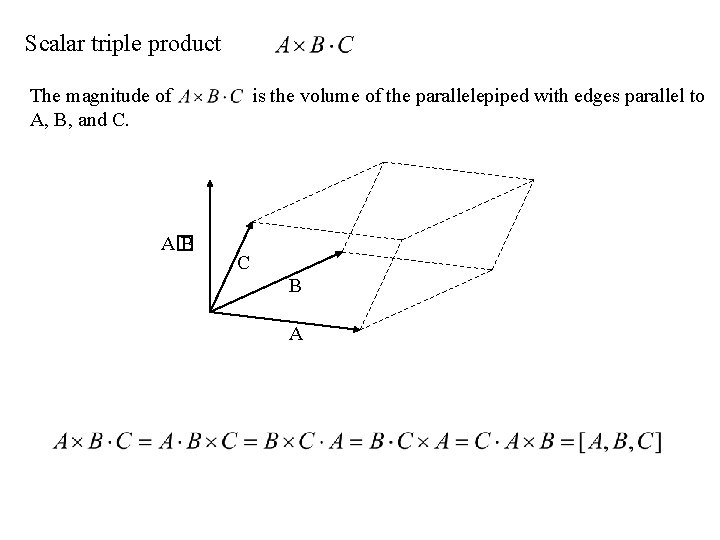
Scalar triple product The magnitude of A, B, and C. A� B is the volume of the parallelepiped with edges parallel to C B A

Vector triple product The vector is perpendicular to the plane of A and B. When the further vector product with C is taken, the resulting vector must be perpendicular to and hence in the plane of A and B : where m and n are scalar constants to be determined. Since this equation is valid for any vectors A, B, and C Let A = i, B = C = j: A� B C B A

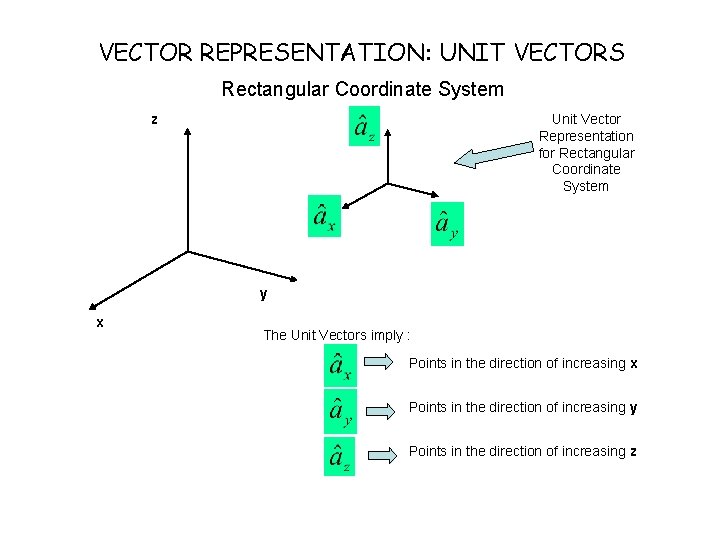
VECTOR REPRESENTATION: UNIT VECTORS Rectangular Coordinate System z Unit Vector Representation for Rectangular Coordinate System y x The Unit Vectors imply : Points in the direction of increasing x Points in the direction of increasing y Points in the direction of increasing z

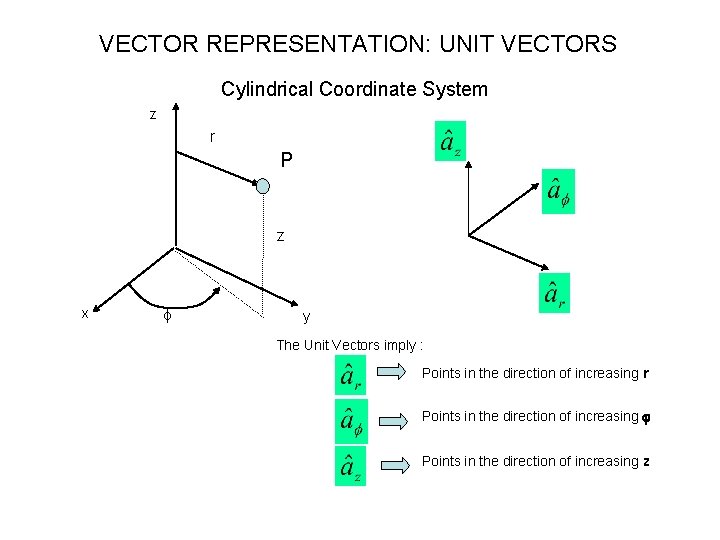
VECTOR REPRESENTATION: UNIT VECTORS Cylindrical Coordinate System z r P z x f y The Unit Vectors imply : Points in the direction of increasing r Points in the direction of increasing j Points in the direction of increasing z

Cylindrical Coordinates ( ρ, Φ, z) ρ radial distance in x-y plane Φ azimuth angle measured from the positive x-axis A 1 Z Vector representation Base Vectors Magnitude of A Base vector properties Position vector A Back Pages 109 -112

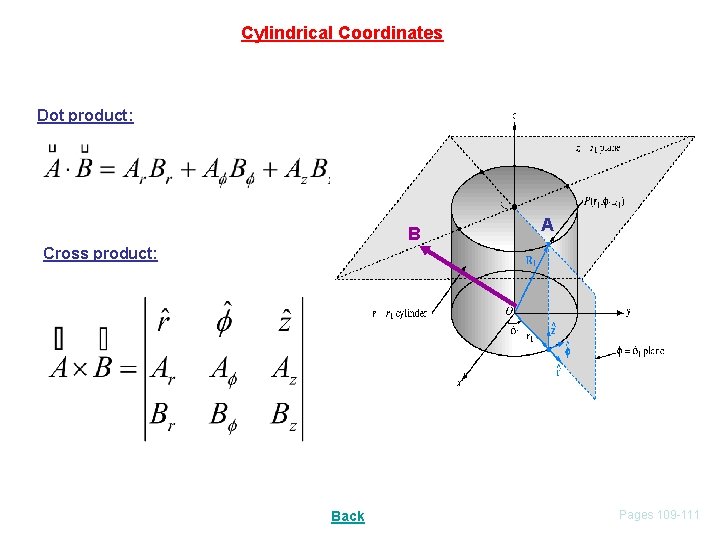
Cylindrical Coordinates Dot product: B A Cross product: Back Pages 109 -111

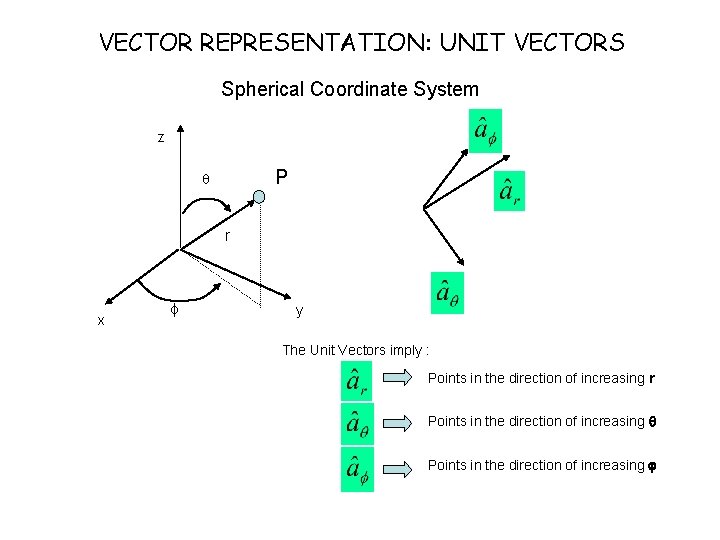
VECTOR REPRESENTATION: UNIT VECTORS Spherical Coordinate System z P r x f y The Unit Vectors imply : Points in the direction of increasing r Points in the direction of increasing q Points in the direction of increasing j

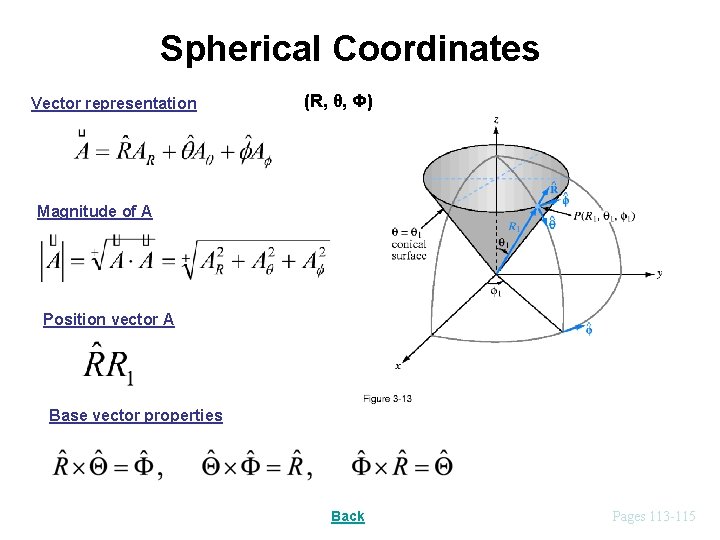
Spherical Coordinates Vector representation (R, θ, Φ) Magnitude of A Position vector A Base vector properties Back Pages 113 -115

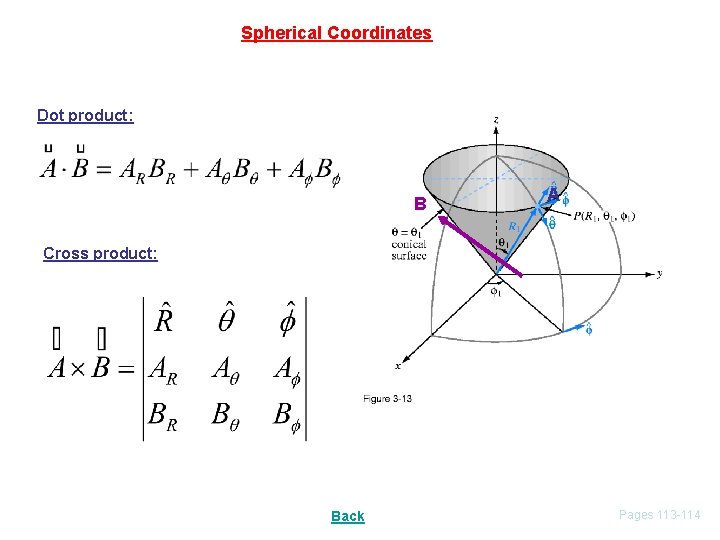
Spherical Coordinates Dot product: B A Cross product: Back Pages 113 -114

VECTOR REPRESENTATION: UNIT VECTORS Summary RECTANGULAR Coordinate Systems CYLINDRICAL Coordinate Systems SPHERICAL Coordinate Systems NOTE THE ORDER! r, f, z r, , f Note: We do not emphasize transformations between coordinate systems

METRIC COEFFICIENTS 1. Rectangular Coordinates: Unit is in “meters” When you move a small amount in x-direction, the distance is dx In a similar fashion, you generate dy and dz

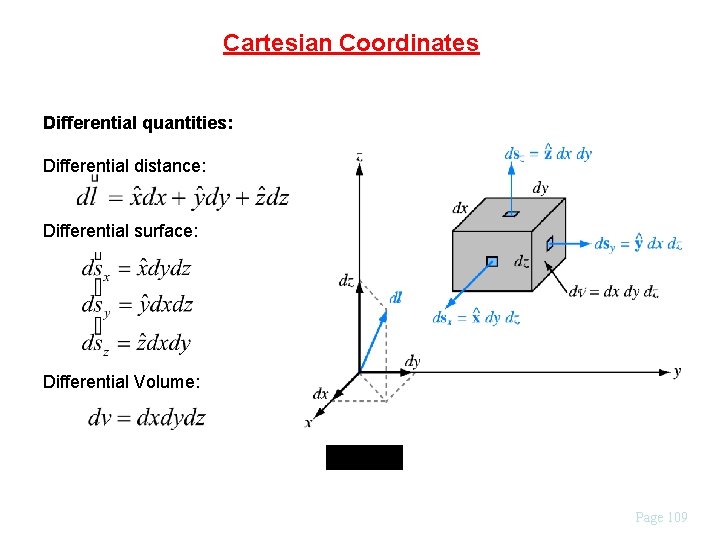
Cartesian Coordinates Differential quantities: Differential distance: Differential surface: Differential Volume: Page 109

Cylindrical Coordinates: y Distance = r df df r x Differential Distances: ( dr, rdf, dz )

Cylindrical Coordinates: Differential Distances: ( dρ, rdf, dz ) Differential Surfaces: Differential Volume:

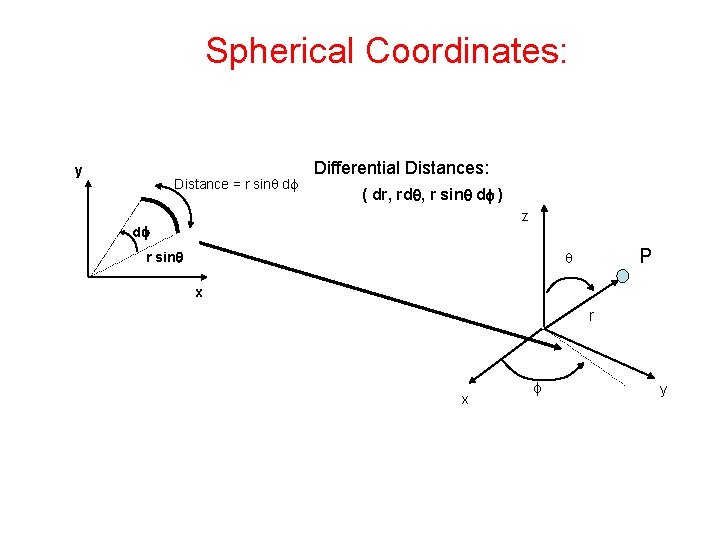
Spherical Coordinates: y Distance = r sin df Differential Distances: ( dr, rdq, r sinq df ) z df P r sinq x r x f y

Spherical Coordinates Differential quantities: Length: Area: Volume: Back Pages 113 -115

METRIC COEFFICIENTS Representation of differential length dl in coordinate systems: rectangular cylindrical spherical

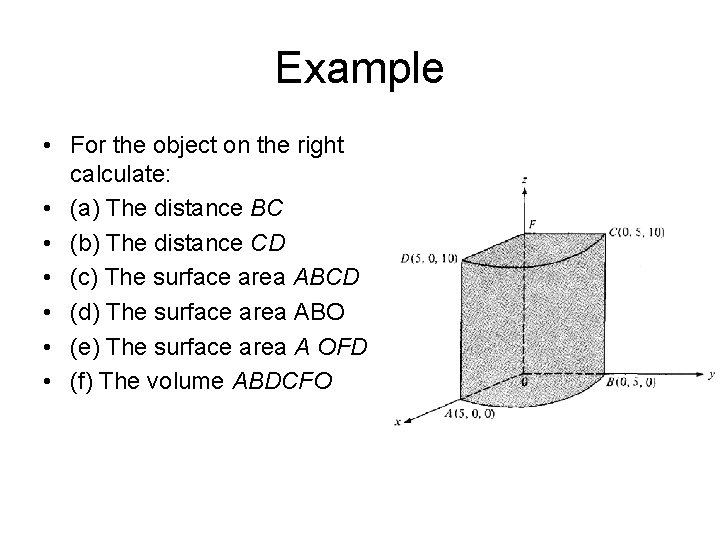
Example • For the object on the right calculate: • (a) The distance BC • (b) The distance CD • (c) The surface area ABCD • (d) The surface area ABO • (e) The surface area A OFD • (f) The volume ABDCFO

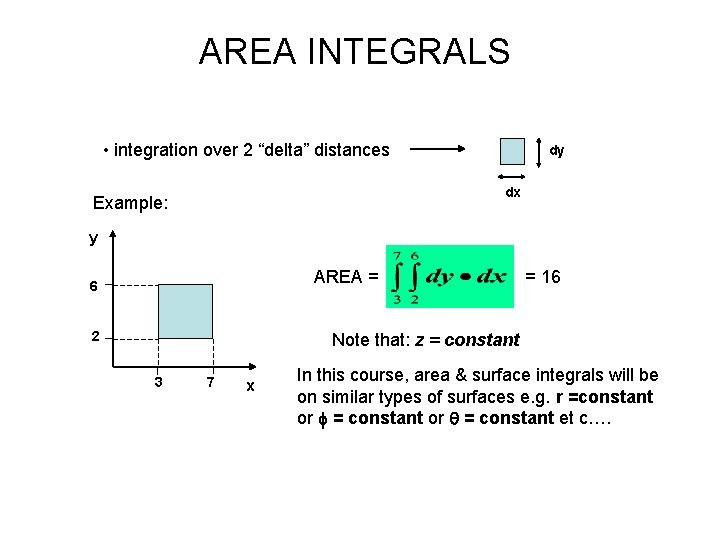
AREA INTEGRALS • integration over 2 “delta” distances dy dx Example: y AREA = 6 2 = 16 Note that: z = constant 3 7 x In this course, area & surface integrals will be on similar types of surfaces e. g. r =constant or f = constant or q = constant et c….

SURFACE NORMAL Representation of differential surface element: Vector is NORMAL to surface

DIFFERENTIALS FOR INTEGRALS Example of Line differentials or or Example of Surface differentials or Example of Volume differentials

Cartesian to Cylindrical Transformation Back Page 115