EEE 161 Applied Electromagnetics Dr Milica Markovic 11252020

EEE 161 Applied Electromagnetics Dr. Milica Markovic 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 1

Chapter 1 VECTORS 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 2

Scalars and Vectors • Scalars quantities are defined by magnitude only: – Temperature 75 deg. F – Mass 75 kg • Vectors are defined by magnitude and direction: – Wind speed 75 m/h in NW direction 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 3

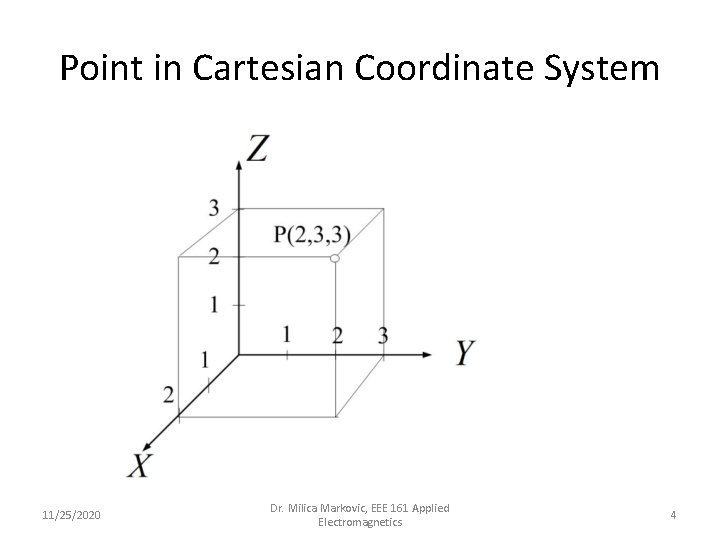
Point in Cartesian Coordinate System 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 4

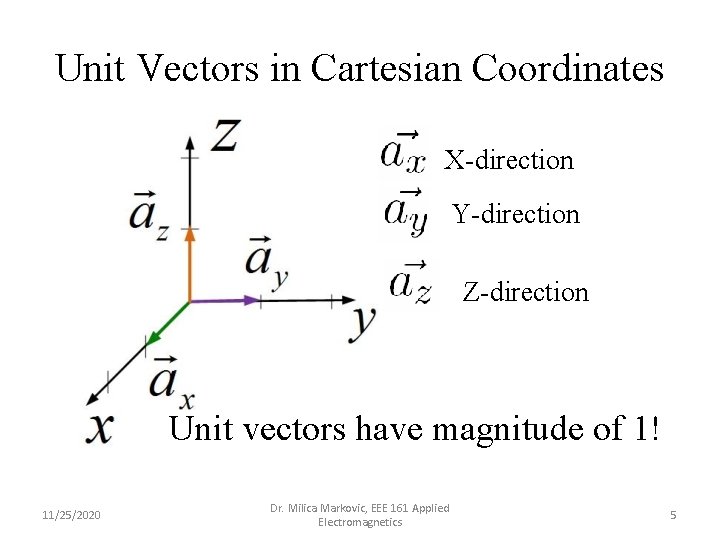
Unit Vectors in Cartesian Coordinates X-direction Y-direction Z-direction Unit vectors have magnitude of 1! 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 5

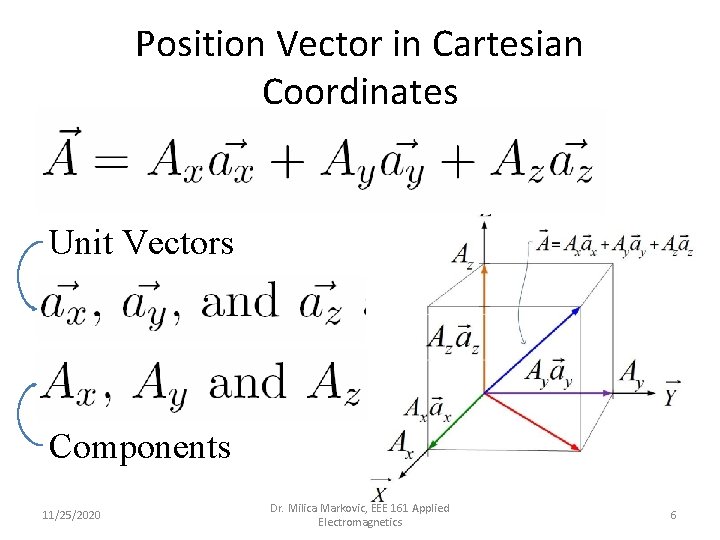
Position Vector in Cartesian Coordinates Unit Vectors Components 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 6

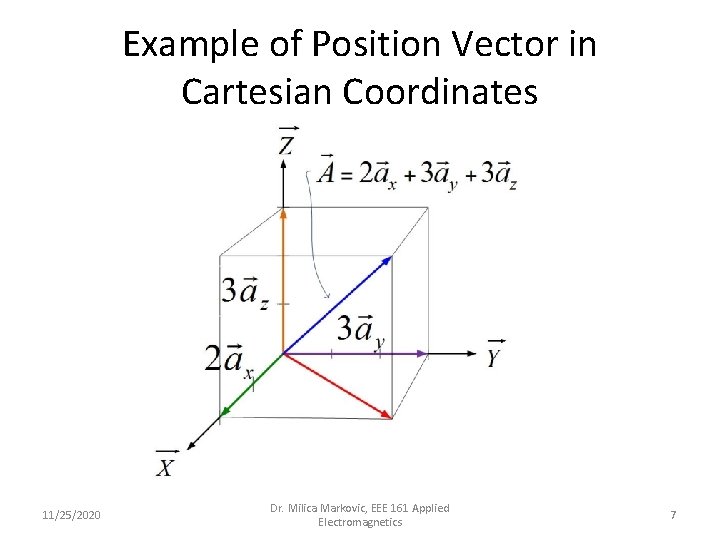
Example of Position Vector in Cartesian Coordinates 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 7

11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 8

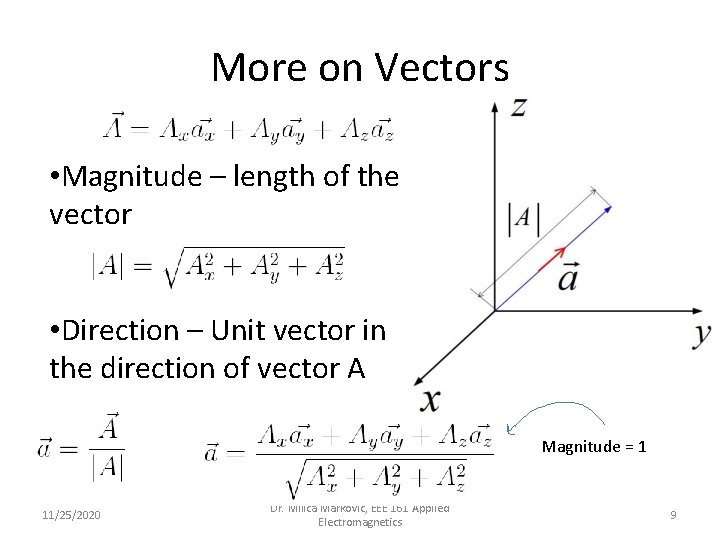
More on Vectors • Magnitude – length of the vector • Direction – Unit vector in the direction of vector A Magnitude = 1 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 9

Addition of Vectors • Head to Tail Rule • Parallelogram Rule 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 10

Negative Vector Negative Sign Changes Direction! 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 11

Subtraction of Vectors • First we change direction of vector B • Then we add A and –B up! 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 12

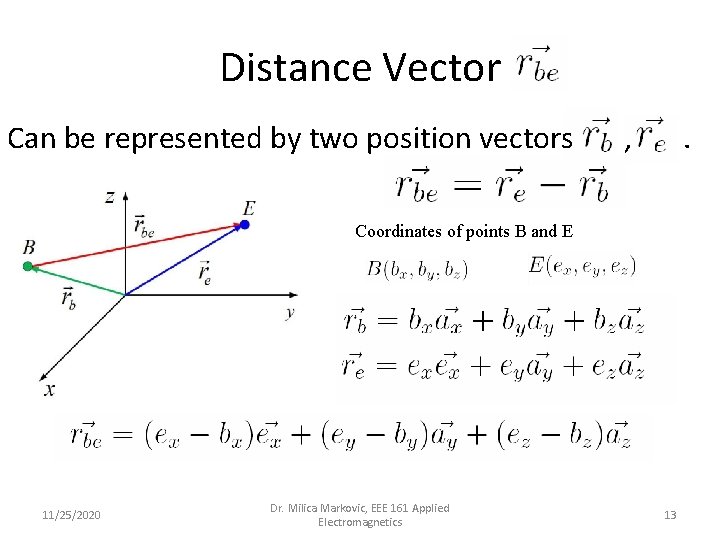
Distance Vector Can be represented by two position vectors , . Coordinates of points B and E 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 13

Distance Vector Magnitude and Unit Vector 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 14

Vector Multiplication • • Scalar or Dot Product Vector or Cross Product Scalar Triple Product Vector Triple Product 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 15

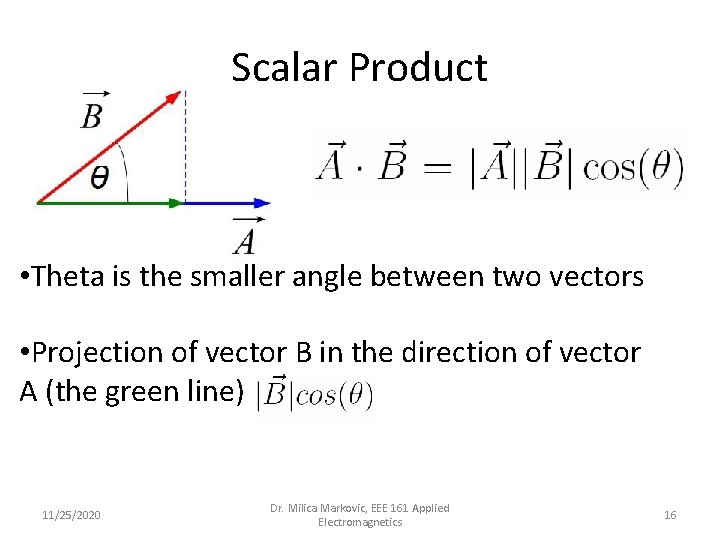
Scalar Product • Theta is the smaller angle between two vectors • Projection of vector B in the direction of vector A (the green line) 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 16

Scalar Product in Cartesian Coordinate System 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 17

5 -min Practice 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 18

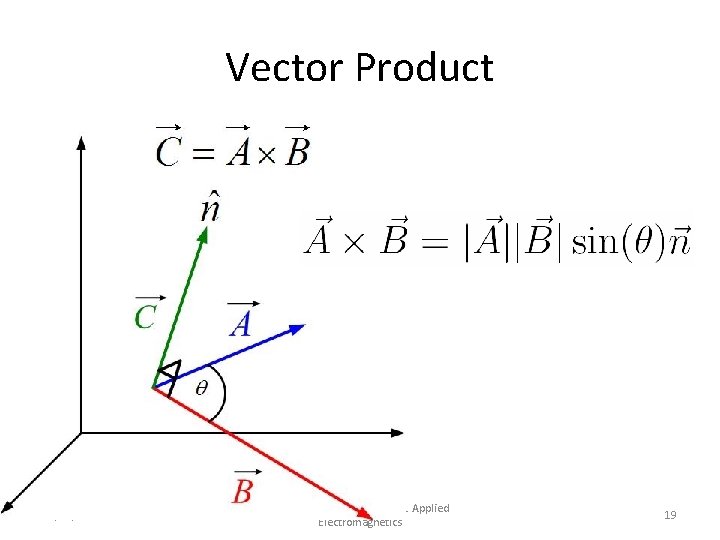
Vector Product 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 19

11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 20

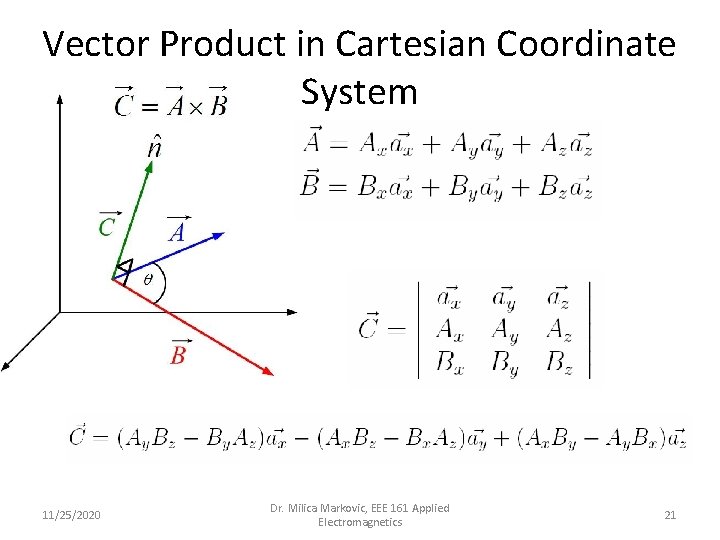
Vector Product in Cartesian Coordinate System 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 21

Properties of Cross Product 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 22

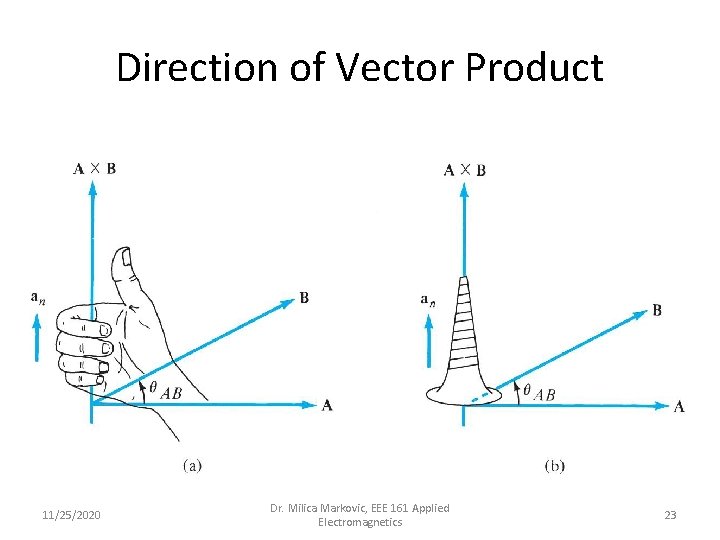
Direction of Vector Product 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 23

Chapters 2 and 3 COORDINATE SYSTEMS AND VECTOR CALCULUS 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 24

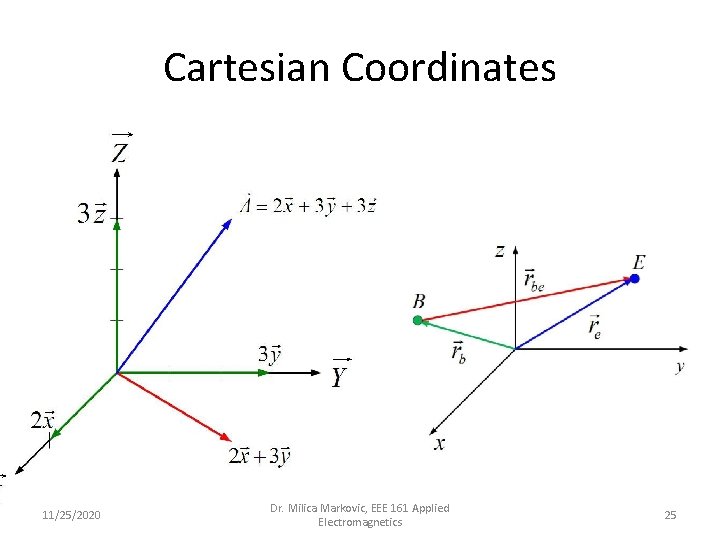
Cartesian Coordinates 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 25

Differential Length - Cart Coord 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 26

Differential Surface – Cart Coord 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 27

Differential Volume – Cart Coord Volume is base times height 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 28

Position Vector in Cylindrical Coordinates Three coordinates r, θ and z. Θ= 60 deg Position vector in Cylindrical Coordinates has only r and z directions! 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 29

11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 30

11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 31

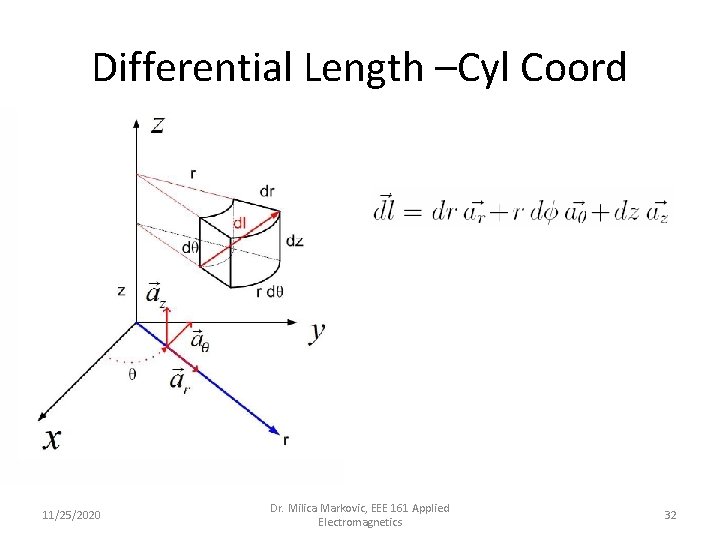
Differential Length –Cyl Coord 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 32

Differential Surface – Cyl Coord 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 33

Differential Volume Cyl Coord 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 34

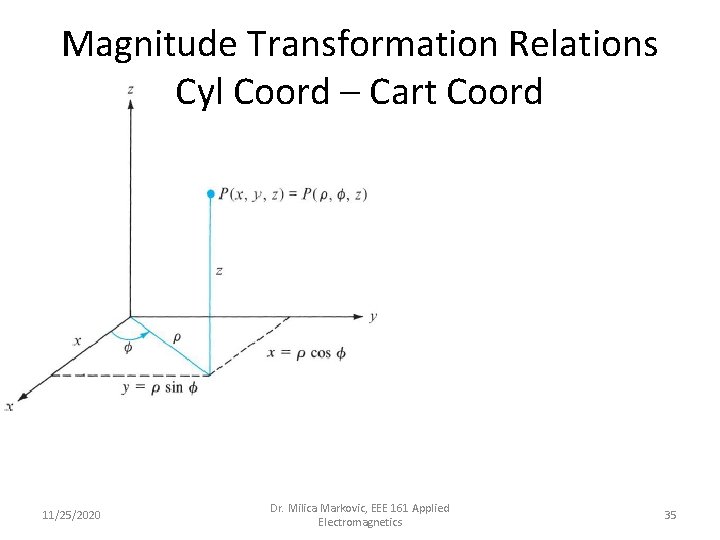
Magnitude Transformation Relations Cyl Coord – Cart Coord 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 35

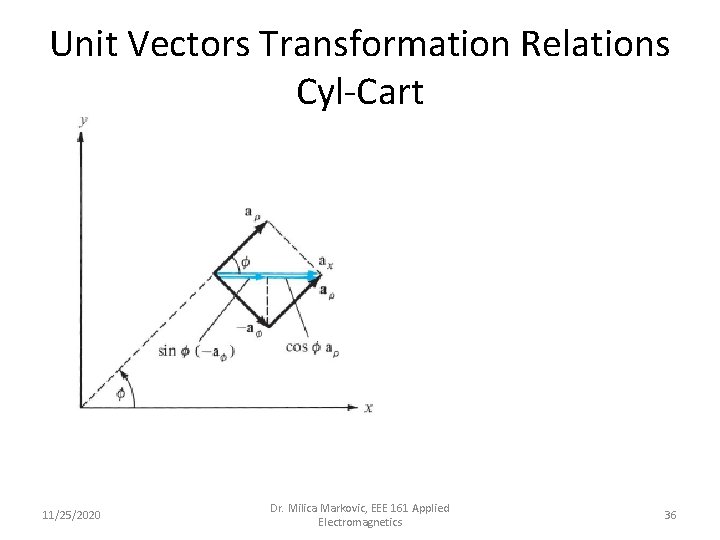
Unit Vectors Transformation Relations Cyl-Cart 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 36

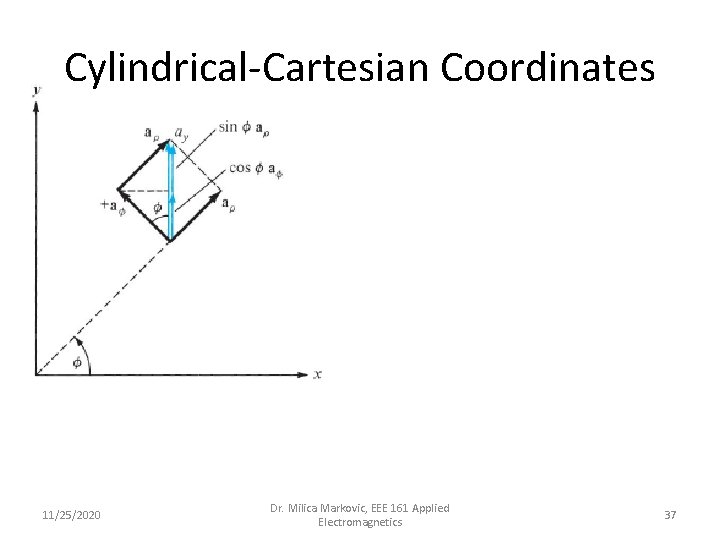
Cylindrical-Cartesian Coordinates 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 37

Position Vector in Spherical Coordinates Three coordinates r, θ and Φ. Position vector in Cylindrical Coordinates is only in the R direction! 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 38

Differential Length – Spherical Coord. 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 39

Differential Surface – Spher. Coord 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 40

Differential Volume- Spher Coord 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 41

Distance Between Two Points 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 42

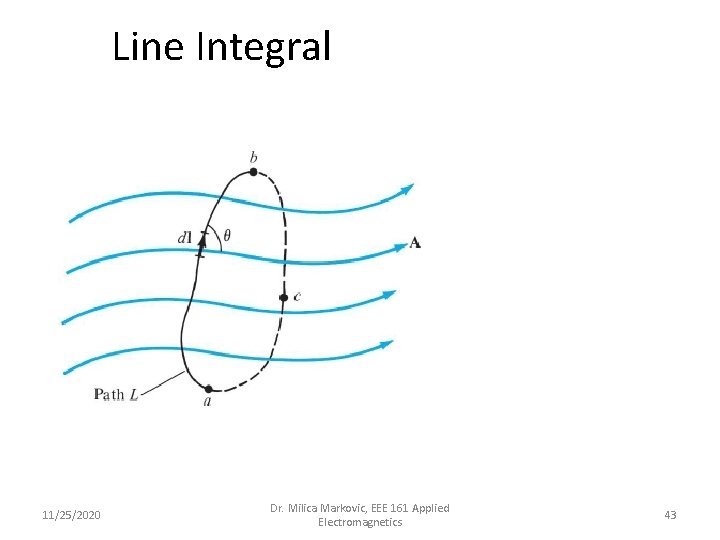
Line Integral 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 43

Surface Integral 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 44

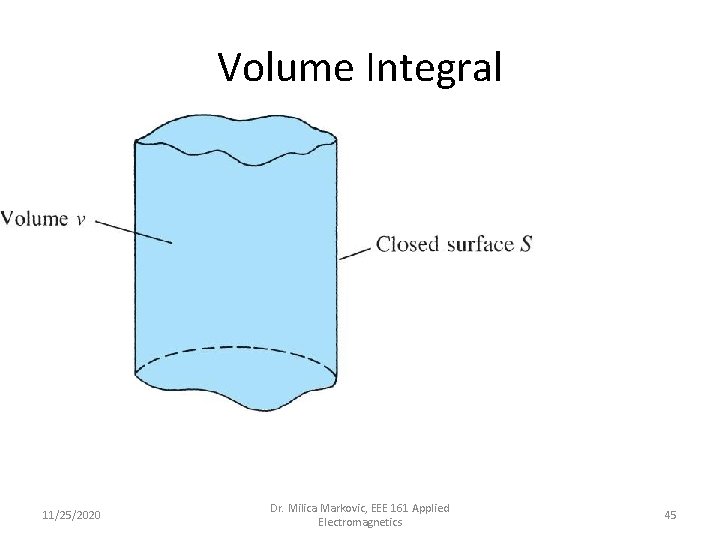
Volume Integral 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 45

Representation of Vector Fields are usually represented by arrows. 1. The stronger the field at a point the longer the vector at the point. 2. The stronger the field in an area the higher the density of vectors in that area. All vectors have the same magnitude. 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 46

A Del Operator Del operator is used to define 1. Gradient 2. Divergence 3. Laplacian 4. Curl. 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 47

11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 48

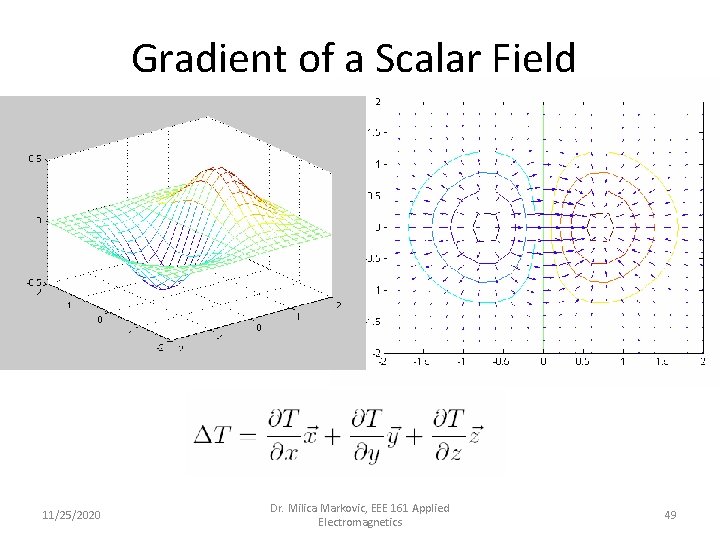
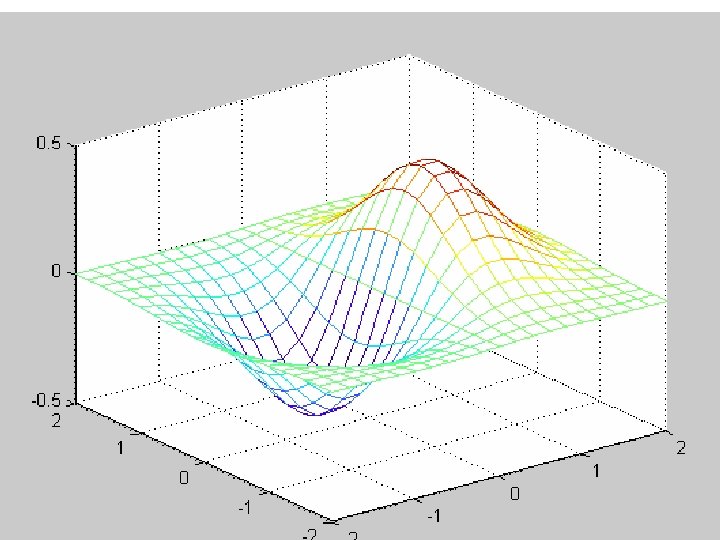
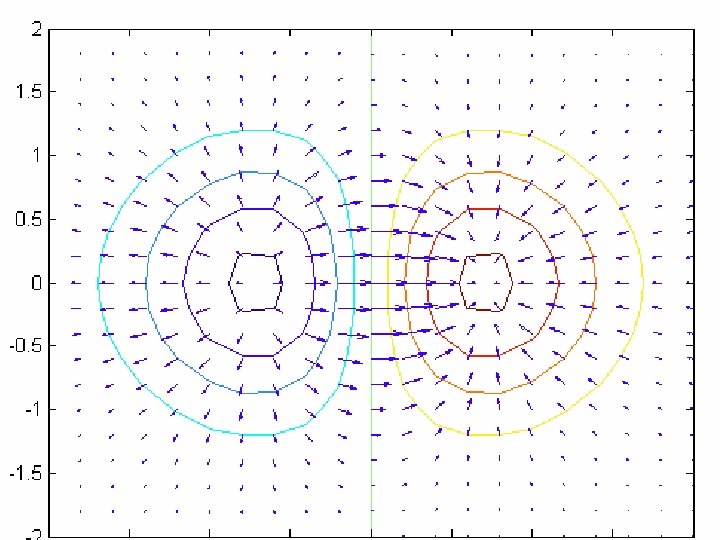
Gradient of a Scalar Field 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 49

11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 50

11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 51

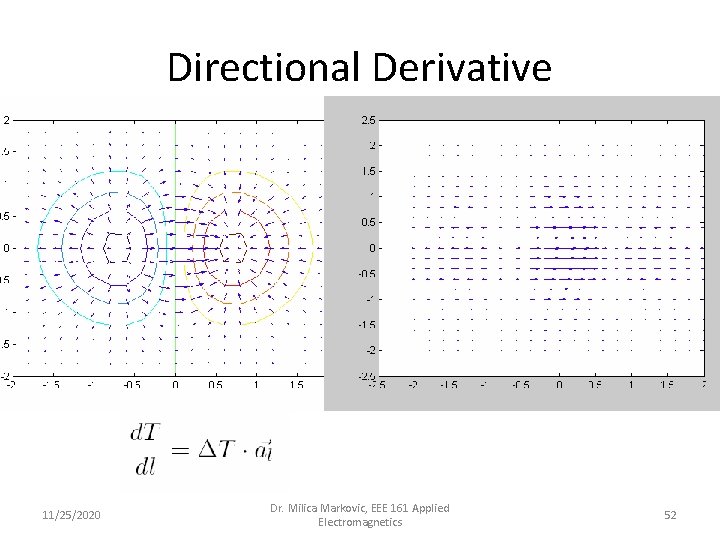
Directional Derivative 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 52

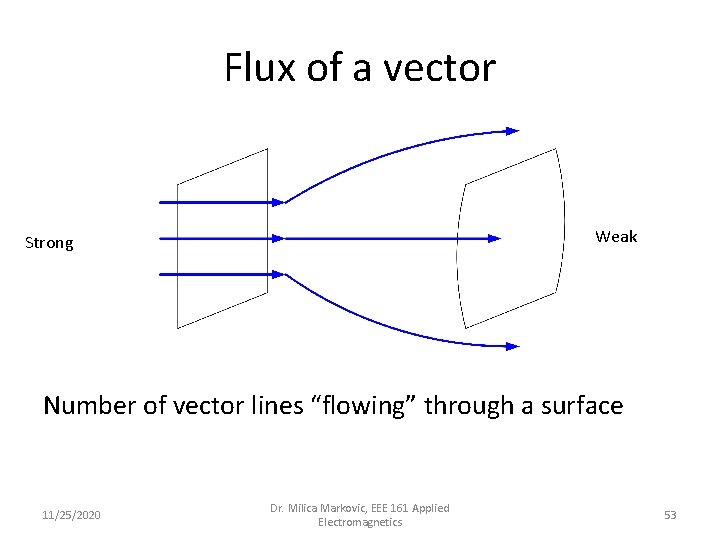
Flux of a vector Weak Strong Number of vector lines “flowing” through a surface 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 53

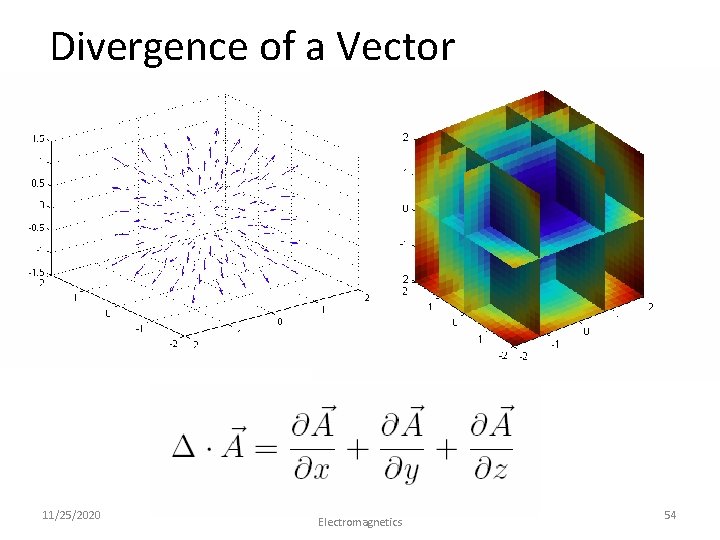
Divergence of a Vector 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 54

Divergence Theorem Flux through a closed surface 11/25/2020 Volume integral thorough of divergence over a volume ~ this is usually easier to find. Dr. Milica Markovic, EEE 161 Applied Electromagnetics 55

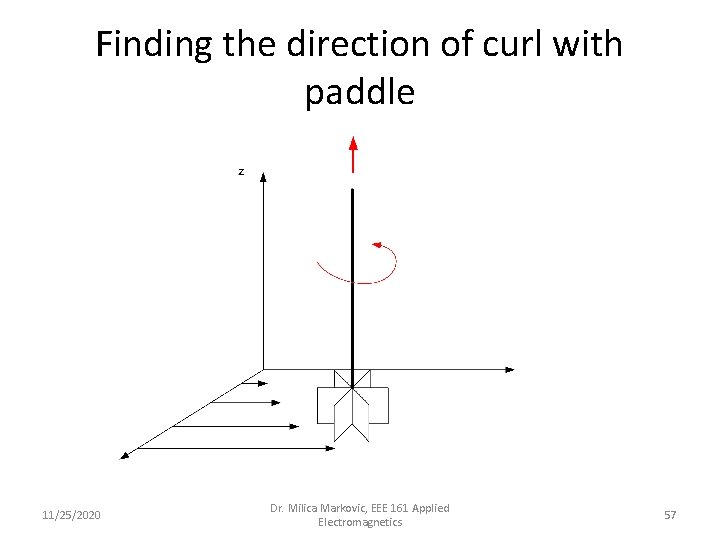
Curl of a Vector = Rotation (Curling) of Field Direction perpendicular to vector field. 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 56

Finding the direction of curl with paddle 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 57

Stoke’s Theorem Circulation of vector A 11/25/2020 Surface integral of the curl of A over the surface bounded by S Dr. Milica Markovic, EEE 161 Applied Electromagnetics 58

Laplacian of a Scalar Divergence of Gradient Scalar field is harmonic if: (Laplace’s Equation) 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 59

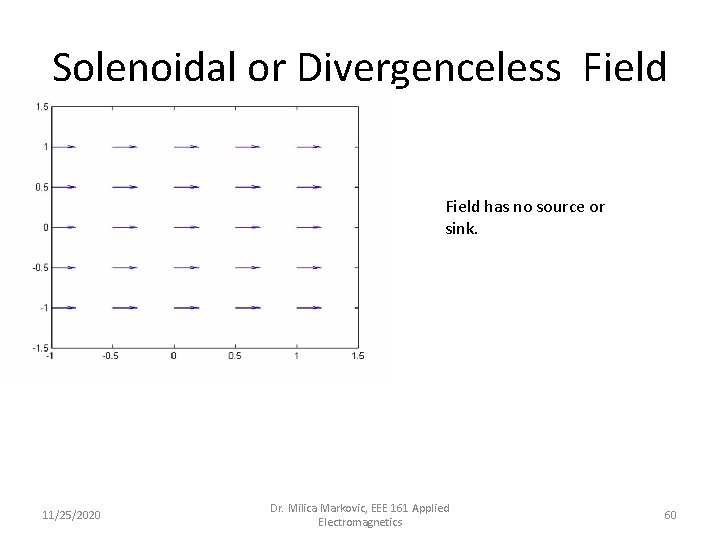
Solenoidal or Divergenceless Field has no source or sink. 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 60

Irrotational or Potential Field 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 61

11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 62

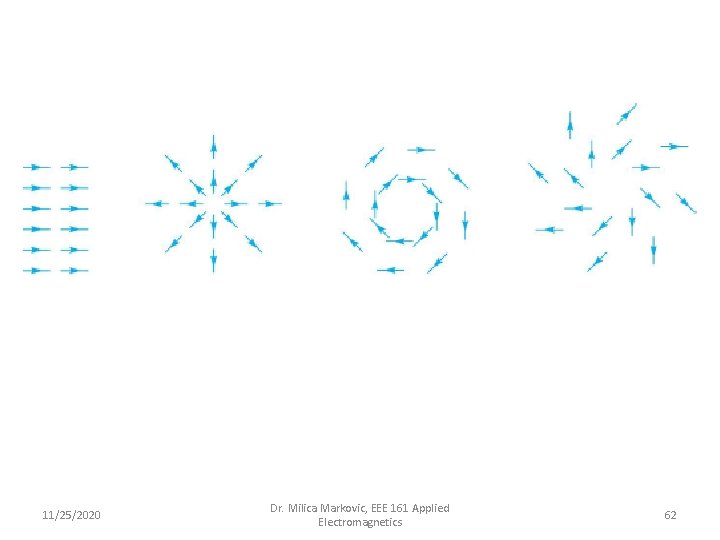
Classification of Vector Fields 11/25/2020 Dr. Milica Markovic, EEE 161 Applied Electromagnetics 63

1. 2. 3. 4. 5. 6. 7. 11/25/2020 Why isn’t del D equal to zero If the curl is zero is the field not spinning Issue with D If the curl and divergence are zero what’s happening Is the curl of C positive or negative Are you using the density or length notation Can we write del cross A =magnitude del magn Dr. Milica Markovic, EEE 161 Applied Electromagnetics 64