EECE 320 Digital Systems Design Lecture 5 Combinational

EECE 320 Digital Systems Design Lecture 5: Combinational Logic Design Principles Ali Chehab EECE 320 L 5: Combinational Logic design Principles 1 Chehab, AUB, 2003

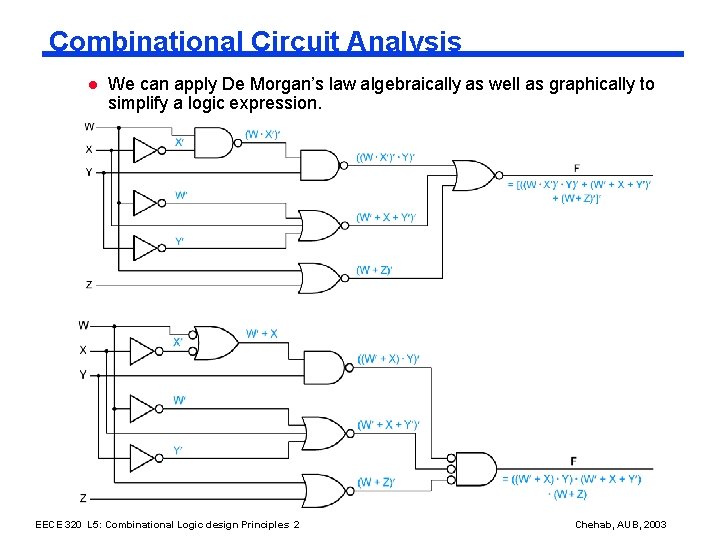
Combinational Circuit Analysis l We can apply De Morgan’s law algebraically as well as graphically to simplify a logic expression. EECE 320 L 5: Combinational Logic design Principles 2 Chehab, AUB, 2003

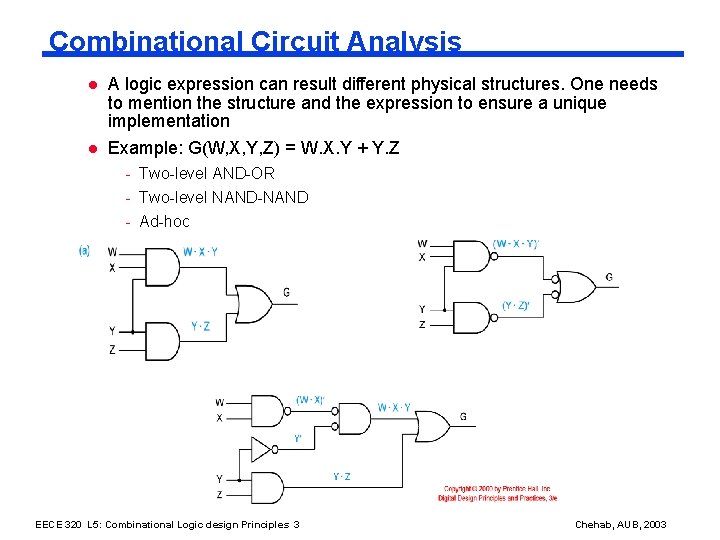
Combinational Circuit Analysis l l A logic expression can result different physical structures. One needs to mention the structure and the expression to ensure a unique implementation Example: G(W, X, Y, Z) = W. X. Y + Y. Z - Two-level AND-OR - Two-level NAND-NAND - Ad-hoc EECE 320 L 5: Combinational Logic design Principles 3 Chehab, AUB, 2003

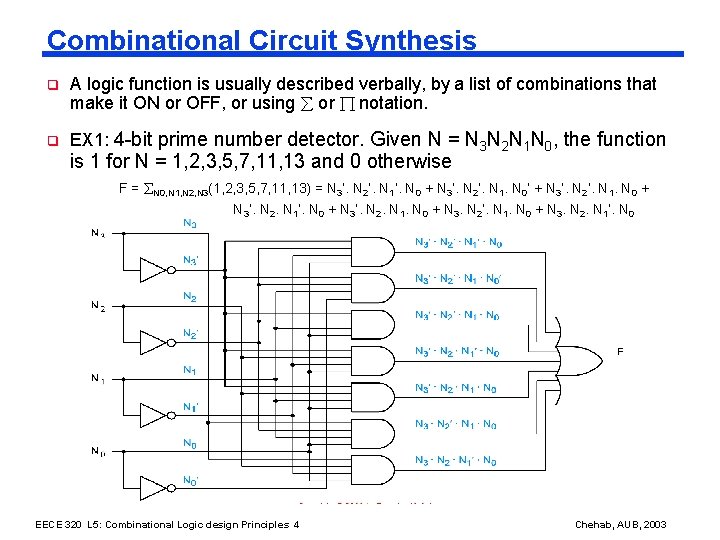
Combinational Circuit Synthesis q A logic function is usually described verbally, by a list of combinations that make it ON or OFF, or using or notation. q EX 1: 4 -bit prime number detector. Given N = N 3 N 2 N 1 N 0, the function is 1 for N = 1, 2, 3, 5, 7, 11, 13 and 0 otherwise F = N 0, N 1, N 2, N 3(1, 2, 3, 5, 7, 11, 13) = N 3’. N 2’. N 1’. N 0 + N 3’. N 2’. N 1. N 0’ + N 3’. N 2’. N 1. N 0 + N 3’. N 2. N 1’. N 0 + N 3’. N 2. N 1. N 0 + N 3. N 2’. N 1. N 0 + N 3. N 2. N 1’. N 0 EECE 320 L 5: Combinational Logic design Principles 4 Chehab, AUB, 2003

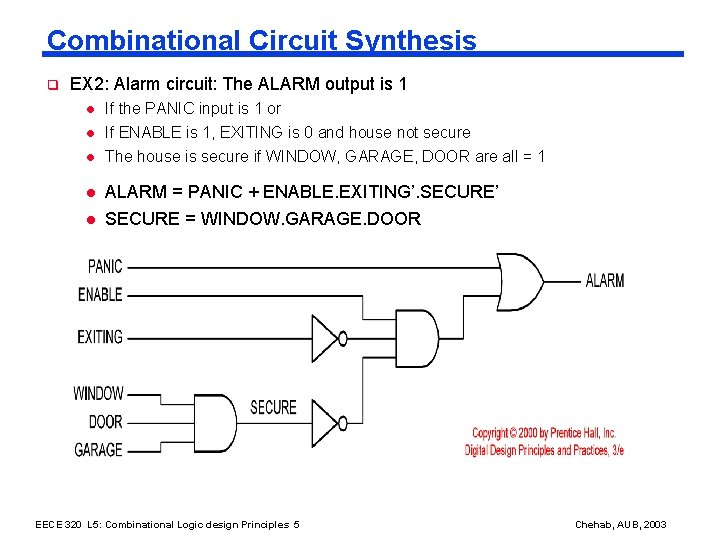
Combinational Circuit Synthesis q EX 2: Alarm circuit: The ALARM output is 1 l If the PANIC input is 1 or l l If ENABLE is 1, EXITING is 0 and house not secure The house is secure if WINDOW, GARAGE, DOOR are all = 1 l ALARM = PANIC + ENABLE. EXITING’. SECURE’ l SECURE = WINDOW. GARAGE. DOOR EECE 320 L 5: Combinational Logic design Principles 5 Chehab, AUB, 2003

Combinational Circuit Minimization q We can Minimize a combinational circuit by reducing the number and size of gates that are needed to build the circuit. q Minimization methods reduce a 2 -level implementation by: 1. Minimizing the number of first level gates 2. Minimizing the number of inputs on each first-level gate 3. Minimizing the number of inputs on the second-level gate l They are mainly based on combining theorems (T 10) and (T 10’) l (T 10) X. Y + X. Y’ = X l EX: Prime Number Detector, F = A’. B’. C’. D + A’. B’. C. D’ + A’. B’. C. D + l EECE 320 L 5: Combinational Logic design Principles 6 (T 10’) (X+Y). (X+Y’) = X A’. B. C’. D + A’. B. C. D + A. B’. C. D + A. B. C’. D Chehab, AUB, 2003

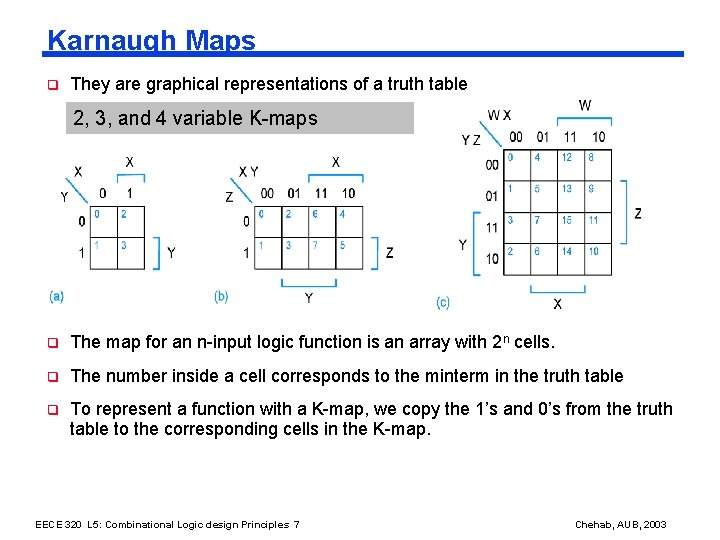
Karnaugh Maps q They are graphical representations of a truth table 2, 3, and 4 variable K-maps q The map for an n-input logic function is an array with 2 n cells. q The number inside a cell corresponds to the minterm in the truth table q To represent a function with a K-map, we copy the 1’s and 0’s from the truth table to the corresponding cells in the K-map. EECE 320 L 5: Combinational Logic design Principles 7 Chehab, AUB, 2003

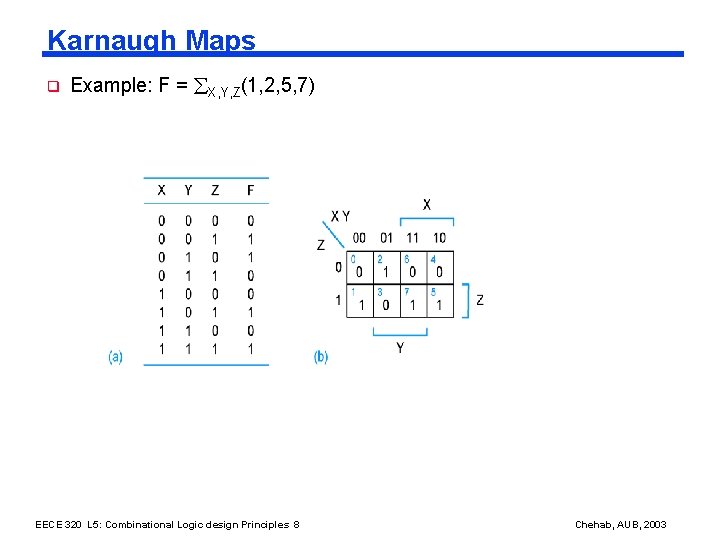
Karnaugh Maps q Example: F = X, Y, Z(1, 2, 5, 7) EECE 320 L 5: Combinational Logic design Principles 8 Chehab, AUB, 2003

Next Lecture and Reminders q Next lecture q Reminders EECE 320 L 5: Combinational Logic design Principles 9 Chehab, AUB, 2003