EE194 PLA Introduction to Plasma Engineering Part 1

EE-194 -PLA Introduction to Plasma Engineering Part 1: Plasma Technology Part 2: Vacuum Basics Part 3: Plasma Overview Professor Jeff Hopwood ECE Dept. , Tufts University

Part 1: Basic Plasma Technology

Plasma: an ionized gas consisting of atoms, electrons, ions, molecules, molecular fragments, and electronically excited species (informal definition) www. geo. mtu. edu/weather/aurora/

Plasma: the “fourth state of matter” plasma energy (electrons+ions) gas (steam) solid (ice) energy liquid (water)

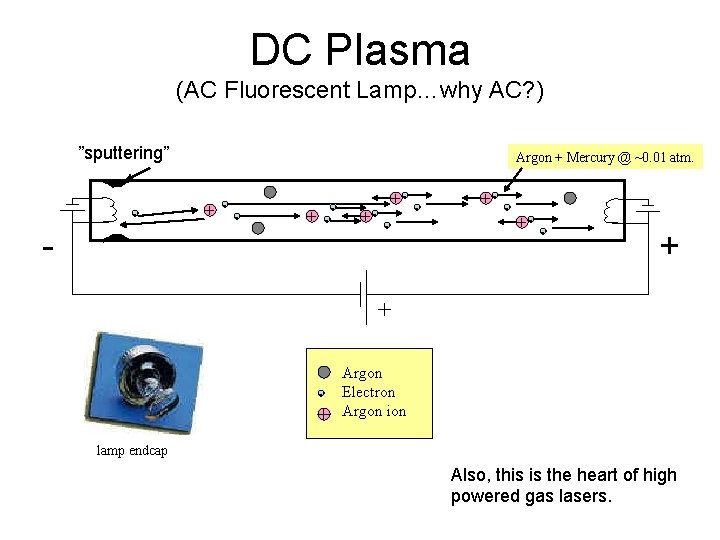
DC Plasma (AC Fluorescent Lamp…why AC? ) ”sputtering” - - Argon + Mercury @ ~0. 01 atm. + - - +- +- - + + - + Argon Electron Argon ion lamp endcap Also, this is the heart of high powered gas lasers.

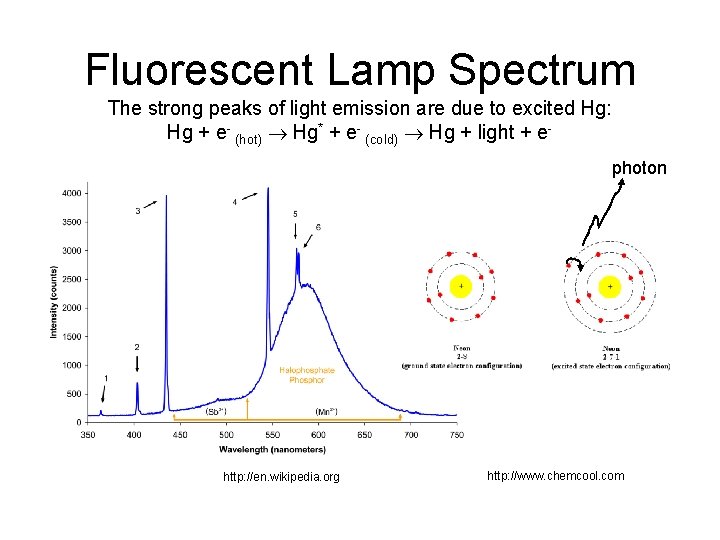
Fluorescent Lamp Spectrum The strong peaks of light emission are due to excited Hg: Hg + e- (hot) Hg* + e- (cold) Hg + light + ephoton http: //en. wikipedia. org http: //www. chemcool. com

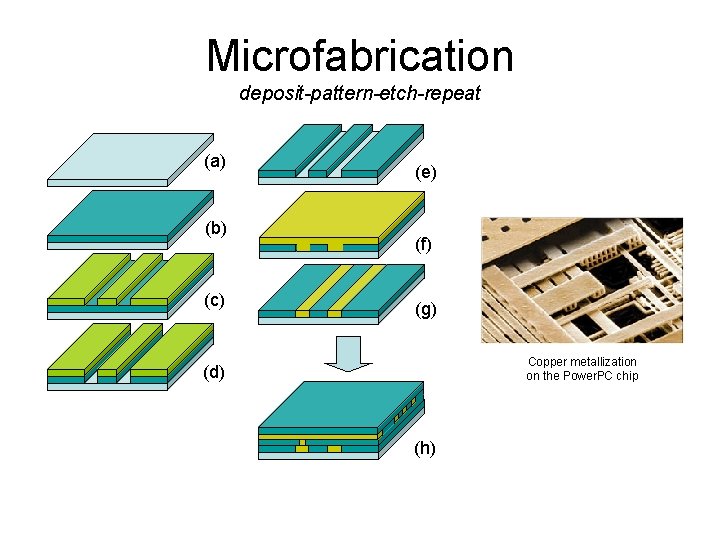
Integrated Circuit Fabrication and Plasma Technology

Microfabrication deposit-pattern-etch-repeat (a) (b) (c) (e) (f) (g) Copper metallization on the Power. PC chip (d) (h)

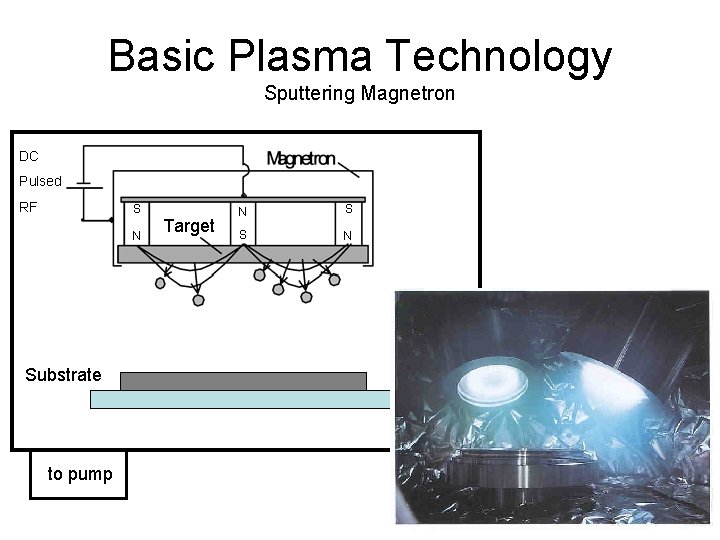
Basic Plasma Technology Sputtering Magnetron DC Pulsed RF S N Substrate to pump Target N S S N

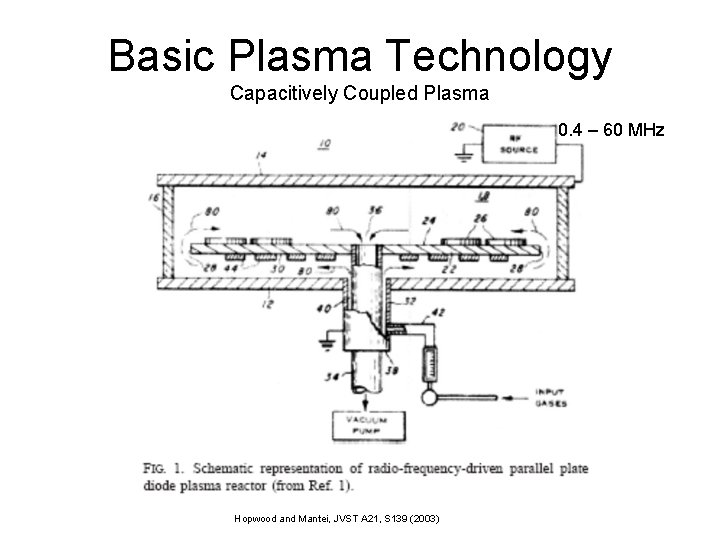
Basic Plasma Technology Capacitively Coupled Plasma 0. 4 – 60 MHz Hopwood and Mantei, JVST A 21, S 139 (2003)

Plasma Etching Cl 2 Cl+ Si. Cl 2 Cl S Cl 2 Simplified anisotropic etching Cl 2 + e- Cl + Cl+ + 2 e. Si(s) + 2 Cl(g)+ ion energy Si. Cl 2(g)

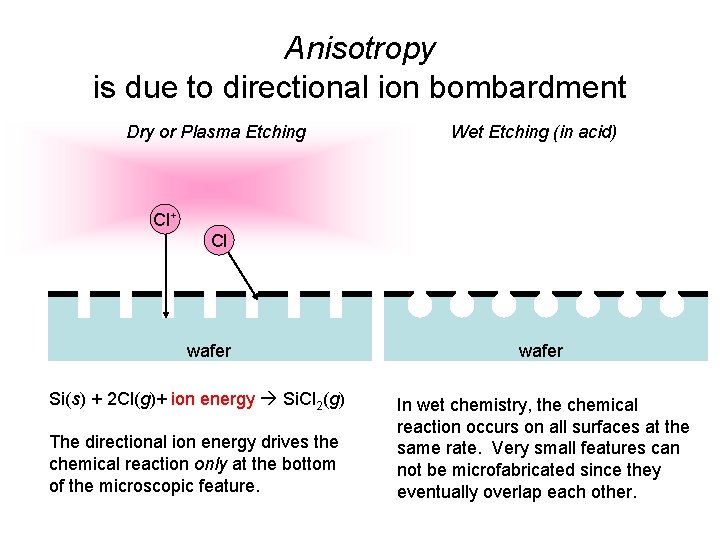
Anisotropy is due to directional ion bombardment Dry or Plasma Etching Wet Etching (in acid) Cl+ Cl wafer Si(s) + 2 Cl(g)+ ion energy Si. Cl 2(g) The directional ion energy drives the chemical reaction only at the bottom of the microscopic feature. wafer In wet chemistry, the chemical reaction occurs on all surfaces at the same rate. Very small features can not be microfabricated since they eventually overlap each other.

Trenches: etched and filled with copper Jason M. Blackburn, David P. Long, Albertina Cabañas, James J. Watkins Science 5 October 2001: Vol. 294. no. 5540, pp. 141 - 145

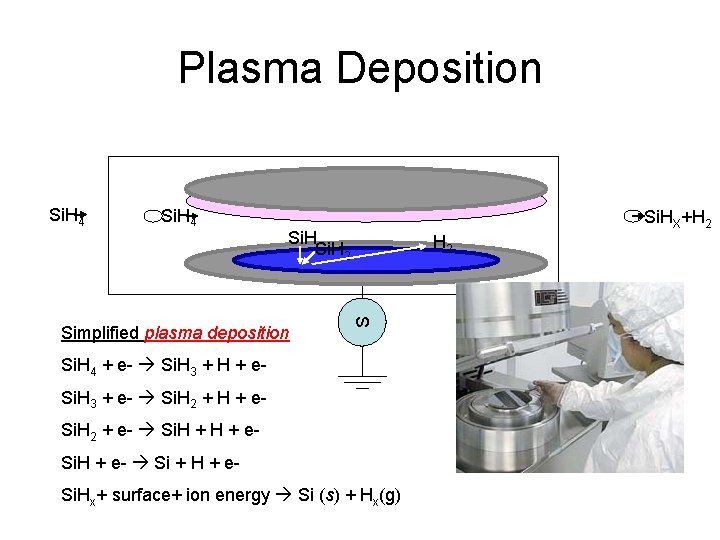
Plasma Deposition Si. H 4 Si. HX+H 2 Simplified plasma deposition H 2 S Si. H 4 + e- Si. H 3 + H + e. Si. H 3 + e- Si. H 2 + H + e. Si. H 2 + e- Si. H + e- Si + H + e. Si. Hx+ surface+ ion energy Si (s) + Hx(g)

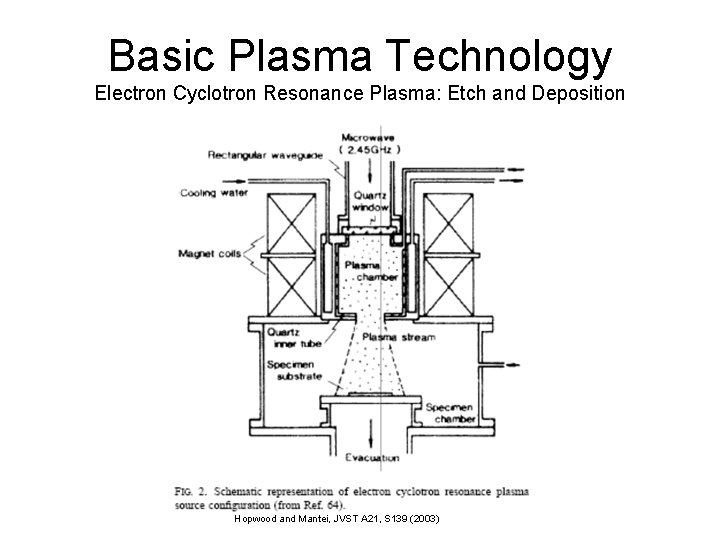
Basic Plasma Technology Electron Cyclotron Resonance Plasma: Etch and Deposition Hopwood and Mantei, JVST A 21, S 139 (2003)

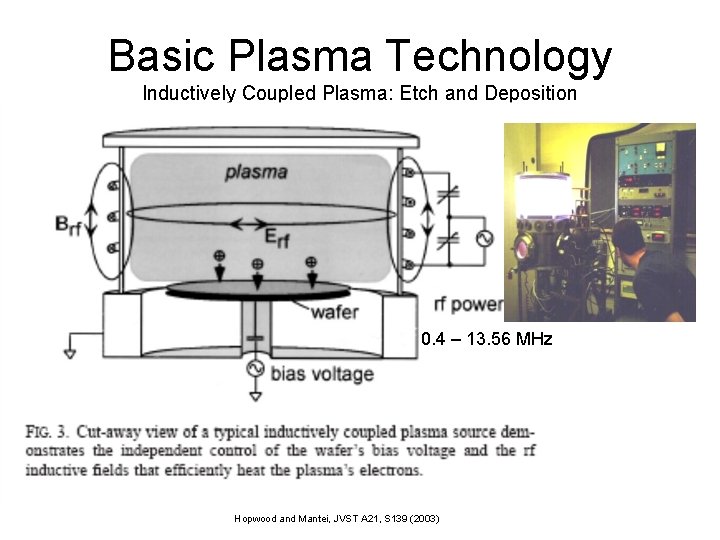
Basic Plasma Technology Inductively Coupled Plasma: Etch and Deposition 0. 4 – 13. 56 MHz Hopwood and Mantei, JVST A 21, S 139 (2003)

Other applications: Xenon Ion Propulsion Deep Space 1 encounter with Comet Borrelly http: //nmp. nasa. gov/ds 1/images. html

Other Applications : Plasma Display Panels (PDPs) Structure blue red green From S. S. Yang, et al, IEEE Trans. Plasma Sci. 31, 596 (2003).

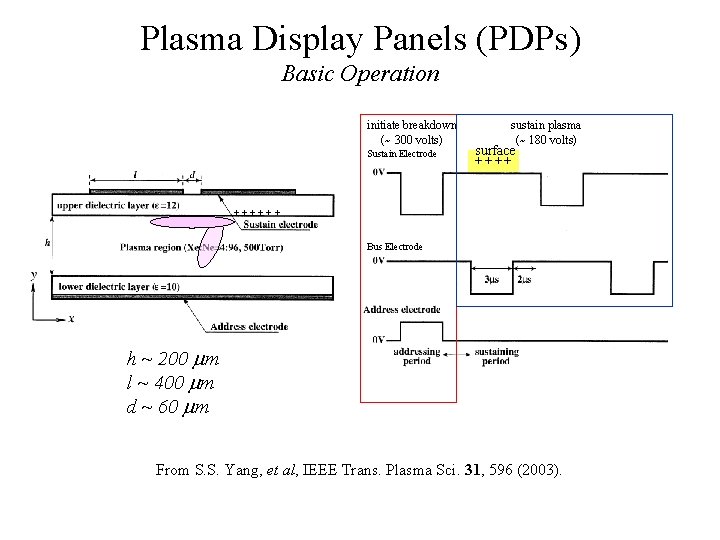
Plasma Display Panels (PDPs) Basic Operation initiate breakdown (~ 300 volts) Sustain Electrode sustain plasma (~ 180 volts) surface ++++++ Bus Electrode h ~ 200 m l ~ 400 m d ~ 60 m From S. S. Yang, et al, IEEE Trans. Plasma Sci. 31, 596 (2003).

Part 2: Basic Vacuum Concepts

Goals • To review basic vacuum technology – Pressure, pumps, gauges • To review gas flow and conductance • To understand the flux of vapor phase material to a substrate • To understand mean free path, l

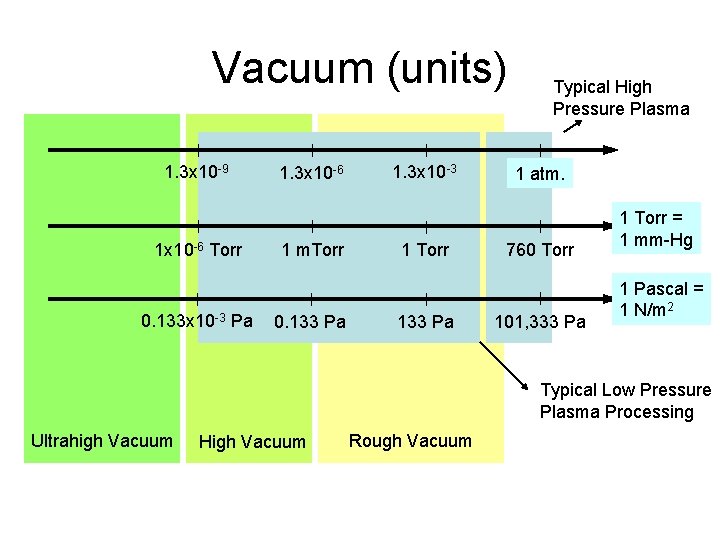
Vacuum (units) 1. 3 x 10 -9 1 x 10 -6 Torr 0. 133 x 10 -3 Pa 1. 3 x 10 -6 1 m. Torr 0. 133 Pa 1. 3 x 10 -3 1 Torr 133 Pa Typical High Pressure Plasma 1 atm. 760 Torr 101, 333 Pa 1 Torr = 1 mm-Hg 1 Pascal = 1 N/m 2 Typical Low Pressure Plasma Processing Ultrahigh Vacuum High Vacuum Rough Vacuum

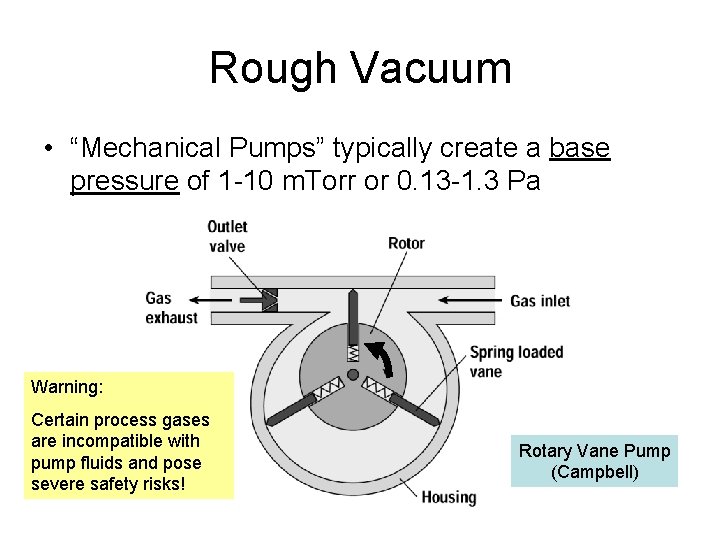
Rough Vacuum • “Mechanical Pumps” typically create a base pressure of 1 -10 m. Torr or 0. 13 -1. 3 Pa Warning: Certain process gases are incompatible with pump fluids and pose severe safety risks! Rotary Vane Pump (Campbell)

High Vacuum Pumping Cryopumps condense gases on cold surfaces to produce vacuum Typically there are three cold surfaces: (1) Inlet array condenses water and hydrocarbons (60 -100 Kelvin) (2) Condensing array pumps argon, nitrogen and most other gases (10 -20 K) (3) Adsorption is needed to trap helium, hydrogen and neon in activated carbon at 10 -12 K. These gases are pumped very slowly! (Campbell) Warning: all pumped gases are trapped inside the pump, so explosive, toxic and corrosive gases are not recommended. No mech. pump is needed until regen. adapted from www. helixtechnology. com

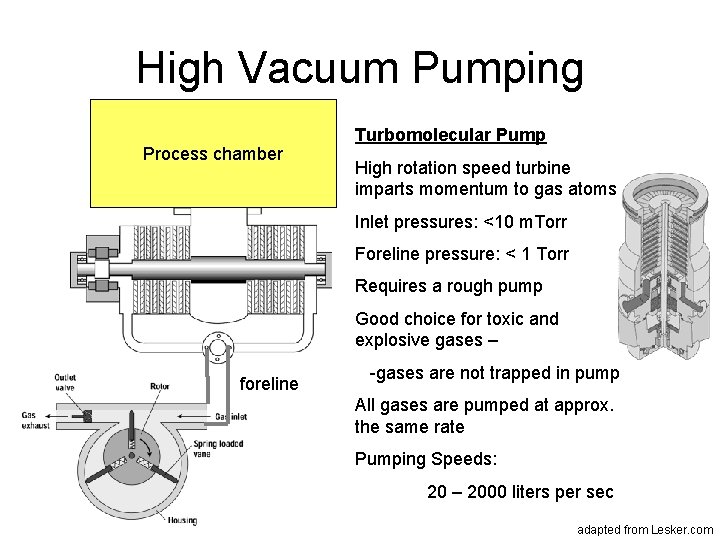
High Vacuum Pumping Process chamber Turbomolecular Pump High rotation speed turbine imparts momentum to gas atoms Inlet pressures: <10 m. Torr Foreline pressure: < 1 Torr Requires a rough pump Good choice for toxic and explosive gases – foreline -gases are not trapped in pump All gases are pumped at approx. the same rate Pumping Speeds: 20 – 2000 liters per sec adapted from Lesker. com

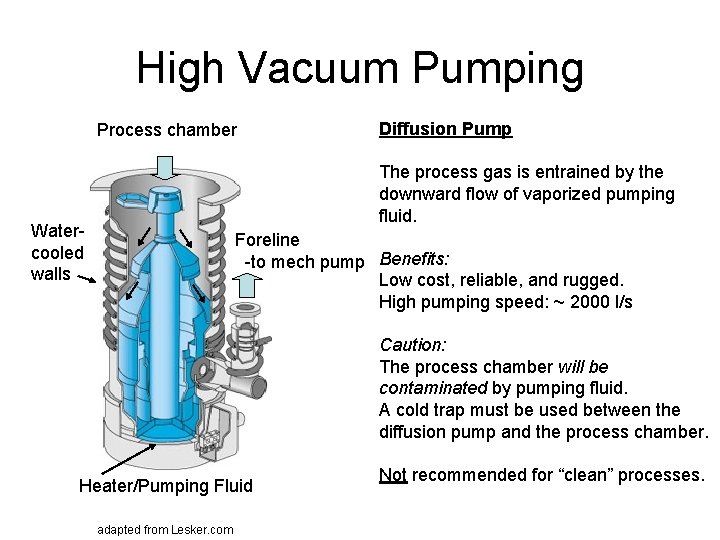
High Vacuum Pumping Process chamber Diffusion Pump The process gas is entrained by the downward flow of vaporized pumping fluid. Watercooled walls Foreline -to mech pump Benefits: Low cost, reliable, and rugged. High pumping speed: ~ 2000 l/s Caution: The process chamber will be contaminated by pumping fluid. A cold trap must be used between the diffusion pump and the process chamber. Heater/Pumping Fluid adapted from Lesker. com Not recommended for “clean” processes.

Flow Rate Typically gas flows are cited in units of standard cubic centimeters per minute (sccm) or standard liters per minute (slm) “Standard” refers to T=273 K, P = 1 atm. Example: Process gas flow of 50 sccm at 5 m. Torr (@300 K) requires 50 cm-3 min-1(760 Torr/5 x 10 -3 Torr)(300/273)(1 min/60 sec)(1/103) = 140 liters/sec of pumping speed at the chamber pump port

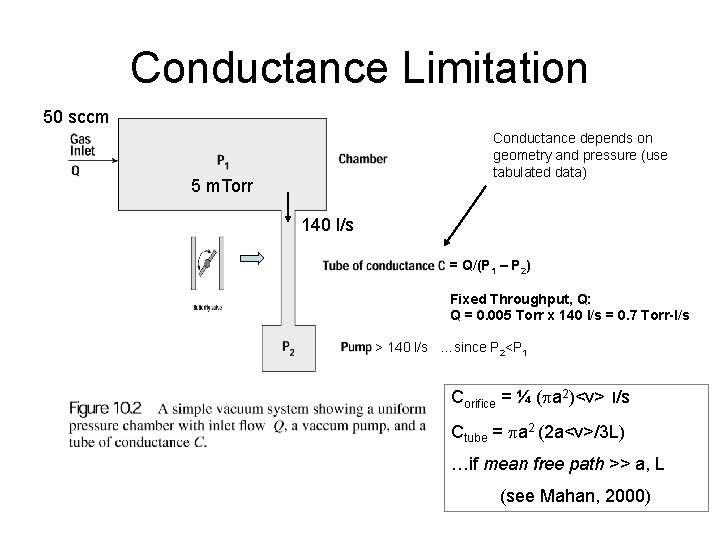
Conductance Limitation 50 sccm Conductance depends on geometry and pressure (use tabulated data) 5 m. Torr 140 l/s = Q/(P 1 – P 2) Fixed Throughput, Q: Q = 0. 005 Torr x 140 l/s = 0. 7 Torr-l/s > 140 l/s …since P 2<P 1 Corifice = ¼ (pa 2)<v> l/s Ctube = pa 2 (2 a<v>/3 L) …if mean free path >> a, L (see Mahan, 2000)

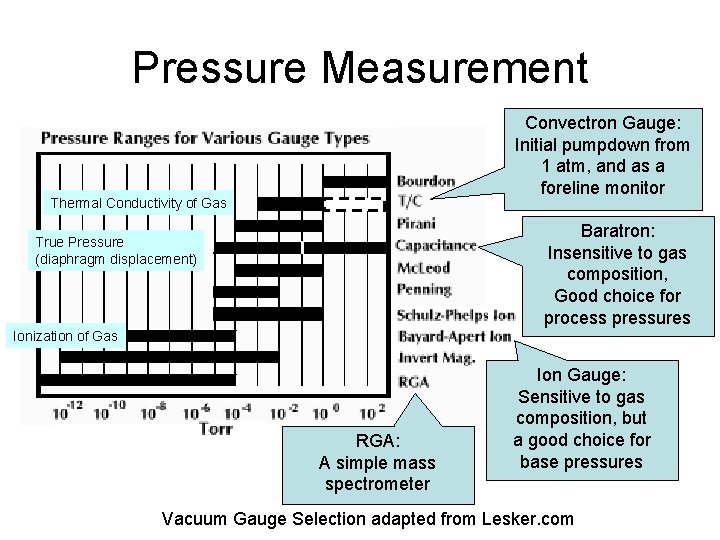
Pressure Measurement Convectron Gauge: Initial pumpdown from 1 atm, and as a foreline monitor Thermal Conductivity of Gas Baratron: Insensitive to gas composition, Good choice for process pressures True Pressure (diaphragm displacement) Ionization of Gas RGA: A simple mass spectrometer Ion Gauge: Sensitive to gas composition, but a good choice for base pressures Vacuum Gauge Selection adapted from Lesker. com

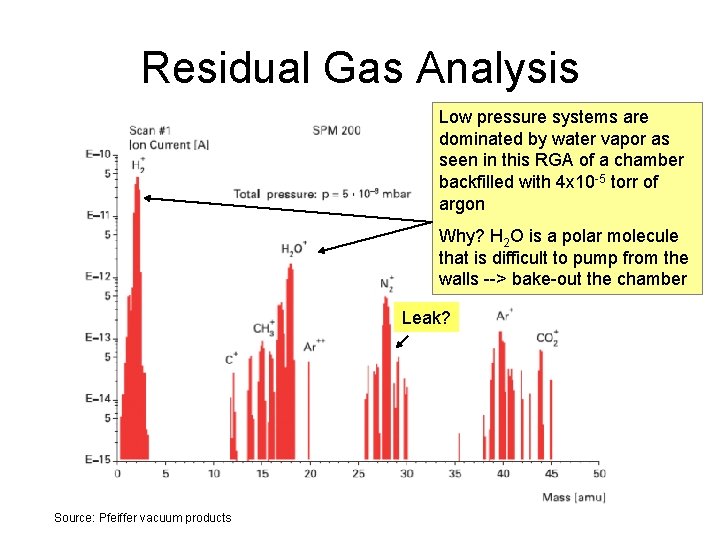
Residual Gas Analysis Low pressure systems are dominated by water vapor as seen in this RGA of a chamber backfilled with 4 x 10 -5 torr of argon Why? H 2 O is a polar molecule that is difficult to pump from the walls --> bake-out the chamber Leak? Source: Pfeiffer vacuum products

Gas Density (n) Ideal Gas Law PV = Nk. T Gas density at 1 Pascal at room temp. N/V = n = P/k. T = (1 N/m 2)/(1. 3807 x 10 -23 J/K)(300 K) = [1 (kg-m/s 2)/m 2]/[4. 1 x 10 -21 kg-m 2/s 2] = 2. 4 x 1020 atoms per m 3 = 2. 4 x 1014 cm-3 …at 1 Pa Rule of Thumb n(T) = 3. 2 x 1013 cm-3 x (300/T) …at a pressure of 1 m. Torr

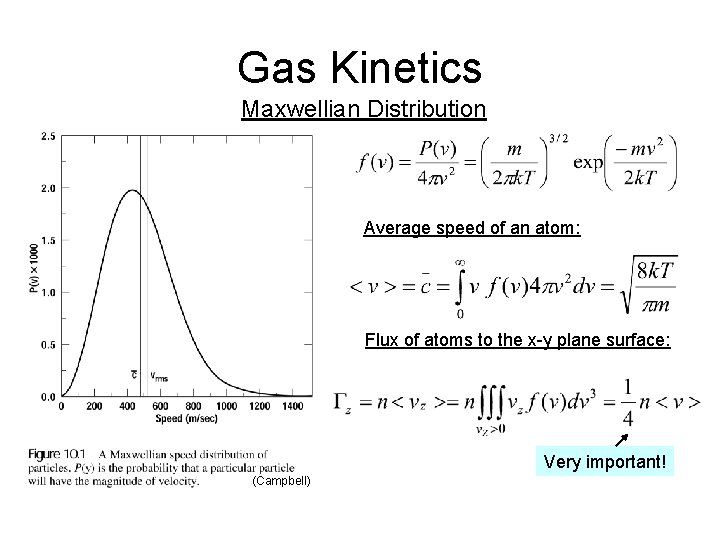
Gas Kinetics Maxwellian Distribution Average speed of an atom: Flux of atoms to the x-y plane surface: Very important! (Campbell)

Example A vacuum chamber has a base pressure of 10 -6 Torr. Assuming that this is dominated by water vapor, what is the flux of H 2 O to a substrate placed in this chamber? n = 3. 2 x 1013 cm-3/m. Torr * 10 -3 m. Torr = 3. 2 x 1010 cm-3 <v> = (8 k. T/p. M)1/2 = 59200 cm/s Gz = (¼)n<v> = 4. 74 x 1014 molecules per cm 2 per sec! This is approximately one monolayer of H 2 O every second at 10 -6 Torr base pressure.

Collisions and Mean Free Path Gas Density n = P/ k. T Cross-section s ~ p d 2 l = 1/sn d Rigorous Hard Sphere Collisions: l = k. T / 2 pd 2 P Ar l. Ar(cm) ~ 8 / P (m. Torr)

Part 3: Plasma Basics

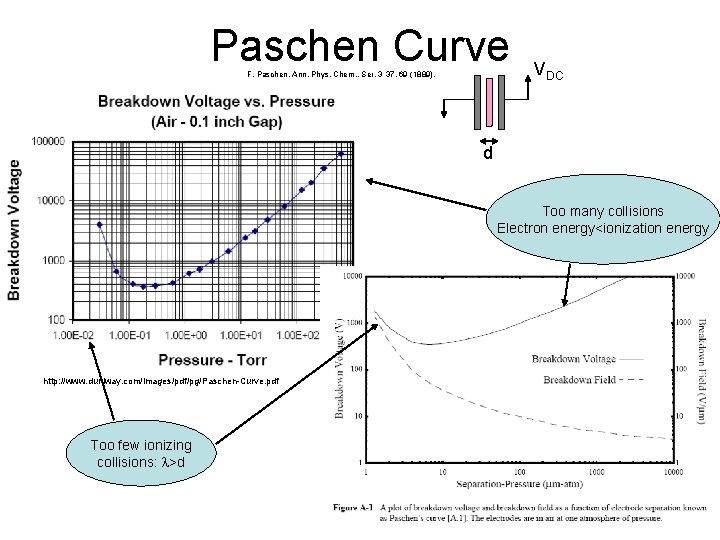
Paschen Curve F. Paschen, Ann. Phys. Chem. , Ser. 3 37, 69 (1889). VDC d Too many collisions Electron energy<ionization energy http: //www. duniway. com/images/pdf/pg/Paschen-Curve. pdf Too few ionizing collisions: l>d

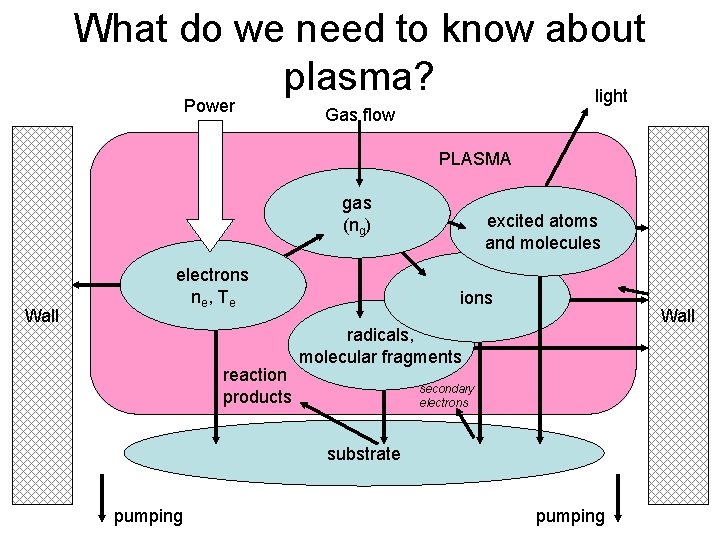
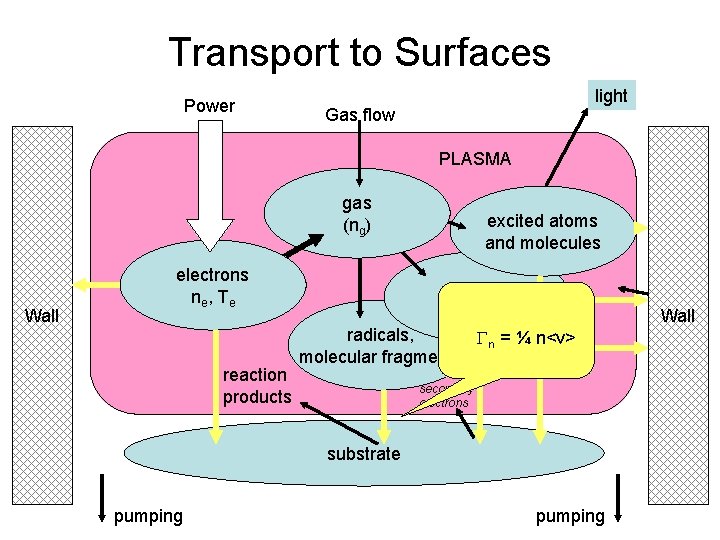
What do we need to know about plasma? light Power Gas flow PLASMA gas (ng) Wall electrons ne , T e reaction products excited atoms and molecules ions Wall radicals, molecular fragments secondary electrons substrate pumping

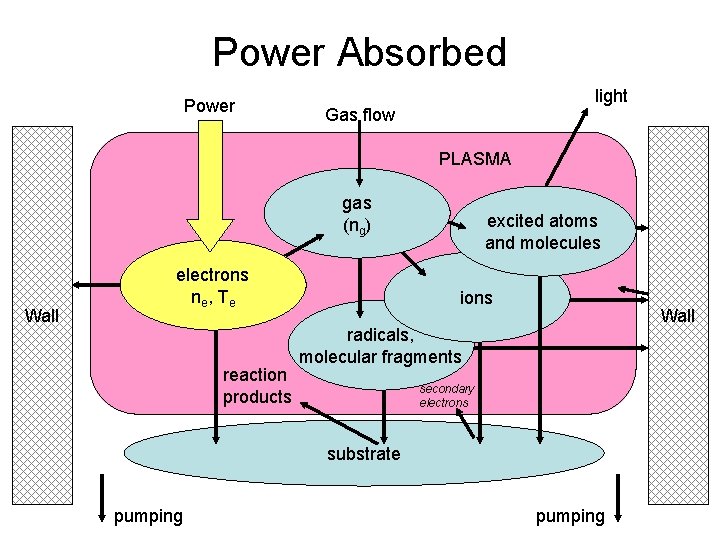
Power Absorbed Power light Gas flow PLASMA gas (ng) Wall electrons ne , T e reaction products excited atoms and molecules ions Wall radicals, molecular fragments secondary electrons substrate pumping

Power Absorbed: DC • DC power – General electrical mobility and conductivity – Mobility: me = q<t>/m = q/nmme Where <t> is the average time between collisions and nm is the collision frequency (collisions per second) – Electron Conductivity: s. DC = qne e = q 2 ne/nmme – DC power absorbed:

Power Absorbed: RF • RF/microwave power – Ohmic Heating VRF f=13. 56 MHz – Generic electron-neutral collision frequency nm ~ 5 x 10 -8 ngas. Te 1/2 (s-1) … ngas (cm-3), Te(e. V). – Example: Find the pressure at which rf ohmic heating becomes ineffective: nm = 0. 1 w, Te = 2 e. V w = 13. 56 MHz * 2 p = 85. 2 Mrad/s ngas = 0. 1*85. 2 x 106/5 x 10 -8(2)1/2 = 1. 2 x 1014 cm-3 = 3. 7 m. Torr An electron oscillates in a rf electric field without gaining energy unless electron collisions occur Hopwood and Mantei, JVST A 21, S 139 (2003)

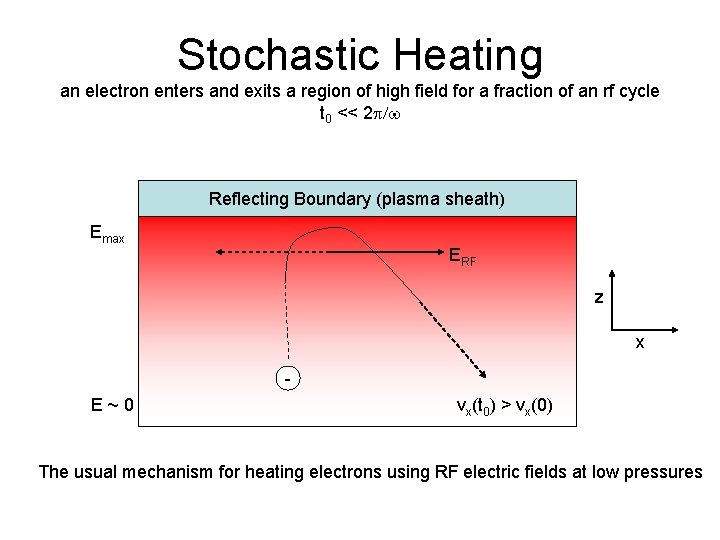
Stochastic Heating an electron enters and exits a region of high field for a fraction of an rf cycle t 0 << 2 p/w Reflecting Boundary (plasma sheath) Emax ERF z x - E~0 vx(t 0) > vx(0) The usual mechanism for heating electrons using RF electric fields at low pressures

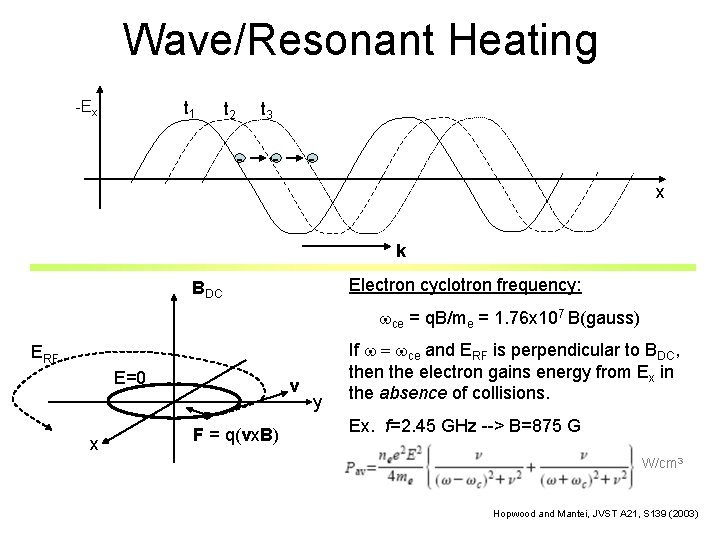
Wave/Resonant Heating -Ex t 1 t 3 t 2 - - x k Electron cyclotron frequency: BDC wce = q. B/me = 1. 76 x 107 B(gauss) ERF E=0 x v F = q(vx. B) y If w = wce and ERF is perpendicular to BDC, then the electron gains energy from Ex in the absence of collisions. Ex. f=2. 45 GHz --> B=875 G W/cm 3 Hopwood and Mantei, JVST A 21, S 139 (2003)

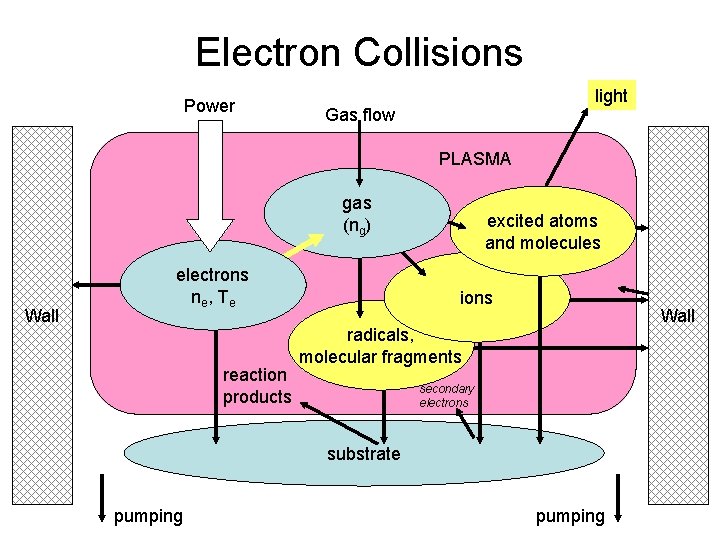
Electron Collisions Power light Gas flow PLASMA gas (ng) Wall electrons ne , T e reaction products excited atoms and molecules ions Wall radicals, molecular fragments secondary electrons substrate pumping

Electron Collisions • Elastic Collisions: – Ar + e – Gas heating: energy is coupled from e to the gas • Excitation Collisions – Ar + ehot Ar* + ecold, Ar* Ar + hn – Responsible for the characteristic plasma “glow” – Eelectron>Eexc (~11. 55 e. V for argon) • Ionization Collisions: – Ar + ehot Ar+ + 2 ecold – Couples electrical energy into producing more e_ – Eelectron > Eiz (15. 76 e. V for argon) • Dissociation: – O 2 + ehot 2 O + ecold or O 2 + ehot O + O+ + 2 ecold – Creates reactive chemical species within the plasma – Eelectron > Ediss (5. 12 e. V for oxygen)

Collision Cross Sections • Unlike the hard sphere model, real collision cross sections are a function of electron kinetic energy s(E), or electron velocity s(v). • We must find the expected collision frequency by averaging over all E or v. becomes (cm 3 s-1)

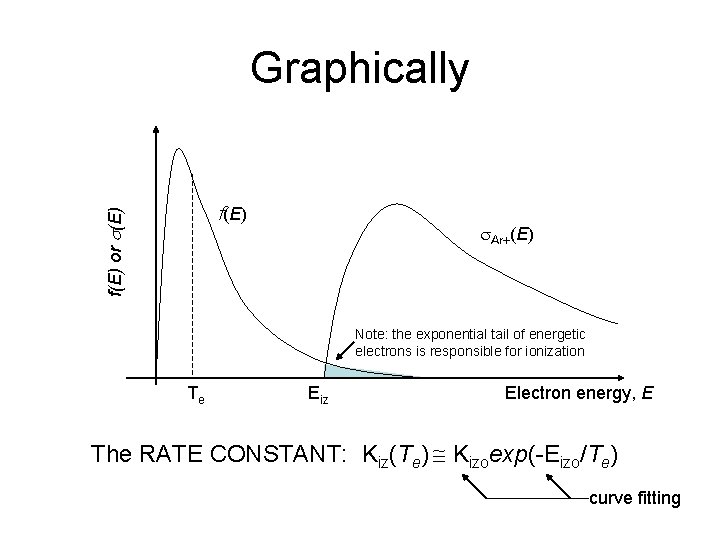
Graphically f(E) or s(E) f(E) s. Ar+(E) Note: the exponential tail of energetic electrons is responsible for ionization Te Eiz Electron energy, E The RATE CONSTANT: Kiz(Te) Kizoexp(-Eizo/Te) curve fitting

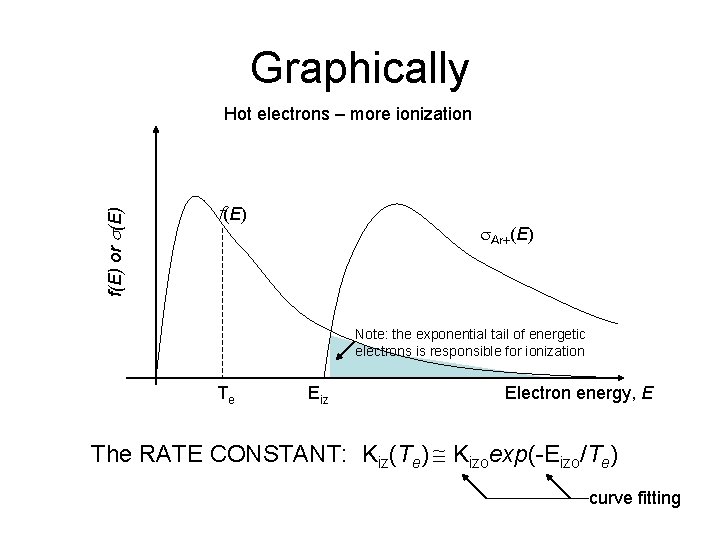
Graphically f(E) or s(E) Hot electrons – more ionization f(E) s. Ar+(E) Note: the exponential tail of energetic electrons is responsible for ionization Te Eiz Electron energy, E The RATE CONSTANT: Kiz(Te) Kizoexp(-Eizo/Te) curve fitting

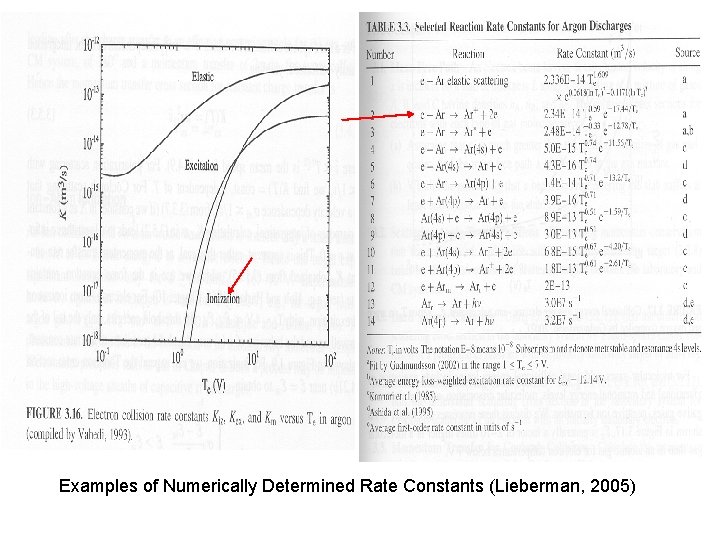
Examples of Numerically Determined Rate Constants (Lieberman, 2005)

Generation Rate of Plasma Species by Electron Collisions y+e x+e dnx/dt = Kxneny For example, e Ar+ + Ar + e+e dne/dt = Kiznengas is the number of electrons (and ions) generated per cm 3 per second

Electron-Ion Recombination Three-Body Problem: e + Ar+ + M Ar + M the third body is needed to conserve energy and momentum in the recombination process wall recombination - M volume recombination + M wall recombination dominates at low pressure because three body collisions are rare

Transport to Surfaces Power light Gas flow PLASMA gas (ng) Wall electrons ne , T e reaction products excited atoms and molecules ions radicals, Gn = ¼ n<v> molecular fragments secondary electrons substrate pumping Wall

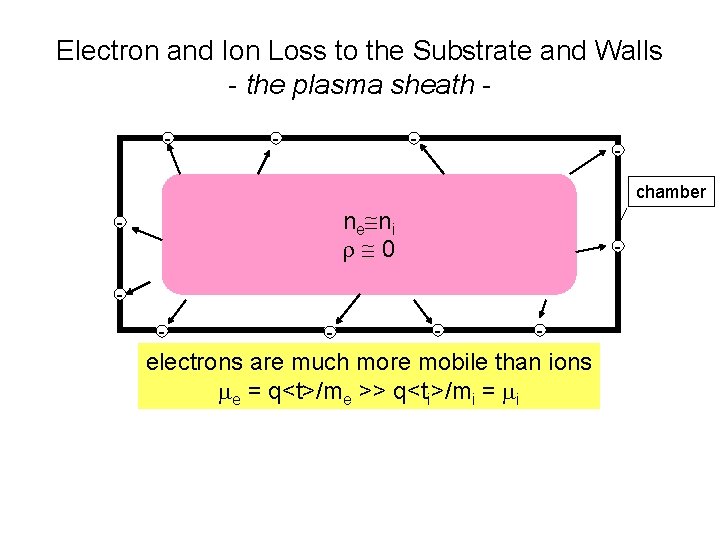
Electron and Ion Loss to the Substrate and Walls - the plasma sheath - - - chamber ne ni r 0 - - - electrons are much more mobile than ions me = q<t>/me >> q<ti>/mi = mi

Electron and Ion Loss to the Substrate and Walls - the plasma sheath s ne<<ni ne = ni (sheath) -1 k. V r(x) + + x V(x) + 0 v V x e x (after Mahan, 2000) low energy electrons are trapped within the plasma, but ions are accelerated by the sheath potential to the chamber walls and substrate

Ion Flux The ion flux to a solid object is determined by the Bohm velocity (or sound speed) of the ion: u. B = (k. Te/mi)1/2 = 9. 8 x 105 (Te/M)1/2 cm/s =9. 8 x 105 (3 e. V/40 amu)1/2 ~ 2. 5 x 105 cm/s …and the ion flux is given by Gi = u. Bni (cm-2 s-1) (this is the ion speed at the edge of the sheath)

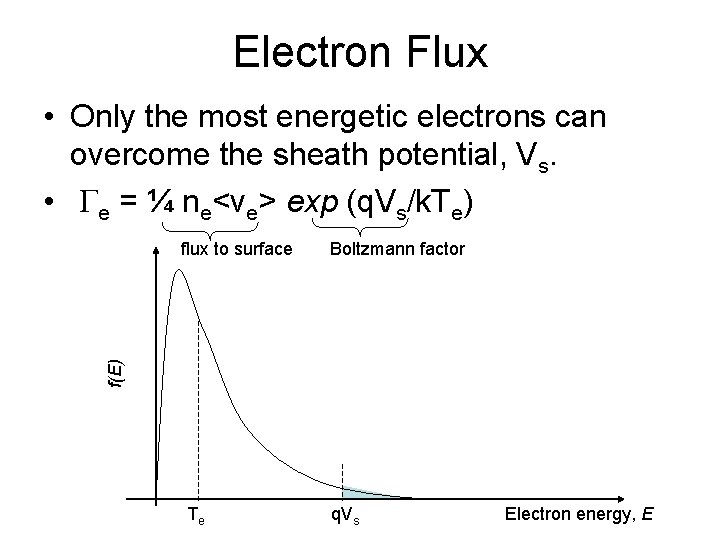
Electron Flux • Only the most energetic electrons can overcome the sheath potential, Vs. • Ge = ¼ ne<ve> exp (q. Vs/k. Te) Boltzmann factor f(E) flux to surface Te q. Vs Electron energy, E

Sheath Potential, Vs In the steady state, the electron and ion fluxes to the chamber/substrate must be equal, if there is no external current path Ge = Gi ¼ ne<ve> exp (q. Vs/k. Te) = u. Bni = (k. Te/mi)1/2 ne giving Vs = -Teln(mi/2 pme) ~ -5 Te This is often called the floating potential: Isolated surfaces have a negative potential relative to the plasma.

Ion Energy Ex: Assuming argon with Te = 3 e. V, s the ion energy at the cathode is Ei = q(1 k. V + 4. 7 Te) = 1014 e. V ignoring ion-neutral collision within s, and the ion energy at the anode is -1 k. V 0 v Ei = 4. 7 Te = 14 e. V V Ion mean free path: x li = 1/ngassi ~ 3/p (cm) for Ar+ …where p is the pressure in m. Torr Here li = 3/100 cm or 0. 3 mm @ 0. 1 torr NOTE: s>>li Ei << 1014 e. V! (after Mahan, 2000)

Particle Conservation and Electron Temperature A simple model for electron temperature can be found for a steady state plasma: # of ions created/sec = # of ions lost/sec Kizngasne. V = u. Bni. Aeff ne=ni Kiz/u. B = Kizoe-E /k. T /(k. Te/mi)1/2 = Aeff/(V ngas) =1/deffngas iz e (V=plasma volume, Aeff = effective chamber area, deff = V/Aeff)

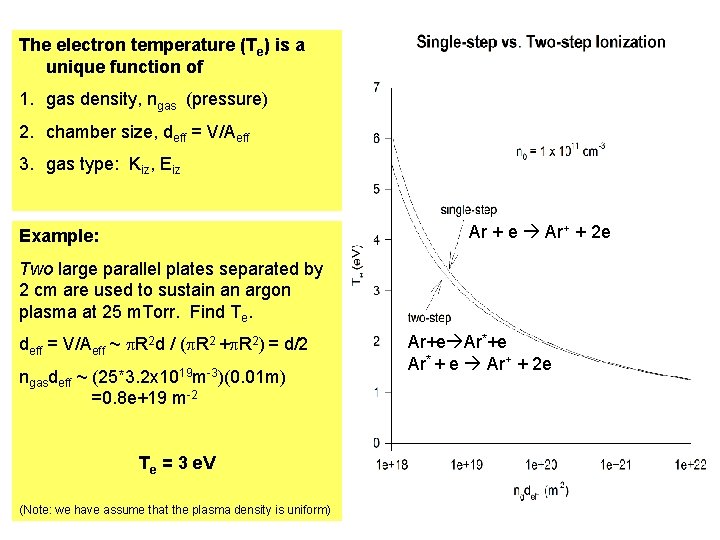
The electron temperature (Te) is a unique function of 1. gas density, ngas (pressure) 2. chamber size, deff = V/Aeff 3. gas type: Kiz, Eiz Ar + e Ar+ + 2 e Example: Two large parallel plates separated by 2 cm are used to sustain an argon plasma at 25 m. Torr. Find Te. deff = V/Aeff ~ p. R 2 d / (p. R 2 +p. R 2) = d/2 ngasdeff ~ (25*3. 2 x 1019 m-3)(0. 01 m) =0. 8 e+19 m-2 Te = 3 e. V (Note: we have assume that the plasma density is uniform) Ar+e Ar* + e Ar+ + 2 e

Power Conservation and Electron Density, ne Power Absorbed by the Plasma = Power Lost from the Plasma Pion Pelectron Pabs = [qniu. BEion+q(¼ne<ve>e. V /k. T )Eelec]Aeff +(Pheat+Plight+Pdiss) ≡ qneu. BAeff(Eion + Eelec + Ec) s q. Vs e 2 Te where EC is the collisional energy lost in creating an electron-ion pair due to ionization, light, dissociative collisions, and heat: EC = [niz. Eiz + nex. Eex + ndiss. Ediss + nm(3 me/mi)Te]/niz

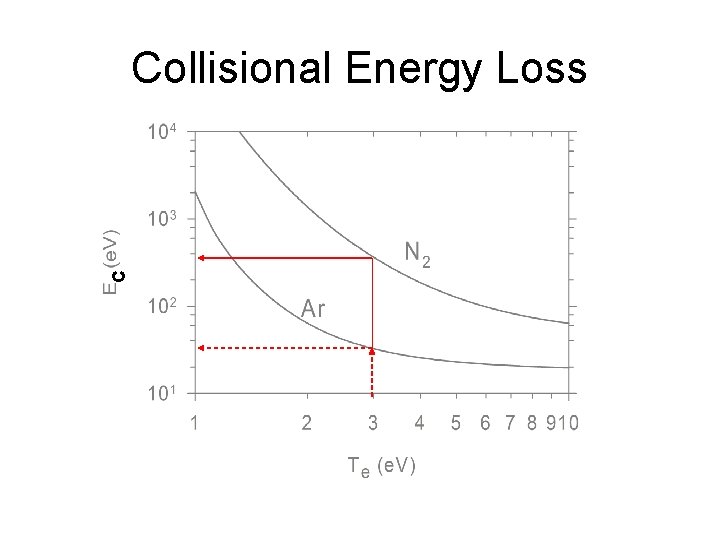
C Collisional Energy Loss

Electron Density Example Continuing with the previous example A plasma is sustained in argon at 25 m. Torr between two parallel plates separated by 2 cm. The radius of the plates is 20 cm and the power absorbed by the plasma is 100 watts. Find ne. 100 W = qneu. BAeff(Eion + Eelec + Ec) = (1. 6 x 10 -19 C)ne(2. 5 x 105 cm/s)(2 px 202 cm 2) x (5 Te + 2 Te + 35 e. V) ne = 1. 3 x 1010 cm-3 Find ne if the gas is N 2, assuming that Te ~ 3 e. V 100 W = (1. 6 x 10 -19 C)ne(2. 5 x 105 cm/s)(2 px 202 cm 2)(5 Te + 2 Te + 400 e. V) ne = 2. 3 x 109 cm-3

Example (cont’d) Repeat the previous example using argon, BUT include an electrode voltage of 1000 v that is applied to one plate to sustain the plasma. 100 W = qneu. BAeff(Eion + Eelec + Ec) = (1. 6 x 10 -19 C)ne(2. 5 x 105 cm/s)(px 202 cm 2) x {(5 Te + 2 Te + 35 e. V)+[(1000 e. V+5 Te) + 2 Te + 35 e. V]} anode cathode ne = 1. 7 x 109 cm-3

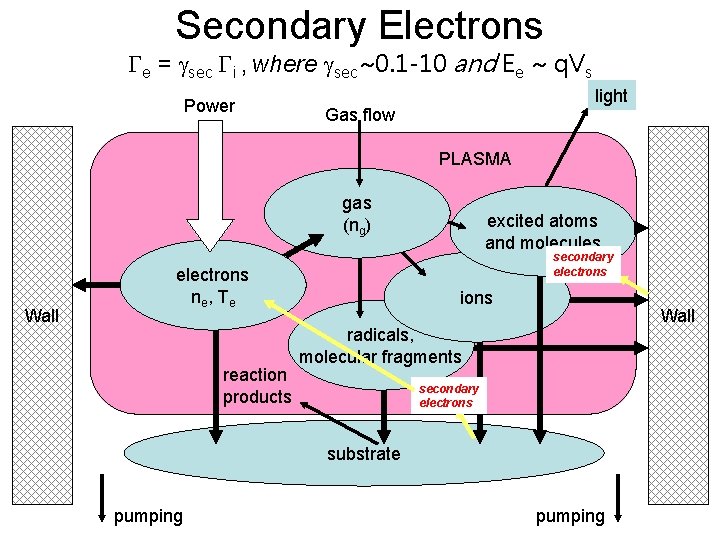
Secondary Electrons Ge = gsec Gi , where gsec~0. 1 -10 and Ee ~ q. Vs Power light Gas flow PLASMA gas (ng) Wall secondary electrons ne , T e reaction products excited atoms and molecules ions Wall radicals, molecular fragments secondary electrons substrate pumping

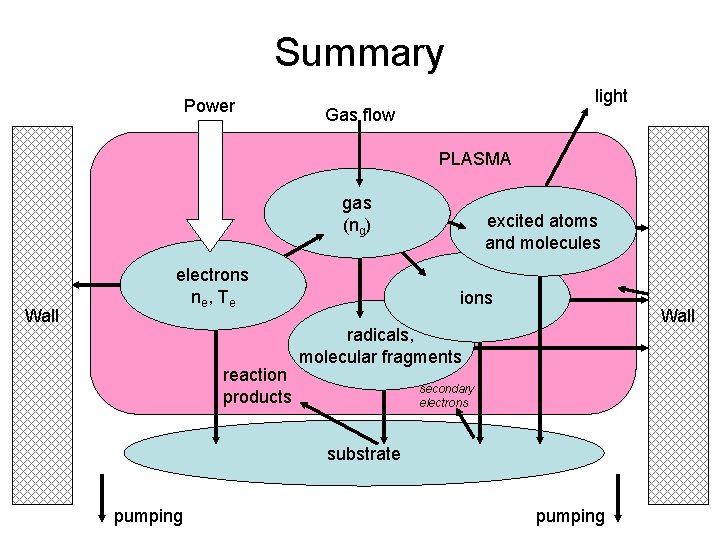
Summary Power light Gas flow PLASMA gas (ng) Wall electrons ne , T e reaction products excited atoms and molecules ions Wall radicals, molecular fragments secondary electrons substrate pumping

Conclusion • Basics of Vacuum – ng, <v>, Gn, , l • Plasma Generation and Simple Models – T e , n i , Gi • Basic Plasma Generation – DC (sputter deposition systems) – AC < 400 k. Hz (plasma displays, lighting) – Radio Frequency 0. 4<f<900 MHz (etching and deposition) – Microwave > 900 MHz