EE148 Expectation Maximization Markus Weber 51199 Overview Expectation

EE-148 Expectation Maximization Markus Weber 5/11/99

Overview • Expectation Maximization is a technique used to estimate probability densities under missing (unobserved) data. – Density Estimation – Observed vs. Missing Data – EM

Probability Density Estimation Why is it important? • It is the essence of – Pattern Recognition estimate p(class|observations) from training data – Learning Theory (includes pattern recognition) • Many other methods use density estimation – HMM – Kalman Filters

Probability Density Estimation how does it work? • Given: samples, {xi} • Two major philosophies: Parametric • Provide a parametrized class of density functions, e. g. Non-Parametric • Density is modeled explicitly through the samples, e. g. – Gaussians: p(x) = f(x, mean, Cov) – Mixture of Gaussians: p(x) = f(x, Mean, Cov, • • Estimation means to find the parameters which best model the data. • • Measure? Maximum Likelihood! Choice of class reflects prior knowledge – Parzen Windows (Rosenblatt, ‘ 56; Parzen, ‘ 62): Make a histogram and convolve with kernel (could be Gaussian) K-nearest-neighbor Prior knowledge less prominent

Maximum Likelihood • The standard method (besides Bayesian inference) for parametric density estimation • Def. Likelihood of a parameter (independent samples): • Oftentimes one uses negative log-likelihood: • We can use this as an error function while estimating . • For a Gaussian, the sample mean and covariance are the ML estimates!

Missing Data Problems • Occur whenever part of the data is unknown – intrinsically inaccessible, e. g. : • Constellation models: p(X, N, d, h, O) d, h not known! p(O|X, N)? • Gaussian mixture models: which cluster does a data point belong to? – data is lost/erroneous e. g. : • Some faulty/noisy process has generated the data. • You erased the wrong file and part of your data is gone. • If the missing data is correlated in any way with the observed, we can hope to extract information about the missing data from the observed. • If the missing data is independent from the observed, everything is lost.
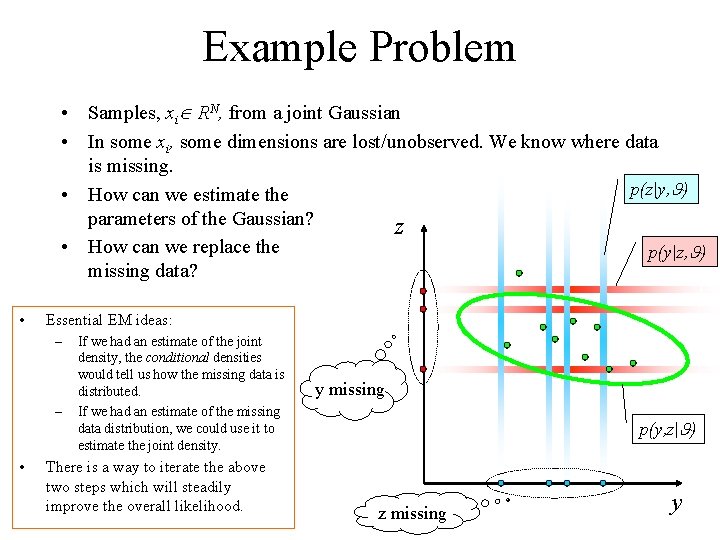
Example Problem • Samples, xi RN, from a joint Gaussian • In some xi, some dimensions are lost/unobserved. We know where data is missing. p(z|y, ) • How can we estimate the parameters of the Gaussian? z • How can we replace the p(y|z, ) missing data? • Essential EM ideas: – – • If we had an estimate of the joint density, the conditional densities would tell us how the missing data is distributed. If we had an estimate of the missing data distribution, we could use it to estimate the joint density. There is a way to iterate the above two steps which will steadily improve the overall likelihood. y missing p(y, z| ) z missing y

Expectation Maximization • Task: Estimate p(y, z| , ) (Gaussian) from the available data. • We want to do maximum likelihood density estimation, although we do not know all the data. If we knew the missing data, we would minimize the negative log-likelihood (o = observed, m = missing): • Since we do not know the missing data, Xm, we want to minimize the likelihood of the observed data, Xo: • We propose an iterative solution ( 1, 2, . . . ) • But for now we are still stuck with a log of an integral.

Some Rewriting • • We write pn(. ) for p(. | n). We can rewrite the expression for the likelihood: and similarly: Now we use Jensen’s inequality: and obtain
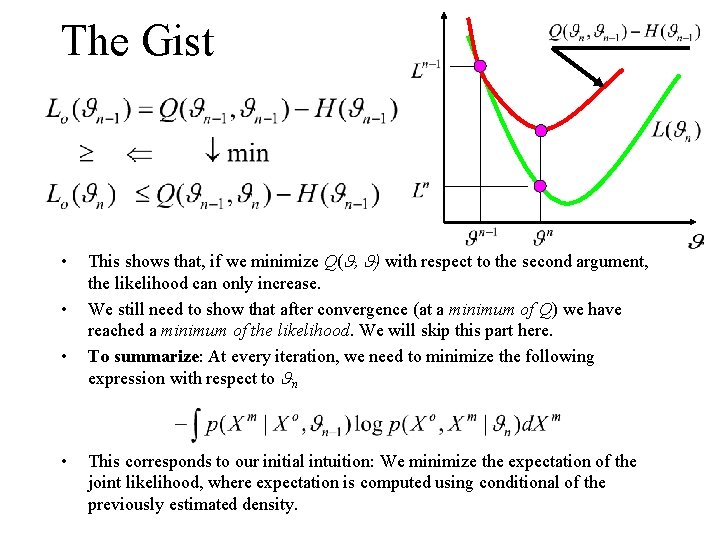
The Gist • • This shows that, if we minimize Q( , ) with respect to the second argument, the likelihood can only increase. We still need to show that after convergence (at a minimum of Q) we have reached a minimum of the likelihood. We will skip this part here. To summarize: At every iteration, we need to minimize the following expression with respect to n This corresponds to our initial intuition: We minimize the expectation of the joint likelihood, where expectation is computed using conditional of the previously estimated density.

Specific Example • This is what we need to minimize: • Concrete: the Gaussian example, z. T = (xo, xm)T: • Update rule for is equally simple to derive.

Solution to Example Problem (for proof see separate handout) • Compute at each iteration:

Demo

Other Applications of EM • Estimating mixture densities • Learning constellation models from unlabeled data • Many problems can be formulated in an EM framework: – – – HMMs PCA Latent variable models “condensation” algorithm (learning complex motions) many computer vision problems
- Slides: 14