EE 562 ARTIFICIAL INTELLIGENCE FOR ENGINEERS Lecture 14

EE 562 ARTIFICIAL INTELLIGENCE FOR ENGINEERS Lecture 14, 5/23/2005 University of Washington, Department of Electrical Engineering Spring 2005 Instructor: Professor Jeff A. Bilmes 5/23/2005 EE 562

Uncertainty Chapter 13 5/23/2005 EE 562

Outline • • • Limitations of logic (Gödel) Uncertainty Probability Syntax and Semantics Inference Independence and Bayes' Rule 5/23/2005 EE 562

Reminder • HW 4 Due Today!! 5/23/2005 EE 562

General Logics • Ontology: – science or study of being, which problems are being investigated, the kinds of abstract entities that are to be admitted to a language system, things that exist in a system. • Epistemology: – study of methods and grounds of knowledge, its limits, and its validity, theories of knowledge. 5/23/2005 EE 562

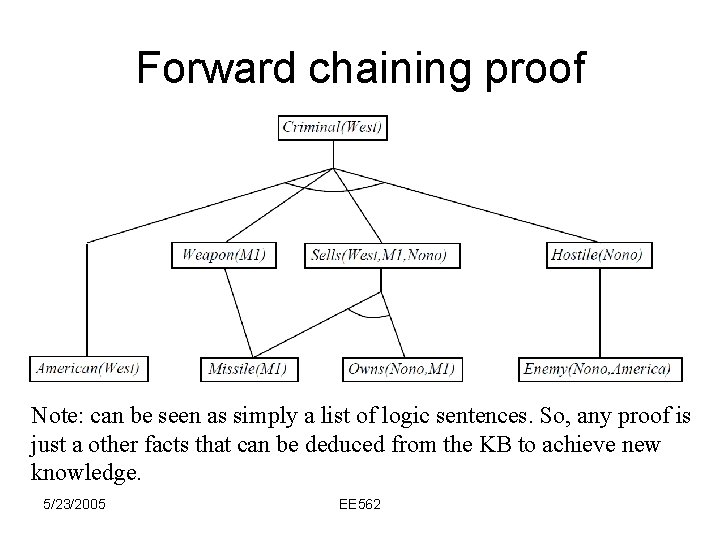
Example knowledge base • The law says that it is a crime for an American to sell weapons to hostile nations. The country Nono, an enemy of America, has some missiles, and all of its missiles were sold to it by Colonel West, who is American. • Prove that Col. West is a criminal 5/23/2005 EE 562

Example knowledge base (in logic form). . . it is a crime for an American to sell weapons to hostile nations: American(x) Weapon(y) Sells(x, y, z) Hostile(z) Criminal(x) Nono … has some missiles, i. e. , x Owns(Nono, x) Missile(x): Owns(Nono, M 1) and Missile(M 1) … all of its missiles were sold to it by Colonel West Missile(x) Owns(Nono, x) Sells(West, x, Nono) Missiles are weapons: Missile(x) Weapon(x) An enemy of America counts as "hostile“: Enemy(x, America) Hostile(x) West, who is American … American(West) The country Nono, an enemy of America … 5/23/2005 Enemy(Nono, America) EE 562

Forward chaining proof Note: can be seen as simply a list of logic sentences. So, any proof is just a other facts that can be deduced from the KB to achieve new knowledge. 5/23/2005 EE 562

Gödels Incompleteness Theorem (general idea) • Each sentence in logic has a length (say number of symbols). • We can enumerate all the sentences in any logic system with a finite number of different types of function symbols (e. g. , 8, 9, +, £, , x, etc. ) • First enumerate all sentences of length 1 (a finite number of them), then number all of length 2 (again, a finite number), etc. • Thus, there a countable number of possible sentences in logic. 5/23/2005 EE 562

Gödels Incompleteness Theorem (general idea) • Let #( ) be the number of sentence • Let #-1(j) be the sentence for number j • Note that all proofs have numbers also. – i. e. , a sequence of sentences also has a number, and any proof can be seen as a sequence of sentences. • Let A be a set of true sentences. 5/23/2005 EE 562

Gödels Incompleteness Theorem (basic idea) • Let A be a set of true premises (e. g. , could be thought of as a KB, i. e. , A=KB) • Consider the following sentence, represented by the function (j, A), – when we use only premises in A, then: • In words: there is no sentence i that proves j, when we start using only A. • This sentence (j, A), like all others, is one that can be either true or false under A. 5/23/2005 EE 562

Gödels Incompleteness Theorem (basic idea) • Repeated: (j, A) is the sentence: – when we use only premises in A, then: • Now consider the sentence defined as: • is the sentence that states its own unprovability when using only A. The sentence , again, can be true or false. • In A, assume true, then it is false 5/23/2005 EE 562 • In A, assume false, then it is true.

Gödels Incompleteness Theorem (basic idea) • Assume follows from A, but then is false (since says it doesn’t follow from A). • But then if is false, then does follow from A, which means A must be false (violating our premise) • Thus is not provable from A, which is what claims, so is true. • Key: is true, but we can’t prove it. • We could always make A bigger, but then same problem would arise in the new A for a new . 5/23/2005 EE 562

General Logics • Ontology: – science or study of being, which problems are being investigated, the kinds of abstract entities that are to be admitted to a language system, things that exist in a system. • Epistemology: – study of methods and grounds of knowledge, its limits, and its validity, theories of knowledge. 5/23/2005 EE 562

Uncertainty • The real world contains uncertainty, we can never be sure of our premises and we can never be sure our outcomes follow our premises. • Instead, we have degrees of belief about the world. Our knowledge ideally reflects degrees of belief in a way that helps us make decisions when uncertainty abounds. 5/23/2005 EE 562

Why we need uncertainty Let action At = leave for airport t minutes before flight Will At get me there on time? Problems: 1. partial observability (road state, other drivers' plans, etc. ) 1. noisy sensors (traffic reports, road conditions) 1. uncertainty in action outcomes (flat tire, etc. ) 1. immense complexity of modeling and predicting traffic Hence a purely logical approach either 1. 2. “A 25 will 5/23/2005 risks falsehood: “A 25 will get me there on time”, or leads to conclusions that are too weak for decision making: get me there on time if there's no accident on the bridge, and it doesn't EE 562 rain, and my tires remain intact, and they aren’t doing construction, etc

Methods for handling uncertainty • Default or nonmonotonic logic: – Assume my car does not have a flat tire – Assume A 25 works unless contradicted by evidence – Key issue: we draw conclusions tentatively, reserving the right to retract a conclusion in light of further information. Set of conclusions entailed by KB does not increase, and might decrease, with size of the KB itself. • Issues: What assumptions are reasonable? How to handle contradiction? • Rules with fudge factors: – A 25 |→ 0. 3 get there on time – Sprinkler |→ 0. 99 Wet. Grass – Wet. Grass |→ 0. 7 Rain • Issues: Problems with combination, e. g. , Sprinkler causes Rain? ? • Probability 5/23/2005 – Model agent's degree of belief EE 562

Probability as Belief Probabilistic assertions summarize effects of – laziness: failure to enumerate exceptions, qualifications, etc. – ignorance: lack of relevant facts, initial conditions, etc. But this presupposes a deterministic world, i. e. , uncertainty exists only from laziness or ignorance. Does randomness truly exist? ? Subjective (Bayesian) probability: • Probabilities relate propositions to agent's own state of knowledge e. g. , P(A 25 | no reported accidents) = 0. 06 These are not assertions about the world, rather agent’s belief. These are NOT claims of a “probabilistic tendency” in current situation (but might be learned from past experience of similar situations) Probabilities of propositions change with new evidence: 5/23/2005 EE 562 e. g. , P(A 25 | no reported accidents, 5 a. m. ) = 0. 15

Making decisions under uncertainty Suppose I believe the following: P(A 25 gets me there on time | …) P(A 90 gets me there on time | …) P(A 120 gets me there on time | …) P(A 1440 gets me there on time | …) = 0. 04 = 0. 70 = 0. 95 = 0. 9999 • Which action to choose? Depends on my preferences for missing flight vs. time spent waiting, etc. 5/23/2005 EE 562 – Utility theory is used to represent and infer preferences

Probability basics • Begin with set , sample space – e. g. , 6 possible rolls of a die – 2 is a sample point, possible world, or atomic event • A probability space (or prob. model) is a sample space with a numeric assignment P( ) for every 2 , s. t. : – 0 · P( ) · 1 – P( ) = 1 • e. g. , P(1)=P(2)=…=P(6) = 1/6 • An event A is any subset of – P(A) = 2 A P( ) • E. g. , P(die roll < 4) = P(1)+P(2)+P(3)+P(4)=3*1/6=1/2 5/23/2005 EE 562

Random Variables • A random variable is a function from sample points to some range, e. g. , the reals or booleans – e. g. , Odd(i) = true, whenever i is odd. • P induces a probability distribution for any r. v. X: – P(X=xi) = : X( ) = xi P( ) • e. g. , in die case, we have that P(Odd = true) = P(1)+P(3)+P(5) = 1/2 5/23/2005 EE 562

Propositions • Think of a proposition as the event (set of basic sample points in ) where the proposition is true. • Given Boolean random variables A and B: – event a = set of sample points where A( ) = true – event : a = set of sample points where A( ) = false – event aÆb = points where both A( ) = true and B( ) = truen • Often in AI applications, sample points are defined by the values of a set of random variables, i. e. , sample space is Cartesian product of r. v. ’s ranges • With boolean variables, sample point = model in propositional logic (i. e. , assignment to prop log vars) – e. g. , A=true, B=true, or aÆ: b • Proposition = disjunction of atomic events that are true – e. g. , (a Ç b) ´ (: a Æ b) Ç (a Æ : b) Ç (a Æ b) – P(a Æ b) = P(: a Æ b) + P(a Æ : b) + P(a Æ b) 5/23/2005 EE 562

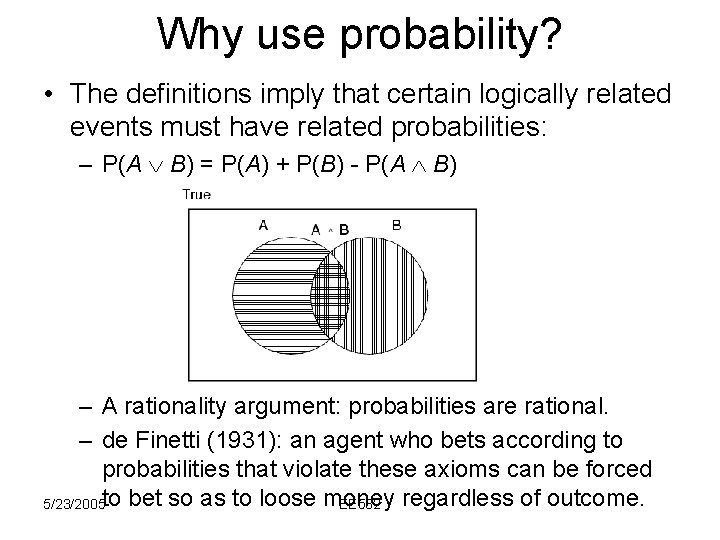
Why use probability? • The definitions imply that certain logically related events must have related probabilities: – P(A B) = P(A) + P(B) - P(A B) – A rationality argument: probabilities are rational. – de Finetti (1931): an agent who bets according to probabilities that violate these axioms can be forced 5/23/2005 to bet so as to loose money EE 562 regardless of outcome.

Syntax for propositions • Propositional or Boolean random variables: – E. g. , Cavity (do I have a cavity? ) – Cavity=true is a proposition, also written just as cavity. • Discrete random variables e. g. , Weather is one of <sunny, rainy, cloudy, snow> Weather=train is a proposition Domain values must be exhaustive and mutually exclusive • Elementary proposition constructed by assignment of a value to a • random variable: e. g. , Weather = sunny, Cavity = false • (abbreviated as cavity) 5/23/2005 EE 562 • Complex propositions formed from elementary propositions and standard logical connectives e. g. , Weather = sunny Cavity = false

Syntax • Atomic event: A complete specification of the state of the world about which the agent is uncertain E. g. , if the world consists of only two Boolean variables Cavity and Toothache, then there are 4 distinct atomic events: Cavity = false Toothache = false Cavity = false Toothache = true Cavity = true Toothache = false Cavity = true Toothache = true EE 562 • Atomic events are mutually exclusive and 5/23/2005

Prior probability • Prior or unconditional probabilities of propositions e. g. , P(Cavity = true) = 0. 1 and P(Weather = sunny) = 0. 72 correspond to belief prior to arrival of any (new) evidence • Probability distribution gives values for all possible assignments: P(Weather) = <0. 72, 0. 1, 0. 08, 0. 1> (normalized, i. e. , sums to 1) • Joint probability distribution for a set of random variables gives the probability of every atomic event on those random variables P(Weather, Cavity) = a 4 × 2 matrix of values: Weather = Cavity = true Cavity = false 5/23/2005 sunny 0. 144 0. 576 rainy 0. 02 0. 08 EE 562 cloudy 0. 016 0. 064 snow 0. 02 0. 08

Conditional probability • Conditional or posterior probabilities e. g. , P(cavity | toothache) = 0. 8 i. e. , given that toothache is all I know (at the moment). This is *NOT* saying that “if toothache, then 80% chance of cavity”. There might be other information that could either increase or decrease this probability that is simultaneously true along with toothache. • (Notation for conditional distributions: P(Cavity | Toothache) = 2 -element vector of 2 -element vectors) • If we know more, e. g. , cavity is also given, then we have P(cavity | toothache, cavity) = 1 Note: the less specific belief (toothache) remains valid after more evidence arrives, but it is not always useful 5/23/2005 EE 562

Conditional probability • Definition of conditional probability: P(a | b) = P(a b) / P(b) if P(b) > 0 • Product rule gives an alternative formulation: P(a b) = P(a | b) P(b) = P(b | a) P(a) • A general version holds for whole distributions, e. g. , P(Weather, Cavity) = P(Weather | Cavity) P(Cavity) • (View as a set of 4 × 2 equations, not matrix mult. , rather “table multiplication”) 5/23/2005 • Chain EE 562 application of product rule: rule is derived by successive

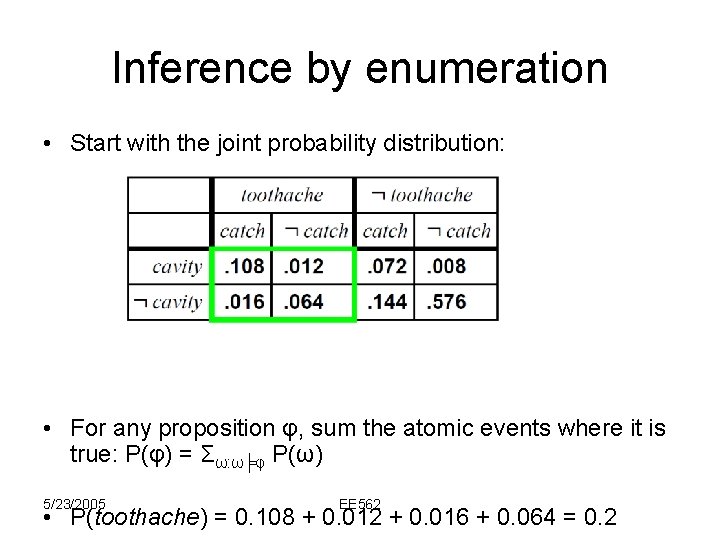
Inference by enumeration • Start with the joint probability distribution: • For any proposition φ, sum the atomic events where it is true: P(φ) = Σω: ω╞φ P(ω) 5/23/2005 EE 562

Inference by enumeration • Start with the joint probability distribution: • For any proposition φ, sum the atomic events where it is true: P(φ) = Σω: ω╞φ P(ω) 5/23/2005 EE 562 • P(toothache) = 0. 108 + 0. 012 + 0. 016 + 0. 064 = 0. 2

Inference by enumeration • Start with the joint probability distribution: • For any proposition φ, sum the atomic events where it is true: P(φ) = Σω: ω╞φ P(ω) 5/23/2005 EE 562 • P(toothache Ç cavity) = 0. 108 + 0. 012 + 0. 016 + 0. 064 =

Inference by enumeration • Start with the joint probability distribution: • Can also compute conditional probabilities: P( cavity | toothache) 5/23/2005 = P( cavity toothache) P(toothache) = 0. 016+0. 064 0. 108 + 0. 012 + 0. 016 + 0. 064 =EE 562 0. 4

Normalization • Denominator can be viewed as a normalization constant α P(Cavity | toothache) = α, P(Cavity, toothache) = α, [P(Cavity, toothache, catch) + P(Cavity, toothache, catch)] = α, [<0. 108, 0. 016> + <0. 012, 0. 064>] = α, <0. 12, 0. 08> = <0. 6, 0. 4> General idea: compute distribution on query variable by fixing evidence variables and summing over hidden variables 5/23/2005 EE 562

Inference by enumeration, contd. Let X be all the variables. Typically, we are interested in the posterior joint distribution of the query variables Y given specific values e for the evidence variables E Let the hidden variables be H = X - Y - E Then the required summation of joint entries is done by summing out the hidden variables: P(Y | E = e) = αP(Y, E = e) = αΣh. P(Y, E= e, H = h) • The terms in the summation are joint entries because Y, E and H together exhaust the set of random variables • Obvious problems: 5/23/2005 EE 562 1. Worst-case time complexity O(dn) where d is the largest arity

Independence • A and B are independent iff P(A|B) = P(A) or P(B|A) = P(B) or P(A, B) = P(A) P(B) P(Toothache, Catch, Cavity, Weather) = P(Toothache, Catch, Cavity) P(Weather) • 16 entries reduced to 10; for n independent biased coins, O(2 n) →O(n) • Absolute independence powerful but rare • Dentistry is a large field with hundreds of variables, none of which 5/23/2005 are independent. What to do? EE 562

Conditional independence • P(Toothache, Cavity, Catch) has 23 – 1 = 7 independent entries • If I have a cavity, the probability that the probe catches in it doesn't depend on whether I have a toothache: (1) P(catch | toothache, cavity) = P(catch | cavity) • The same independence holds if I haven't got a cavity: (2) P(catch | toothache, cavity) = P(catch | cavity) • Catch is conditionally independent of Toothache given Cavity: P(Catch | Toothache, Cavity) = P(Catch | Cavity) 5/23/2005 • Equivalent statements: EE 562

Conditional independence contd. • Write out full joint distribution using chain rule: P(Toothache, Catch, Cavity) = P(Toothache | Catch, Cavity) P(Catch | Cavity) P(Cavity) = P(Toothache | Cavity) P(Catch | Cavity) P(Cavity) I. e. , 2 + 1 = 5 independent numbers • In most cases, the use of conditional independence reduces the size of the representation of the joint distribution from exponential in n to linear in n. 5/23/2005 EE 562

Bayes' Rule • Product rule P(a b) = P(a | b) P(b) = P(b | a) P(a) Bayes' rule: P(a | b) = P(b | a) P(a) / P(b) • or in distribution form P(Y|X) = P(X|Y) P(Y) / P(X) = αP(X|Y) P(Y) • Useful for assessing diagnostic probability from causal probability: – P(Cause|Effect) = P(Effect|Cause) P(Cause) / P(Effect) 5/23/2005 EE 562 – E. g. , let M be meningitis, S be stiff neck:

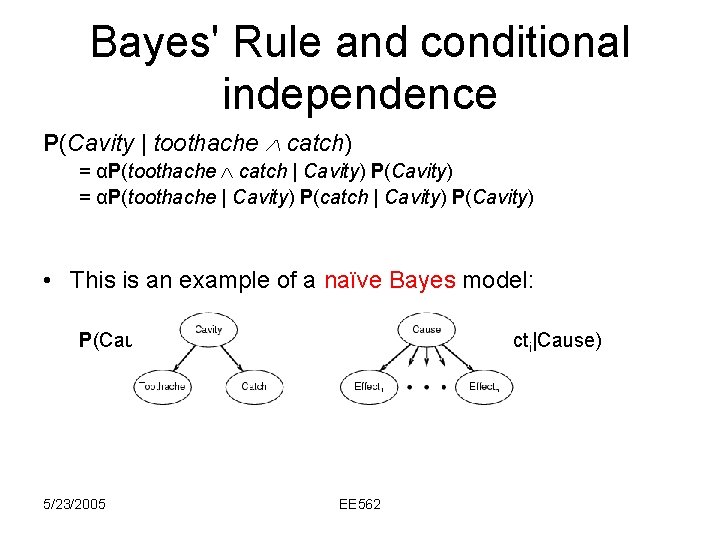
Bayes' Rule and conditional independence P(Cavity | toothache catch) = αP(toothache catch | Cavity) P(Cavity) = αP(toothache | Cavity) P(catch | Cavity) P(Cavity) • This is an example of a naïve Bayes model: P(Cause, Effect 1, … , Effectn) = P(Cause) πi. P(Effecti|Cause) 5/23/2005 EE 562

Key Benefit • Probabilistic reasoning (using things like conditional probability, conditional independence, and Bayes’ rule) make it possible to make reasonable decisions amongst a set of actions, that otherwise (without probability, as in propositional or first order logic) we would have to resort to random guessing. • Example: Wumpus World 5/23/2005 EE 562

Summary • Probability is a rigorous formalism for uncertain knowledge • Joint probability distribution specifies probability of every atomic event • Queries can be answered by summing over atomic events • For nontrivial domains, we must find a way to reduce the joint size 5/23/2005 EE 562 • Independence and conditional independence