EE 53407340 Introduction to Biomedical Engineering Ultrasound Flowprobes

EE 5340/7340 Introduction to Biomedical Engineering Ultrasound Flowprobes Carlos E. Davila, Electrical Engineering Dept. Southern Methodist University slides can be viewed at: http: // www. seas. smu. edu/~cd/ee 5340. html EE 5340/7340, SMU Electrical Engineering Department, © Carlos Davila 1

Ultrasound-Based Flow Measurement n n n Basic Ultrasound Transducer Principles Ultrasound Attennuation, Transmission, and Backscatter Transit Time Flowprobes Doppler Flowprobes Pulsed Doppler EE 5340/7340, SMU Electrical Engineering Department, © Carlos Davila 2

Definition of Ultrasound n n n Sound consists of traveling pressure waves Speed of sound waves is about 1500 m/s in tissue Frequency range: 2 MHz < f < 10 MHz Ultrasound is produced using piezo-electric transducers Applications of Medical Ultrasound n Imaging n Measurement of Blood Flow (Doppler and transittime flowmeters) n Lythotripsy EE 5340/7340, SMU Electrical Engineering Department, © Carlos Davila 3
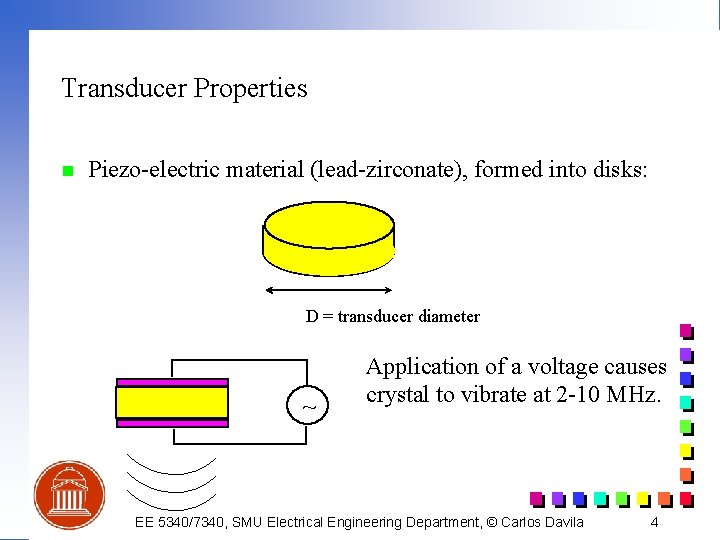
Transducer Properties n Piezo-electric material (lead-zirconate), formed into disks: D = transducer diameter ~ Application of a voltage causes crystal to vibrate at 2 -10 MHz. EE 5340/7340, SMU Electrical Engineering Department, © Carlos Davila 4
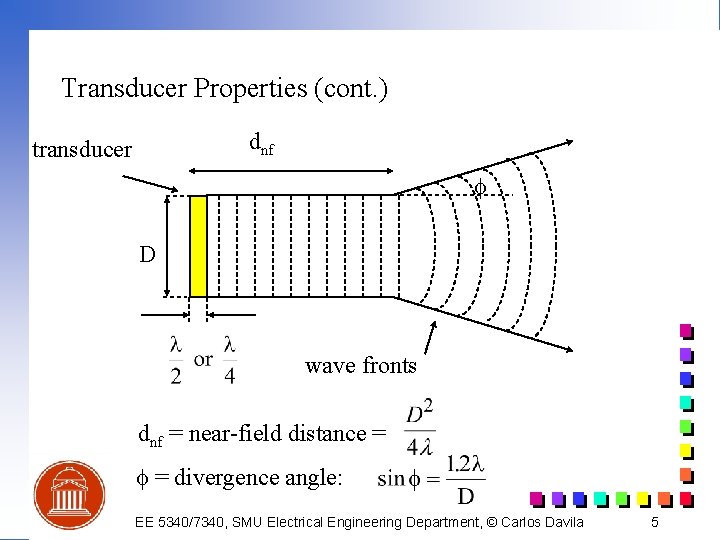
Transducer Properties (cont. ) dnf transducer f D wave fronts dnf = near-field distance = f = divergence angle: EE 5340/7340, SMU Electrical Engineering Department, © Carlos Davila 5

Transducer Properties (cont. ) ~ E = Acos(2 pf t) c=fl n n n crystal will vibrate at same frequency, f, as that of the applied voltage. c: speed of sound in tissue: about 1500 m/s l: wavelength of sound EE 5340/7340, SMU Electrical Engineering Department, © Carlos Davila 6

Transducer Properties (cont. ) n S = change in crystal thickness/original crystal thickness = g. E E: applied electric field g: constant EE 5340/7340, SMU Electrical Engineering Department, © Carlos Davila 7

Transducer Properties (cont. ) n n n If crystal undergoes mechanical compression, a voltage is generated proportional to the compression. In flowmetry, the piezoelectric crystal is used to generate ultrasound, which is transmitted into the tissue. Some of the ultrasound is reflected by the tissue. Voltage is turned off and the crystal is then used to convert the reflected pressure waves to a voltage. The information in the reflected pressure waves can be used to image tissue. EE 5340/7340, SMU Electrical Engineering Department, © Carlos Davila 8

Ultrasound Attennuation in Tissue due to: n n Divergence of wavefronts in the far-field. Conversion of wave energy to heat (exponential with distance): p(z): sound pressure at distance z from transducer face n a: attenuation coefficient n p 0: sound pressure at transducer face n EE 5340/7340, SMU Electrical Engineering Department, © Carlos Davila 9

Attenuation Coefficients at 1 MHz source: Medical Imaging Systems, A. Macovsky, Prentice Hall EE 5340/7340, SMU Electrical Engineering Department, © Carlos Davila 10

Ultrasound Attenuation in Tissue: Rayleigh Scattering n Rayleigh scattering: in red blood cells or other small structures whose diameter is smaller than ultrasound wavelength, will get scattering in all directions. Attenuation (scattering) is proportional to 1/l 4. High frequency ultrasound has greater attenuation than low frequency. In light, Rayleigh scattering explains why the sky is blue. EE 5340/7340, SMU Electrical Engineering Department, © Carlos Davila 11

Ultrasound Attenuation in Tissue: Specular Reflection n Specular reflection at planar interfaces: n tissue characterized by acoustic impedance Z. r: density n c: speed of sound in tissue n sound waves encountering tissue boundary having different acoustic impedances is partially reflected at the interface. n EE 5340/7340, SMU Electrical Engineering Department, © Carlos Davila 12
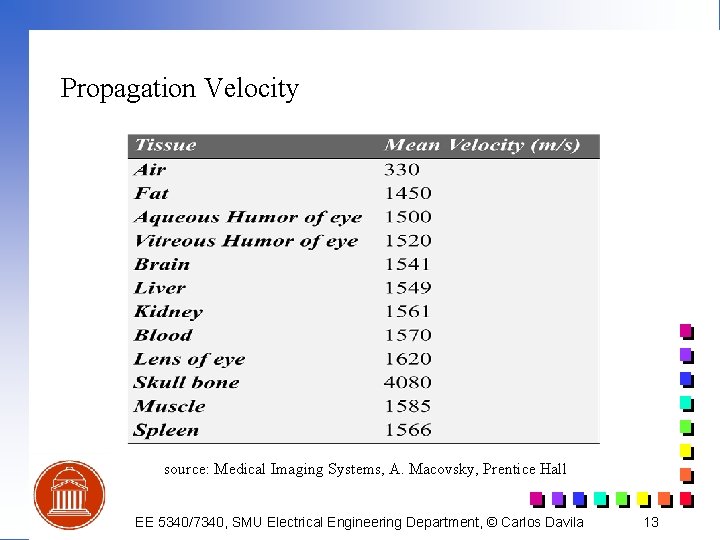
Propagation Velocity source: Medical Imaging Systems, A. Macovsky, Prentice Hall EE 5340/7340, SMU Electrical Engineering Department, © Carlos Davila 13

Models for Ultrasounic Backscatter (Reflection) n Specular reflection: incident z transmitted reflected Z 1 Z 2 tissue interface EE 5340/7340, SMU Electrical Engineering Department, © Carlos Davila 14

Specular Reflection (cont. ) R: reflectivity = source: Medical Imaging Systems, A. Macovsky, Prentice Hall EE 5340/7340, SMU Electrical Engineering Department, © Carlos Davila 15

Models for Ultrasonic Backscatter (cont. ) n Isotropic scattering 1 -D model assumptions: transmitted ultrasound assumed to consist of planar waves (no diffraction). n sound propagates with uniform velocity c. n attennuation coefficient a is uniform throught body. n body is modeled as an array of isotropic (invariant with respect to direction) scatterers. n EE 5340/7340, SMU Electrical Engineering Department, © Carlos Davila 16

Isotropic scattering 1 -D model (cont. ): n Reflected ultrasound has convolution property: : reflected ultrasound pressure wave : transmitted ultrasound pressure wave : reflectivity profile : attennuation due to heat loss : attennuation due to reflected wave divergence (diffraction spreading) EE 5340/7340, SMU Electrical Engineering Department, © Carlos Davila 17

Comparison of Backscatter Models n Note that if Z(z) is a step function, Z 1 h(z) is an impulse function and corresponds to specular reflection. Z 2 n n z Isotropic scattering model is more general, it considers gradual changes in reflectivity. Attennuation is compensated for by electronics. EE 5340/7340, SMU Electrical Engineering Department, © Carlos Davila 18
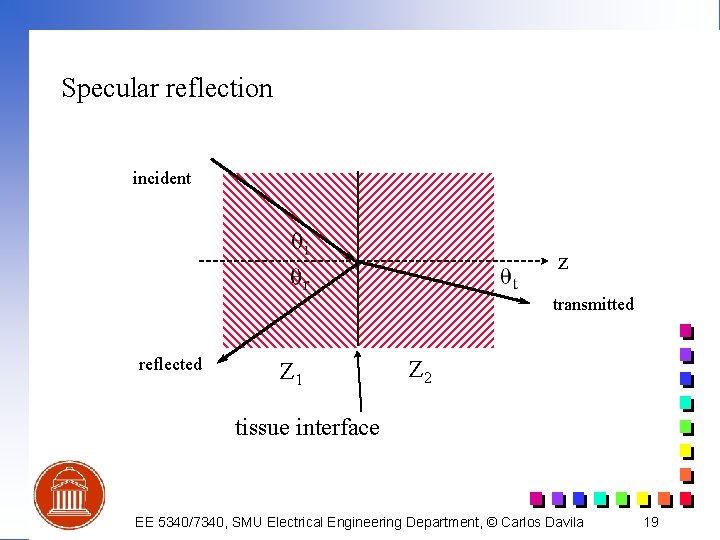
Specular reflection incident z transmitted reflected Z 1 Z 2 tissue interface EE 5340/7340, SMU Electrical Engineering Department, © Carlos Davila 19

Wave Equation (1) p: pressure, f(x, t) x: spatial variable t: time variable K: compressibility of medium along which wave is traveling EE 5340/7340, SMU Electrical Engineering Department, © Carlos Davila 20

Wave Equation Solutions trivial solutions: p = 0 and p = constant these can be verified by substituting into (1). Another solution: (2) A: wave amplitude W: angular frequency of wave k: propagation constant > 0 EE 5340/7340, SMU Electrical Engineering Department, © Carlos Davila 21

Dispersion Equation (2) is a solution to (1) provided that: (3) is satisfied. Equation (3) is called the dispersion equation. Other possible solutions: In fact, any function having the form is a solution provided (3) is satisfied. EE 5340/7340, SMU Electrical Engineering Department, © Carlos Davila 22
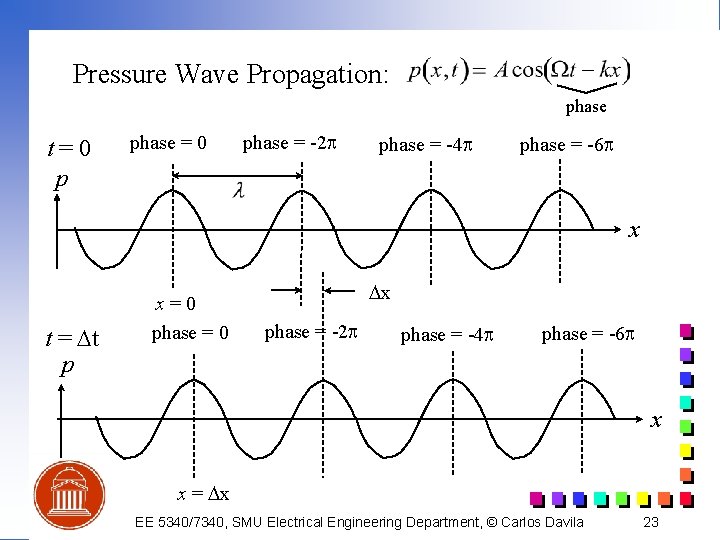
Pressure Wave Propagation: phase t=0 p phase = 0 phase = -2 p phase = -4 p phase = -6 p x t = Dt p x=0 phase = 0 Dx phase = -2 p phase = -4 p phase = -6 p x x = Dx EE 5340/7340, SMU Electrical Engineering Department, © Carlos Davila 23

Wavelength and Phase Velocity wavelength, distance between two successive phase fronts: or (4) phase at t = Dt and x = Dx : (5) EE 5340/7340, SMU Electrical Engineering Department, © Carlos Davila 24
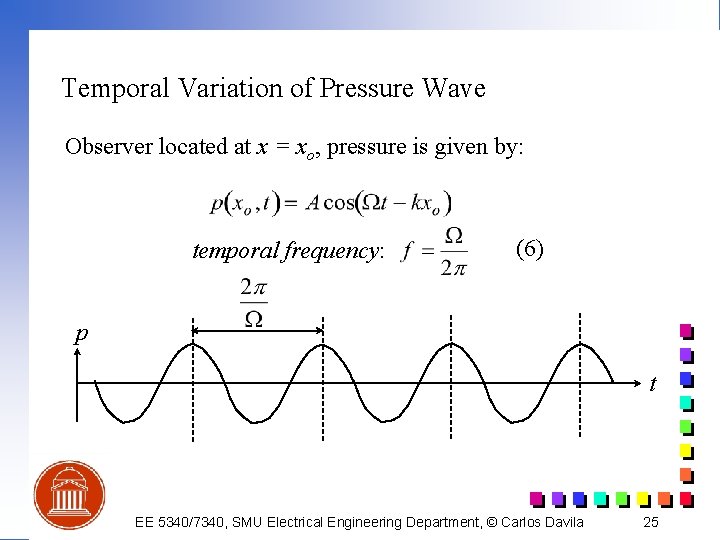
Temporal Variation of Pressure Wave Observer located at x = xo, pressure is given by: temporal frequency: (6) p t EE 5340/7340, SMU Electrical Engineering Department, © Carlos Davila 25

Frequency, Wavelength, and Phase Velocity combining (4), (5), and (6): dispersion equation, (3), can be expressed as: using (5): (7) EE 5340/7340, SMU Electrical Engineering Department, © Carlos Davila 26

Phase Velocity of Sound in Water compressibility, density, from (7): we have looked at 1 -D waves, if wave amplitude is constant along 2 spatial dimensions (x and y), then waves are called plane waves. EE 5340/7340, SMU Electrical Engineering Department, © Carlos Davila 27

Doppler Ultrasound Flowprobes n n n Sound is transmitted “downstream” at frequency ft using an ultrasound transducer-transmitter. Sound strikes red blood cell (RBC) and is reflected (specular reflection), travels “upstream” against blood flow current and strikes the transducer which has been put in receive mode. frequency of reflected ultrasound, fr, has undergone a Doppler shift: proportional to velocity of RBC reflector EE 5340/7340, SMU Electrical Engineering Department, © Carlos Davila 28
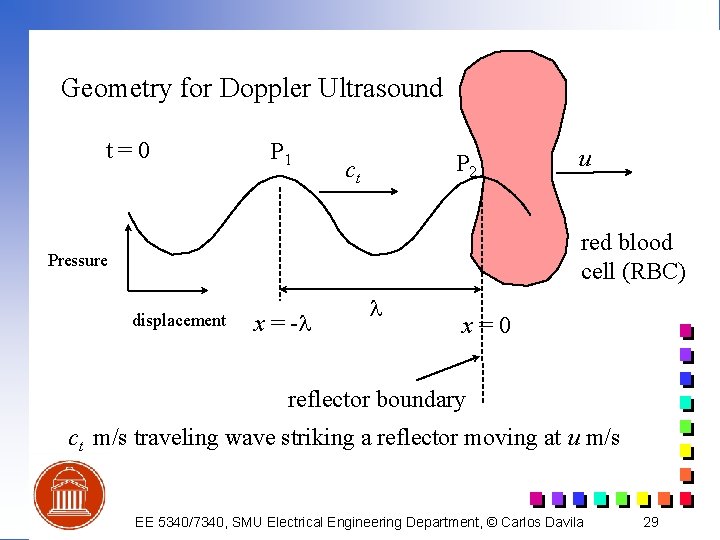
Geometry for Doppler Ultrasound t=0 P 1 P 2 ct u red blood cell (RBC) Pressure displacement x = -l l x=0 reflector boundary ct m/s traveling wave striking a reflector moving at u m/s EE 5340/7340, SMU Electrical Engineering Department, © Carlos Davila 29

Geometry for Doppler Ultrasound (cont. ) n n n P 2 and P 1: successive peaks of ultrasound wave, P 2 strikes reflector at time t = 0. u: velocity of reflector (red blood cell), same direction as sound direction. T: time between peak P 1 and P 2 striking the RBC. ft , l t , ct: frequency, wavelength, and velocity of transmitted ultrasound, ct = c + u fr , l r , cr: frequency, wavelength, and velocity of reflected ultrasound, cr = c - u c: velocity of sound in stationary medium. (8) (9) EE 5340/7340, SMU Electrical Engineering Department, © Carlos Davila 30

First Frequency Shift displacement equation: Dx: displacement, since t = 0 x 0: displacement at t = 0 v: velocity T found by solving: P 1 displacement starting at t = 0 = RBC displacement or (10) EE 5340/7340, SMU Electrical Engineering Department, © Carlos Davila 31

First Frequency Shift (cont. ) frequency of ultrasound if a listener were at the RBC = 1/T Hz or But ultrasound detector is stationary and is located upstream from RBC so frequency of reflected ultrasound (fr) at detector is different from fm. Note also that fm < ft. EE 5340/7340, SMU Electrical Engineering Department, © Carlos Davila 32

Second Frequency Shift wavelength of reflected ultrasound: (11) this requires some thought, imagine moving in a vehicle at u m/s, facing the rear of the vehicle, and throwing a ball once every T seconds at a velocity of cr m/s (w. r. t. a stationary object). Distance between successive balls is lr: cr cr u lr EE 5340/7340, SMU Electrical Engineering Department, © Carlos Davila 33

Second Frequency Shift (cont. ) from (9): substitute (11): subst. (10) for T: subst. for lt using(8): use ct = c + u, cr = c - u: (12) EE 5340/7340, SMU Electrical Engineering Department, © Carlos Davila 34

Total Doppler Frequency Shift Assume c >> u: (13) EE 5340/7340, SMU Electrical Engineering Department, © Carlos Davila 35
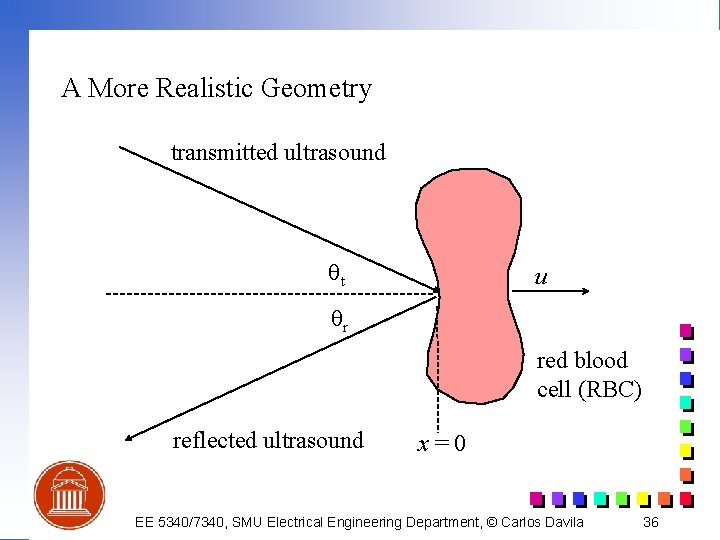
A More Realistic Geometry transmitted ultrasound qt u qr red blood cell (RBC) reflected ultrasound x=0 EE 5340/7340, SMU Electrical Engineering Department, © Carlos Davila 36

A More Realistic Geometry (cont. ) (12) becomes: (13) becomes: (see HW problems) EE 5340/7340, SMU Electrical Engineering Department, © Carlos Davila 37
- Slides: 37