EE 4271 VLSI Design Interconnect Optimizations Buffer Insertion

Moore’s law Twice the number of transistors, approximately every two years, so double clock frequency accordingly

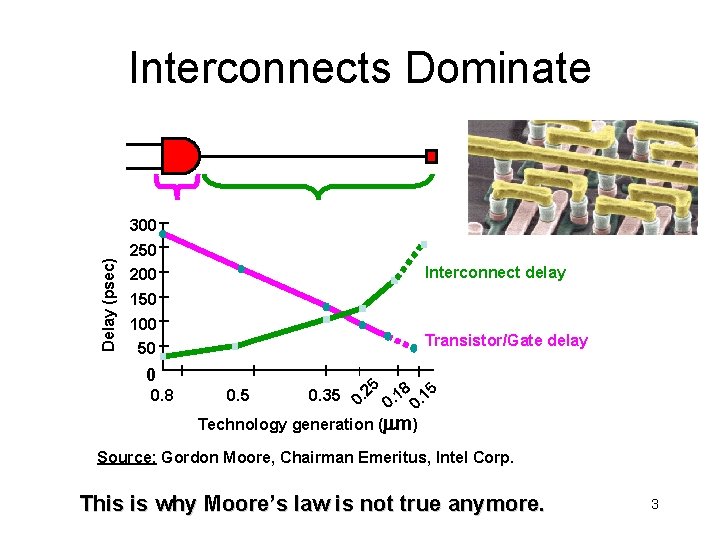
Interconnects Dominate Delay (psec) 300 250 Interconnect delay 200 150 100 Transistor/Gate delay 50 0 0. 8 25. 18. 15. 0. 35 0. 25 0 0 0 Technology generation ( m) 0. 5 Source: Gordon Moore, Chairman Emeritus, Intel Corp. This is why Moore’s law is not true anymore. 3

Objectives • What have we learned? – Compute circuit delay on wires and gates – Gate delay optimization • What are we going to learn? – Interconnect delay optimization: buffer insertion • Why reducing delay • How to perform it – This is the most important optimization in circuit design

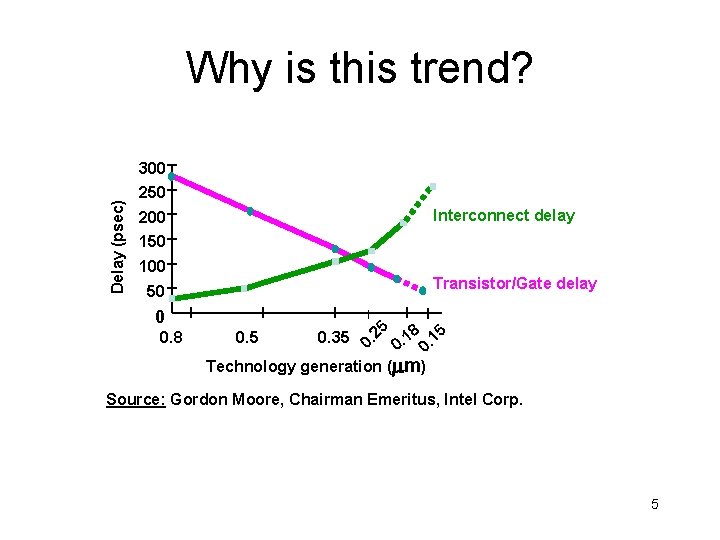
Why is this trend? Delay (psec) 300 250 Interconnect delay 200 150 100 Transistor/Gate delay 50 0 0. 8 25. 18. 15. 0. 35 0. 25 0 0 0 Technology generation ( m) 0. 5 Source: Gordon Moore, Chairman Emeritus, Intel Corp. 5

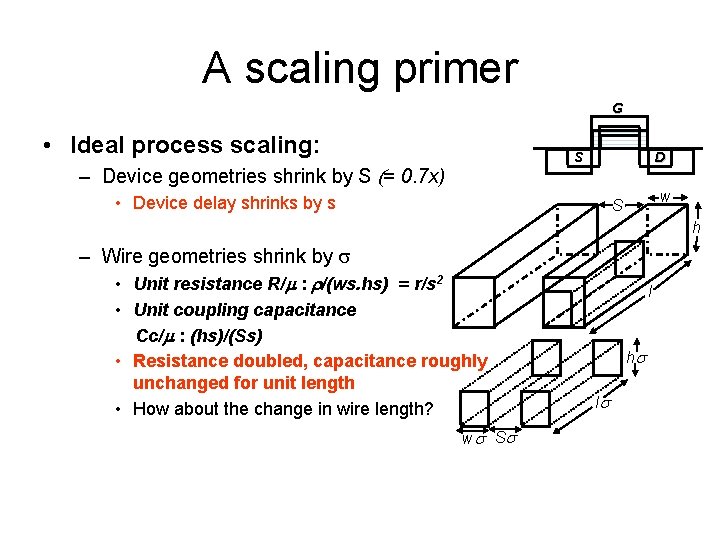
A scaling primer G • Ideal process scaling: S – Device geometries shrink by S (= 0. 7 x) D • Device delay shrinks by s w S h – Wire geometries shrink by s • Unit resistance R/m : r/(ws. hs) = r/s 2 • Unit coupling capacitance Cc/m : (hs)/(Ss) • Resistance doubled, capacitance roughly unchanged for unit length • How about the change in wire length? ws S s l hs ls

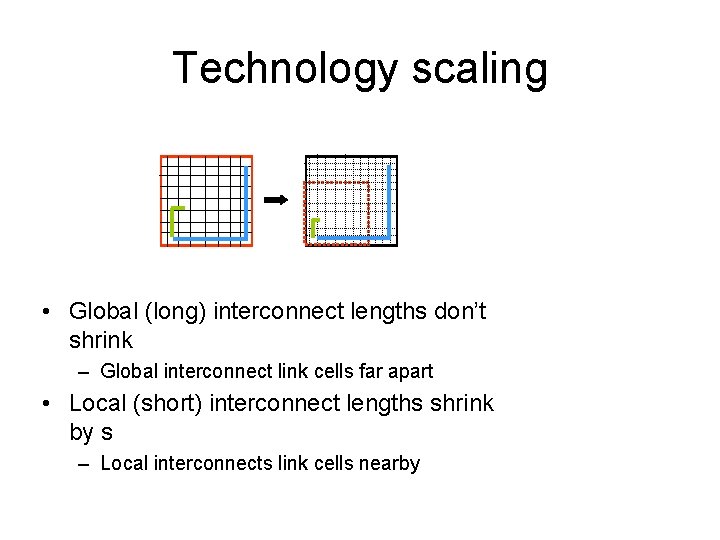
Technology scaling • Global (long) interconnect lengths don’t shrink – Global interconnect link cells far apart • Local (short) interconnect lengths shrink by s – Local interconnects link cells nearby

Interconnect delay scaling • Delay of a wire of length l : tint = (rl)(cl) = rcl 2 (a quadratic function of length) • Local interconnects : tint : (r/s 2)(c)(ls)2 = rcl 2 – Local interconnect delay unchanged • Global interconnects : tint : (r/s 2)(c)(l)2 = (rcl 2)/s 2 – Global interconnect delay doubled – unsustainable! • Interconnect delay increasingly more dominant

Buffer Insertion For Delay Reduction

Elmore Delay for Wire unit wire capacitance c x unit wire resistance r C

Elmore Delay for Buffer u v C Input capacitance Driving resistance

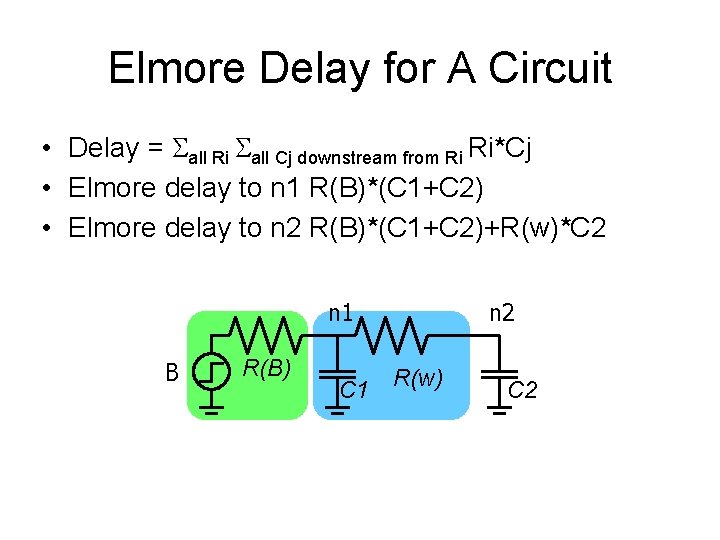
Elmore Delay for A Circuit • Delay = all Ri all Cj downstream from Ri Ri*Cj • Elmore delay to n 1 R(B)*(C 1+C 2) • Elmore delay to n 2 R(B)*(C 1+C 2)+R(w)*C 2 n 1 B R(B) C 1 R(w) n 2 C 2

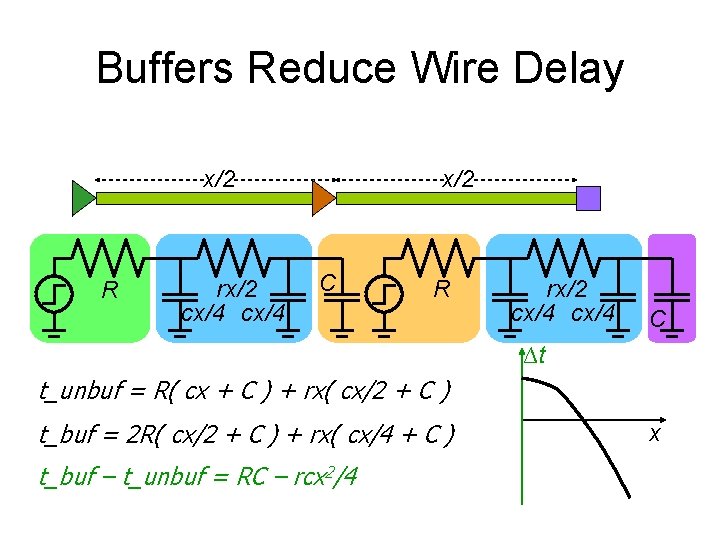
Buffers Reduce Wire Delay x/2 R rx/2 cx/4 x/2 C R rx/2 cx/4 C ∆t t_unbuf = R( cx + C ) + rx( cx/2 + C ) t_buf = 2 R( cx/2 + C ) + rx( cx/4 + C ) t_buf – t_unbuf = RC – rcx 2/4 x

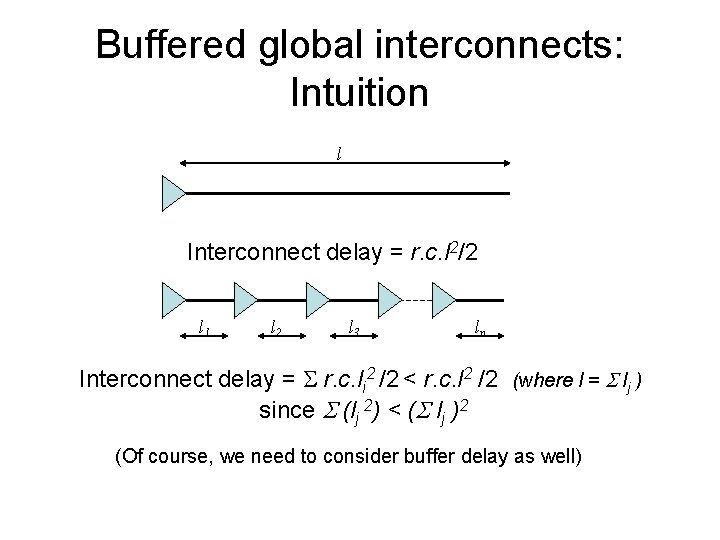
Buffered global interconnects: Intuition l Interconnect delay = r. c. l 2/2 l 1 l 2 l 3 ln Interconnect delay = r. c. li 2 /2 < r. c. l 2 /2 (where l = S lj ) since S (lj 2) < (S lj )2 (Of course, we need to consider buffer delay as well)

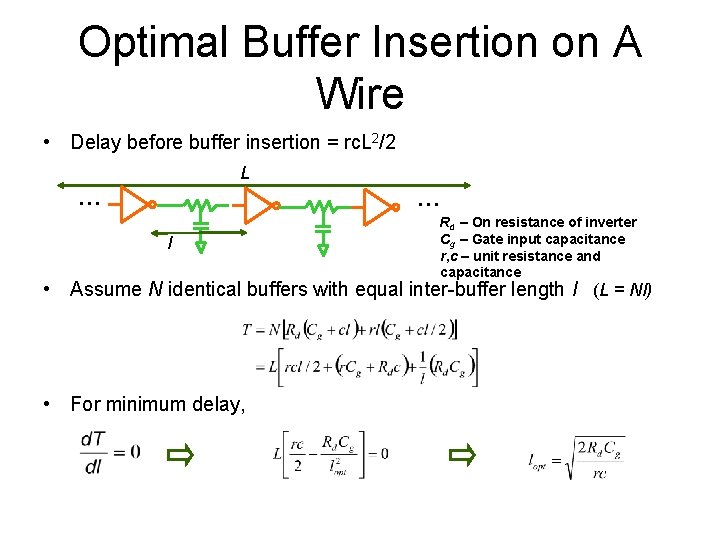
Optimal Buffer Insertion on A Wire • Delay before buffer insertion = rc. L 2/2 L … … l Rd – On resistance of inverter Cg – Gate input capacitance r, c – unit resistance and capacitance • Assume N identical buffers with equal inter-buffer length l (L = Nl) • For minimum delay,

Optimal interconnect delay • Substituting lopt back into the interconnect delay expression: Delay grows linearly with L (instead of quadratically)

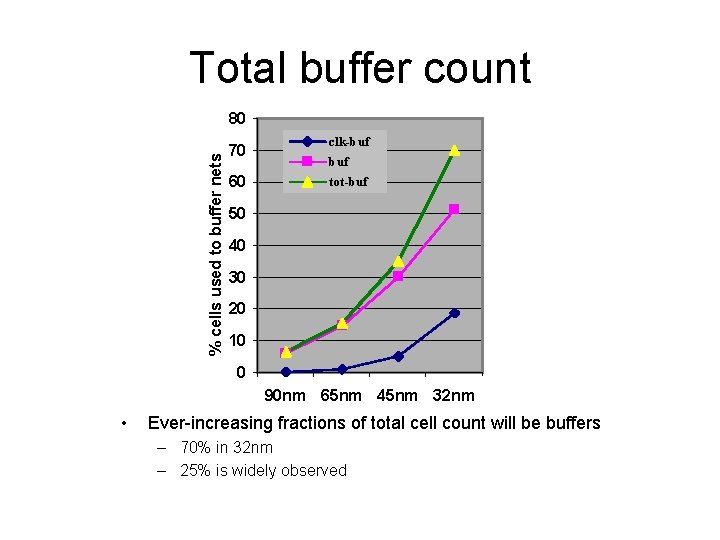
Total buffer count % cells used to buffer nets 80 70 60 clk-buf tot-buf 50 40 30 20 10 0 90 nm 65 nm 45 nm 32 nm • Ever-increasing fractions of total cell count will be buffers – 70% in 32 nm – 25% is widely observed

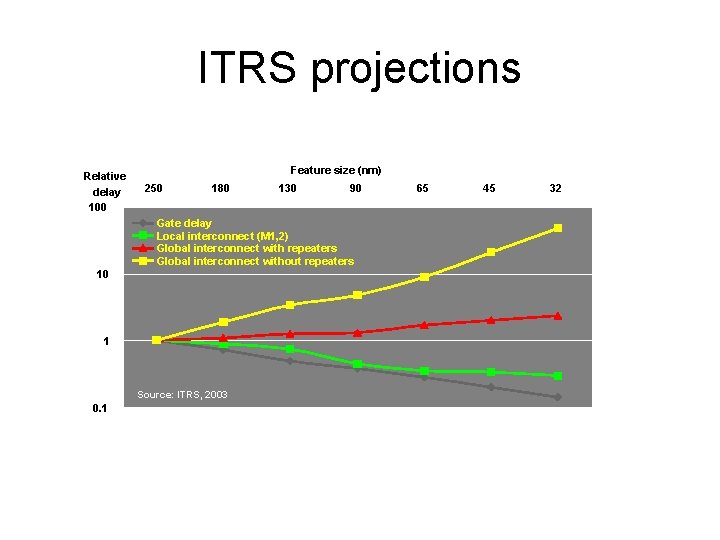
ITRS projections Relative delay 100 Feature size (nm) 250 180 130 90 Gate delay Local interconnect (M 1, 2) Global interconnect with repeaters Global interconnect without repeaters 10 1 Source: ITRS, 2003 0. 1 65 45 32

Exercise 1 • Given a wire of length 10 with r=2, c=2, what is its delay? • Given a buffer with Rd =10, Cg=20, after optimally buffering the wire, what is the delay? • What if wire length is 100? • Any conclusion?

Exercise 2 • Relationship with gate sizing – If we can size the buffer, what is the best buffer size? – Let R 0 denote the unit size buffer driving resistance, and C 0 denote the unit size buffer input capacitance. Thus, Rd=R 0/h and Cg=C 0 h – What is best h leading to smallest delay?

Analogy

Analogy • Advancing technology = period of city expansion, more transistors = larger city • Interconnects = streets • Buffers = gas stations • Signal delay (timing) = time to cross the city • Buffer insertion = gas station construction

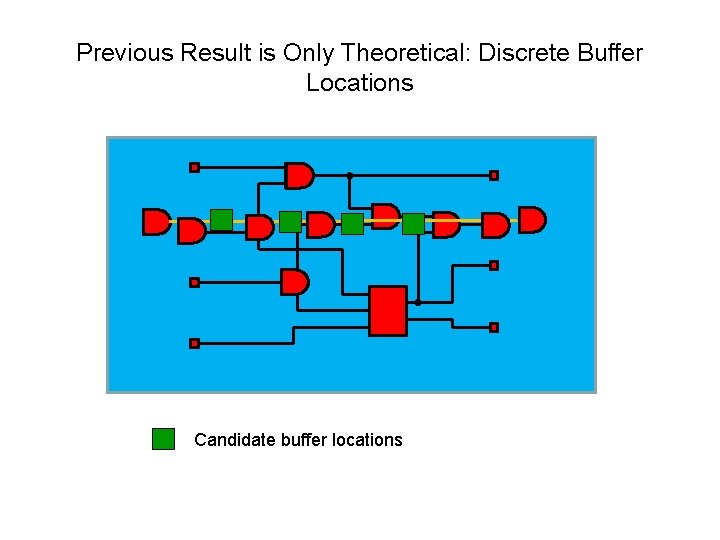
Previous Result is Only Theoretical: Discrete Buffer Locations Candidate buffer locations

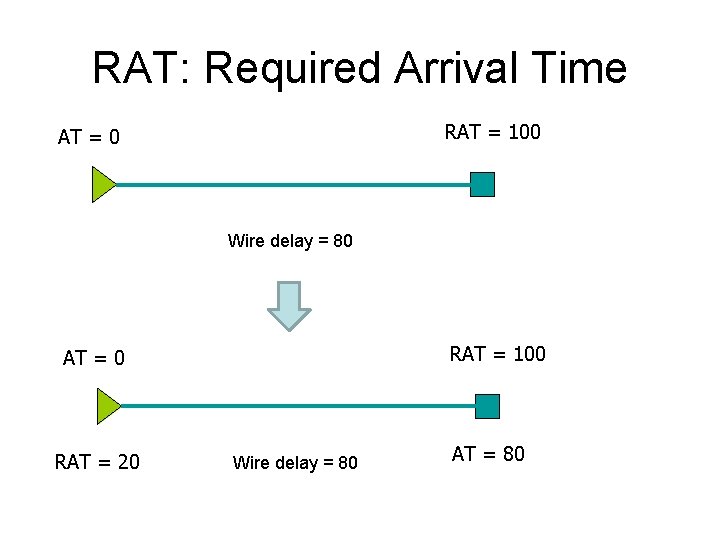
RAT: Required Arrival Time RAT = 100 AT = 0 Wire delay = 80 RAT = 100 AT = 0 RAT = 20 Wire delay = 80 AT = 80

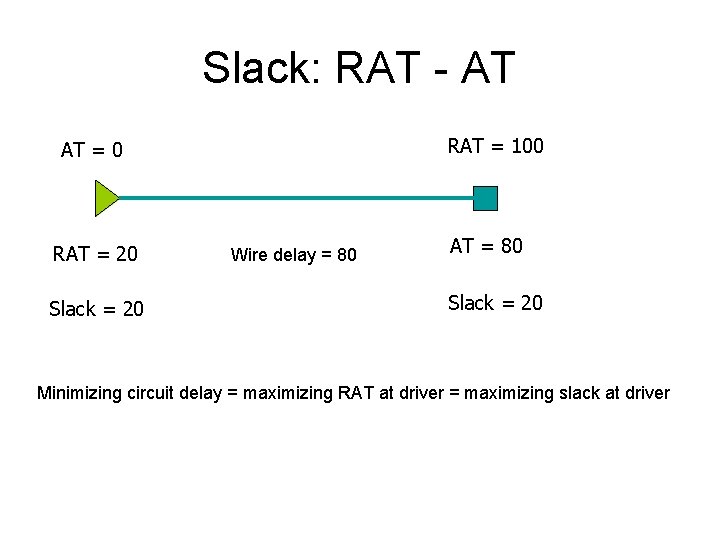
Slack: RAT - AT RAT = 100 AT = 0 RAT = 20 Slack = 20 Wire delay = 80 AT = 80 Slack = 20 Minimizing circuit delay = maximizing RAT at driver = maximizing slack at driver

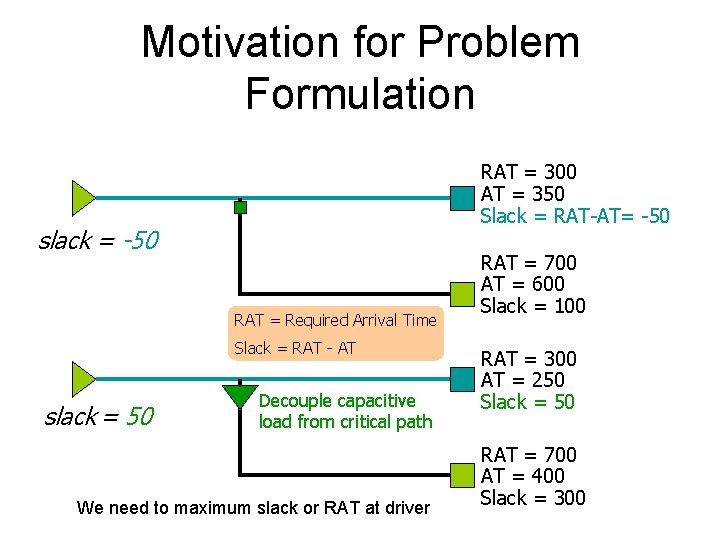
Motivation for Problem Formulation RAT = 300 AT = 350 Slack = RAT-AT= -50 slack = -50 RAT = Required Arrival Time Slack = RAT - AT slack = 50 Decouple capacitive load from critical path We need to maximum slack or RAT at driver RAT = 700 AT = 600 Slack = 100 RAT = 300 AT = 250 Slack = 50 RAT = 700 AT = 400 Slack = 300

Timing Driven Buffering Problem Formulation • Given – A Steiner tree – RAT at each sink – A buffer type – RC parameters – Candidate buffer locations • Find buffer insertion solution such that the slack (or RAT) at the driver is maximized

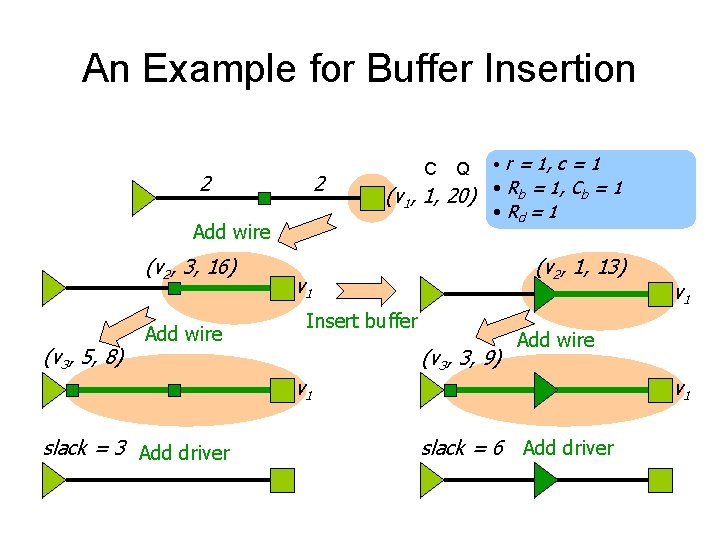
An Example for Buffer Insertion 2 2 (v 3, 5, 8) Add wire Q • r = 1, c = 1 (v 1, 1, 20) • Rb = 1, Cb = 1 • Rd = 1 Add wire (v 2, 3, 16) C (v 2, 1, 13) v 1 Insert buffer (v 3, 3, 9) Add wire v 1 slack = 3 Add driver v 1 slack = 6 Add driver

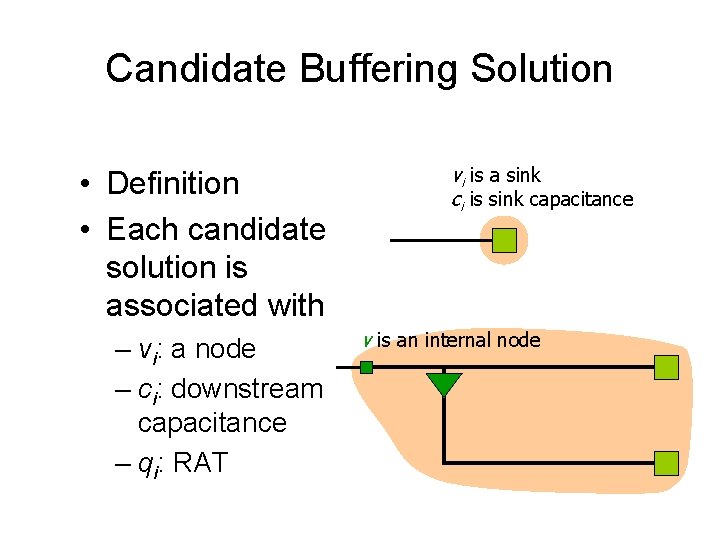
Candidate Buffering Solution • Definition • Each candidate solution is associated with – vi: a node – ci: downstream capacitance – qi: RAT vi is a sink ci is sink capacitance v is an internal node

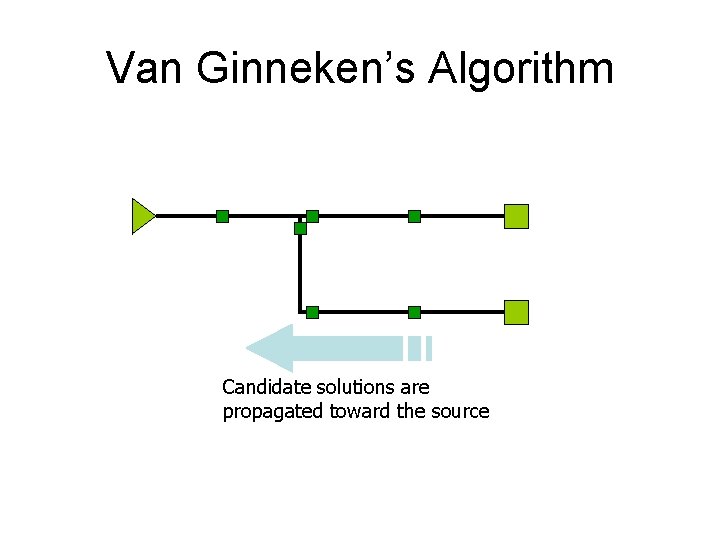
Van Ginneken’s Algorithm Candidate solutions are propagated toward the source

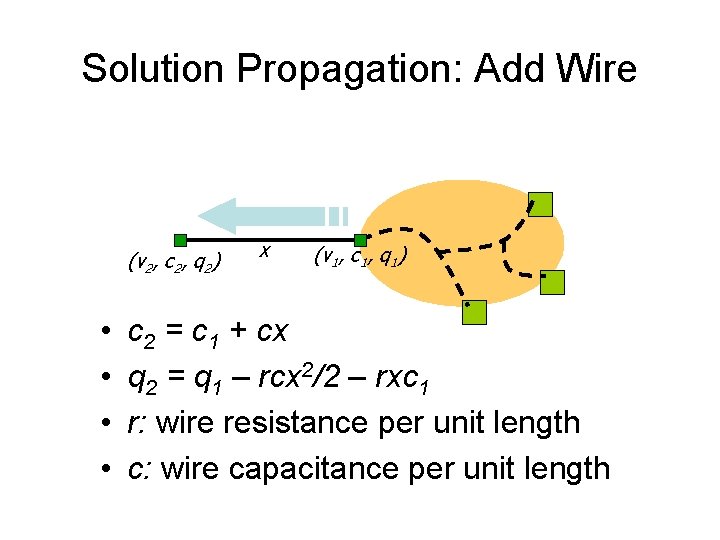
Solution Propagation: Add Wire (v 2, c 2, q 2) • • x (v 1, c 1, q 1) c 2 = c 1 + cx q 2 = q 1 – rcx 2/2 – rxc 1 r: wire resistance per unit length c: wire capacitance per unit length

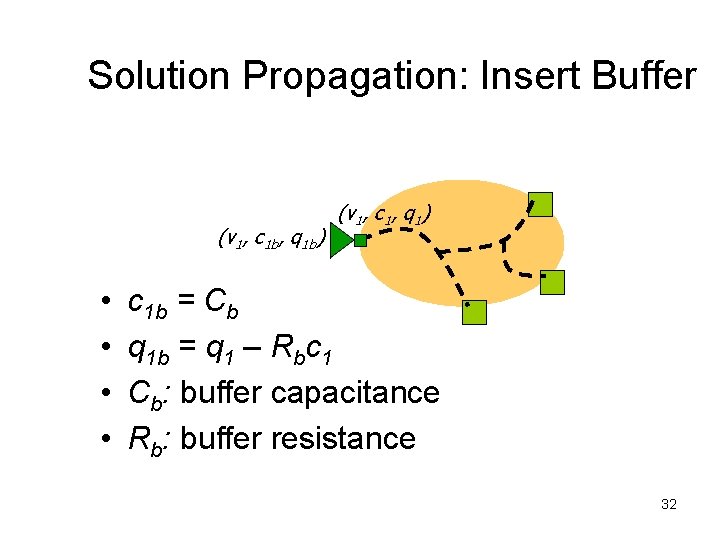
Solution Propagation: Insert Buffer (v 1, c 1 b, q 1 b) • • (v 1, c 1, q 1) c 1 b = Cb q 1 b = q 1 – Rbc 1 Cb: buffer capacitance Rb: buffer resistance 32

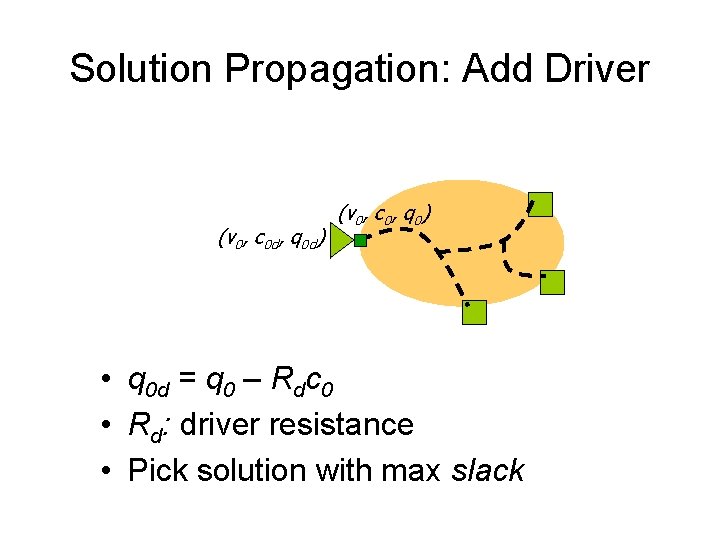
Solution Propagation: Add Driver (v 0, c 0 d, q 0 d) (v 0, c 0, q 0) • q 0 d = q 0 – Rdc 0 • Rd: driver resistance • Pick solution with max slack

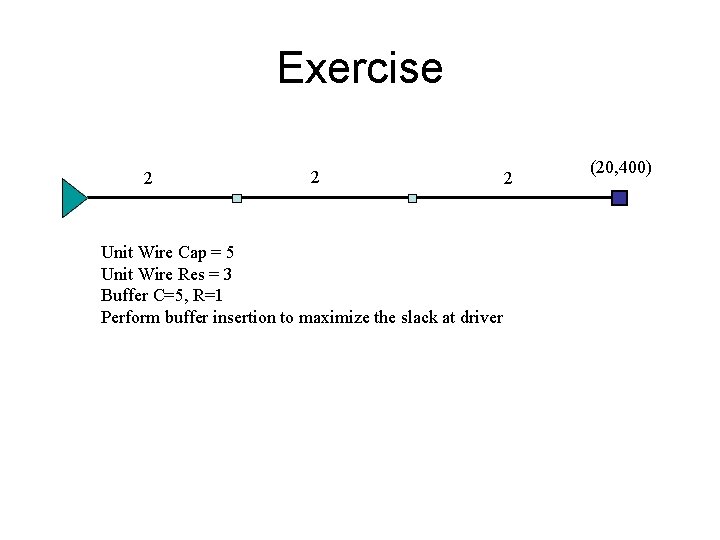
Exercise 2 2 Unit Wire Cap = 5 Unit Wire Res = 3 Buffer C=5, R=1 Perform buffer insertion to maximize the slack at driver 2 (20, 400)

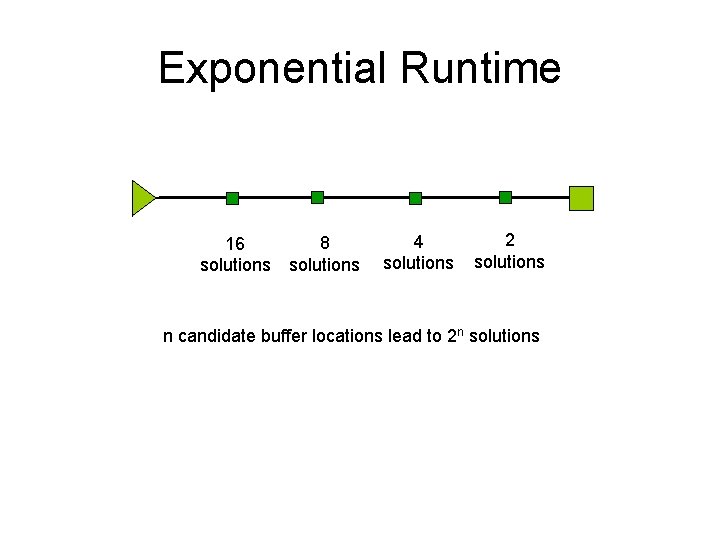
Exponential Runtime 16 solutions 8 solutions 4 solutions 2 solutions n candidate buffer locations lead to 2 n solutions

Solution Pruning • Two candidate solutions – (v, c 1, q 1) – (v, c 2, q 2) • Solution 1 is inferior if – c 1 c 2 : larger load – and q 1 q 2 : tighter timing

An Analogy - 1 LOAD Faster -> Smaller Delay -> Larger RAT (since RAT = RAToutput - Delay) Larger Load -> Larger Capacitance

An Analogy - 2 LOAD Faster & smaller load (larger RAT, smaller capacitance): Good Slower & larger load (smaller RAT, larger capacitance): Inferior END

An Analogy - 3 END Who will be the winner? Cannot tell at this moment, so keep both of them.

An Analogy - 4 END Who will be the winner? Cannot tell at this moment, so keep both of them.

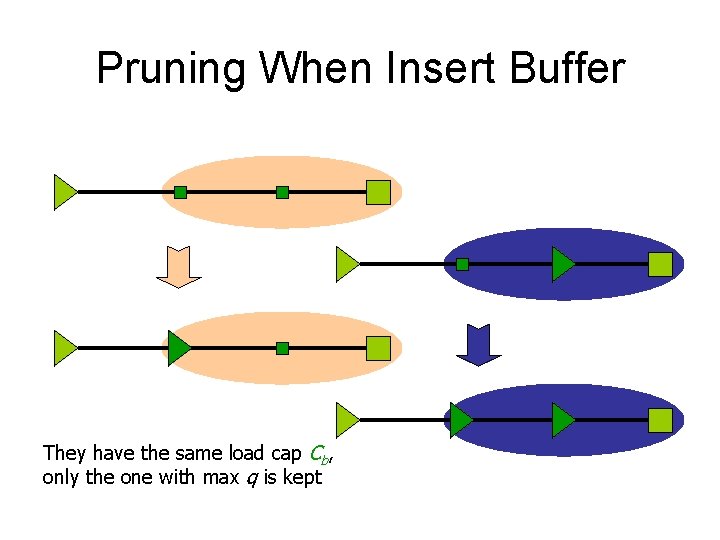
Pruning When Insert Buffer They have the same load cap Cb, only the one with max q is kept

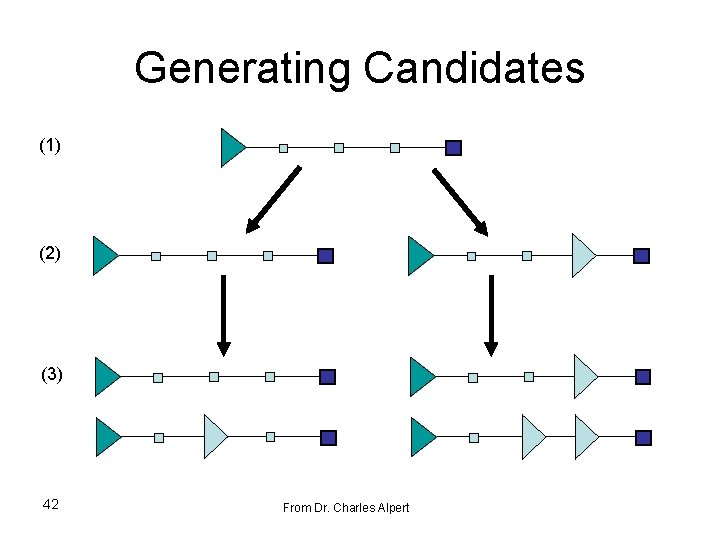
Generating Candidates (1) (2) (3) 42 From Dr. Charles Alpert

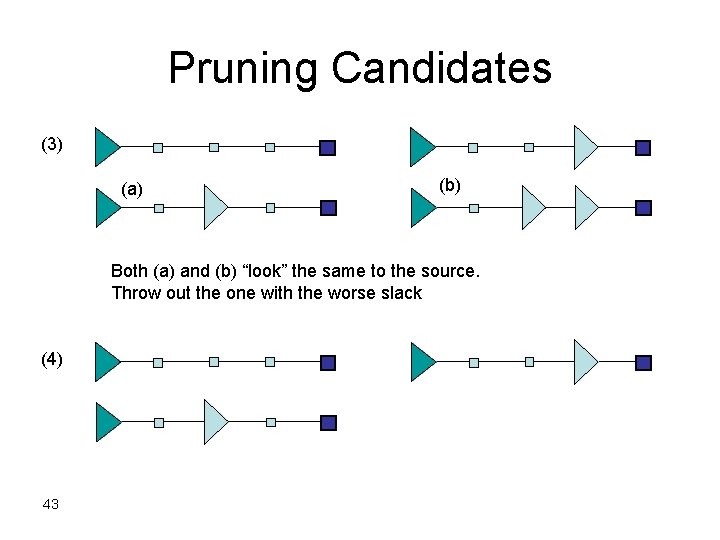
Pruning Candidates (3) (a) (b) Both (a) and (b) “look” the same to the source. Throw out the one with the worse slack (4) 43

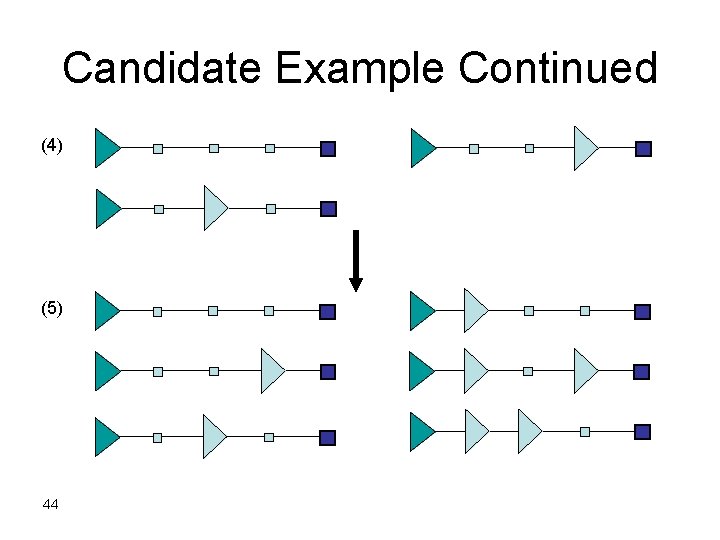
Candidate Example Continued (4) (5) 44

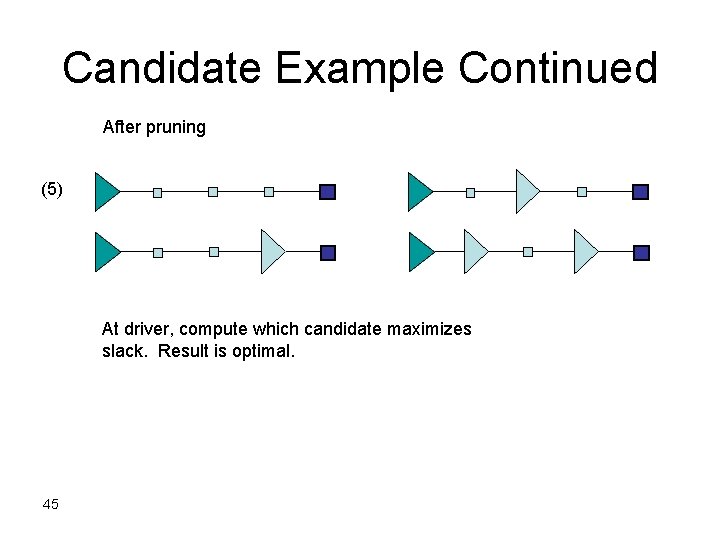
Candidate Example Continued After pruning (5) At driver, compute which candidate maximizes slack. Result is optimal. 45

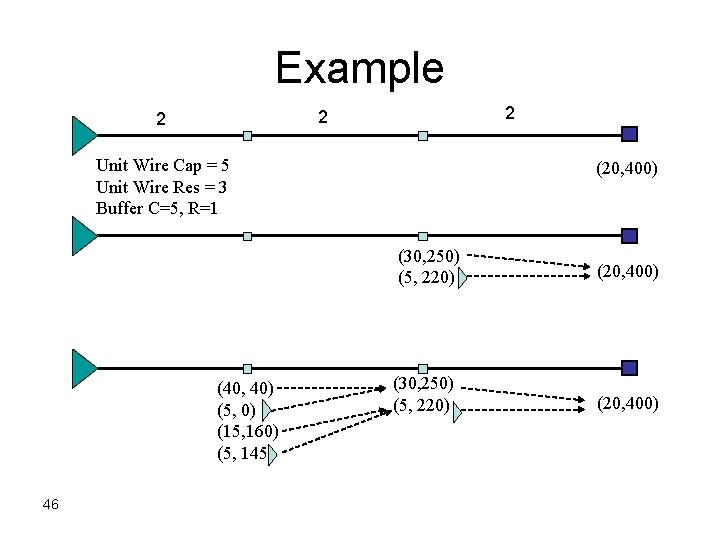
Example 2 2 2 Unit Wire Cap = 5 Unit Wire Res = 3 Buffer C=5, R=1 (20, 400) (30, 250) (5, 220) (40, 40) (5, 0) (15, 160) (5, 145) 46 (30, 250) (5, 220) (20, 400)

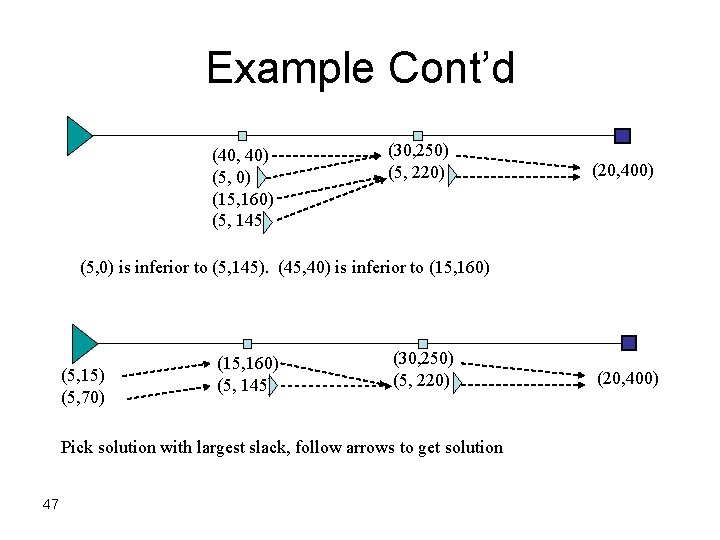
Example Cont’d (40, 40) (5, 0) (15, 160) (5, 145) (30, 250) (5, 220) (20, 400) (5, 0) is inferior to (5, 145). (45, 40) is inferior to (15, 160) (5, 15) (5, 70) (15, 160) (5, 145) (30, 250) (5, 220) Pick solution with largest slack, follow arrows to get solution 47 (20, 400)

Exercise • Without pruning, there will be exponential number of candidate solutions (i. e. , given n candidate buffer locations, there will be 2 n solutions). With pruning, how many solutions will we have?

Exercise • Continue the following buffer insertion process. Assume that all partial candidate buffering solutions are as shown. 2 Unit Wire Cap = 1 Unit Wire Res = 1 Buffer C=1, R=1 2 (10, 40) (8, 50) (5, 10) (15, 40) (7, 10) (9, 30) (12, 20)

Summary • Interconnect delay increases with technology scaling • Linear interconnect delay with buffer insertion • Buffer insertion with candidate buffer locations • Pruning for accelerating buffer insertion technique