EE 290 A Generalized Principal Component Analysis Lecture

EE 290 A: Generalized Principal Component Analysis Lecture 5: Generalized Principal Component Analysis Sastry & Yang © Spring, 2011 EE 290 A, University of California, Berkeley 1

Last time n n GPCA: Problem definition Segmentation of multiple hyperplanes Sastry & Yang © Spring, 2011 EE 290 A, University of California, Berkeley 2

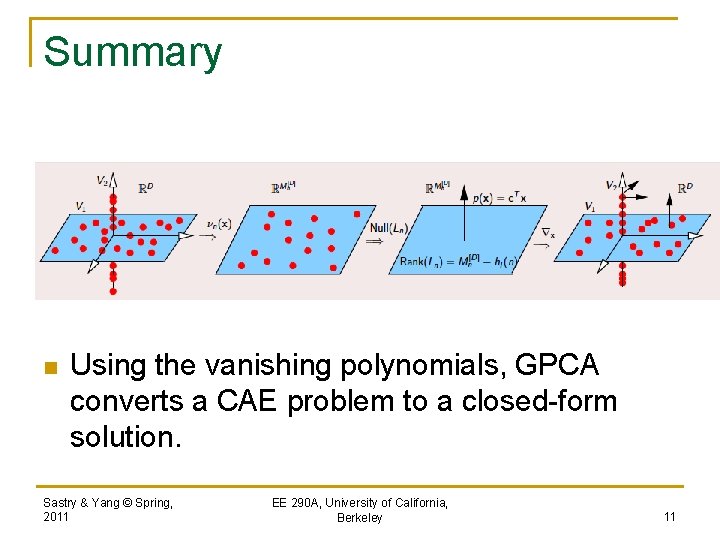
n Recover subspaces from vanishing polynomial Sastry & Yang © Spring, 2011 EE 290 A, University of California, Berkeley 3

Sastry & Yang © Spring, 2011 EE 290 A, University of California, Berkeley 4

Sastry & Yang © Spring, 2011 EE 290 A, University of California, Berkeley 5

This Lecture n n Segmentation of general subspace arrangements knowing the number of subspaces Subspace segmentation without knowing the number of subspaces Sastry & Yang © Spring, 2011 EE 290 A, University of California, Berkeley 6

An Introductory Example Sastry & Yang © Spring, 2011 EE 290 A, University of California, Berkeley 7

Make use of the vanishing polynomials Sastry & Yang © Spring, 2011 EE 290 A, University of California, Berkeley 8

Recover Mixture Subspace Models Sastry & Yang © Spring, 2011 EE 290 A, University of California, Berkeley 9

n Question: How to choose one representative point per subspace? (some loose answers) 1. 2. In noise-free case, randomly pick one. In noisy case, choose one close to the zero set of vanishing polynomials. (How? ) Sastry & Yang © Spring, 2011 EE 290 A, University of California, Berkeley 10

Summary n Using the vanishing polynomials, GPCA converts a CAE problem to a closed-form solution. Sastry & Yang © Spring, 2011 EE 290 A, University of California, Berkeley 11

Step 1: Fitting Polynomials n In general, when the dimensions of subspaces are mixed, the set of all K-th degree polynomials that vanish on A becomes more complicated. Sastry & Yang © Spring, 2011 EE 290 A, University of California, Berkeley 12

Polynomials may be dependent! Sastry & Yang © Spring, 2011 EE 290 A, University of California, Berkeley 13

n With the closed-form solution, even when the sample data are noisy, if K and subspace dimensions are known, a complete list of linearly independent vanishing polynomials can be recovered from the (null space of) embedded data matrix! Sastry & Yang © Spring, 2011 EE 290 A, University of California, Berkeley 14

Step 2: Polynomial Differentiation Sastry & Yang © Spring, 2011 EE 290 A, University of California, Berkeley 15

Step 3: Sample Point Selection n Given n sample points from K subspaces, how to choose one point per subspace to evaluate the orthonormal basis for each subspace? n What is the notion of optimality in choosing the best sample when a set of vanishing polynomials is given (for any algebraic set)? Sastry & Yang © Spring, 2011 EE 290 A, University of California, Berkeley 16

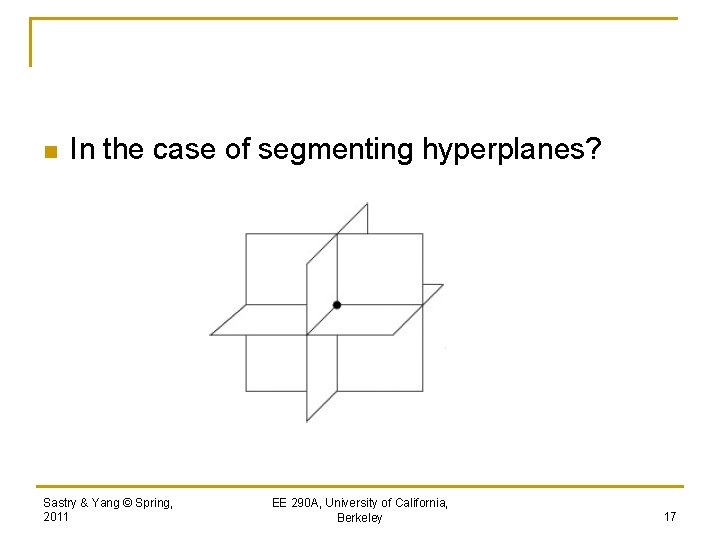
n In the case of segmenting hyperplanes? Sastry & Yang © Spring, 2011 EE 290 A, University of California, Berkeley 17

n Draw a random line that does not pass the origin Sastry & Yang © Spring, 2011 EE 290 A, University of California, Berkeley 18

Lemma 3. 9: For general arrangements n We shall choose samples as close to the zero set as possible (in the presence of noise) 1. 2. One shall avoid choosing points based on P(x), as it is merely an algebraic error, not the geometric distance. One shall discourage choosing points close to the intersection of two ore more subspaces, even when P(x)=0. Sastry & Yang © Spring, 2011 EE 290 A, University of California, Berkeley 19

Sastry & Yang © Spring, 2011 EE 290 A, University of California, Berkeley 20

Estimate the Rest (K-1) Subspaces n Polynomial division Sastry & Yang © Spring, 2011 EE 290 A, University of California, Berkeley 21

Sastry & Yang © Spring, 2011 EE 290 A, University of California, Berkeley 22

GPCA without knowing K or d’s n Determining K and d’s is straightforward when subspaces are of equal dimension 1. 2. 3. If d is known, project samples to (d+1)-dim space. The problem becomes hyperplane segmentation. If K is known, project samples to l-dim spaces, while l=1, 2, …, compute k-th order Veronese map until it drops rank. If both K and d are unknown, try all the combinations Sastry & Yang © Spring, 2011 EE 290 A, University of California, Berkeley 23

GPCA without knowing K or d’s n Determine arrangements of different dimensions 1. If data are noise-free, check the Hilbert function table. Sastry & Yang © Spring, 2011 EE 290 A, University of California, Berkeley 24

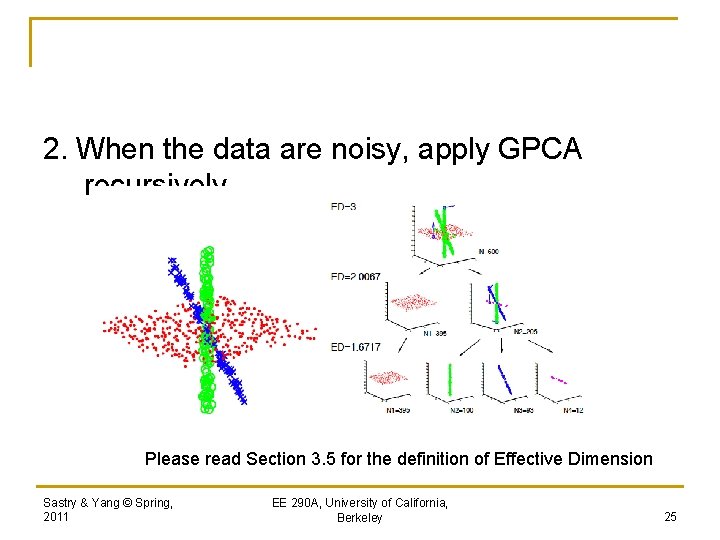
2. When the data are noisy, apply GPCA recursively Please read Section 3. 5 for the definition of Effective Dimension Sastry & Yang © Spring, 2011 EE 290 A, University of California, Berkeley 25