EE 201 A Starting 2005 called EE 201

EE 201 A (Starting 2005, called EE 201 B) Modeling and Optimization for VLSI Layout UCLA Instructor: Lei He Email: LHE@ee. ucla. edu

Chapter 9 n Transistor/gate n Buffer sizing * Insertion * Part of slides is provided by Prof. Sapatnekar from U. of Minnesota.

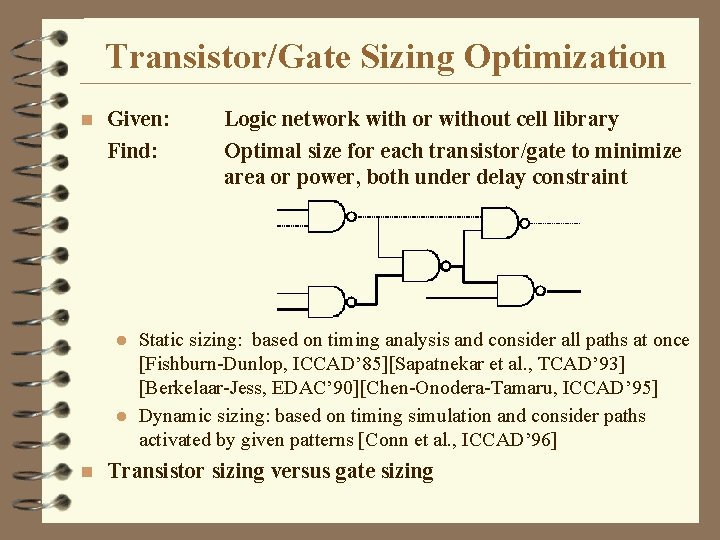
Transistor/Gate Sizing Optimization n Given: Find: Logic network with or without cell library Optimal size for each transistor/gate to minimize area or power, both under delay constraint Static sizing: based on timing analysis and consider all paths at once [Fishburn-Dunlop, ICCAD’ 85][Sapatnekar et al. , TCAD’ 93] [Berkelaar-Jess, EDAC’ 90][Chen-Onodera-Tamaru, ICCAD’ 95] l Dynamic sizing: based on timing simulation and consider paths activated by given patterns [Conn et al. , ICCAD’ 96] l n Transistor sizing versus gate sizing

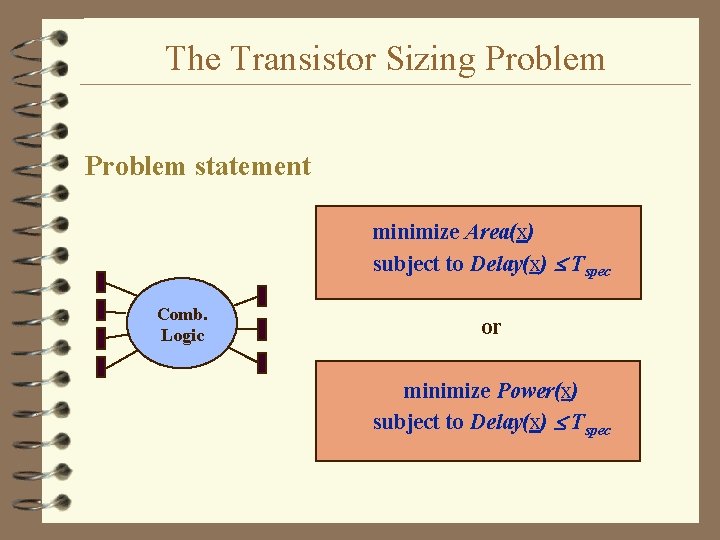
The Transistor Sizing Problem statement minimize Area(x) subject to Delay(x) Tspec Comb. Logic or minimize Power(x) subject to Delay(x) Tspec

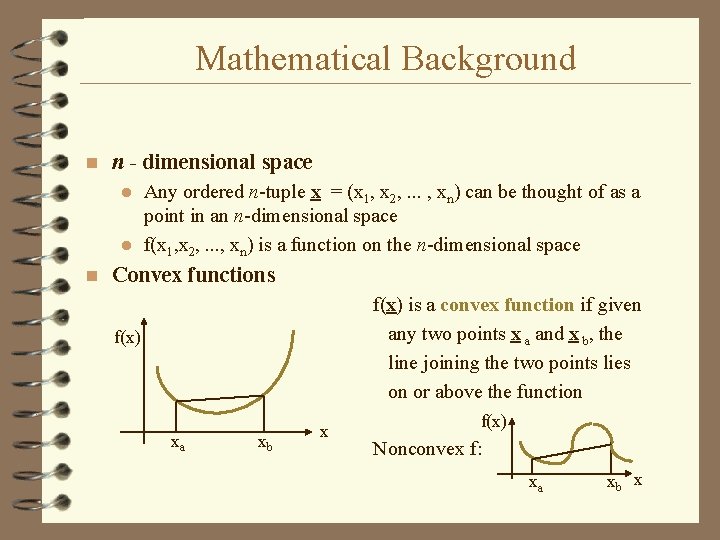
Mathematical Background n n - dimensional space Any ordered n-tuple x = (x 1, x 2, . . . , xn) can be thought of as a point in an n-dimensional space l f(x 1, x 2, . . . , xn) is a function on the n-dimensional space l n Convex functions f(x) is a convex function if given any two points x a and x b, the line joining the two points lies on or above the function f(x) xa xb x f(x) Nonconvex f: xa xb x

Math Background (Contd. ) n Convex functions in two dimensions f(x 1, x 2) = x 12 + x 22 Formally, f(x) is convex if f( xa + [1 - ] xb) f(xa) + [1 - ] f(xb) 0 1

Math Background (Contd. ) n Convex sets A set S is a convex set if given any two points xa and xb in the set, the line joining the two points lies entirely within the set n Examples Shape of Wyoming n Shape of a pizza Nonconvex Sets Shape of CA Silhouette of the Taj Mahal

Math Background (Contd. ) n Mathematical characterization of a convex set S l If x 1, x 2 S, then x 1 + (1 - ) x 2 S, for 0 1 x 2 If f(x) is a convex function, f(x) c is a convex set n An intersection of convex sets is a convex set n

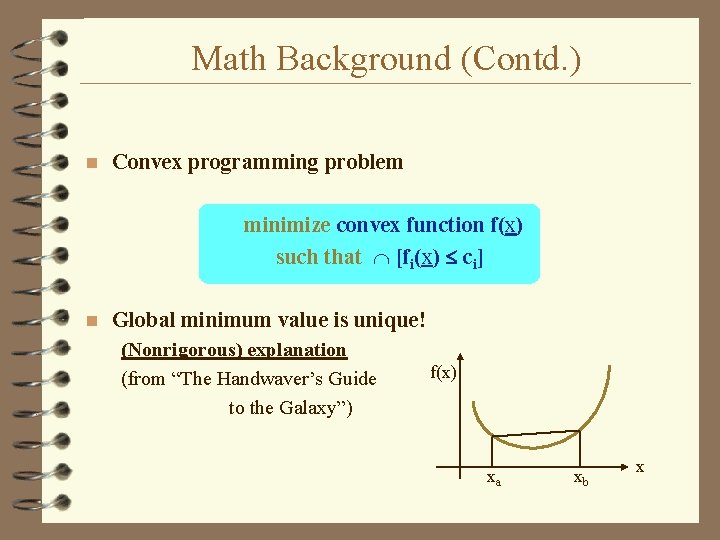
Math Background (Contd. ) n Convex programming problem minimize convex function f(x) such that [fi(x) ci] n Global minimum value is unique! (Nonrigorous) explanation (from “The Handwaver’s Guide to the Galaxy”) f(x) xa xb x

Math Background (Contd. in English) n A posynomial is like a polynomial except all coefficients are positive l exponents could be real numbers (positive or negative) l n Are these posynomials? 6. 023 x 11. 23 + 4. 56 x 13. 4 x 27. 89 x 3 -0. 12 YES x 1 - 9. 78 x 24. 2 x 3 -9. 1 NO (x 1 + 2 x 2 + 2 x 3 + 5)/x 1 + (x 3 + 2 x 4 + 3)/x 3 YES

Math Background (Contd. ) n In any posynomial function f(x 1, x 2, . . . , xn), substitute xi = exp(zi) to get F(z 1, z 2, . . . , zn) n Then F(z 1, z 2, . . . , zn) = convex function in (z 1, . . . , zn) ! minimize (posynomial objective in xi’s) s. t. (posynomial function in xi’s)i K for 1 i m [xi = exp(zi)] minimize (convex objective) over a convex set Therefore, any local minimum is a global minimum!

Properties of Tr. Sizing under the Elmore Model n x is the set (vector) of transistor sizes minimize Area(x) subject to Delay(x) Tspec n Area(x) = i = 1 to n x i n Each path delay = R C (posynomial!) R xi-1, C xi posynomial path delay function l Delay(x) Tspec Pathdelay(x) Tspec for all paths l n Therefore, problem has a unique global min. value

TILOS™ (TImed LOgic Synthesis) n Philosophy l Since min. value is unique, a simple method should find it! Problem minimize Area(x) subject to Delay(x) Tspec n Strategy n Set all transistors in the circuit to minimum size l Find the critical path (largest delay path) l Reduce delay of critical path, but with a minimal increase in the objective function value l (TILOS™ is a registered trademark of Lucent Technologies)

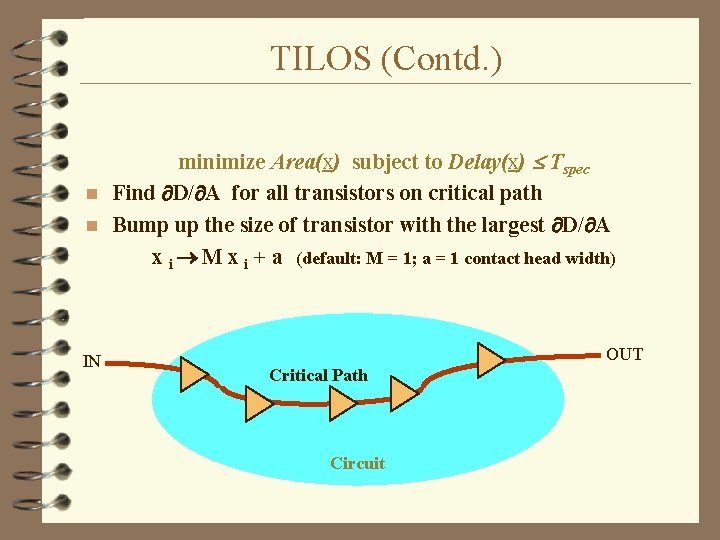
TILOS (Contd. ) minimize Area(x) subject to Delay(x) Tspec n Find D/ A for all transistors on critical path n Bump up the size of transistor with the largest D/ A x i M x i + a (default: M = 1; a = 1 contact head width) IN OUT Critical Path Circuit

Sensitivity Computation Rprev “ 1” C w n D(w) = K + Rprev (Cu. w) + Ru. C / w n D/ w = Rprev. Cu - Ru. C / w 2 Could minimize path delay by setting derivative to zero n Problem: may cause another path delay to become very high! n

Why Isn’t This THE Perfect Solution? n Problems with interacting paths B C A D (1) Better to size A than to size all of B, C and D (2) If X-E is near-critical and A-D is critical, size A (not D) E X False paths, layout considerations not incorporated n AND YET. . n TILOS (the commercial tool) gives good solutions l It has handled circuits with 250 K transistors l It has linear time performance with increasing circuit size l

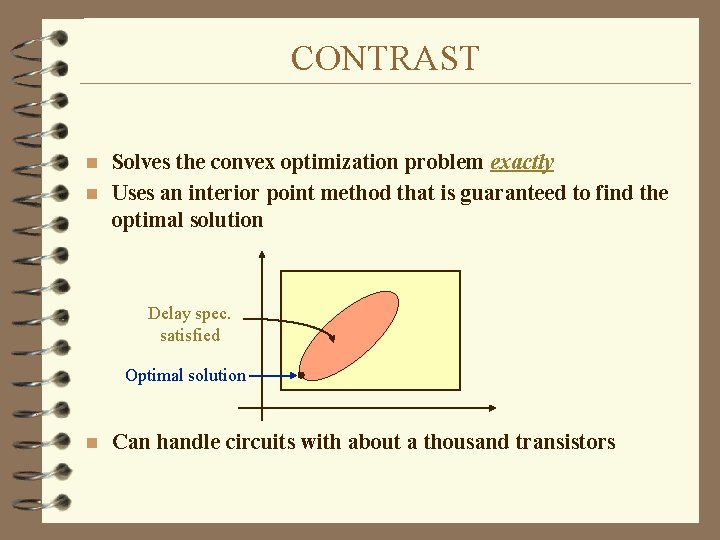
CONTRAST Solves the convex optimization problem exactly n Uses an interior point method that is guaranteed to find the optimal solution n Delay spec. satisfied Optimal solution n Can handle circuits with about a thousand transistors

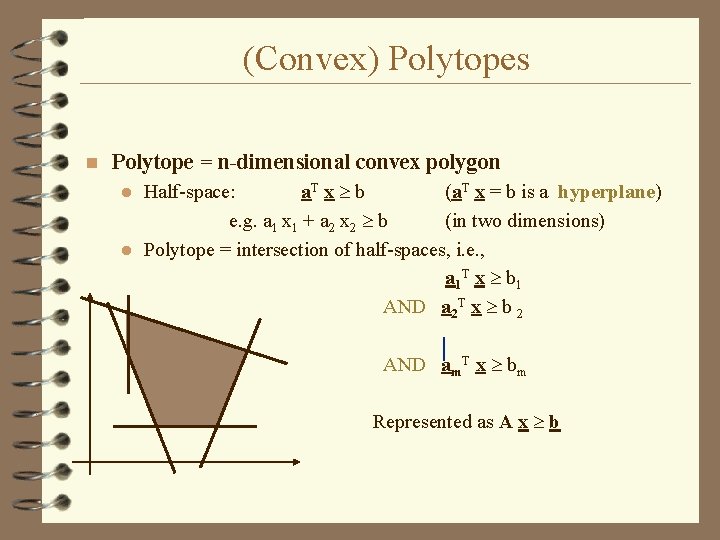
(Convex) Polytopes n Polytope = n-dimensional convex polygon Half-space: a. T x b (a. T x = b is a hyperplane) e. g. a 1 x 1 + a 2 x 2 b (in two dimensions) l Polytope = intersection of half-spaces, i. e. , a 1 T x b 1 AND a 2 T x b 2 l AND am. T x bm Represented as A x b

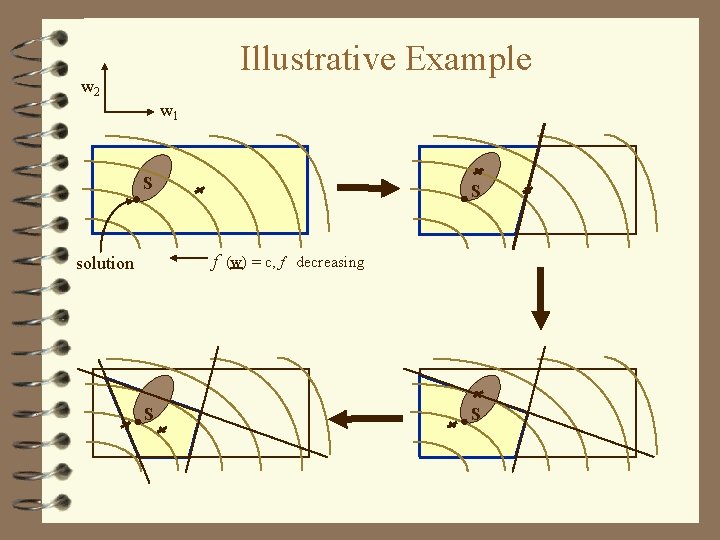
Convex Optimization Algorithm (Vaidya) (1) Enclose solution within a polytope (invariant) l Typically, take a “box” represented by wi w. MAX and wi w. MIN as the starting polytope. (2) Find center of polytope, wc (3) Does wc satisfy constraints (timing specs)? l Take transistor widths corresponding to wc and perform a static timing analysis (4) Add a hyperplane through the center so that the solution lies entirely in one half-space l Hyperplane equation depends on feasibility of wc

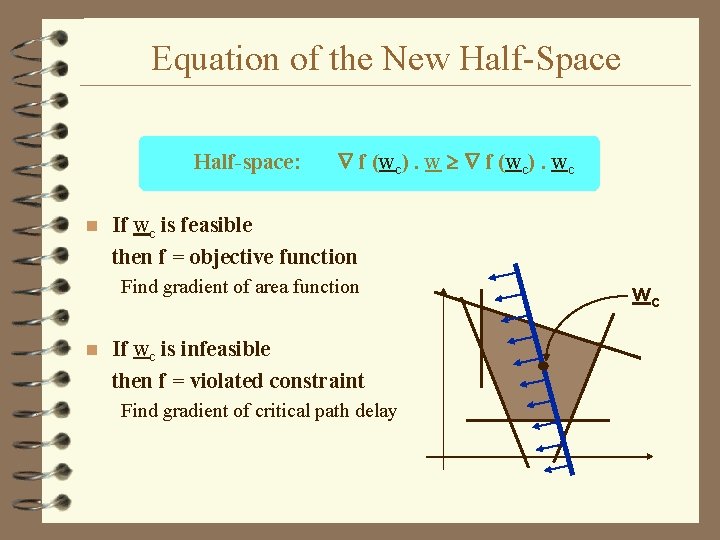
Equation of the New Half-Space Half-space: n f (wc). wc If wc is feasible then f = objective function Find gradient of area function n If wc is infeasible then f = violated constraint Find gradient of critical path delay wc

Illustrative Example w 2 w 1 S S f (w) = c, f decreasing solution S S

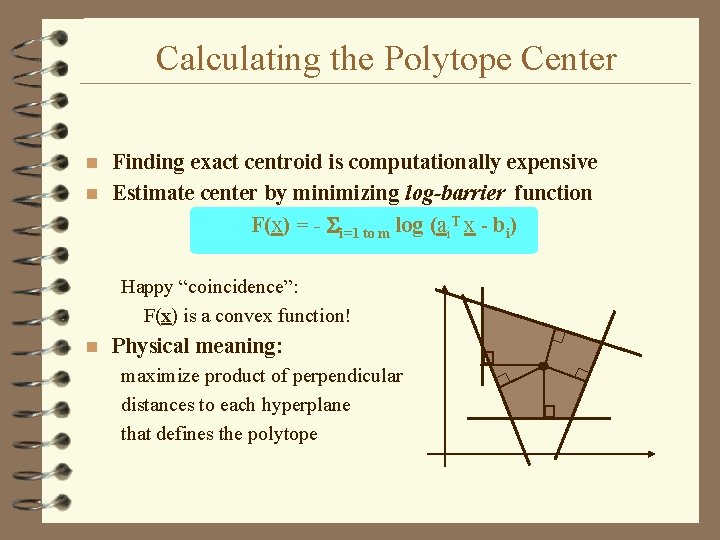
Calculating the Polytope Center Finding exact centroid is computationally expensive n Estimate center by minimizing log-barrier function F(x) = - i=1 to m log (ai. T x - bi) n Happy “coincidence”: F(x) is a convex function! n Physical meaning: maximize product of perpendicular distances to each hyperplane that defines the polytope

Linear Programming Methods n LP-based approaches l Delay Model gate delay as a piecewise linear function Parameters: • transistor widths wn , wp • fanout transistor widths • input transition time wn Formulate problem as a linear program (LP) l Use an efficient simplex package to solve LP l

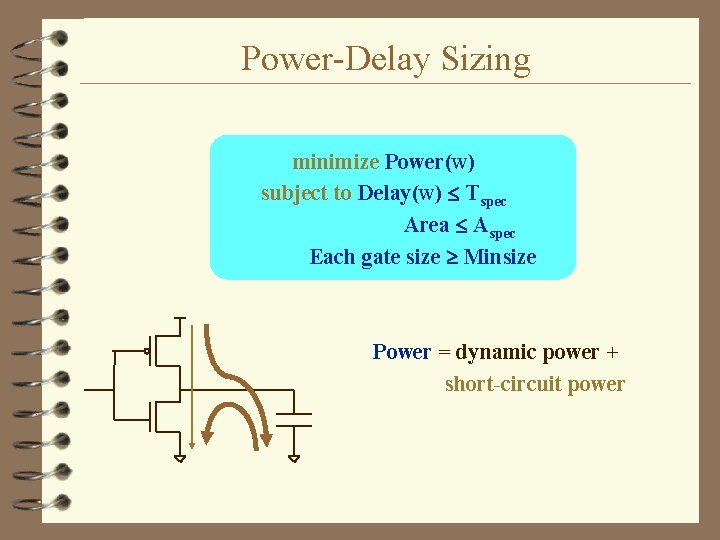
Power-Delay Sizing minimize Power(w) subject to Delay(w) Tspec Area Aspec Each gate size Minsize Power = dynamic power + short-circuit power

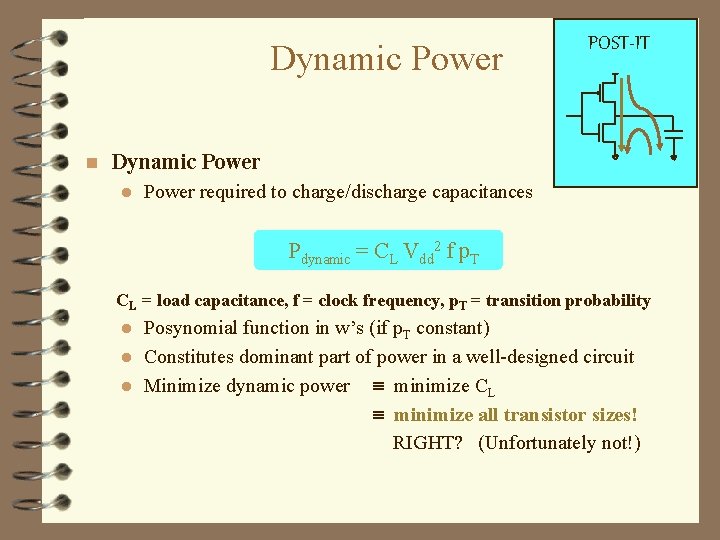
Dynamic Power n POST-IT Dynamic Power l Power required to charge/discharge capacitances Pdynamic = CL Vdd 2 f p. T CL = load capacitance, f = clock frequency, p. T = transition probability Posynomial function in w’s (if p. T constant) l Constitutes dominant part of power in a well-designed circuit l Minimize dynamic power minimize CL minimize all transistor sizes! RIGHT? (Unfortunately not!) l

Short-Circuit Power n POST-IT Short-circuit Power dissipated when a direct Vdd-ground path exists l Approximate formula by Veendrick (many assumptions) l Pshort-ckt = Vdd -2 VT)2 f p. T = transconductance, = transition time Posynomial function in w’s (if p. T const) l Other (more accurate) models: table lookup, curve-fitting l “Less than 10 -20% of total power in a well-designed circuit” l So what’s the catch? l

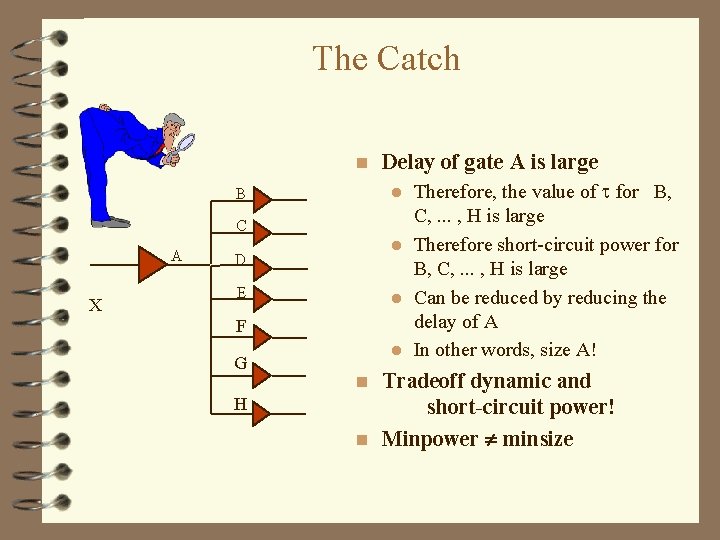
The Catch n Therefore, the value of for B, C, . . . , H is large l Therefore short-circuit power for B, C, . . . , H is large l Can be reduced by reducing the delay of A l In other words, size A! l B C A X D E F G H Delay of gate A is large Tradeoff dynamic and short-circuit power! n Minpower minsize n

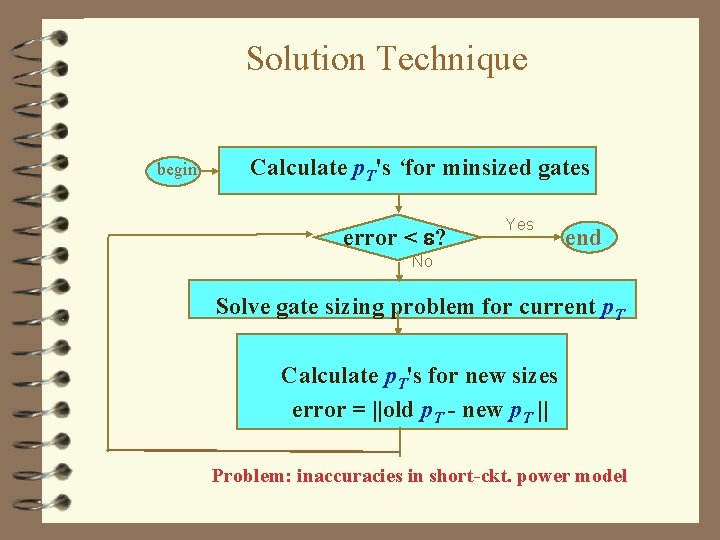
Solution Technique begin Calculate p. T's ‘for minsized gates error < ? Yes end No Solve gate sizing problem for current p. T Calculate p. T's for new sizes error = ||old p. T - new p. T || Problem: inaccuracies in short-ckt. power model

Transistor/Gate Sizing [Borah-Owens-Irwin, ISLPD’ 95, TCAD’ 96] Optimal transistor size CI = int. cap

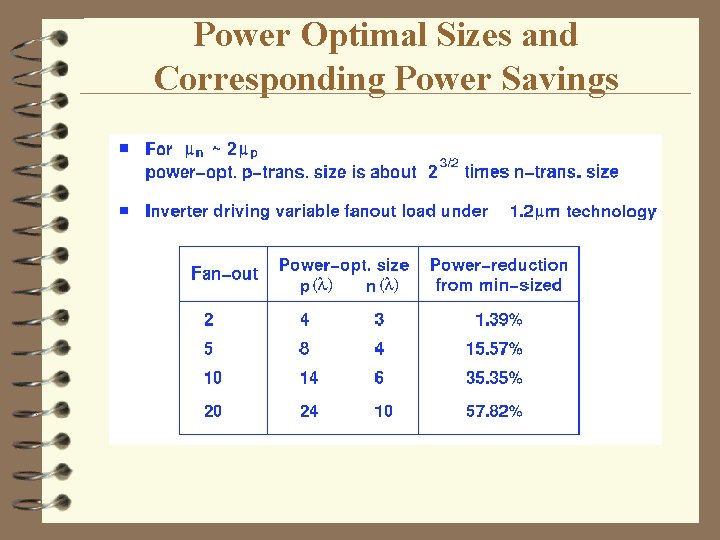
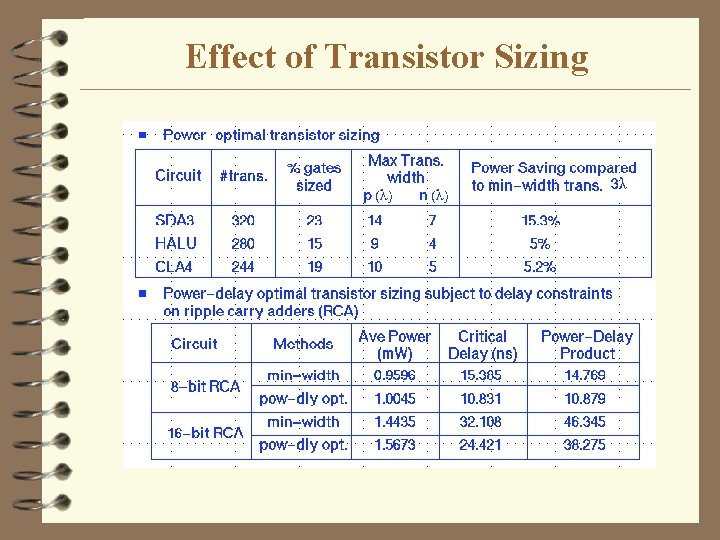
Power Optimal Sizes and Corresponding Power Savings

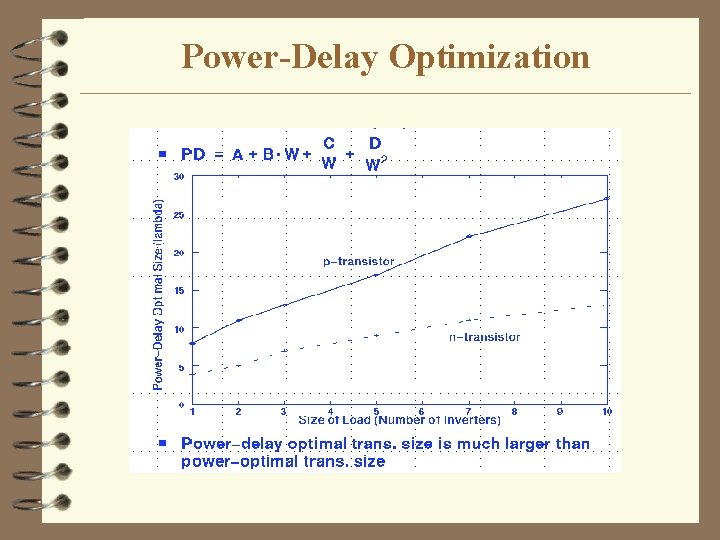
Power-Delay Optimization

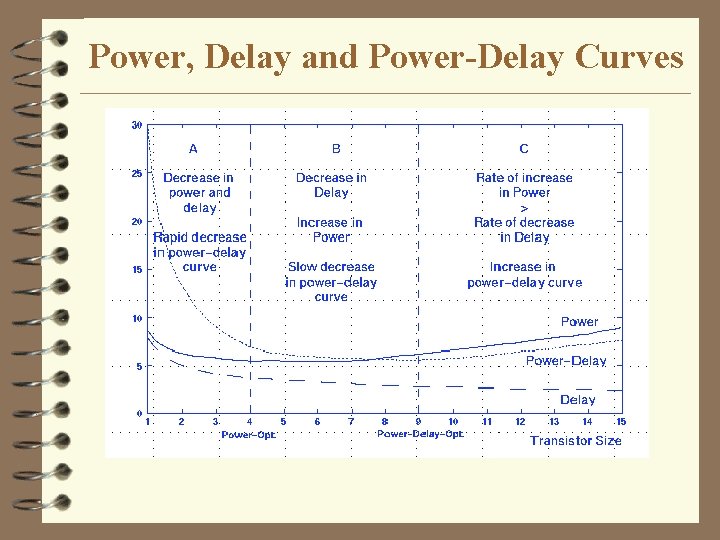
Power, Delay and Power-Delay Curves

Power-Delay Optimal Transistor Sizing Algorithm Power-Optimal initial sizing n Timing analysis n While exists path-delay > target-delay n Power-delay optimal sizing critical path l if path-delay > target-delay - upsize transistor with minimum power-delay slope l if path-delay < target-delay - downsize transistor with minimum power-delay slope l Incremental timing analysis l

Effect of Transistor Sizing