EE 193 Parallel Computing Fall 2017 Tufts University

EE 193: Parallel Computing Fall 2017 Tufts University Instructor: Joel Grodstein joel. grodstein@tufts. edu Lecture 7: Matrix multiply 1

Goals • Primary goals: – Understand block-matrix algorithms 2

Matrix multiplication • Matrix multiplication is the poster child for parallel computation. Some uses: – Computer graphics (e. g. , linear algebra for transforming points between coordinate spaces) – Anything that uses linear algebra – Neural nets (perhaps the biggest use of GPGPUs) • And that's good – because matrix multiplication is easy, right? – It's easy to get it correct. – But not so easy to make it fast. EE 193 Joel Grodstein 3

Matrix times vector • Let's start simple: a (4 x 4 matrix) * (1 x 4 vector) Write the eqns. Write the code. A 00 A 01 A 02 A 03 x 0 y 0 A 11 A 12 A 13 x 1 y 1 * = A 20 A 21 A 22 A 23 x 2 y 2 A 30 A 31 A 32 A 33 x 3 y 3 for r=0…N-1 for k=0…N-1 y[r] += A[r, k]*x[k]; If N were big, what do you think about the temporal and spatial locality of this code? EE 193 Joel Grodstein 4

Matrix times vector A 00 A 01 A 02 A 03 x 0 y 0 for r=0…N-1 A 10 A 11 A 12 A 13 x 1 y 0 for k=0…N-1 * = A 20 A 21 A 22 A 23 x 2 y[r] += A[r, k]*x[k]; A 30 A 31 A 32 A 33 x 3 y 3 • Temporal: – each element of A is used only once . – each element of x is used N times . – this is only useful if x fits into cache (hopefully easy) • Spatial: – The inner loop accesses memory in row-major order EE 193 Joel Grodstein 5

Data for HSX and Pascal Haswell Server Nvidia Pascal P 100 # cores 18 3840 Die area 660 mm 2 (22 nm) 610 mm 2 (16 nm) Frequency 2. 3 GHz normal 1. 3 GHz Max DRAM BW 100 GB/s 720 GB/s LLC size 2. 5 MB/core (L 3) 4 MB L 2/chip LLC-1 size 256 K/core(L 2) 64 KB/SM (64 cores) Registers/core 180 (2 threads/core) 500 Power 165 watts 300 watts Company market cap $160 B $90 B • Look at Haswell server compute and memory EE 193 Joel Grodstein 6

Xeon compute-to-memory ratio • EE 193 Joel Grodstein 7

Compute/memory ratio A 00 A 01 A 02 A 03 x 0 y 0 for i=0…N-1 A 10 A 11 A 12 A 13 x 1 y 0 for k=0…N-1 * = A 20 A 21 A 22 A 23 x 2 y[i] += A[i, k]*y[k]; A 30 A 31 A 32 A 33 x 3 y 3 • • How many computations are there? N 2 FMACs. How many floats are read/written? N 2 +2 N The compute/memory ratio is Roughly 1 We want every piece of data to be be reused 4 times – but it’s only used once, period • So a Xeon cannot get data in from memory fast enough to keep the FPUs busy . – Even perfect caches cannot fix this! EE 193 Joel Grodstein 8

What does it all mean? • Big-data problems do not fit in your registers. – They're unlikely to fit in L 1. – They may fit in L 2… or L 3… or main memory… • If they fit into L 1, all of this is irrelevant – since the BW and latency from L 1 to RF is so good. • If they fit into main memory… – A chain is no stronger than its weak link. – Cache can buffer, reuse, even out flow, etc. – If the compute/memory ratio is <5, then HSX cannot use all of its computes – But if the average DRAM bandwidth is the weak link, there is no way to fix that. EE 193 Joel Grodstein 9

A slightly different problem A 00 A 01 A 02 A 03 x 0 y 0 for i=0…N-1 A 10 A 11 A 12 A 13 x 1 y 0 for k=0…N-1 * = A 20 A 21 A 22 A 23 x 2 y[i] += A[i, k]*x[k]; A 30 A 31 A 32 A 33 x 3 y 3 • Related problem: what if A is fixed, and we want to stream in lots of x vectors. • Consider the work for one vector x producing one vector y, and assuming A is already in cache. • How many computations are there? N 2 FMACs. • How many floats are read/written? 2 N • The compute/memory ratio is N/2 • So HSX can deal with this for N≥ 10. • Note that computer graphics only typically has N=4. But the graphics pipeline has more than just one matrix multiply. EE 193 Joel Grodstein 10

More on matrix*vector A 00 A 01 A 02 A 03 x 0 y 0 for i=0…N-1 A 10 A 11 A 12 A 13 x 1 y 0 for k=0…N-1 * = A 20 A 21 A 22 A 23 x 2 y[i] += A[i, k]*x[k]; A 30 A 31 A 32 A 33 x 3 y 3 • Keep looking at the same problem: A is fixed, and we want to stream in lots of x vectors. • In this example, do we have any need for caches? – We need someplace to store the A matrix. – Our code may not wind up accessing the various x vectors exactly in address-sequential order; a cache can store the ones we skip until we use them. EE 193 Joel Grodstein 11

Matrix times matrix • Let's move on to a bigger problem: matrix*matrix A 00 A 01 A 02 A 03 A 10 A 11 A 12 A 13 * A 20 A 21 A 22 A 23 A 30 A 31 A 32 A 33 B 00 B 01 B 02 B 03 B 10 B 11 B 12 B 13 = B 20 B 21 B 22 B 23 B 30 B 31 B 32 B 33 C 00 C 01 C 02 C 03 C 10 C 11 C 12 C 13 C 20 C 21 C 22 C 23 C 30 C 31 C 32 C 33 for r=0…N-1 for c=0…N-1 for k=0…N-1 C[r, c] += A[r, k]*B[k, c]; EE 193 Joel Grodstein 12

Matrix times matrix • Let's move on to a bigger problem: matrix*matrix A 00 A 01 A 02 A 03 A 10 A 11 A 12 A 13 A 20 A 21 A 22 A 23 A 30 A 31 A 32 A 33 * B 00 B 01 B 02 B 03 B 10 B 11 B 12 B 13 B 20 B 21 B 22 B 23 B 30 B 31 B 32 B 33 = C 00 C 01 C 02 C 03 C 10 C 11 C 12 C 13 C 20 C 21 C 22 C 23 C 30 C 31 C 32 C 33 How many computations are there? N 3 FMACs How many floats are read/written? 3 N 2 The compute/memory ratio is N/3. So, in principle, this for r=0…N-1 should be easy! for c=0…N-1 for k=0…N-1 C[r, c] += A[r, k]*B[k, c]; EE 193 Joel Grodstein 13

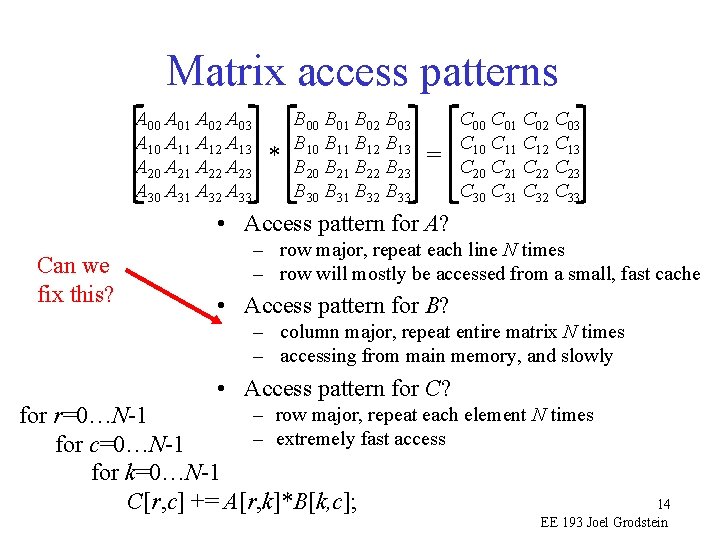
Matrix access patterns A 00 A 01 A 02 A 03 A 10 A 11 A 12 A 13 A 20 A 21 A 22 A 23 A 30 A 31 A 32 A 33 * B 00 B 01 B 02 B 03 B 10 B 11 B 12 B 13 B 20 B 21 B 22 B 23 B 30 B 31 B 32 B 33 = C 00 C 01 C 02 C 03 C 10 C 11 C 12 C 13 C 20 C 21 C 22 C 23 C 30 C 31 C 32 C 33 • Access pattern for A? Can we fix this? – row major, repeat each line N times – row will mostly be accessed from a small, fast cache • Access pattern for B? – column major, repeat entire matrix N times – accessing from main memory, and slowly • Access pattern for C? – row major, repeat each element N times for r=0…N-1 – extremely fast access for c=0…N-1 for k=0…N-1 C[r, c] += A[r, k]*B[k, c]; 14 EE 193 Joel Grodstein

A 00 A 01 A 02 A 03 A 10 A 11 A 12 A 13 A 20 A 21 A 22 A 23 A 30 A 31 A 32 A 33 * B 00 B 01 B 02 B 03 B 10 B 11 B 12 B 13 B 20 B 21 B 22 B 23 B 30 B 31 B 32 B 33 = C 00 C 01 C 02 C 03 C 10 C 11 C 12 C 13 C 20 C 21 C 22 C 23 C 30 C 31 C 32 C 33 for r=0…N-1 for c=0…N-1 for k=0…N-1 C[r, c] += A[r, k]*B[k, c]; • Our trick: swap the 2 nd and 3 rd loops. • Any change in the end-result computation? – We still execute the final line with the same r, c, k triplets; just in a different order. And adding the same numbers in a different order doesn't change the result. EE 193 Joel Grodstein 15

In-class exercise • Draw matrix multiple for 2 x 2 matrices on the board • Divide the class into two groups – one group works on the original loop ordering, and the other on the swapped ordering • Each group manually runs the code, and notes which A*B products got summed into which locations in C. • At the end, compare to see if they both added the same product pairs EE 193 Joel Grodstein 16

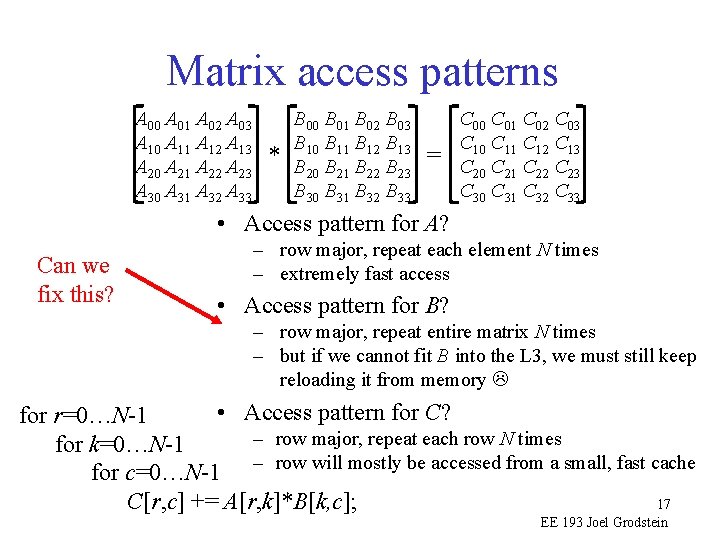
Matrix access patterns A 00 A 01 A 02 A 03 A 10 A 11 A 12 A 13 A 20 A 21 A 22 A 23 A 30 A 31 A 32 A 33 * B 00 B 01 B 02 B 03 B 10 B 11 B 12 B 13 B 20 B 21 B 22 B 23 B 30 B 31 B 32 B 33 = C 00 C 01 C 02 C 03 C 10 C 11 C 12 C 13 C 20 C 21 C 22 C 23 C 30 C 31 C 32 C 33 • Access pattern for A? Can we fix this? – row major, repeat each element N times – extremely fast access • Access pattern for B? – row major, repeat entire matrix N times – but if we cannot fit B into the L 3, we must still keep reloading it from memory • Access pattern for C? for r=0…N-1 – row major, repeat each row N times for k=0…N-1 for c=0…N-1 – row will mostly be accessed from a small, fast cache 17 C[r, c] += A[r, k]*B[k, c]; EE 193 Joel Grodstein

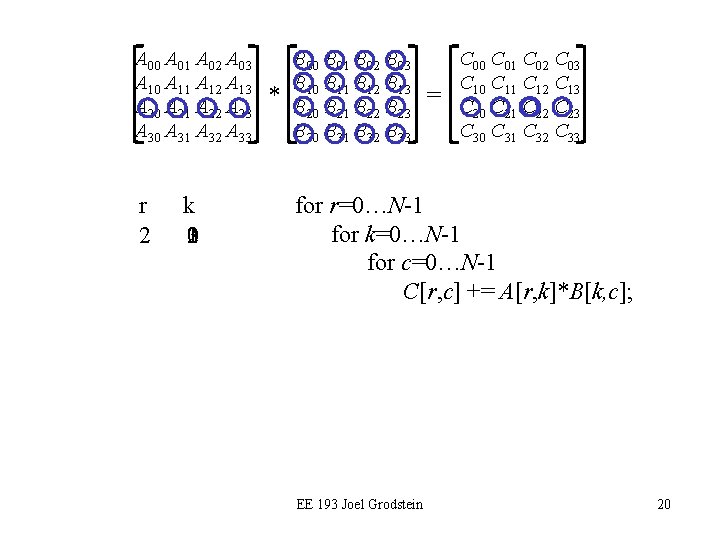
A 00 A 01 A 02 A 03 A 10 A 11 A 12 A 13 A 20 A 21 A 22 A 23 A 30 A 31 A 32 A 33 r 0 k 3210 * B 00 B 01 B 02 B 03 B 10 B 11 B 12 B 13 B 20 B 21 B 22 B 23 B 30 B 31 B 32 B 33 = C 00 C 01 C 02 C 03 C 10 C 11 C 12 C 13 C 20 C 21 C 22 C 23 C 30 C 31 C 32 C 33 for r=0…N-1 for k=0…N-1 for c=0…N-1 C[r, c] += A[r, k]*B[k, c]; EE 193 Joel Grodstein 18

A 00 A 01 A 02 A 03 A 10 A 11 A 12 A 13 A 20 A 21 A 22 A 23 A 30 A 31 A 32 A 33 r 1 k 3210 * B 00 B 01 B 02 B 03 B 10 B 11 B 12 B 13 B 20 B 21 B 22 B 23 B 30 B 31 B 32 B 33 = C 00 C 01 C 02 C 03 C 10 C 11 C 12 C 13 C 20 C 21 C 22 C 23 C 30 C 31 C 32 C 33 for r=0…N-1 for k=0…N-1 for c=0…N-1 C[r, c] += A[r, k]*B[k, c]; EE 193 Joel Grodstein 19

A 00 A 01 A 02 A 03 A 10 A 11 A 12 A 13 A 20 A 21 A 22 A 23 A 30 A 31 A 32 A 33 r 2 k 3210 * B 00 B 01 B 02 B 03 B 10 B 11 B 12 B 13 B 20 B 21 B 22 B 23 B 30 B 31 B 32 B 33 = C 00 C 01 C 02 C 03 C 10 C 11 C 12 C 13 C 20 C 21 C 22 C 23 C 30 C 31 C 32 C 33 for r=0…N-1 for k=0…N-1 for c=0…N-1 C[r, c] += A[r, k]*B[k, c]; EE 193 Joel Grodstein 20

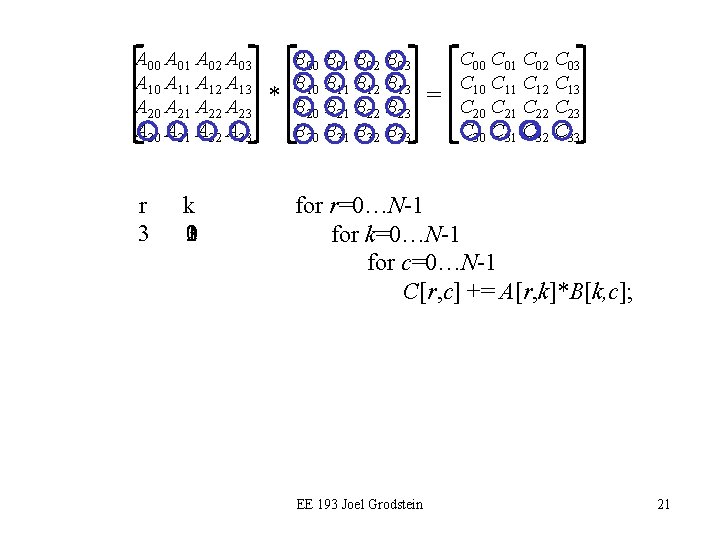
A 00 A 01 A 02 A 03 A 10 A 11 A 12 A 13 A 20 A 21 A 22 A 23 A 30 A 31 A 32 A 33 r 3 k 3210 * B 00 B 01 B 02 B 03 B 10 B 11 B 12 B 13 B 20 B 21 B 22 B 23 B 30 B 31 B 32 B 33 = C 00 C 01 C 02 C 03 C 10 C 11 C 12 C 13 C 20 C 21 C 22 C 23 C 30 C 31 C 32 C 33 for r=0…N-1 for k=0…N-1 for c=0…N-1 C[r, c] += A[r, k]*B[k, c]; EE 193 Joel Grodstein 21

A 00 A 01 A 02 A 03 A 10 A 11 A 12 A 13 A 20 A 21 A 22 A 23 A 30 A 31 A 32 A 33 * B 00 B 01 B 02 B 03 B 10 B 11 B 12 B 13 B 20 B 21 B 22 B 23 B 30 B 31 B 32 B 33 = C 00 C 01 C 02 C 03 C 10 C 11 C 12 C 13 C 20 C 21 C 22 C 23 C 30 C 31 C 32 C 33 for r=0…N-1 for k=0…N-1 for c=0…N-1 C[r, c] += A[r, k]*B[k, c]; • Let's go parallel. Assign each thread to just a few r values. We want to assign each thread to one core, and have each thread only access as much memory as can fit in L 2. Does it work? – Each thread must now access only its own rows of A and C – Each thread still accesses every element of B; and once per value of r. • Conclusion: each thread must be able to hold all of B in its cache. Other than that, it parallelizes quite well. EE 193 Joel Grodstein 22

Block-matrix algorithms • What happens if B doesn't fit into our relevant cache? Is this a real concern? – YES. Matrices can be big…, and we want to be able to do linear algebra on small CPUs (e. g. , for Folding @home)… and GPUs have small caches. • Let's try to change our algorithm to work even on small caches and big matrices. EE 193 Joel Grodstein 23

Baby step • Consider the two programs: for i=0. . 7 do something with i; for a=0. . 1 for b=0. . 3 i=4*a+b; do something with i; • Do they get the same results? – Unless the "do something" is very tricky, yes they do. EE 193 Joel Grodstein 24

Interpretation: matrix blocks A 00 A 01 A 02 A 03 A 10 A 11 A 12 A 13 A 20 A 21 A 22 A 23 A 30 A 31 A 32 A 33 • Break the 4 x 4 matrix into 4 2 x 2 blocks – – Block 0, 0 Block 0, 1 Block 1, 0 Block 1, 1 EE 193 Joel Grodstein 25

A 00 A 01 A 02 A 03 A 10 A 11 A 12 A 13 A 20 A 21 A 22 A 23 A 30 A 31 A 32 A 33 * B 00 B 01 B 02 B 03 B 10 B 11 B 12 B 13 B 20 B 21 B 22 B 23 B 30 B 31 B 32 B 33 = C 00 C 01 C 02 C 03 C 10 C 11 C 12 C 13 C 20 C 21 C 22 C 23 C 30 C 31 C 32 C 33 for rb=0…Nb-1 Pick the row for ri=0. . Ni-1 for kb=0. . Nb-1 Pick k for ki=0. . Ni-1 for cb=0. . Nb-1 Pick the column for ci=0. . Ni-1 r = rb*Ni+ri; k = kb*Ni+ki; c = cb*Ni+ci; C[r, c] += A[r, k]*B[k, c]; • Do we believe that this has the same result as before? – Yes. But it is getting a bit confusing. EE 193 Joel Grodstein 26

A 00 A 01 A 02 A 03 A 10 A 11 A 12 A 13 A 20 A 21 A 22 A 23 A 30 A 31 A 32 A 33 * B 00 B 01 B 02 B 03 B 10 B 11 B 12 B 13 B 20 B 21 B 22 B 23 B 30 B 31 B 32 B 33 = C 00 C 01 C 02 C 03 C 10 C 11 C 12 C 13 C 20 C 21 C 22 C 23 C 30 C 31 C 32 C 33 for rb=0…Nb-1 for ri=0…Ni-1 for kb=0…Nb-1 for ki=0…Ni-1 for cb=0…Nb-1 for ci=0…Ni-1 r = rb*Ni+ri; k = kb*Ni+ki; c = cb*Ni+ci; C[r, c] += A[r, k]*B[k, c]; • Now swap some loops EE 193 Joel Grodstein 27

A 00 A 01 A 02 A 03 A 10 A 11 A 12 A 13 A 20 A 21 A 22 A 23 A 30 A 31 A 32 A 33 * B 00 B 01 B 02 B 03 B 10 B 11 B 12 B 13 B 20 B 21 B 22 B 23 B 30 B 31 B 32 B 33 = C 00 C 01 C 02 C 03 C 10 C 11 C 12 C 13 C 20 C 21 C 22 C 23 C 30 C 31 C 32 C 33 for rb=0…Nb-1 for kb=0. . Nb-1 Pick the block for cb=0. . Nb-1 for ri=0. . Ni-1 Pick the offset for ki=0. . Ni-1 within a block for ci=0. . Ni-1 r = rb*Ni+ri; k = kb*Ni+ki; c = cb*Ni+ci; C[r, c] += A[r, k]*B[k, c]; • What? Doesn't it only take two numbers to specify a block? ? ? EE 193 Joel Grodstein 28

A 00 A 01 A 02 A 03 A 10 A 11 A 12 A 13 A 20 A 21 A 22 A 23 A 30 A 31 A 32 A 33 * B 00 B 01 B 02 B 03 B 10 B 11 B 12 B 13 B 20 B 21 B 22 B 23 B 30 B 31 B 32 B 33 = C 00 C 01 C 02 C 03 C 10 C 11 C 12 C 13 C 20 C 21 C 22 C 23 C 30 C 31 C 32 C 33 for rb=0…Nb-1 rb c b k b for kb=0. . Nb-1 Pick the 0 0 10 for cb=0. . Nb-1 three blocks for ri=0. . Ni-1 for ki=0. . Ni-1 for ci=0. . Ni-1 r = rb*Ni+ri; k = kb*Ni+ki; c = cb*Ni+ci; C[r, c] += A[r, k]*B[k, c]; • Yes, it only take two numbers to specify a block. But A, B and C each use a different index pair. EE 193 Joel Grodstein 29

A 00 A 01 A 02 A 03 A 10 A 11 A 12 A 13 A 20 A 21 A 22 A 23 A 30 A 31 A 32 A 33 * B 00 B 01 B 02 B 03 B 10 B 11 B 12 B 13 B 20 B 21 B 22 B 23 B 30 B 31 B 32 B 33 = C 00 C 01 C 02 C 03 C 10 C 11 C 12 C 13 C 20 C 21 C 22 C 23 C 30 C 31 C 32 C 33 for rb=0…Nb-1 rb c b k b for kb=0. . Nb-1 Pick the block 0 10 1 for cb=0. . Nb-1 for ri=0. . Ni-1 for ki=0. . Ni-1 for ci=0. . Ni-1 r = rb*Ni+ri; k = kb*Ni+ki; c = cb*Ni+ci; C[r, c] += A[r, k]*B[k, c]; • Yes, it only take two numbers to specify a block. But A, B and C each use a different index pair. EE 193 Joel Grodstein 30

A 00 A 01 A 02 A 03 A 10 A 11 A 12 A 13 A 20 A 21 A 22 A 23 A 30 A 31 A 32 A 33 * B 00 B 01 B 02 B 03 B 10 B 11 B 12 B 13 B 20 B 21 B 22 B 23 B 30 B 31 B 32 B 33 = C 00 C 01 C 02 C 03 C 10 C 11 C 12 C 13 C 20 C 21 C 22 C 23 C 30 C 31 C 32 C 33 for rb=0…Nb-1 rb c b k b for kb=0. . Nb-1 Pick the block 10 01 1 for cb=0. . Nb-1 for ri=0. . Ni-1 for ki=0. . Ni-1 for ci=0. . Ni-1 r = rb*Ni+ri; k = kb*Ni+ki; c = cb*Ni+ci; C[r, c] += A[r, k]*B[k, c]; • Yes, it only take two numbers to specify a block. But A, B and C each use a different index pair. EE 193 Joel Grodstein 31

A 00 A 01 A 02 A 03 A 10 A 11 A 12 A 13 A 20 A 21 A 22 A 23 A 30 A 31 A 32 A 33 * B 00 B 01 B 02 B 03 B 10 B 11 B 12 B 13 B 20 B 21 B 22 B 23 B 30 B 31 B 32 B 33 = C 00 C 01 C 02 C 03 C 10 C 11 C 12 C 13 C 20 C 21 C 22 C 23 C 30 C 31 C 32 C 33 for each triplet of three blocks specified by rb, cb, kb for each element combination ri, ci, ki within the blocks r = rb*Ni+ri; k = kb*Ni+ki; c = cb*Ni+ci; C[r, c] += A[r, k]*B[k, c]; • EE 193 Joel Grodstein 32

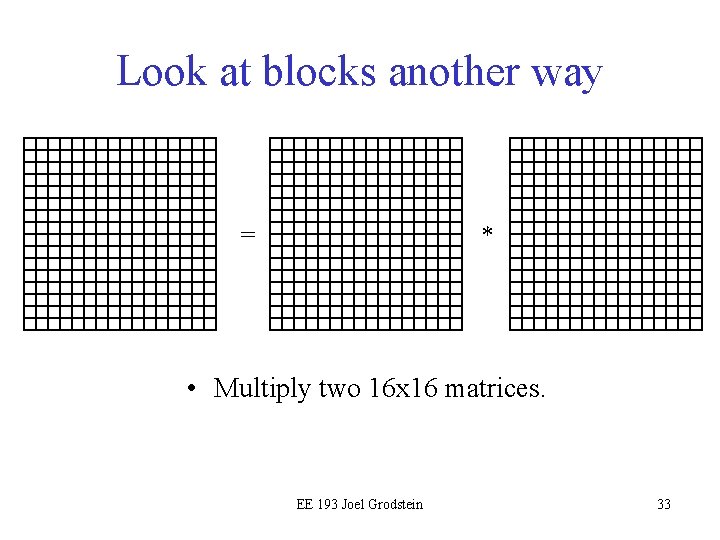
Look at blocks another way = * • Multiply two 16 x 16 matrices. EE 193 Joel Grodstein 33

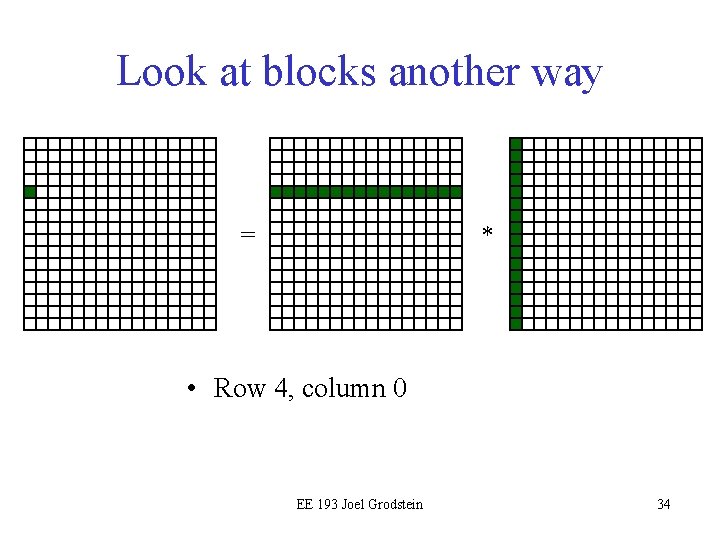
Look at blocks another way = * • Row 4, column 0 EE 193 Joel Grodstein 34

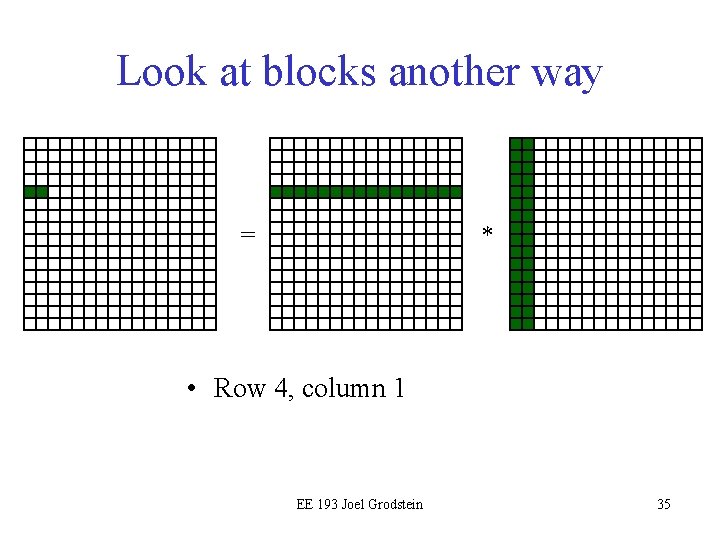
Look at blocks another way = * • Row 4, column 1 EE 193 Joel Grodstein 35

Look at blocks another way = * • Row 5, column 0 EE 193 Joel Grodstein 36

Look at blocks another way = * • Block 1, 0 EE 193 Joel Grodstein 37

Look at blocks another way = * • Interpretation: block[1, 0] = row[1] ∙ column[0] • The output block depends only on the input blocks. • We reused the same rows/columns over & over. EE 193 Joel Grodstein 38

Block-matrix and threads • We have a block-matrix algorithm – We even understand it – It should make good use of caches, and thus be quite fast. • Next problems: – ordering the inner and outer loops – multithreading • Simplifying assumption: – Pick the block size so that it fits into the L 2 (or lower) cache – Use the L 3 (i. e. , ring cache) to get “some” reuse of blocks without going to main memory EE 193 Joel Grodstein 39

for rb=0…Nb-1 for kb=0. . Nb-1 for cb=0. . Nb-1 for ri=0. . Ni-1 Pick the offset for ki=0. . Ni-1 within a block for ci=0. . Ni-1 r = rb*Ni+ri; k = kb*Ni+ki; c = cb*Ni+ci; C[r, c] += A[r, k]*B[k, c]; • Does it matter what order we put the three inner loops? After all, blocks fit into the L 2. – Probably. It would be nice to get a lot of hits from the L 1, to make sure our cores don’t wait for memory EE 193 Joel Grodstein 40

for rb=0…Nb-1 for kb=0. . Nb-1 Pick the block for cb=0. . Nb-1 for ri=0. . Ni-1 for ki=0. . Ni-1 for ci=0. . Ni-1 r = rb*Ni+ri; k = kb*Ni+ki; c = cb*Ni+ci; C[r, c] += A[r, k]*B[k, c]; • Does it matter what order we put the three outer loops? After all, there’s enough computation that the initial blockloading time doesn’t matter. – Perhaps. But that depends on a lot of factors, and it’s easy enough to pick a good loop ordering. That will let us reload blocks from the L 3 rather than from main memory. – What order to use? – rb/kb/cb looks good, for the same reasons as before. EE 193 Joel Grodstein 41

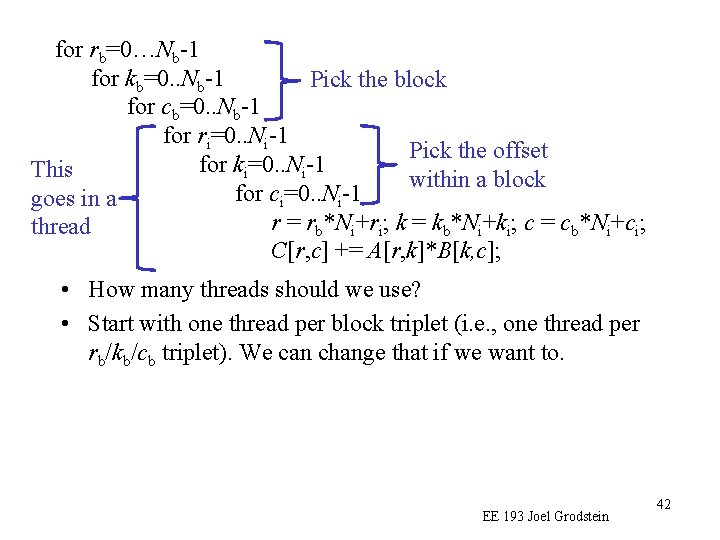
for rb=0…Nb-1 for kb=0. . Nb-1 Pick the block for cb=0. . Nb-1 for ri=0. . Ni-1 Pick the offset for k =0. . N -1 This i i within a block for ci=0. . Ni-1 goes in a r = rb*Ni+ri; k = kb*Ni+ki; c = cb*Ni+ci; thread C[r, c] += A[r, k]*B[k, c]; • How many threads should we use? • Start with one thread per block triplet (i. e. , one thread per rb/kb/cb triplet). We can change that if we want to. EE 193 Joel Grodstein 42

for rb=0…Nb-1 for kb=0. . Nb-1 Pick the block for cb=0. . Nb-1 for ri=0. . N thread (thread_func, rb, kb. Pick , cb); the offset i-1 for ki=0. . Ni-1 This within a block for ci=0. . Ni-1 goes in a r = rb*Ni+ri; k = kb*Ni+ki; c = cb*Ni+ci; thread C[r, c] += A[r, k]*B[k, c]; • Start with one thread per block triplet (i. e. , one thread per rb/kb/cb triplet). • How many threads are there? Nb 3 • If we have 1 Kx 1 K matrices, and 64 x 64 blocks, then how many threads are there? – 1 K/64 = 16. So Nb=16, and there are 163=4 K threads • What do you think about the code above? – Way too many threads to launch all at once! EE 193 Joel Grodstein 43

for rb=0…Nb-1 for kb=0. . Nb-1 Pick the block for cb=0. . Nb-1 thread (thread_func, rb, kb, cb); • Another issue: do we need a critical section to avoid multiple threads writing the same data values? – Yes. Every thread with the same rb and cb all try to write the same locations of the output matrix. • How many threads are fighting each other? – Nb (i. e. , all the different values of kb) • If we use a critical section to protect the “C[r, c] += A[r, k]*B[k, c]”, how will that affect performance? – Basically, no two threads can run at the same time any more • If we make each thread keep its own private work area and then merge them, how will that work? – Each thread will need to keep an entire block as its own work space. That’s potentially a lot of space. And the merging is (#threads)*Nb 2 flops, which is non-trivial EE 193 Joel Grodstein 44

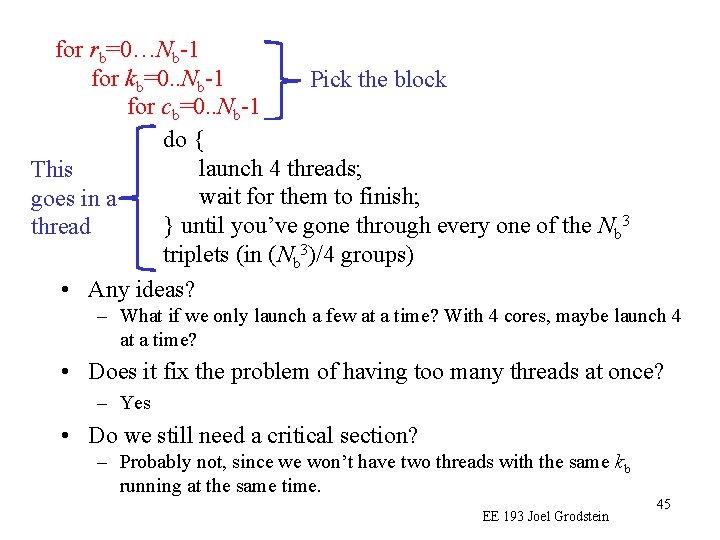
for rb=0…Nb-1 for kb=0. . Nb-1 Pick the block for cb=0. . Nb-1 for {ri=0. . Ni-1 do Pick the offset for k =0. . N -1 launch This i 4 threads; i within a block =0. . Nto waitfor forcithem goes in a i-1 finish; 3 ; r = gone rb*Ni+r = cthe } until you’ve through one Ni+c thread i; k = kevery b*Ni+k i; c of b*N b i 3 C[r, c] += A[r, k]*B[k, c]; triplets (in (N b )/4 groups) • Any ideas? – What if we only launch a few at a time? With 4 cores, maybe launch 4 at a time? • Does it fix the problem of having too many threads at once? – Yes • Do we still need a critical section? – Probably not, since we won’t have two threads with the same kb running at the same time. EE 193 Joel Grodstein 45

Results on Norbert for kb=0…Nb-1 Launching a thread takes for rb=0. . Nb-1. 01 ms, so. 3 s total for cb=0. . Nb-1 Spawn a thread to compute C[r, c] += A[r, k]*B[k, c]; (for every ri, ci, ki in the three blocks) if (we've spawned as many threads as cores) wait for them all to finish; • Very slow. Why? • Another problem, too. – – 1 Kx 1 K matrices, 64 x 64 blocks → Nb=32. How many threads? 32 x 32=32 K How many groups of 32 threads (there are 32 cores)? 1024 Different threads go at different rates. We have 1024 iterations of "wait for the slowest thread to finish. " Hugely inefficient. 46 EE 193 Joel Grodstein

What to do? for kb=0…Nb-1 for rb=0. . Nb-1 for cb=0. . Nb-1 Spawn a thread to compute C[r, c] += A[r, k]*B[k, c]; (for every r, c, k in the three blocks) if (we've spawned as many threads as cores) wait for them all to finish; • What are your thoughts on how to fix this? – We launched too many threads – We kept having the fastest thread wait for the slowest • You get to take your best shot in HW #3. – But you can brainstorm together here first EE 193 Joel Grodstein 47

Brainstorming • Brainstorm ideas and write some metacode on the board • Questions to ask: – you don’t want to launch a million threads. Roughly how many threads do you want to launch? – Can you divide up the work between threads so that you don’t need a critical section? – You must initialize the output matrix to 0 before threads start summing partial products into it. Can you distribute this work among threads also? EE 193 Joel Grodstein 48

SMT • Onto the next problem • We've assumed 1 thread/core until now. Any problem with that? – SMT is often a good thing. It allows one thread to compute while the other thread is stalled anyway. – If we write the 1 st thread really well, perhaps it will never stall anyway? • Let's try to use hyperthreading. – Can we spawn 2 threads/core instead of 1? EE 193 Joel Grodstein 49

C++ threads can really suck • Let's say we divvy up the work on a block triplet among two threads in the same core • But wait – we have a big problem – C++ threads does not let you assign threads to cores. It lets the O/S do its best – There’s no guarantee our two threads, using the same block triplet, will be assigned to the same core. – In fact, even if we only have 1 thread/core, a stupid enough O/S might put all the threads on 1 core. EE 193 Joel Grodstein 50

What to do about it • An interesting final project would be to see how well the O/S does, or see how much better you can do yourself. • There are low-level routines (mostly O/S dependent) that let you – find out where threads went – assign threads to cores. – See http: //eli. thegreenplace. net/2016/c 11 -threadsaffinity-and-hyperthreading/ EE 193 Joel Grodstein 51