EE 121 John Wakerly Lecture 6 Adders Multipliers

EE 121 John Wakerly Lecture #6 Adders Multipliers Read-Only Memories Barrel-Shifter Design Example 1

Equality Comparators • 1 -bit comparator • 4 -bit comparator EQ_L 2

8 -bit Magnitude Comparator 3

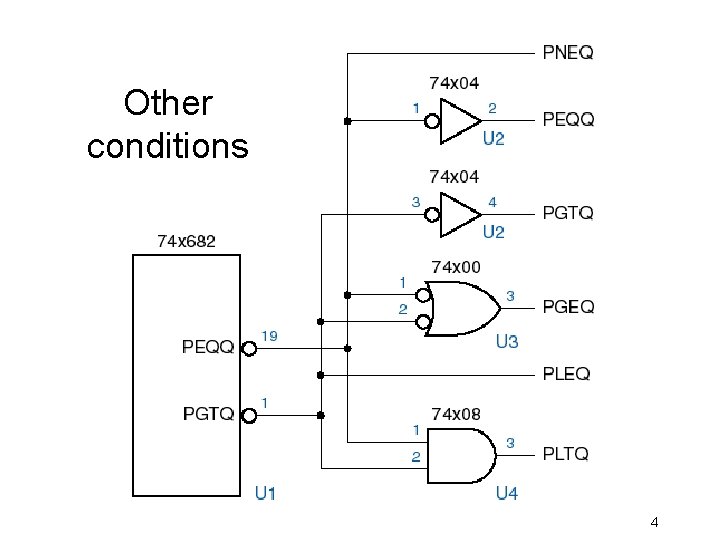
Other conditions 4

Comparators in ABEL • Equality checking – PEQQ = ([P 7. . P 0] == [Q 7. . Q 0]); – PEQQ_L = !([P 7. . P 0] == [Q 7. . Q 0]); – 16 product terms • Magnitude comparison – PGTQ = ([P 7. . P 0] > [Q 7. . Q 0]); – PGTQ_L = !([P 7. . P 0] > [Q 7. . Q 0]); – 255 product terms (try it in Foundation!) 5

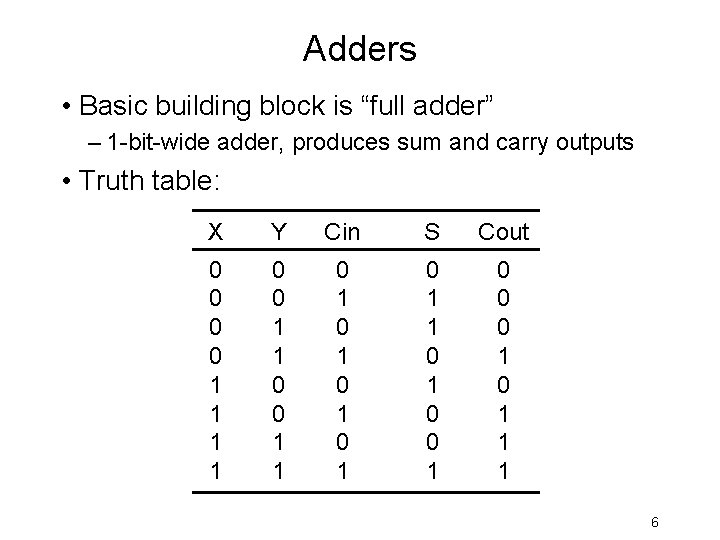
Adders • Basic building block is “full adder” – 1 -bit-wide adder, produces sum and carry outputs • Truth table: X Y Cin S Cout 0 0 1 1 0 1 0 1 0 1 1 0 0 0 1 1 1 6

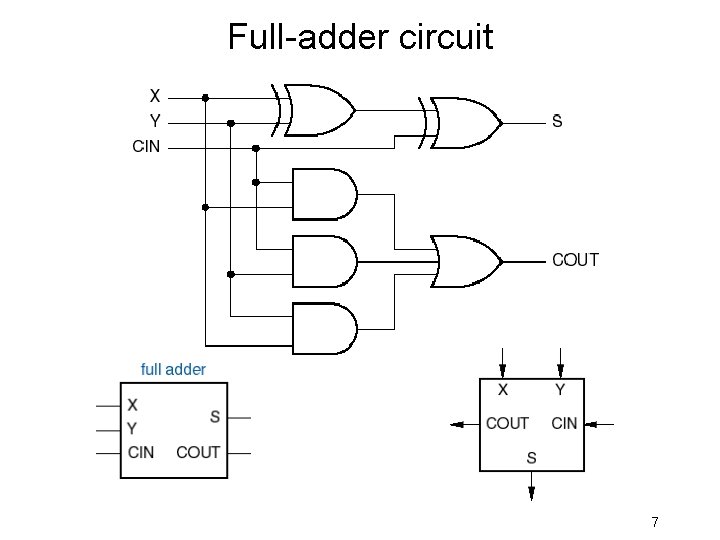
Full-adder circuit 7

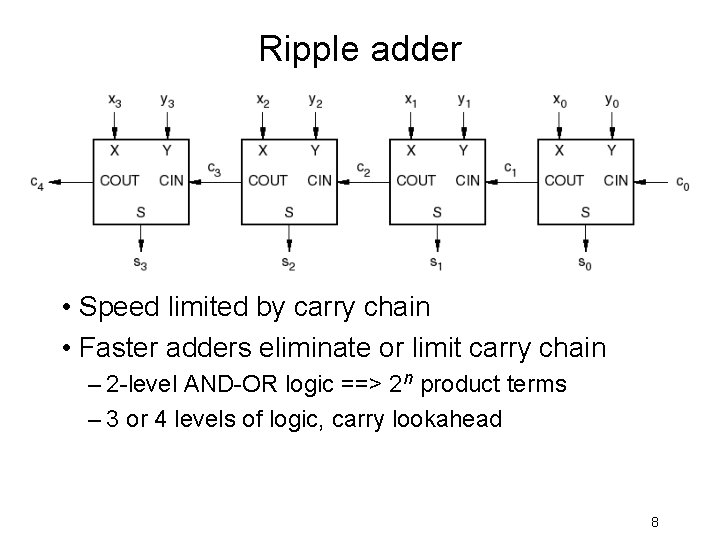
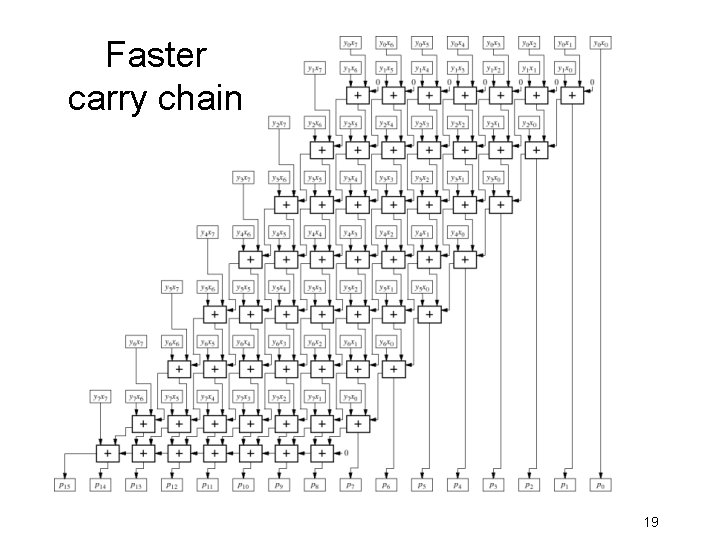
Ripple adder • Speed limited by carry chain • Faster adders eliminate or limit carry chain – 2 -level AND-OR logic ==> 2 n product terms – 3 or 4 levels of logic, carry lookahead 8

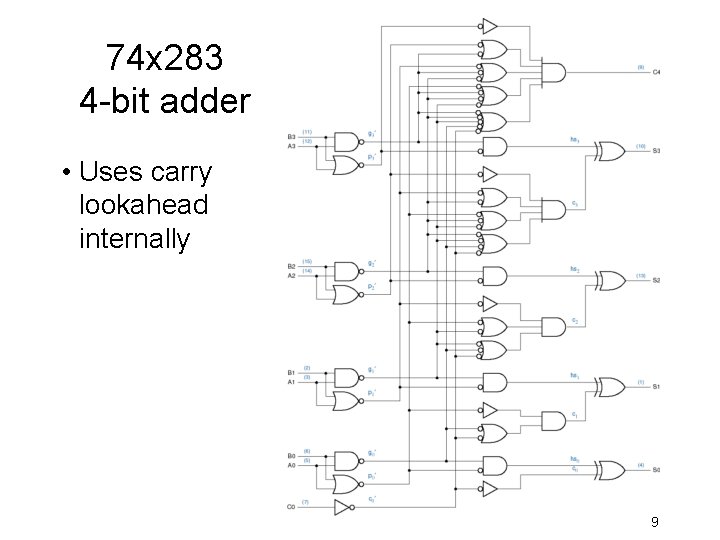
74 x 283 4 -bit adder • Uses carry lookahead internally 9

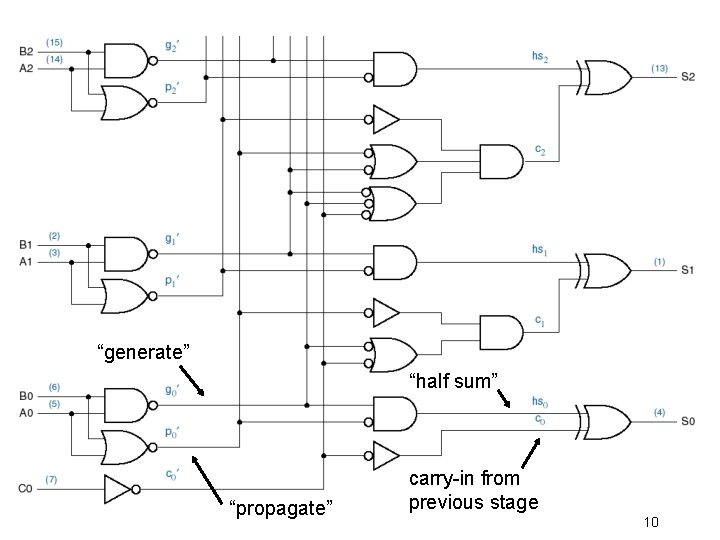
“generate” “half sum” “propagate” carry-in from previous stage 10

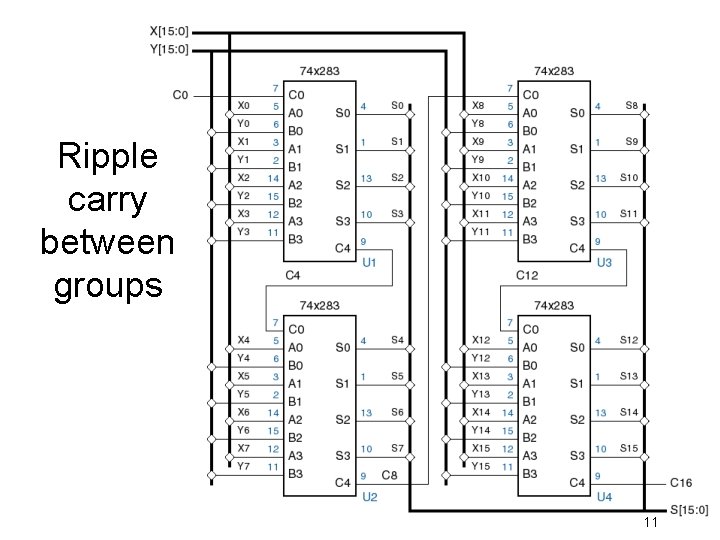
Ripple carry between groups 11

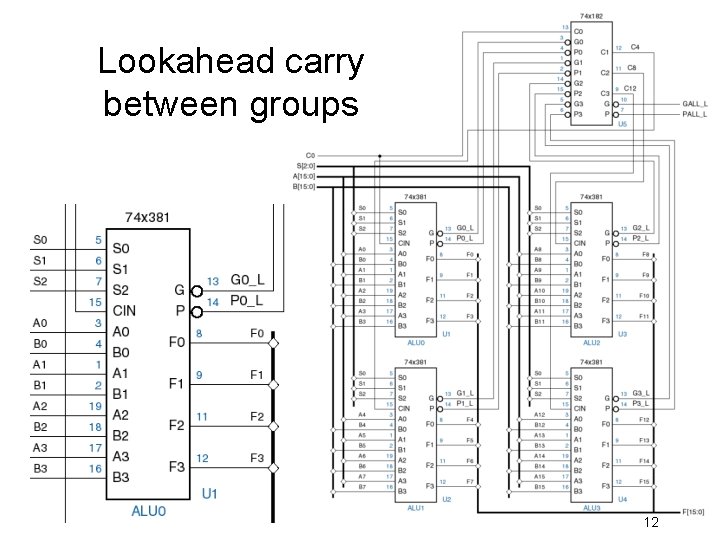
Lookahead carry between groups 12

Addition in ABEL • Easy? – No -- huge number of product terms! – On the order of 2 n for bit n – @CARRY directive 13

Subtraction • Subtraction is the same as addition of the two’s complement. • The two’s complement is the bit-by-bit complement plus 1. • Therefore, X – Y = X + Y + 1. – Complement Y inputs to adder, set Cin to 1. – For a borrow, set Cin to 0. 14

Full subtractor = full adder, almost 15

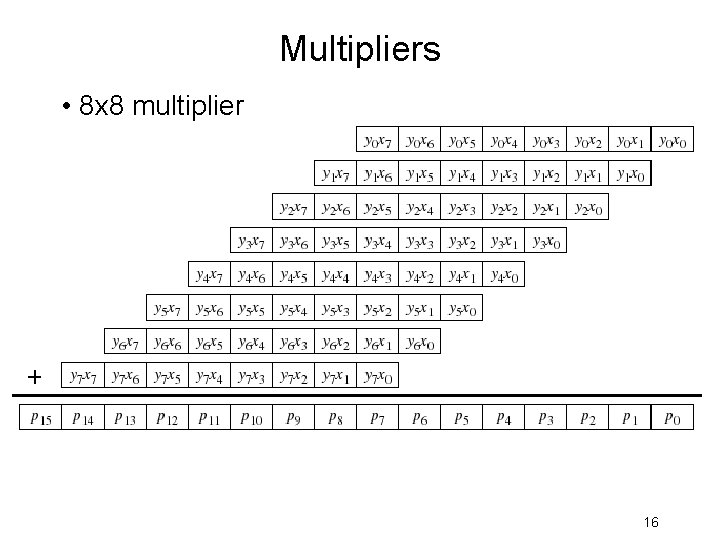
Multipliers • 8 x 8 multiplier 16

4 x 4 multiplier in ABEL 17

Full-adder array 18

Faster carry chain 19

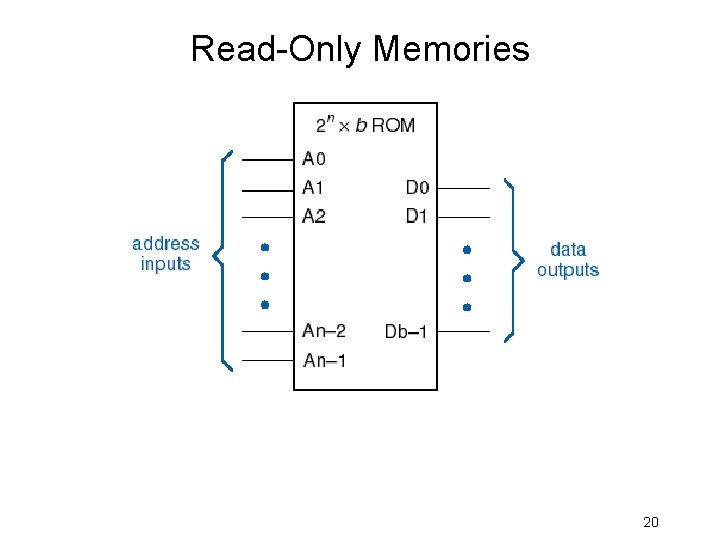
Read-Only Memories 20

Why “ROM”? • Program storage – Boot ROM for personal computers – Complete application storage for embedded systems. • Actually, a ROM is a combinational circuit, basically a truth-table lookup. – Can perform any combinational logic function – Address inputs = function inputs – Data outputs = function outputs 21

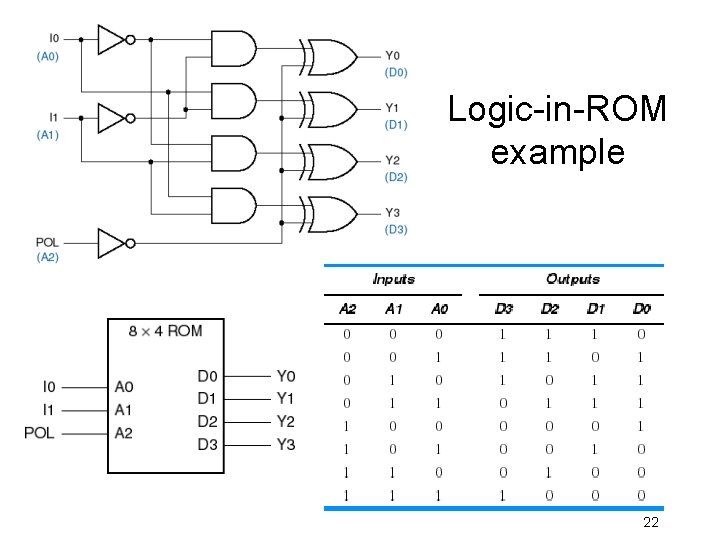
Logic-in-ROM example 22

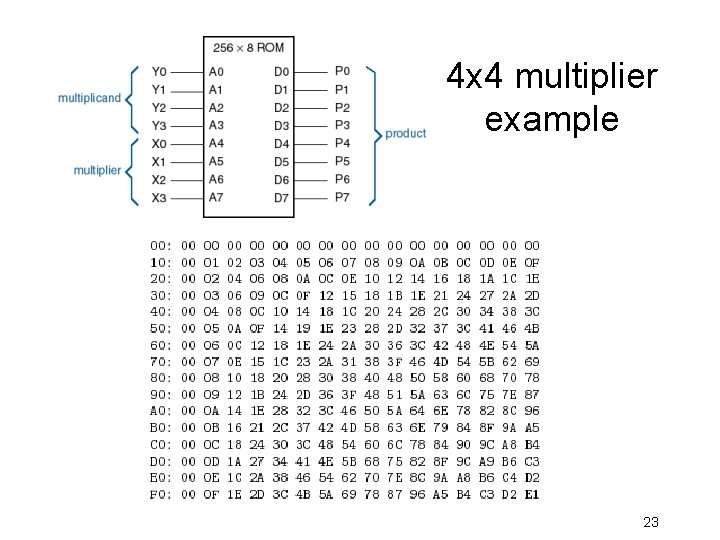
4 x 4 multiplier example 23

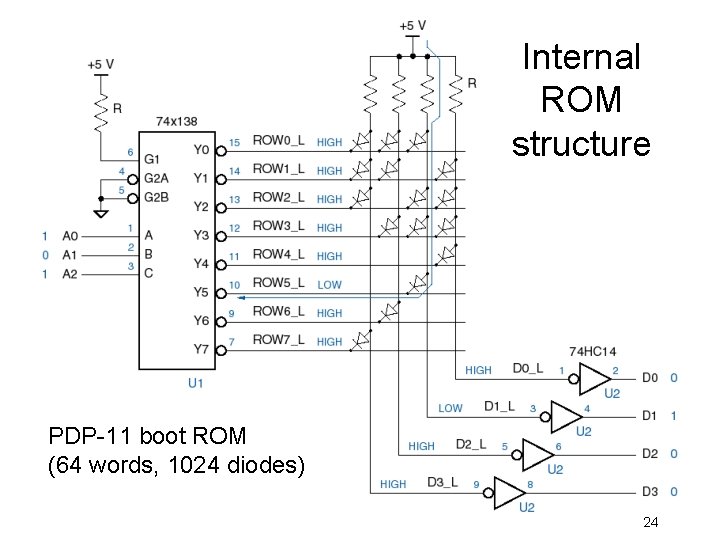
Internal ROM structure PDP-11 boot ROM (64 words, 1024 diodes) 24

Two-dimensional decoding ? 25

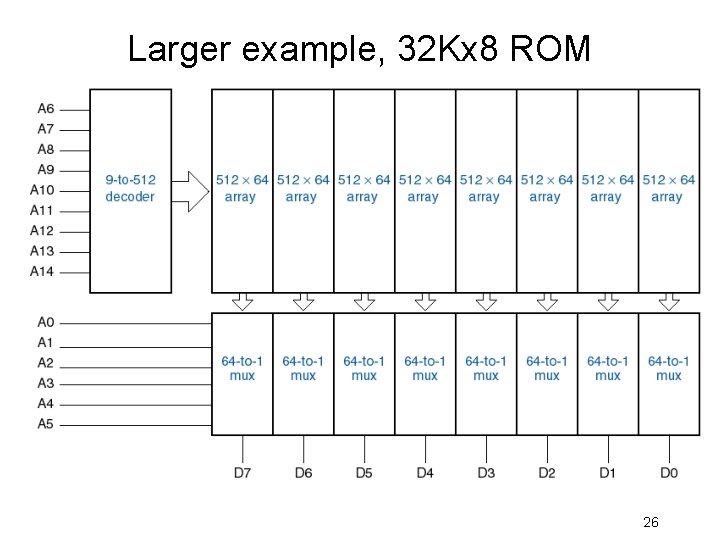
Larger example, 32 Kx 8 ROM 26

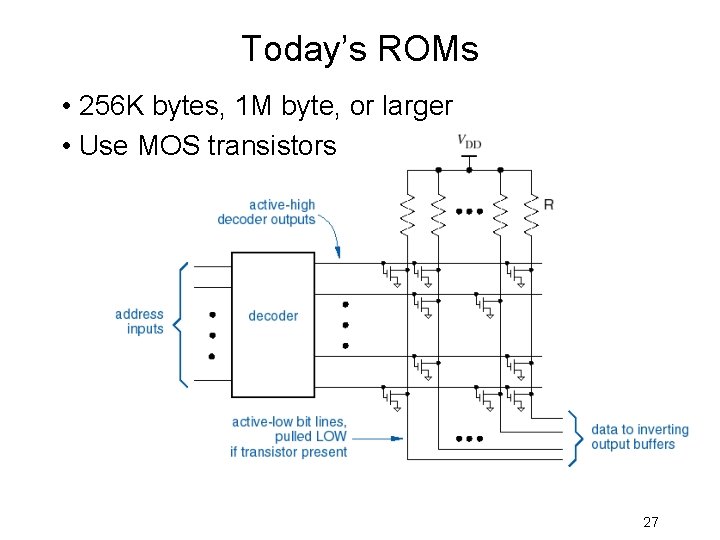
Today’s ROMs • 256 K bytes, 1 M byte, or larger • Use MOS transistors 27

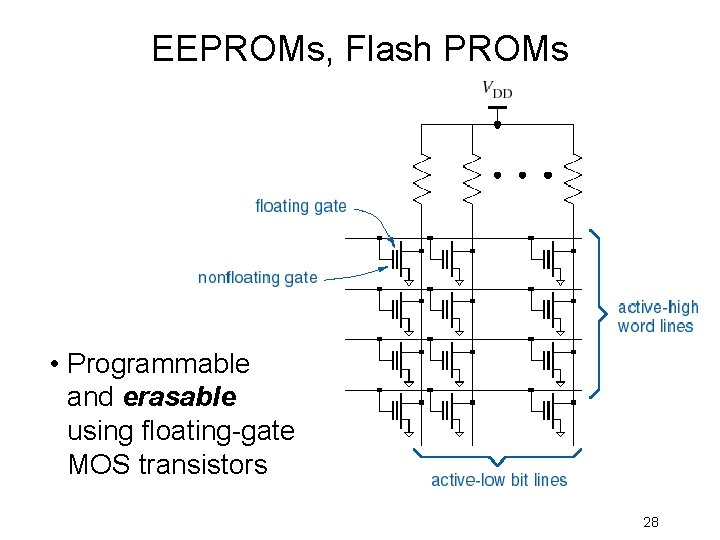
EEPROMs, Flash PROMs • Programmable and erasable using floating-gate MOS transistors 28

Typical commercial EEPROMs 29

EEPROM programming • Apply a higher voltage to force bit change – E. g. , VPP = 12 V – On-chip high-voltage “charge pump” in newer chips • Erase bits – Byte-byte – Entire chip (“flash”) – One block (typically 32 K - 66 K bytes) at a time • Programming and erasing are a lot slower than reading (milliseconds vs. 10’s of nanoseconds) 30

Microprocessor EPROM application 31

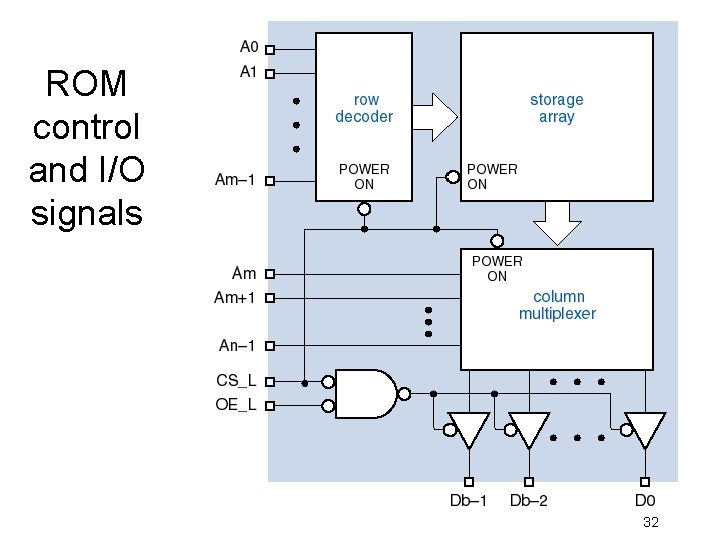
ROM control and I/O signals 32

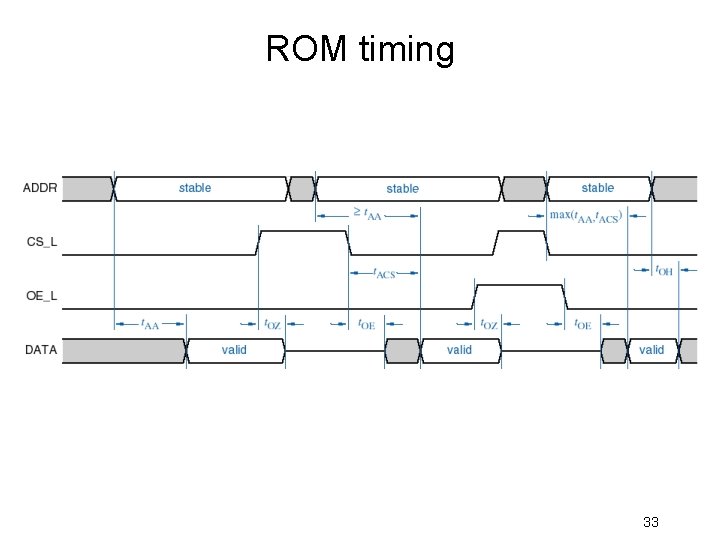
ROM timing 33

Next time • Sequential circuits (Chapter 7) 34