Educational Statistics Response Variable Correlation 10 9 8
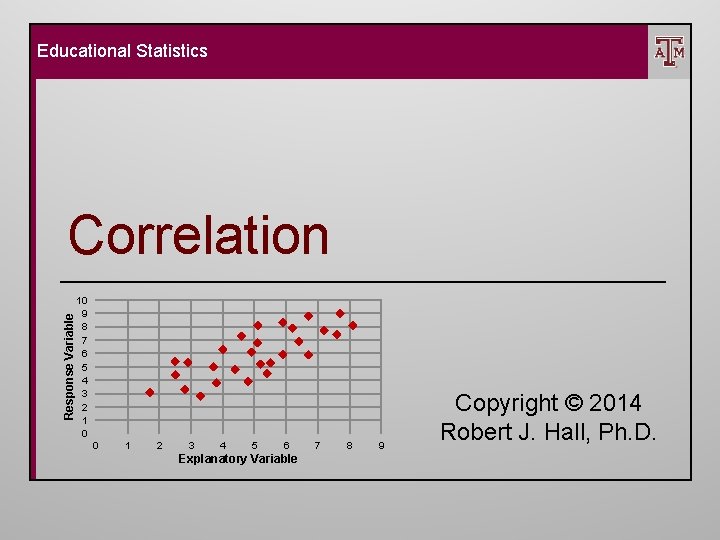
Educational Statistics Response Variable Correlation 10 9 8 7 6 5 4 3 2 1 0 0 1 2 3 4 5 6 Explanatory Variable 7 8 9 Copyright © 2014 Robert J. Hall, Ph. D.

Educational Statistics Topics o Measure of Relationship n n o o o Strength Direction Scatterplot Conceptual Formula Computational Formula Assumptions Problems Effecting the Interpretation of the Correlation Coefficient

Educational Statistics Measure of Relationship o o In a correlational study, two measures -representing the variables of interest -are given to one group of subjects. The subject’s scores on both measures are summarized, and the relationship between the scores on the two measures is examined.

Educational Statistics Measure of Relationship o When the correlation coefficient is used to describe a linear relationship, the coefficient can take on values from -1. 00 to +1. 00. n The sign of the correlation indicates the direction of the relationship between two variables.

Educational Statistics Measure of Relationship o o n A positive relationship means that low scores on X go with low scores on Y whereas high scores on X go with high scores on Y. A negative relationship means that as scores on X increase, scores on Y decrease. The absolute magnitude or size of the correlation coefficient -- that is, ignoring the plus or minus sign -- indicates the strength of the relationship between X and Y.

Educational Statistics Measure of Relationship o o n A correlation of +. 95 or of -. 95 indicates a very strong relationship between the two variables. A correlation of 0 indicates that there is no linear relationship between the variables. Guilford's suggested interpretations for values of r. r xy Value Interpretation Less than. 20 Slight; almost negligible relationship . 20 -. 40 Low correlation; definite but small relationship . 40 -. 70 Moderate correlation; substantial relationship . 70 -. 90 High correlation; marked relationship . 90 - 1. 00 Very high correlation; very dependable relationship
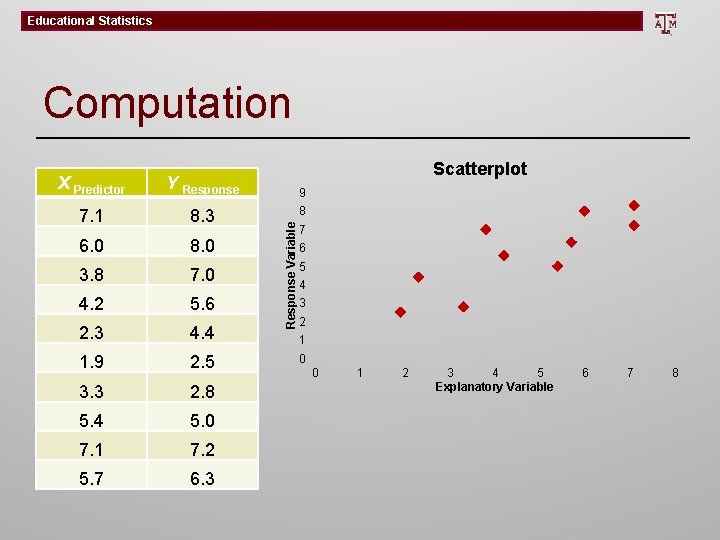
Educational Statistics Computation Y Response 7. 1 8. 3 6. 0 8. 0 3. 8 7. 0 4. 2 5. 6 2. 3 4. 4 1. 9 2. 5 3. 3 2. 8 5. 4 5. 0 7. 1 7. 2 5. 7 6. 3 9 8 Response Variable X Predictor Scatterplot 7 6 5 4 3 2 1 0 0 1 2 3 4 5 Explanatory Variable 6 7 8

Educational Statistics Conceptual / Computational Formulas
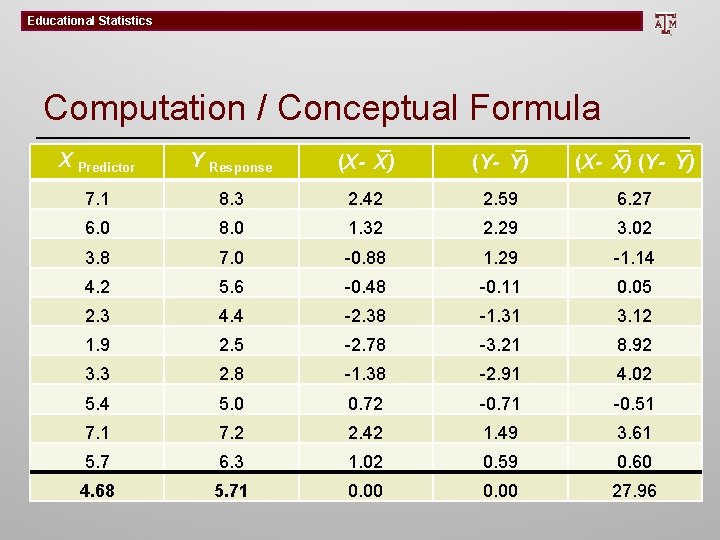
Educational Statistics Computation / Conceptual Formula X Predictor Y Response (X-`X) (Y-`Y) 7. 1 8. 3 2. 42 2. 59 6. 27 6. 0 8. 0 1. 32 2. 29 3. 02 3. 8 7. 0 -0. 88 1. 29 -1. 14 4. 2 5. 6 -0. 48 -0. 11 0. 05 2. 3 4. 4 -2. 38 -1. 31 3. 12 1. 9 2. 5 -2. 78 -3. 21 8. 92 3. 3 2. 8 -1. 38 -2. 91 4. 02 5. 4 5. 0 0. 72 -0. 71 -0. 51 7. 2 2. 42 1. 49 3. 61 5. 7 6. 3 1. 02 0. 59 0. 60 4. 68 5. 71 0. 00 27. 96

Educational Statistics Conceptual Formula
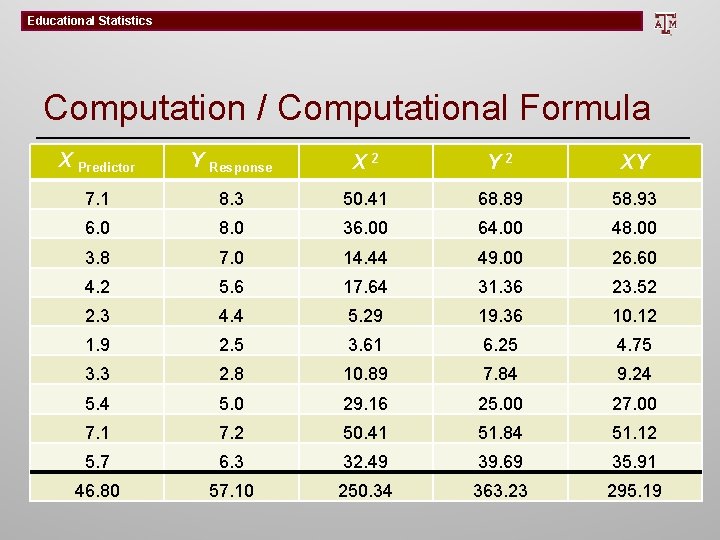
Educational Statistics Computation / Computational Formula X Predictor Y Response X 2 Y 2 XY 7. 1 8. 3 50. 41 68. 89 58. 93 6. 0 8. 0 36. 00 64. 00 48. 00 3. 8 7. 0 14. 44 49. 00 26. 60 4. 2 5. 6 17. 64 31. 36 23. 52 2. 3 4. 4 5. 29 19. 36 10. 12 1. 9 2. 5 3. 61 6. 25 4. 75 3. 3 2. 8 10. 89 7. 84 9. 24 5. 0 29. 16 25. 00 27. 00 7. 1 7. 2 50. 41 51. 84 51. 12 5. 7 6. 3 32. 49 39. 69 35. 91 46. 80 57. 10 250. 34 363. 23 295. 19

Educational Statistics Computational Formula
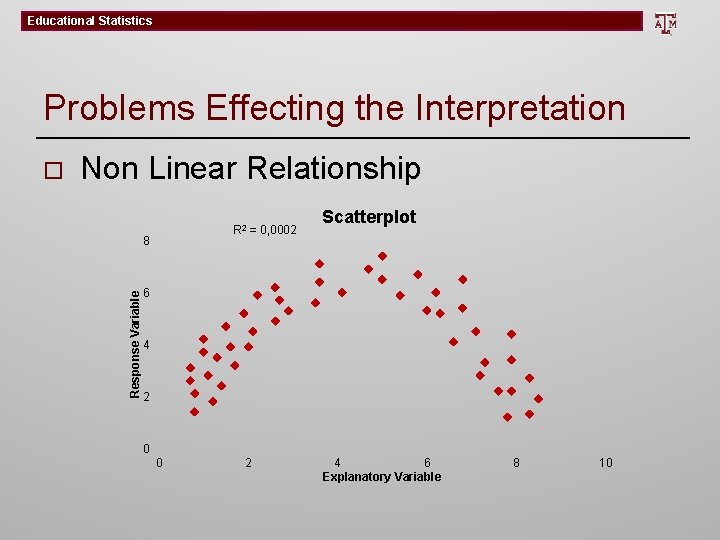
Educational Statistics Problems Effecting the Interpretation Non Linear Relationship R 2 = 0, 0002 8 Response Variable o Scatterplot 6 4 2 0 0 2 4 6 Explanatory Variable 8 10
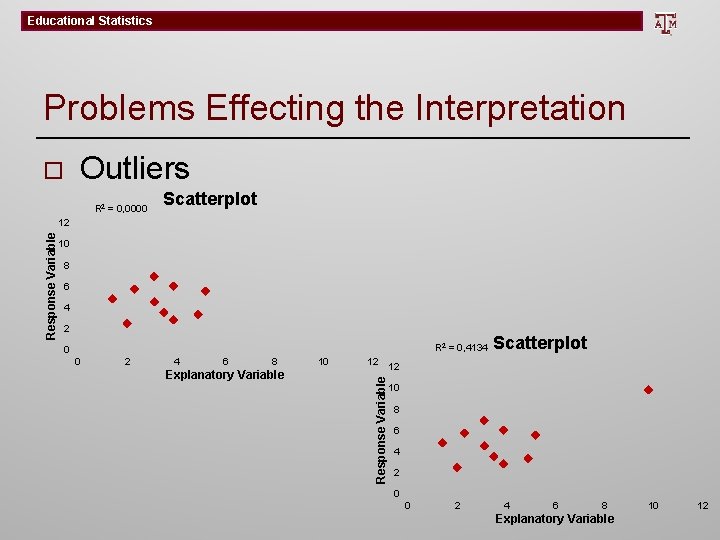
Educational Statistics Problems Effecting the Interpretation Outliers o R 2 = 0, 0000 Scatterplot 10 8 6 4 2 R 2 = 0, 4134 0 0 2 4 6 8 Explanatory Variable 10 12 Response Variable 12 Scatterplot 12 10 8 6 4 2 0 0 2 4 6 8 Explanatory Variable 10 12
- Slides: 14