Educational data mining overview Introduction to Exploratory Data

Educational data mining overview & Introduction to Exploratory Data Analysis with Data. Shop Ken Koedinger CMU Director of PSLC Professor of Human-Computer Interaction & Psychology Carnegie Mellon University

Overview n Data. Shop Overview q q n Quantitative models of learning curves q q n n Logging model Data. Shop Features Power law, logistic regression Contrasting KC models Exploratory Data Analysis Exercise (start) Knowledge Component Model Editing

Logging & Storage Models n Education technologies are “instrumented” to produce log data n We encourage a standard log format q q XML format generalized from Ritter & Koedinger (1995) Also convert log data from other formats

Relational Database -- complex!

Example activity generating “click stream” data n Geometry Cognitive Tutor: “Making Cans” problem q q n Tutor provides feedback & instruction q n Find the area of scrap metal left over after removing a circular area (the end of a can) from a metal square. Student enters values in worksheet Records student’s actions & tutor responses Logs stored in files on school server or database at Carnegie Learning q Later imported into Data. Shop

Data. Shop logging model n Main constructs: q q q Context message: the student, problem, and session with the tutor Tool message: represents an action in the tool performed by a student or tutor Tutor message: represents a tutor’s response to a student action

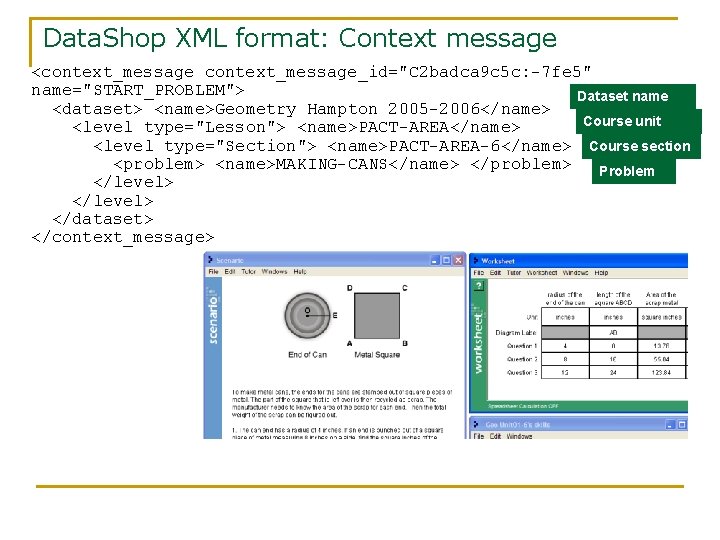
Data. Shop XML format: Context message <context_message_id="C 2 badca 9 c 5 c: -7 fe 5" name="START_PROBLEM"> Dataset name <dataset> <name>Geometry Hampton 2005 -2006</name> Course unit <level type="Lesson"> <name>PACT-AREA</name> <level type="Section"> <name>PACT-AREA-6</name> Course section <problem> <name>MAKING-CANS</name> </problem> Problem </level> </dataset> </context_message>

Data. Shop XML format: Tool & Tutor Messages <tool_message context_message_id="C 2 badca 9 c 5 c: -7 fe 5"> <semantic_event transaction_id="T 2 a 9 c 5 c: -7 fe 7" name="ATTEMPT" /> <event_descriptor> <selection>(POG-AREA QUESTION 2)</selection> <action>INPUT-CELL-VALUE</action> <input>200. 96</input> </event_descriptor> </tool_message> <tutor_message context_message_id="C 2 badca 9 c 5 c: -7 fe 5"> <semantic_event transaction_id="T 2 a 9 c 5 c: -7 fe 7" name="RESULT" /> <event_descriptor> … [as above] … </event_descriptor> <action_evaluation>CORRECT</action_evaluation> </tutor_message>

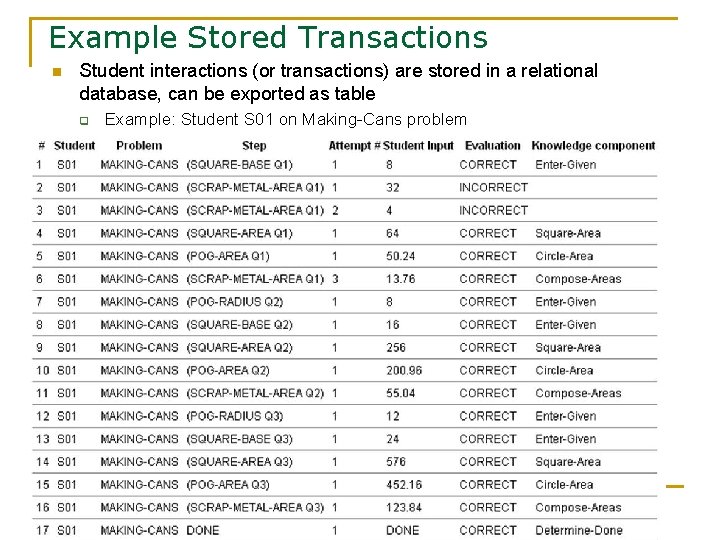
Example Stored Transactions n Student interactions (or transactions) are stored in a relational database, can be exported as table q Example: Student S 01 on Making-Cans problem

Transactions n Info for each transaction q q n student(s), session, time, problem step, attempt number, student action tutor response, number of hints, knowledge component code Logging of on-line tools (e. g. , a virtual lab) does not include tutor response

Step & Transaction Definitions n n n A problem-solving activity typically involves many tool & tutor messages. “Steps” represent completion of possible subgoals or pieces of a problem solution “Transactions” are attempts at a step or requests for instructional help

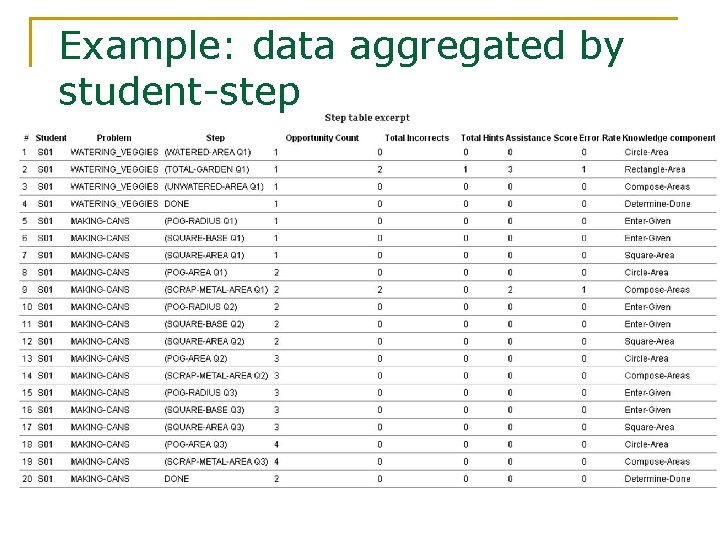
Example: data aggregated by student-step

Overview n Data. Shop Overview q q n Quantitative models of learning curves q q n n Logging model Data. Shop Features Power law, logistic regression Contrasting KC models Exploratory Data Analysis Exercise (start) Knowledge Component Model Editing

Data. Shop Analysis Tools n n n Dataset Info Performance Profiler Learning Curve Error Report Export Sample Selector

Dataset Info • • Papers and Files storage Meta data for given dataset PI’s get ‘edit’ privileges, others must request it Problem Breakdown table Dataset Metrics 15

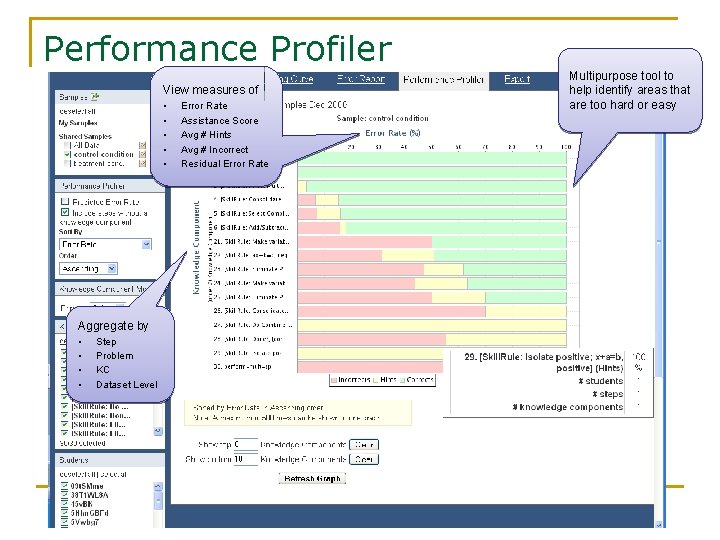
Performance Profiler View measures of • • • Aggregate by • • Step Problem KC Dataset Level Error Rate Assistance Score Avg # Hints Avg # Incorrect Residual Error Rate Multipurpose tool to help identify areas that are too hard or easy

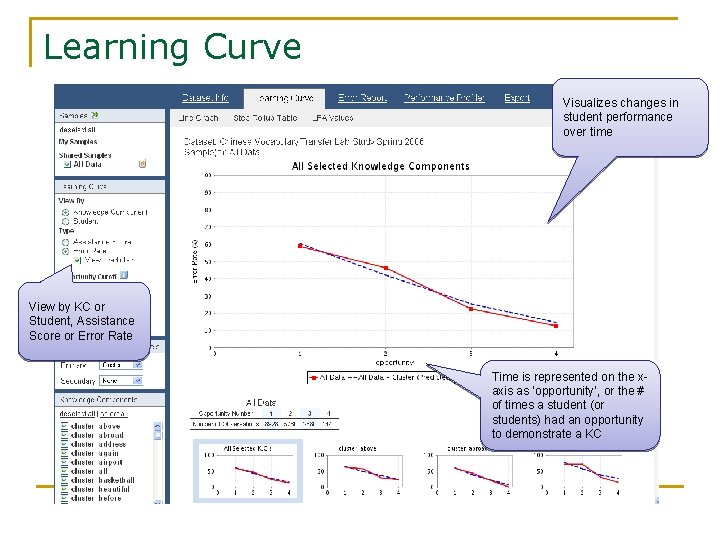
Learning Curve Visualizes changes in student performance over time View by KC or Student, Assistance Score or Error Rate Time is represented on the xaxis as ‘opportunity’, or the # of times a student (or students) had an opportunity to demonstrate a KC

Error Report • • View by Problem or KC Provides a breakdown of problem information (by step) for finegrained analysis of problem-solving behavior Attempts are categorized by student

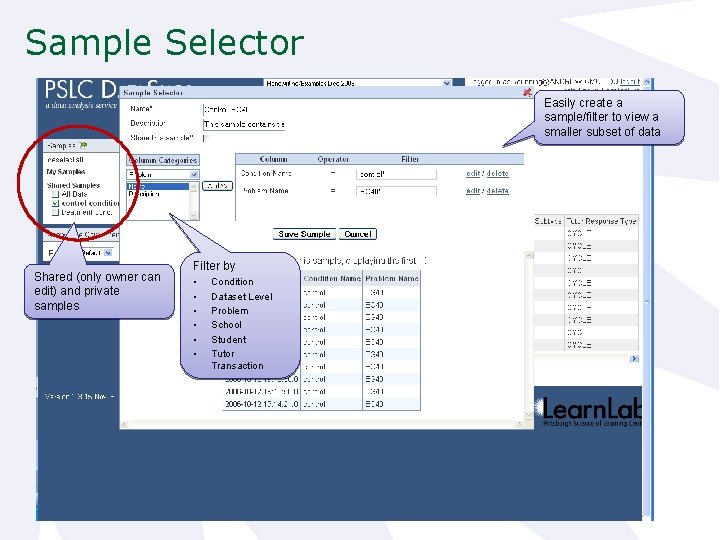
Sample Selector Easily create a sample/filter to view a smaller subset of data Shared (only owner can edit) and private samples Filter by • • • Condition Dataset Level Problem School Student Tutor Transaction

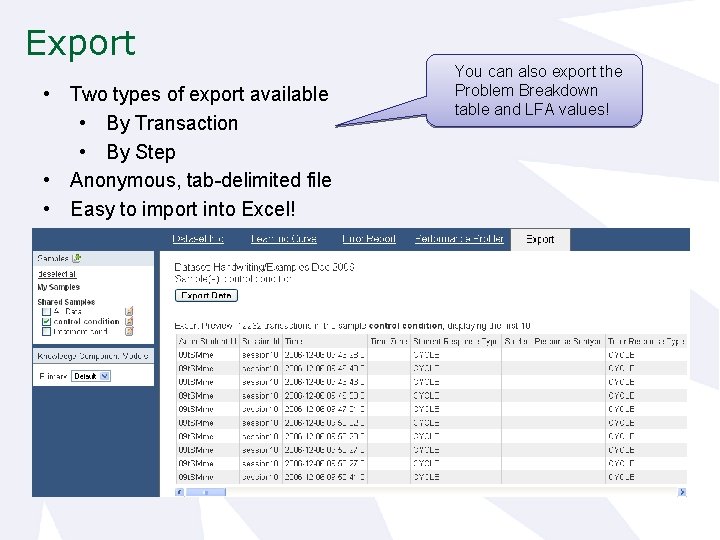
Export • Two types of export available • By Transaction • By Step • Anonymous, tab-delimited file • Easy to import into Excel! You can also export the Problem Breakdown table and LFA values!

Help/Documentation Glossary of common terms, tied in with PSLC Theory wiki • • • Extensive documentation with examples Contextual by tool/report http: //learnlab. web. cmu. edu/datashop/help

New Features n Manage Knowledge Component models q n Addition of Latency Curves to Learning Curve Reporting q q n n Create, Modify & Delete KC models within Data. Shop Time to Correct Assistance Time Problem Rollup & Export Enhanced Contextual Help

Overview n Data. Shop Overview q q n Quantitative models of learning curves q q n n Logging model Data. Shop Features Power law, logistic regression Contrasting KC models Exploratory Data Analysis Exercise (start) Knowledge Component Model Editing

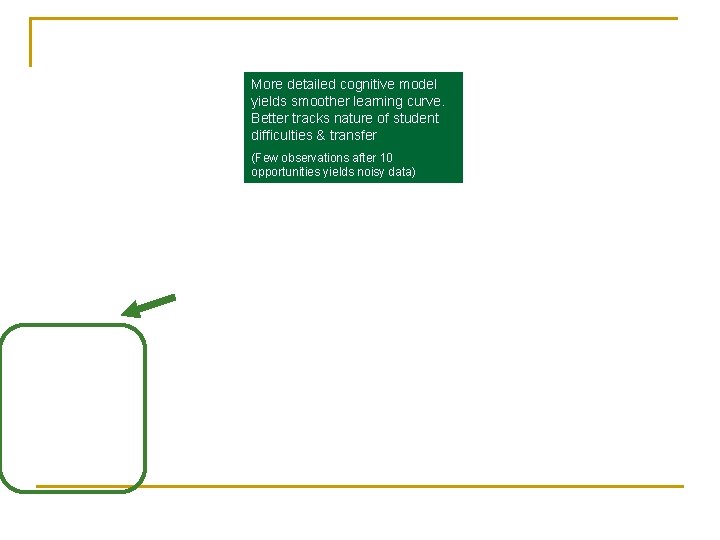
Recall learning curve story Without decomposition, using just a single “Geometry” KC, no smooth learning curve. But with decomposition, 12 KCs for area concepts, a smooth learning curve. Upshot: A decomposed KC model fits learning & transfer data better than a “faculty theory” of mind

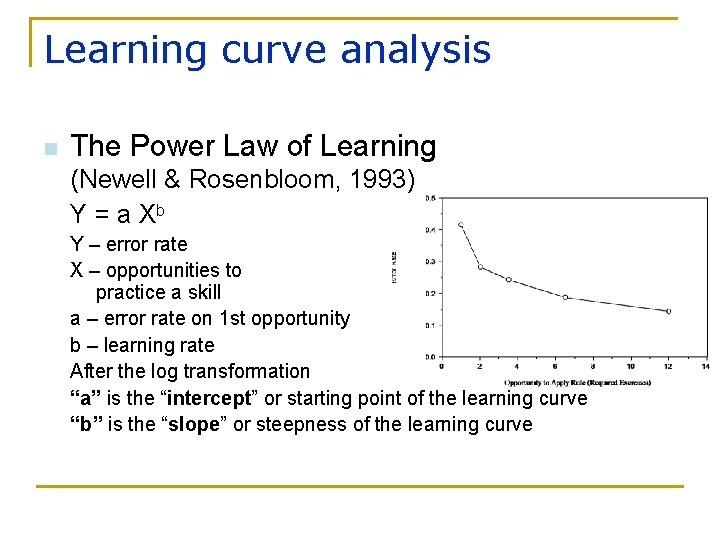
Learning curve analysis n The Power Law of Learning (Newell & Rosenbloom, 1993) Y = a Xb Y – error rate X – opportunities to practice a skill a – error rate on 1 st opportunity b – learning rate After the log transformation “a” is the “intercept” or starting point of the learning curve “b” is the “slope” or steepness of the learning curve

More sophisticated learning curve model n Generalized Power Law to fit learning curves q n Logistic regression (Draney, Wilson, Pirolli, 1995) Assumptions q q Different students may initially know more or less => use an intercept parameter for each student Students learn at the same rate => no slope parameters for each student q Some productions may be more known than others => use an intercept parameter for each production q Some productions are easier to learn than others => use a slope parameter for each production n These assumptions are reflected in detailed math model …

More sophisticated learning curve model p Probability of getting a step correct (p) is proportional to: - - if student i performed this step = Xi, add overall “smarts” of that student = i if skill j is needed for this step = Yj, add easiness of that skill = j add product of number of opportunities to learn = Tj & amount gained for each opportunity = j Use logistic regression because response is discrete (correct or not) Probability (p) is transformed by “log odds” “stretched out” with “s curve” to not bump up against 0 or 1 (Related to “Item Response Theory”, behind standardized tests …)

Different representation, same model n n Predicts whether student is correct depending on knowledge & practice Additive Factor Model (Draney, et al. 1995, Cen, Koedinger, Junker, 2006)

The Q Matrix n How to represent relationship between knowledge components and student tasks? q n Tasks also called items, questions, problems, or steps (in problems) Q-Matrix (Tatsuoka. 1983) Item | KC q q Add Sub Mul Div 2*8 0 0 1 0 2*8 - 3 0 1 1 0 2* 8 is a single-KC item 2*8 – 3 is a conjunctive-KC item, involves two KCs 29

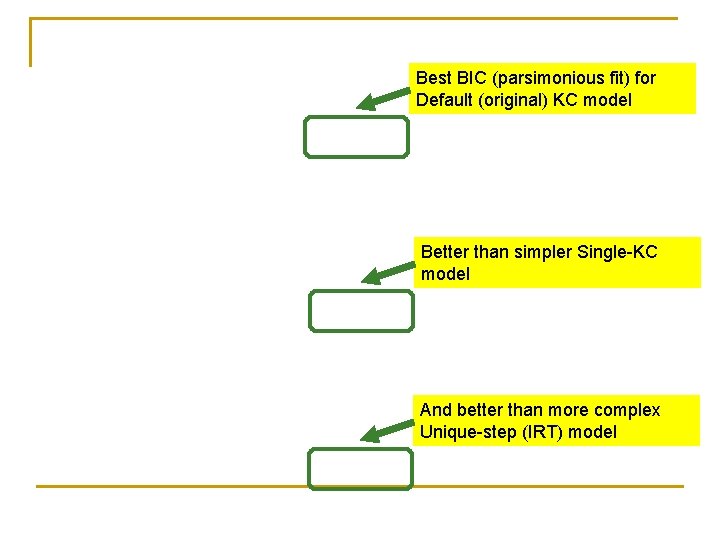
Model Evaluation • How to compare cognitive models? • A good model minimizes prediction risk by balancing fit with data & complexity (Wasserman 2005) • Compare BIC for the cognitive models • BIC is “Bayesian Information Criteria” • BIC = -2*log-likelihood + num. Par * log(num. Ob) • Better (lower) BIC == better predict data that haven’t seen • Mimics cross validation, but is faster to compute 30

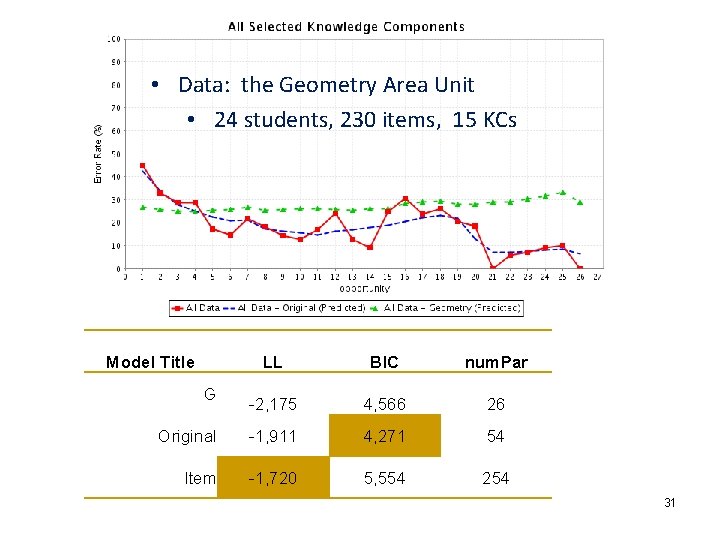
• Data: the Geometry Area Unit • 24 students, 230 items, 15 KCs Model Title LL BIC num. Par -2, 175 4, 566 26 Original -1, 911 4, 271 54 Item -1, 720 5, 554 254 G 31

Learning curve constrast in Physics dataset …

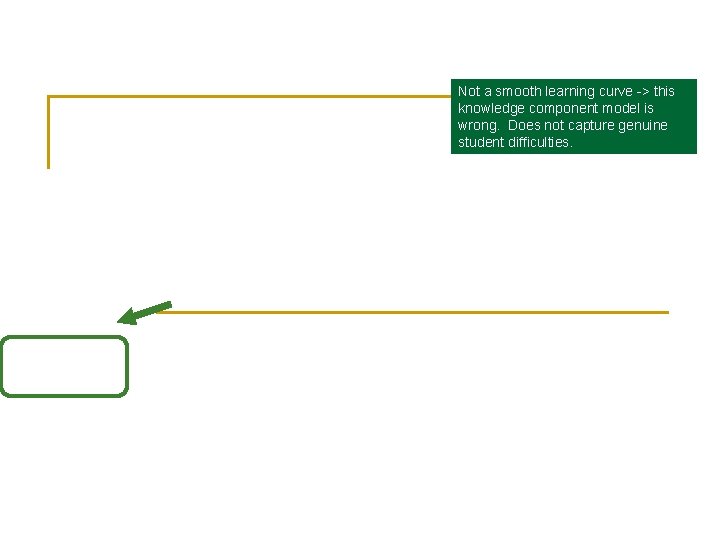
Not a smooth learning curve -> this knowledge component model is wrong. Does not capture genuine student difficulties.

More detailed cognitive model yields smoother learning curve. Better tracks nature of student difficulties & transfer (Few observations after 10 opportunities yields noisy data)

Best BIC (parsimonious fit) for Default (original) KC model Better than simpler Single-KC model And better than more complex Unique-step (IRT) model

Overview n Data. Shop Overview q q n Quantitative models of learning curves q q n n Logging model Data. Shop Features Power law, logistic regression Contrasting KC models Exploratory Data Analysis Exercise (start) Knowledge Component Model Editing

Exploratory Data Analysis Exercise n n Goals: 1) Get familiar with data 2) Learn/practice Excel skills Tasks: 1) create a “step table” 2) graph learning curves

TWO_CIRCLES_IN_SQUARE problem: Initial screen

TWO_CIRCLES_IN_SQUARE problem: An error a few steps later

TWO_CIRCLES_IN_SQUARE problem: Student follows hint & completes prob

Exported File Loaded into Excel

See handout of exercise … Do some of in next session

Overview n Data. Shop Overview q q n Quantitative models of learning curves q q n n Logging model Data. Shop Features Power law, logistic regression Contrasting KC models Exploratory Data Analysis Exercise (start) Knowledge Component Model Editing

Data. Shop Demo n Examples of exercise n KC model editing

END