EdgeColoring of Graphs On the left we see

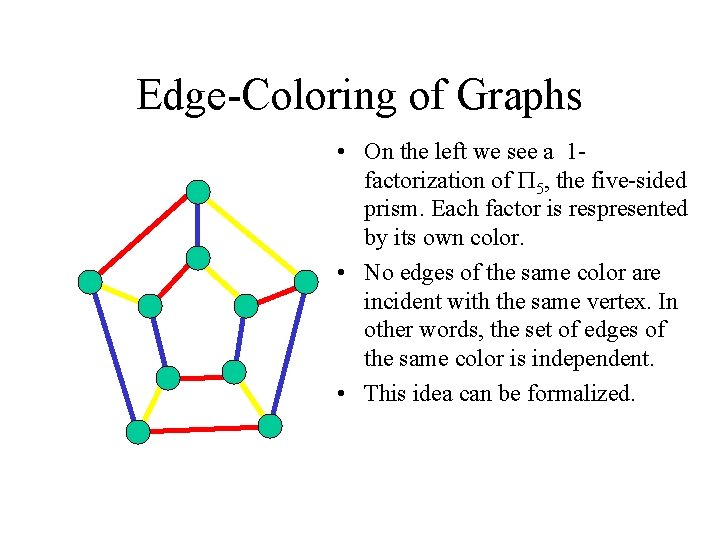
Edge-Coloring of Graphs • On the left we see a 1 factorization of P 5, the five-sided prism. Each factor is respresented by its own color. • No edges of the same color are incident with the same vertex. In other words, the set of edges of the same color is independent. • This idea can be formalized.

Edge-Coloring of Graphs • A mapping c: E(G) C from the edges set E(G) to some finite set C is called an (admissible) edge coloring, if eny two edges e and f with a common endvertex c(e) c(f). • The least number of colors neede to properly color the edges of G is called c chromatic index and is denote by c’(G).

Vizing’s Theorem • Theorem: The chromatic index of a simle graph G satisfies the following inequalities: • D(G) c’(G) D(G)+1 • Proof. Lower bound immediate, the upper bound more difficult to prove. • Using Vizing’s theorem we may now classify simple graphs into two types. A graph of type I has c’(G) = D(G), while the graph of type II has c’(G) = D(G)+1.

Consequences • Corollary: Regular graph is of type I, if and only if it has a 1 -factorization. • Example: Petersen graph is of type II. • Even if we replace a vertex by a triangle in Petersen graph, the graph remains of type II.

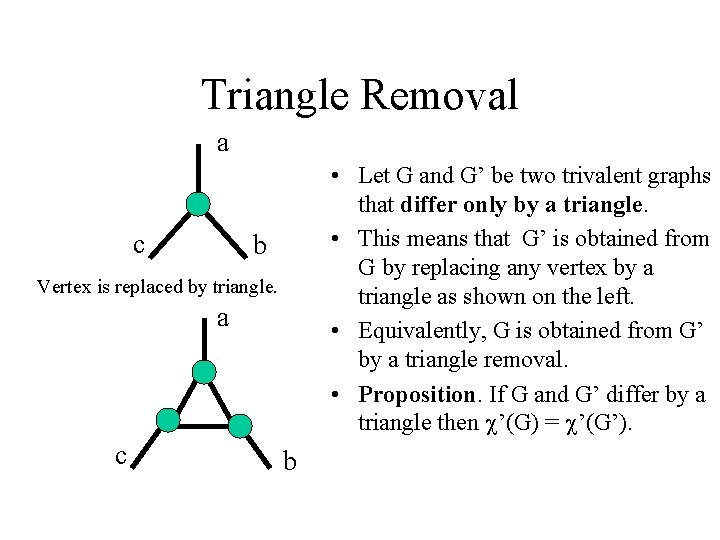
Triangle Removal a c • Let G and G’ be two trivalent graphs that differ only by a triangle. • This means that G’ is obtained from G by replacing any vertex by a triangle as shown on the left. • Equivalently, G is obtained from G’ by a triangle removal. • Proposition. If G and G’ differ by a triangle then c’(G) = c’(G’). b Vertex is replaced by triangle. a c b

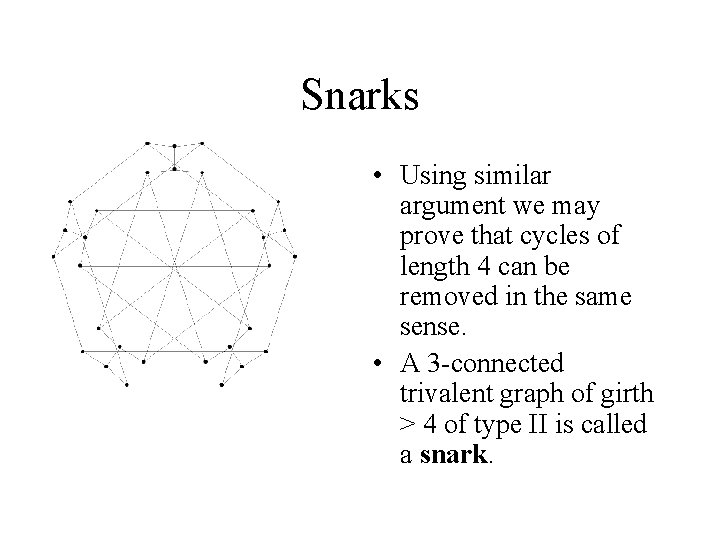
Snarks • Using similar argument we may prove that cycles of length 4 can be removed in the same sense. • A 3 -connected trivalent graph of girth > 4 of type II is called a snark.

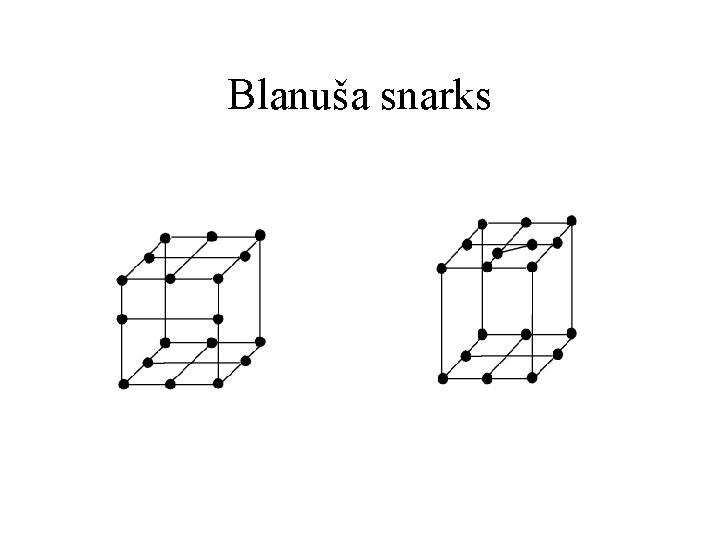
Families of Snarks • There are several infinite families of snarks known. • Blanuša found the first snark after Petersen.

Blanuša snarks

König Theorem • Theorem (König): For a bipartite graph G we have c’(G) = D(G).

Exercises • N 1. Show that there are no bipartite snarks. • N 2. Repeatedly remove all quadrilaterals and triangles in K 3, 3. What simple graph is obtained in the end? • N 3. Dot product!

Vertex Coloring of Graphs. • Mapping c: V(G) C from the vertex set to a finite set of colors is called vertex coloring, if for any pair of adjacent vertices u ~ v we have c(u) c(v). • The least number of colors of some proper vertex coloring of G is called the chromatic number and is denoted by c(G).

Brooks Theorem • For any connected graph G the following holds: • c(G) = D(G)+ 1, if G is isomorphic to a complete graph or an odd cycle. • c(G) · D(G), otherwise.

Four Color Theorem • A theorem posed in the 19 th century and proved in the 20 th century. • Theorem: c(G) · 4, for any planar graph G.

Graph Mappings (Homomorphisms) • Let : V(G) ! V(H) be a mapping between the vertices of two graphs. is called a graph mapping or graph homomorphism if for any pair of vertices u, v 2 V(G) the fact u ~ v implies (u) ~ (v).

More general maps – Weak homomorphism • Sometimes we allow graph maps that do not preserve dimension. : V(G) ! V(H) and u ~ v implies (u) ~ (v) or (u) = (v). • Such phi is called a weak homomorphism.

Retracts • Let : G ! G be a graph homorphism. Then is called a retraction if 2 = . (idempotent). (G) = H has the property that |H = id. H is called a retract. • In a similar way one can define a weak retraction and weak retract.

Colorings revisited. • A vertex coloring c with h colors can be defined as a graph homomorphism c: G ! Kh

Exercises • N 1. Prove that retracts and weak retracts are isometric subgraphs. • N 2(*). A graph G is called a median graph if for any triple of vertices u, v, w we have |I(u, v) Å I(v, w) Å I(w, u)| = 1. Prove that G is a median graph if and only if it is retract of some hypercube.