Edge Detection Using ICA Supervisor Dr Longin Jan

Edge Detection Using ICA Supervisor: Dr. Longin Jan Latecki Presenter: Guoqiang Shan Class: CIS 601 Computer Graphics and Image Processing Date: December 6, 2004 2020/9/26 1

Basic Idea n Consider the difference of the corresponding pixels between images n A pixel is independent from each other n Pros: Limit the scope of any condition n Cons: No relation among neighbor pixels n Similar as letter detection & motion detection n Representing locality is important n Locality: neighbor pixels tend same value 2020/9/26 2

Quick Tip of ICA n X(k) = A*S(k) S: m*n, m independent signals length n n X: m*n, m mixed signals length n n A: m*m, each column of A is a basic vector n S(k) = W*X(k) n W: m*m, separating independent signals from mixed signals n 2020/9/26 3

S (j, : ) = average image? n a: Frame 50 n 2020/9/26 c: 1 Component of ICA n b: Frame 55 n d: Average Image 4

Why? n 2 images: W = [-0. 0549 0. 0553; 0. 0083 0. 0102]; n => c = 0. 45 a+0. 55 b n Diff (c, d) < 0. 19% n 4 images: n Diff (c, d) < 0. 25% n 2020/9/26 5

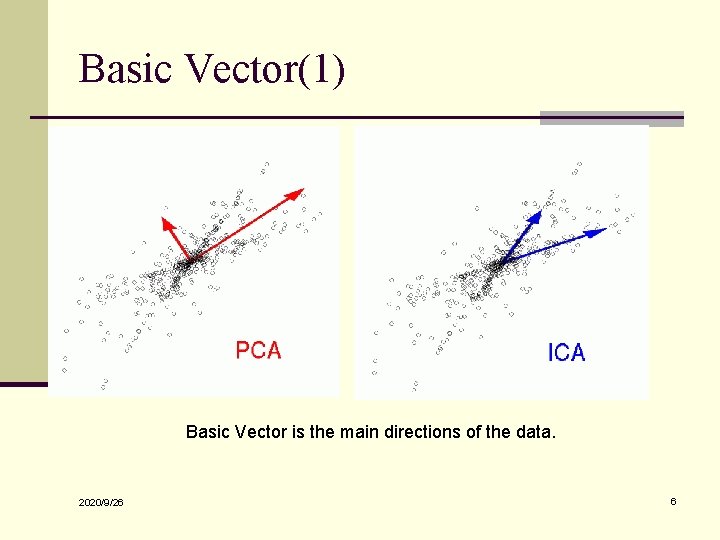
Basic Vector(1) Basic Vector is the main directions of the data. 2020/9/26 6

Basic Vector(2) n A= n [9. 988 54. 280 - 8. 166 53. 940]; Conclusion: One of basic vector is approximately the diagonal. 2020/9/26 7

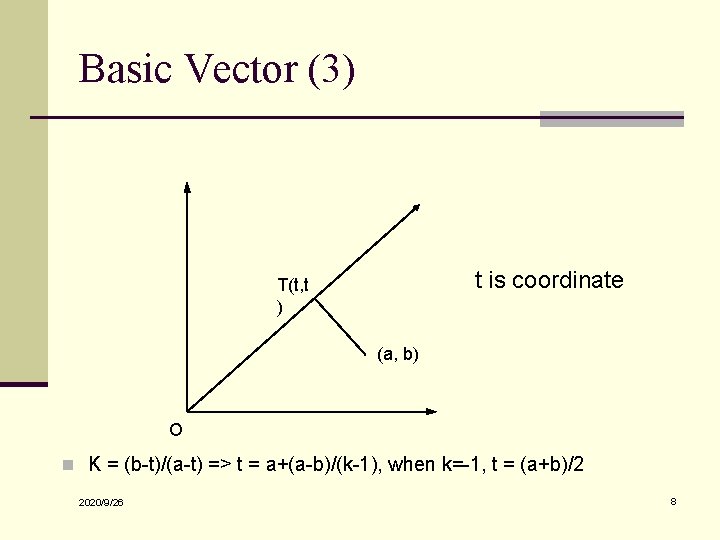
Basic Vector (3) t is coordinate T(t, t ) (a, b) O n K = (b-t)/(a-t) => t = a+(a-b)/(k-1), when k=-1, t = (a+b)/2 2020/9/26 8

Sense on ICA n One basic vector of ICA is the diagonal, or say, one component shows the common feature among images, if: n the mixed images are similar enough n # of images is not large n Other components of ICA show the difference among images 2020/9/26 9

Average Image as substitute? n No! n For the points changing a lot among images, average image can not give a good result. The points are just the points we need care more about. n My proof is to obtain sense, not for simplifying the calculation. n ICA calculation is still necessary. 2020/9/26 10

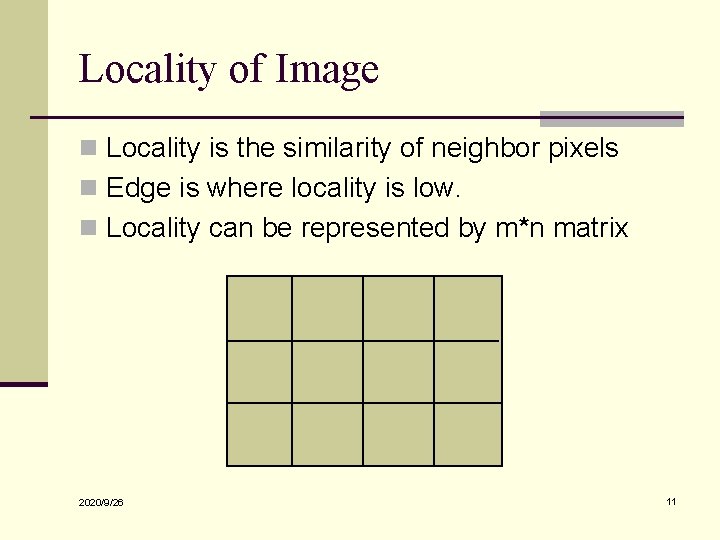
Locality of Image n Locality is the similarity of neighbor pixels n Edge is where locality is low. n Locality can be represented by m*n matrix 2020/9/26 11

Locality vs. one component of ICA n Locality is similarity n One component shows common features among corresponding pixels n They can be connected! 2020/9/26 12

Reshape the matrix 2020/9/26 13

One image => Several Images n To connect locality with ICA component, consider the reshaped vector as column of X n If the size of the image is X*Y, we have (X -m+1)*(Y-n+1) vectors. They consist of X. n X is the overlap of the original image. Each image starts at (1. . m, 1. . n). Different image starts differently. 2020/9/26 14

Remove component Sj n X is ready, run ICA. n Sj = locality, thus remove Sj and the corresponding basic vector Aj. n Reconstruct one of the overlapped images by other signals and other basic vectors. n The image will show only low locality, edges. 2020/9/26 15

This method vs. 3*3 Operators (1) n 3*3 operators have pre-defined coefficients. n This method has self-adaptive coefficients. n What is the coefficient matrix? Let A’ = A after removing Aj, A’*W is matrix. n They’re the optimal coefficients for a particular image. n 2020/9/26 16

This method vs. 3*3 Operators (2) n 3*3 operators have pre-defined number of coefficients. n This method has a flexible number of coefficients. n The flexibility provides a better choice if the edges are mainly vertical or horizontal. 2020/9/26 17

Experiments (1) n Original Images 2020/9/26 18

Experiments (2) n Edge detection by 3*3 operator and ICA 2020/9/26 19

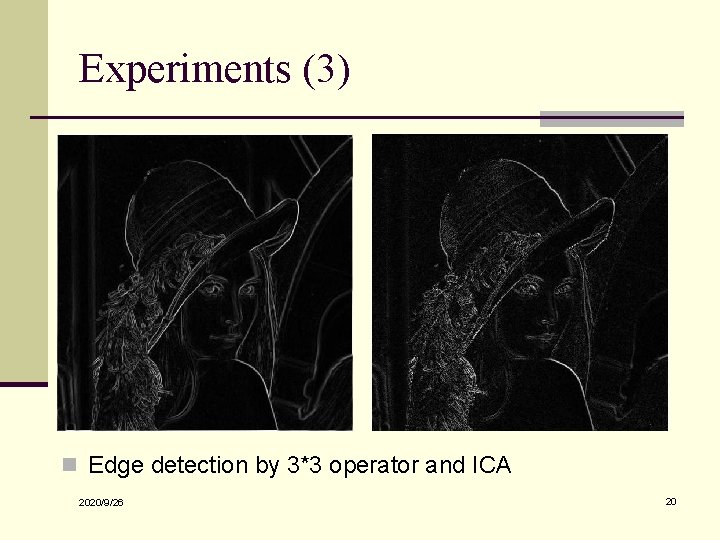
Experiments (3) n Edge detection by 3*3 operator and ICA 2020/9/26 20

Experiments (4) Original Image 2020/9/26 By most of 3*3 operator By this method 21

Experiments (5) n 2020/9/26 n Original Image 3*3 Operator I plane after RGB 2 YIQ This method 22

Conclusion n ICA provides a solution for edge detection. n The solution provides the more accurate coefficients, compared to 3*3 operators. n It configures the locality window size flexibly. n It can recognize some edges, unable to be done by 3*3 operators. 2020/9/26 23

Future work n Pre-processing on the image for edge detection n Post- processing on result by this method n Find the best locality window not by try n Find what kind of images it is proper to use and what kind is improper. n How to use ICA more efficiently? 2020/9/26 24

Reference n Roberts and Everson, Independent Component Analysis – Principles and Practice, Cambridge University Press, 2001 n Paper and software on http: //www. cis. hut. fi/projects/ica/ n Comparison of edge detection methods on http: //robotics. eecs. berkeley. edu/~mayi/imgproc/ n Video Analysis using Principal Component Analysis http: //knight. cis. temple. edu/~video/VA/ 2020/9/26 25