Edge Detection Edges local changes in the image

Edge Detection • Edges: local changes in the image intensity • Edges typically occur on the boundary between two regions • Important features for image analysis • The changes due to noise are not edges – real images are very noisy – its very difficult to find edges in noisy images • The changes due to shading are not edges E. G. M. Petrakis Edge Detection 1

line of profile I. II. Original noisy image Edge profile • The edges are not perfectly sharp E. G. M. Petrakis Edge Detection 2

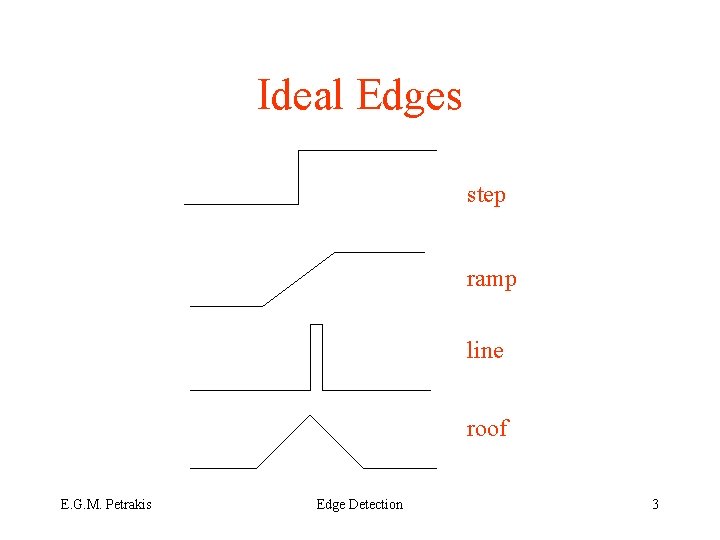
Ideal Edges step ramp line roof E. G. M. Petrakis Edge Detection 3

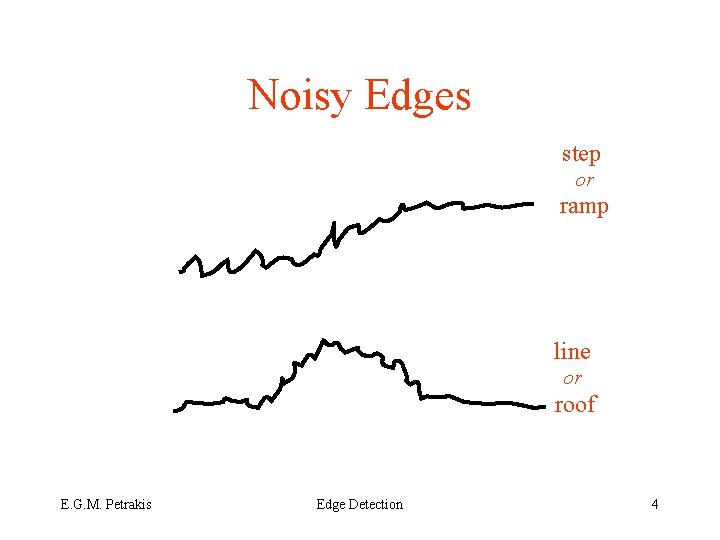
Noisy Edges step or ramp line or roof E. G. M. Petrakis Edge Detection 4

Edge Detection • An edge point is a point at the location of a local intensity change • An edge detector is an algorithm that computes the edges in an image • A contour is a list of edges or the curve that matches the list of edges • Edge following is the process of searching the image to determine contours E. G. M. Petrakis Edge Detection 5

Edge Results • The produced set of edges contain – correct edges corresponding to real - useful information e. g. , object boundaries – false edges do not correspond to real edges e. g. , noise • There also missing edges – edge linking may try to recover missing edges – edge following will form contours from existing and recovered edges E. G. M. Petrakis Edge Detection 6

First Derivative Operator • Gradient: vector denoting the max rate of change of intensity f(x, y): – direction – magnitude E. G. M. Petrakis Edge Detection 7

Gradient • For any vertical directions (x, y), (x’, y’) and image f(x, y): E. G. M. Petrakis Edge Detection 8

Digital Approximation of Gradient • Compute • Equivalently convolve with E. G. M. Petrakis Edge Detection 9

Gradient Convolution Masks • • computes edge point at (i, j+1/2) computes edge point at (i+1/2, j) • 2 x 2 masks: edge point at (i+1/2, j+1/2) • edge points at center pixel (i, j) use 3 x 3 masks E. G. M. Petrakis Edge Detection 10

Roberts operator • Computes the edge at the interpolated point (i+1/2, j+1/2) – magnitude: |Gx| + |Gy| E. G. M. Petrakis Edge Detection 11

Sobel Operator • One the most commonly used edge operators – computes the edge at (i, j) – Smoothing at the same time – places emphasis on pixels closest to (i, j) E. G. M. Petrakis Edge Detection 12

Prewit Operator • Similar to Sobel but does not place any emphasis on pixels E. G. M. Petrakis Edge Detection 13

Edge Filtering • Assuming that noise intensity is lower than the intensity of edges – Specify threshold T – Edge: points with intensity > T – Non Edge: points with intensity < T • Some edge points are lost – Some noisy points may have intensity > T – Some edge points may have intensity < T E. G. M. Petrakis Edge Detection 14

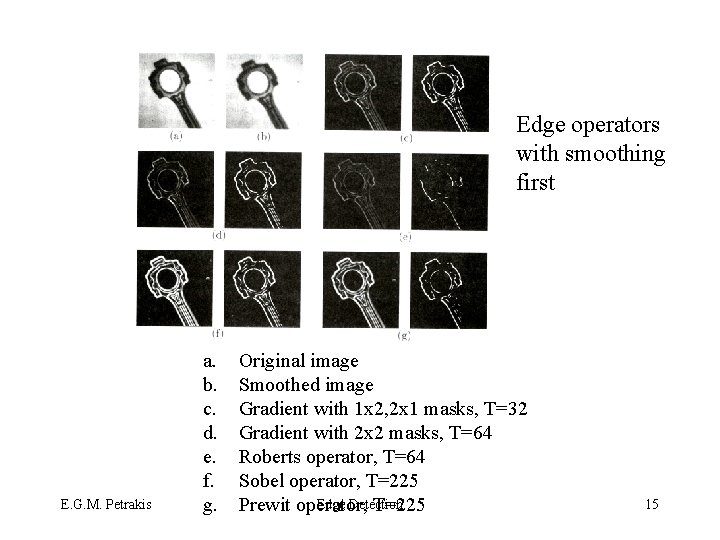
Edge operators with smoothing first E. G. M. Petrakis a. b. c. d. e. f. g. Original image Smoothed image Gradient with 1 x 2, 2 x 1 masks, T=32 Gradient with 2 x 2 masks, T=64 Roberts operator, T=64 Sobel operator, T=225 Edge Detection Prewit operator, T=225 15

Edge operators without smoothing a. b. c. d. e. f. E. G. M. Petrakis Original image Simple Gradient with 1 x 2, 2 x 1 masks, T=64 Gradient with 2 x 2 masks, T=64 Roberts operator, T=64 Sobel operator, T=225 Prewitt operator, T=225 Edge Detection 16

Edge operators with smoothing on noisy image E. G. M. Petrakis a. b. c. d. e. f. g. Noisy image Filtered image Simple Gradient with 1 x 2, 2 x 1 masks, T=32 Gradient with 2 x 2 masks, T=64 Roberts operator, T=64 Sobel operator, t=225 Prewitt operator, T=225 Edge Detection 17

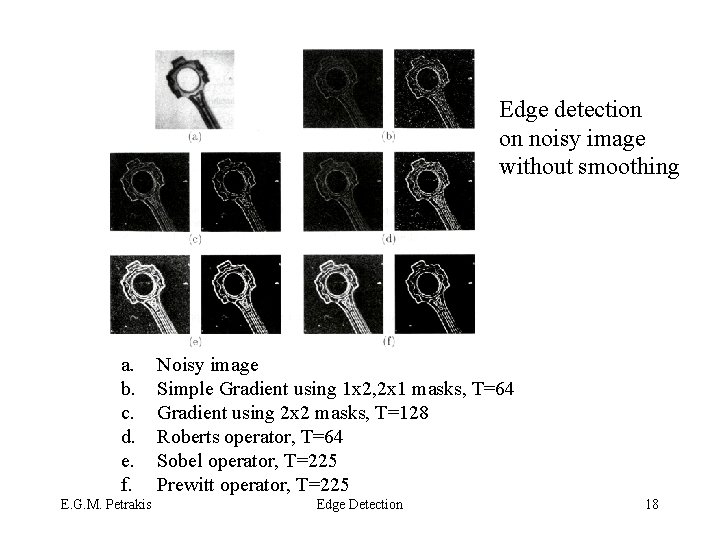
Edge detection on noisy image without smoothing a. b. c. d. e. f. E. G. M. Petrakis Noisy image Simple Gradient using 1 x 2, 2 x 1 masks, T=64 Gradient using 2 x 2 masks, T=128 Roberts operator, T=64 Sobel operator, T=225 Prewitt operator, T=225 Edge Detection 18

Edge Detection with Edge Patterns • Comparison (filtering) with 4 or 8 edge masks – each one represents an edge orientation – combine their results – the edge pattern with the max magnitude represents the magnitude and the orientation of the edge – thresholding is still necessary! • Optimization: apply 4 of the 8, the other 4 are symmetric • give opposite orientations and negative values of magnitude • take the absolute value of negative edge strengths E. G. M. Petrakis Edge Detection 19

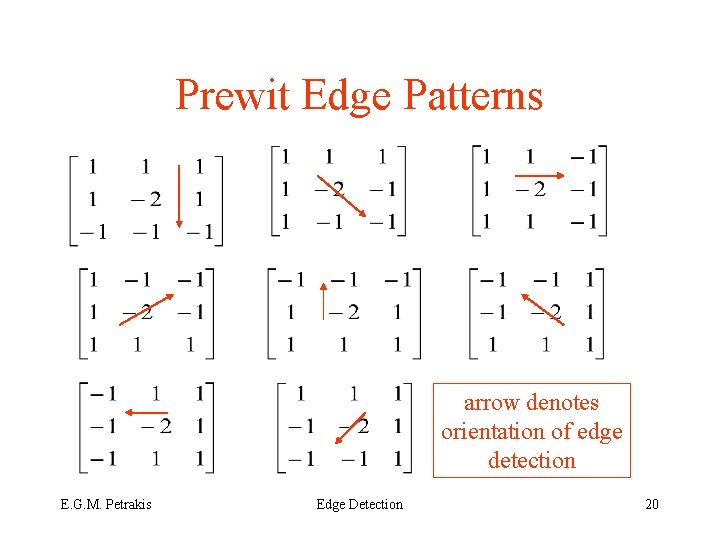
Prewit Edge Patterns arrow denotes orientation of edge detection E. G. M. Petrakis Edge Detection 20

Kirsch edge patterns arrow denotes orientation of edge detection E. G. M. Petrakis Edge Detection 21

Steps in Edge Detection 1. Filtering removes noise and improves the performance of edge detection – – 2. 3. Edge enhancement apply a Gradient operator Detection keeps only edge points and eliminates false edge points – – 4. there is a trade off between edge strength and noise reduction filtering smoothes the edge too!! keep points with strong edge content above a threshold T Localization computes location and orientation of edge E. G. M. Petrakis Edge Detection 22

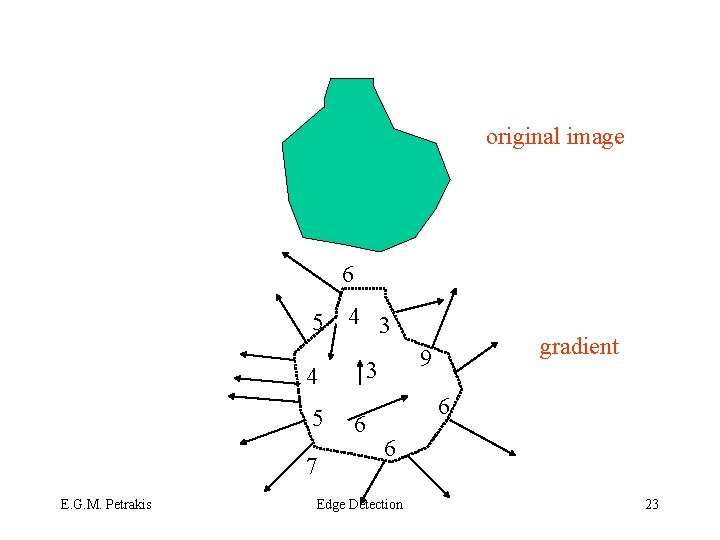
original image 6 5 4 3 3 4 5 7 E. G. M. Petrakis 6 gradient 9 6 6 Edge Detection 23

Detection and Localization 6 thershold T= 4 keep edges points with strength > 4 noise is retained 5 9 5 7 6 6 thershold T= 5 keep edges points with strength > 5 removes noise but significant parts of the contour are lost E. G. M. Petrakis Edge Detection 9 6 7 6 6 24

Smoothing & Thresholding • Smoothing: – high degree of smoothing (large mask, repeated smoothing) removes noise but blurs the edges – low degree of smoothing retains noise • Threshold selection: – large thresholds remove noise along with edge points – low thresholds retain noise E. G. M. Petrakis Edge Detection 25

Second Derivative Operators • Edge points: peaks of the first derivative – use of thresholds – detects too many edge points • Equivalently, zero’s of the second derivative • Combine first and second derivatives – locate peak in the first derivative and zero crossing in the second derivative E. G. M. Petrakis Edge Detection 26

Combination of Derivatives • Edge detection – smoothing by Gaussian – presence of zero crossing in second derivative – large peak in the first derivative E. G. M. Petrakis Edge Detection 27

all points in [a, b] are edge points edge point E. G. M. Petrakis Edge Detection 28

Laplacian Operator • Two dimensional equivalent of the second derivative • Digital approximation E. G. M. Petrakis Edge Detection 29

Proof E. G. M. Petrakis Edge Detection 30

Proof (2) • Second derivative on X is centered around [i, j+1], – replace j with j-1 to center edge around [i, j] • Similarly for Y E. G. M. Petrakis Edge Detection 31

Laplacian Mask • The following mask approximates the Laplacian (both x, y) E. G. M. Petrakis Edge Detection 32

Response of Laplacian • Zero’s signal the presence of an edge – trivial zeros (uniform regions) are ignored – strong response to edges, lines, points, noise! E. G. M. Petrakis Edge Detection 33

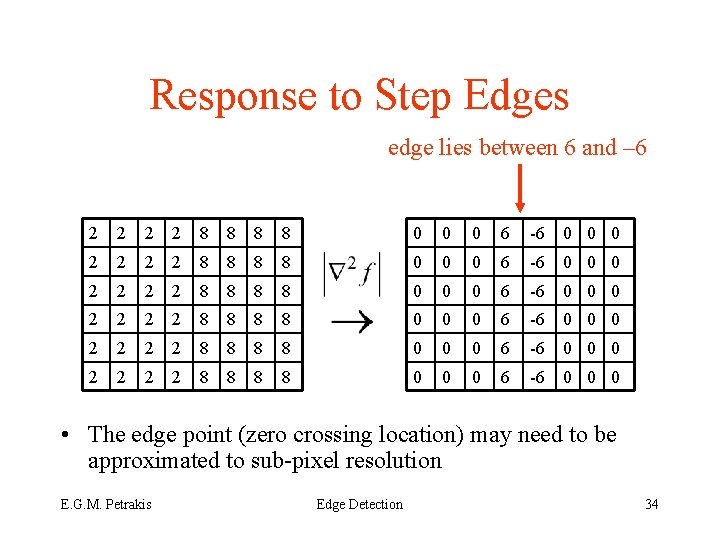
Response to Step Edges edge lies between 6 and – 6 2 2 2 2 8 8 8 8 0 0 0 6 -6 0 0 0 2 2 2 2 8 8 8 8 0 0 0 6 -6 0 0 0 • The edge point (zero crossing location) may need to be approximated to sub-pixel resolution E. G. M. Petrakis Edge Detection 34

Response to Ramp Edges 2 2 2 2 5 8 8 8 8 0 0 0 3 0 -3 0 0 0 2 2 2 2 5 8 8 8 8 0 0 0 3 0 -3 0 0 0 edge E. G. M. Petrakis Edge Detection 35

Laplacian of Gaussian • The second derivative responds strongly to noise • It is desired to filter the noise before edge detection • The Laplacian of a Gaussian (Lo. G) combines Gaussian filtering with Laplacian for edge detection E. G. M. Petrakis Edge Detection 36

One-Step Lo. G • Notice that • In practice Lo. G is applied in one step by filtering with • Known also as Mexican hat operator E. G. M. Petrakis Edge Detection 37

Discrete Approximation of Lo. G E. G. M. Petrakis Edge Detection 38

Lo. G Smoothing • σ controls the degree of smoothing – – large σ results in better noise filtering but also blurs and displaces edges small σ results in too many noise points and false edges edge points are better localized using small σ • The best size of the filter is unknown • Scale space filtering: combine results from multiple filters with varying – resembles filtering on the retina E. G. M. Petrakis Edge Detection 39

Lo. G filtering with varying σ E. G. M. Petrakis Edge Detection 40

Do. G Approximation of Lo. G • The best engineering approximation of Lo. G is obtained by taking the Difference of two Gaussians (Do. G) with – amplitude ratio 1: 1. 16 • The same mechanism operates in the retina – many filters with varying σ E. G. M. Petrakis Edge Detection 41

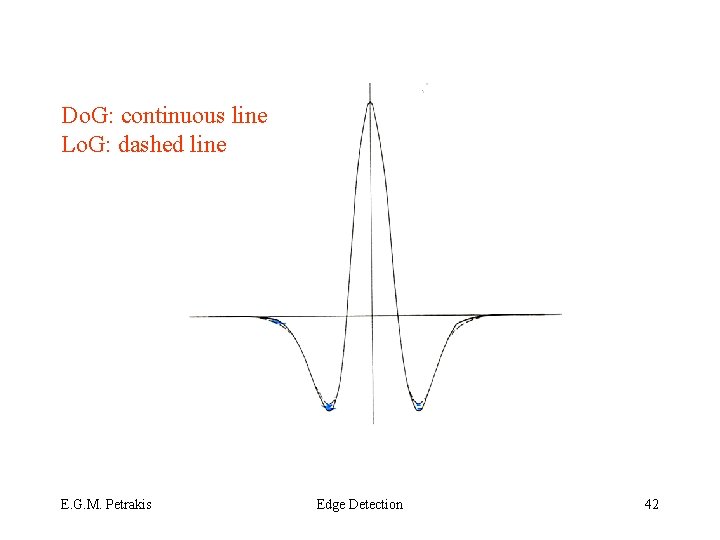
Do. G: continuous line Lo. G: dashed line E. G. M. Petrakis Edge Detection 42

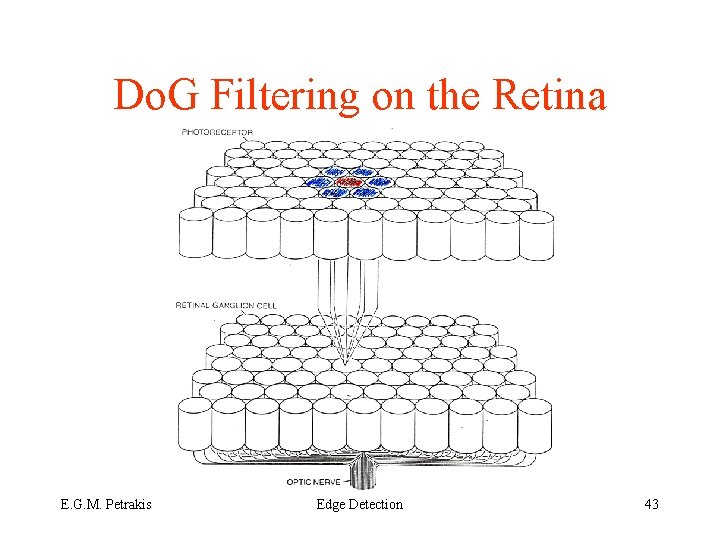
Do. G Filtering on the Retina E. G. M. Petrakis Edge Detection 43

“Center-Surround” Filtering • Filtering by cells in retina resemble the effects of Do. G – the photoreceptors are connected to retinal gaglion cells which send visual data to the brain – “Red” photoreceptors excite “ON center” gaglion cells (generate neural signals) – “Blue” photoreceptors in its surrounding inhibit the gaglion cell “OFF surround” E. G. M. Petrakis Edge Detection 44