Economics Chapter 10 Price elasticity of Demand Supply

Economics Chapter 10 Price elasticity of Demand Supply

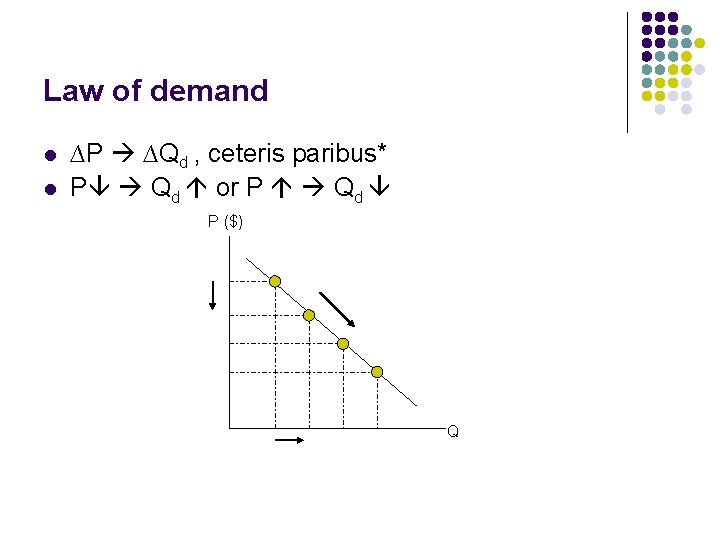
Law of demand l l ∆P ∆Qd , ceteris paribus* P Qd or P Qd P ($) Q

Given Qd (unit /day) Price Toy Car Doll $100 20 $90 110 40 1. When price , Qd ? Qd of toy car Qd of doll 2. Which one shows greater effect when P by 10%? Qd of toy car: 10 units / 10% Qd of doll: 20 units / 100% ∴ Doll reflects greater respond to ∆P

Price elasticity of demand l l l Measures the responsiveness of quantity demanded to a change in price Percentage change in quantity demanded over one percent change in price % ∆ Qd Ed = -----%∆ P

Price elasticity of demand l l Example (p. 75) When P

Price elasticity of demand l l Example (p. 76) When P

Price elasticity of demand l l Example (p. 76) Midpoint formula

Price elasticity of demand Qd (unit /day, P=$100) Qd (unit /day, P=$90) l Toy Car Doll 100 20 110 40 Calculate Ed of toy car and doll when l l l Prices drop Prices rise By using midpoint formula

Price elasticity of demand l Given a straight line demand curve : Slope of demand curve = 6 -0 / 0 -6 = -1 Slope = 1, with negative relationship between P and Qd l Price elasticity: If ∆P = $6 $0, ∆ Qd = 0 unit 6 units Ed = %∆ Qd / %∆P = (∆ Qd / Average Qd ) / (∆P / Average P) = [(6 -0) / ((6+0)/2)] / [(0 -6) / ((6+0)/2))] = -1 Is Ed = Slope of straight line demand curve? l

Price elasticity of demand l If ∆P = $5 $4, ∆ Qd = 1 unit 2 units Ed = %∆ Qd / %∆P = (∆ Qd / Average Qd ) / (∆P / Average P) = [(2 -1) / ((2+1)/2)] / [(5 -4) / ((4+5)/2)] = (1/1. 5) / (1/4. 5) = 3 l Slope of demand curve = 1 Ed ≠Slope of demand curve? l

Price elasticity of demand l If ∆P = $4 $3, ∆ Qd = 2 unit 3 units Ed = %∆ Qd / %∆P = (∆ Qd / Average Qd ) / (∆P / Average P) = [(3 -2) / ((3+2)/2)] / [(4 -3) / ((4+3)/2)] = (1/2. 5) / (1/3. 5) = 1. 4 l Slope of demand curve = 1 Ed ≠Slope of demand curve? l

Price elasticity of demand l If ∆P = $3 $2, ∆ Qd = 3 unit 4 units Ed = %∆ Qd / %∆P = (∆ Qd / Average Qd ) / (∆P / Average P) = [(4 -3) / ((4+3)/2)] / [(3 -2) / ((3+2)/2)] = (1/3. 5) / (1/2. 5) = 0. 714 l Slope of demand curve = 1 Ed ≠Slope of demand curve? l

Price elasticity of demand l If ∆P = $2 $1, ∆ Qd = 4 unit 5 units Ed = %∆ Qd / %∆P = (∆ Qd / Average Qd ) / (∆P / Average P) = [(5 -4) / ((5+4)/2)] / [(2 -1) / ((2+1)/2)] = (1/4. 5) / (1/1. 5) = 0. 33 l Slope of demand curve = 1 Ed ≠Slope of demand curve? l

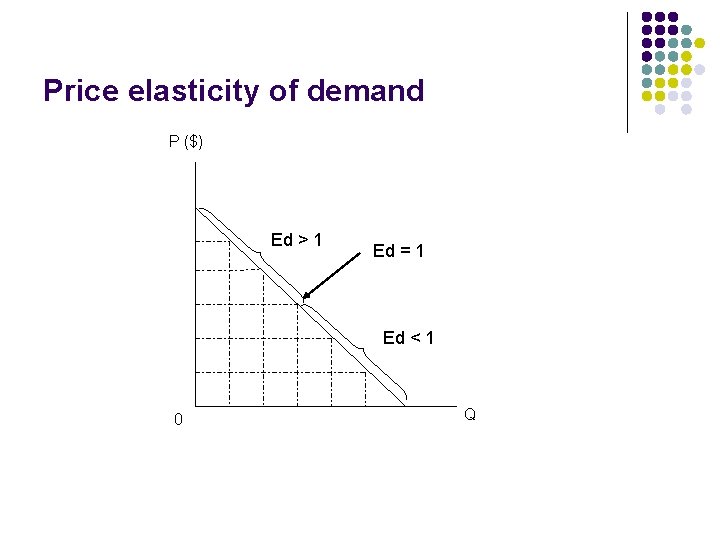
Price elasticity of demand P ($) Ed > 1 Ed = 1 Ed < 1 0 Q

5 Types of elasticity of demand l Elastic demand l l l Elasticity is greater than 1 (Ed > 1) Percentage change in quantity demanded is greater than percentage change in price (%∆ Qd > %∆P) Example l Toys P ($) D 0 Q

5 Types of elasticity of demand l Inelastic demand l l l Elasticity is smaller than 1 (Ed < 1) Percentage change in quantity demanded is smaller than percentage change in price (%∆ Qd < %∆P) Example l Transportation P ($) 0 D Q

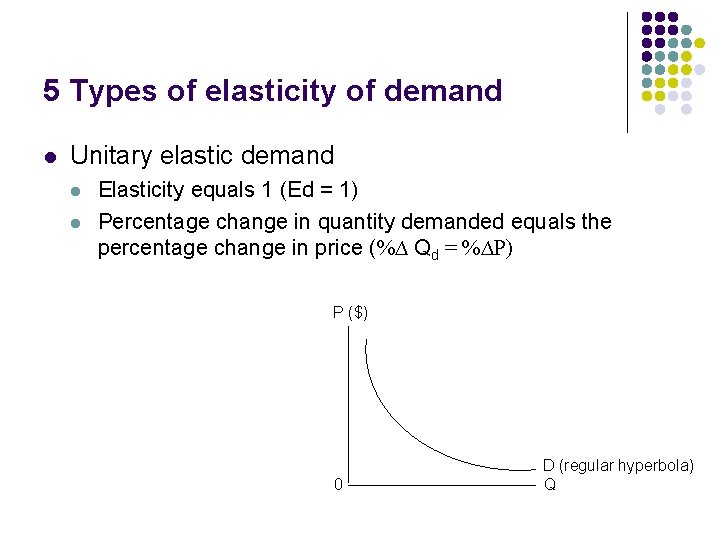
5 Types of elasticity of demand l Unitary elastic demand l l Elasticity equals 1 (Ed = 1) Percentage change in quantity demanded equals the percentage change in price (%∆ Qd = %∆P) P ($) 0 D (regular hyperbola) Q

5 Types of elasticity of demand l Perfectly elastic demand l l l Elasticity equals infinity (Ed = ∞) A slightly rise in price will cause quantity demanded fall to 0. i. e. %∆P Example: Lucky draw ticket P ($) D (horizontal) 0 Q

5 Types of elasticity of demand l Perfectly inelastic demand l l l Elasticity equals 0 (Ed = 0) Price change has no effect on the quantity demanded. (i. e. %∆Qd = 0) Example: HKID card P ($) D (vertical) 0 Q

Factors affecting price elasticity of demand l. Substitutes l. Quantity l. More substitutes Easier to be replaced Price elasticity l. E. g. §When MTR started operation Ed of bus service (MTR South Island Line) §When 3 DTV launched Ed of TV sets §Technology of recycled energy Ed of traditional energy sources

Factors affecting price elasticity of demand l. Substitutes l. Substitutability l. Similar goods have high substitutability l. Higher substitutability Price elasticity l. E. g. §Snacks and soft drinks: Many brands Ed §Laptop (similar function): Many brands Ed §Bank services: Many banks in the market Ed §MTR service: Less choice Ed §University programmes: A few choice only Ed

Factors affecting price elasticity of demand l. What one has higher price elasticity of demand, hamburger or water? Why? l. Hamburger is more elastic las a kind of food more substitutes Ed las a brand many other brands Ed l. Water las is not elastic a kind of element (functional): no close substitutes Ed las a brand comparatively less brands Ed is not high

Factors affecting price elasticity of demand l. The 1. l l 2. l l l way of determining a good Salt As an element (Na. Cl) : No close substitute Very inelastic As different brands, e. g. Taikoo Salt, First choice, No frills: Many brands Very elastic Water As an element(H 2 O) : No close substitute Very inelastic As different brands, e. g. Watsons, Bonaqua, Vita Many brands Very elastic As different packages, e. g. 500 m. L, 1 L, 2 L, 5 L, 10 L, 1 Lx 6 Many packages Very elastic

Factors affecting price elasticity of demand l. Types l. Necessities l. Lower price elasticity, Price Less change in Qd l. E. g. electricity, tap water, public transports l. Luxuries l. Higher price elasticity, Price Greater response in Qd l. E. g. visiting Disneyland, travelling overseas l. Think about: l. Go to school l. Dating l. Wedding § banquet Fish fin

Factors affecting price elasticity of demand l. Time l. Longer time after ∆P l. Easier to find substitutes Ed Less change in Qd l. E. g. 1. Price of oil People take time to develop new technology More substitutes Less relying on oil Ed 2. Price of washing powder Shortly, no close substitutes Low Ed People take time to develop new technology: washing ball No need to use washing powder Ed of washing powder

Factors affecting price elasticity of demand l. Exceptional l. Case cases of Cross-Harbour Tunnel (1984, Dr. T. D. Hau) l. Toll Usage 15% , shift to vehicle ferry Inconvenient, and no way to find substitutes Go back to 98% of normal usage before P l. Case of Cross-Harbour Tunnel (Now) l. Toll Usage , shift to Eastern and Western Harbour Tunnels Time cost (Inconvenient) + higher tolls (EHT & WHT) Go back to similar usage before P

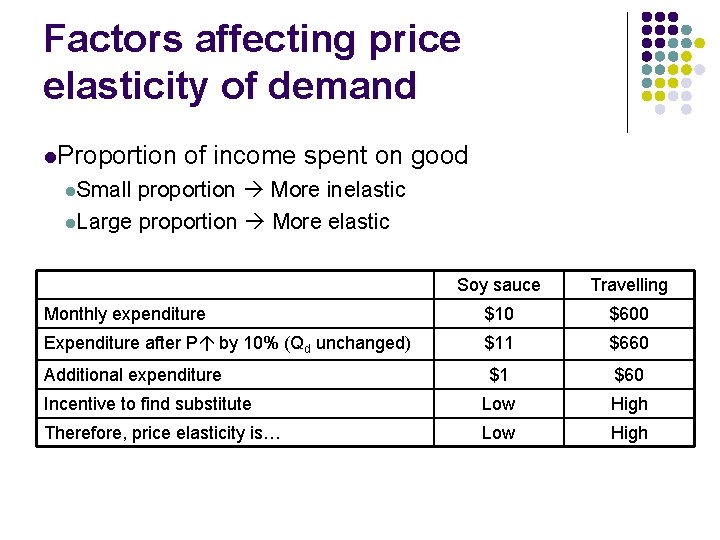
Factors affecting price elasticity of demand l. Proportion of income spent on good l. Small proportion More inelastic l. Large proportion More elastic Soy sauce Travelling Monthly expenditure $10 $600 Expenditure after P by 10% (Qd unchanged) $11 $660 Additional expenditure $1 $60 Incentive to find substitute Low High Therefore, price elasticity is… Low High

Factors affecting price elasticity of demand l Question (p. 84) Suppose the cost of finding substitutes for soy sauce and bus service are both $5. Explain whether you would find substitute for them. Answer: The benefit of finding substitutes for soy sauce is low relative to the cost. Therefore, consumers may not find substitutes for it. However, for bus service, the benefit is relatively high when compared to the cost, consumers may search for its substitutes.

Relationship between Ed and total revenue l l Total revenue (R) = Total expenditure = Total market value = Price x Quantity transacted =Px. Q E. g. PA = $10 per unit, Q = 50 units Total revenue of Good A = $10 x 50 = $500

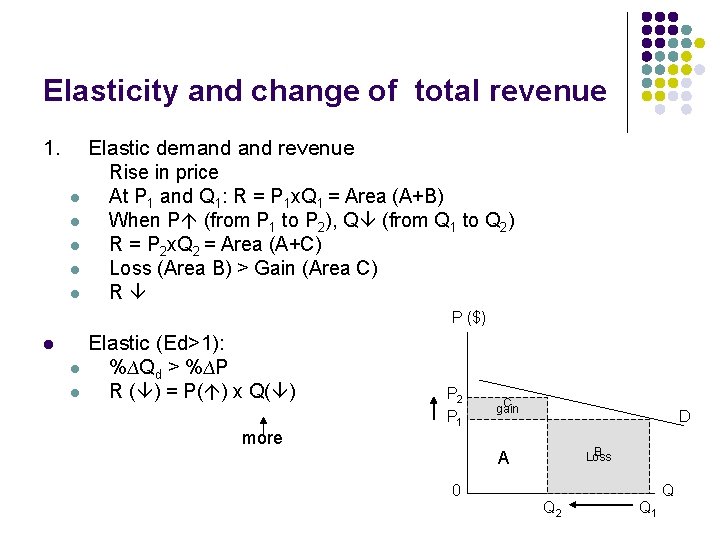
Elasticity and change of total revenue 1. l l l Elastic demand revenue Rise in price At P 1 and Q 1: R = P 1 x. Q 1 = Area (A+B) When P (from P 1 to P 2), Q (from Q 1 to Q 2) R = P 2 x. Q 2 = Area (A+C) Loss (Area B) > Gain (Area C) R P ($) l l l Elastic (Ed>1): %∆Qd > %∆P R ( ) = P( ) x Q( ) more P 2 P 1 C gain D B Loss A 0 Q 2 Q 1 Q

Elasticity and change of total revenue 1. l l l Elastic demand revenue Fall in price At P 1 and Q 1: R = P 1 x. Q 1 = Area (A+C) When P (from P 1 to P 2), Q (from Q 1 to Q 2) R = P 2 x. Q 2 = Area (A+B) Gain (Area B) > Loss (Area C) R P ($) l l l Elastic (Ed>1): %∆Qd > %∆P R ( ) = P ( ) x Q( ) more P 1 P 2 C Loss D B Gain A 0 Q 1 Q 2 Q

Elasticity and change of total revenue 2. l l l Inelastic demand revenue Rise in price At P 1 and Q 1: R = P 1 x. Q 1 = Area (A+B) When P (from P 1 to P 2), Q (from Q 1 to Q 2) R = P 2 x Q 2 = Area (A+C) Loss (Area B) < Gain (Area C) R P ($) l l l Elastic (Ed<1): %∆Qd < %∆P R ( ) = P( ) x Q( ) more P 2 C gain P 1 A 0 B Loss D Q 2 Q 1 Q

Elasticity and change of total revenue 2. l l l Inelastic demand revenue Fall in price At P 1 and Q 1: R = P 1 x. Q 1 = Area (A+C) When P (from P 1 to P 2), Q (from Q 1 to Q 2) R = P 2 x Q 2 = Area (A+B) Gain (Area B) < Loss (Area C) R P ($) l l l Elastic (Ed<1): %∆Qd < %∆P R ( ) = P ( ) x Q( ) more P 1 C Loss P 2 A 0 B Gain D Q 1 Q 2 Q

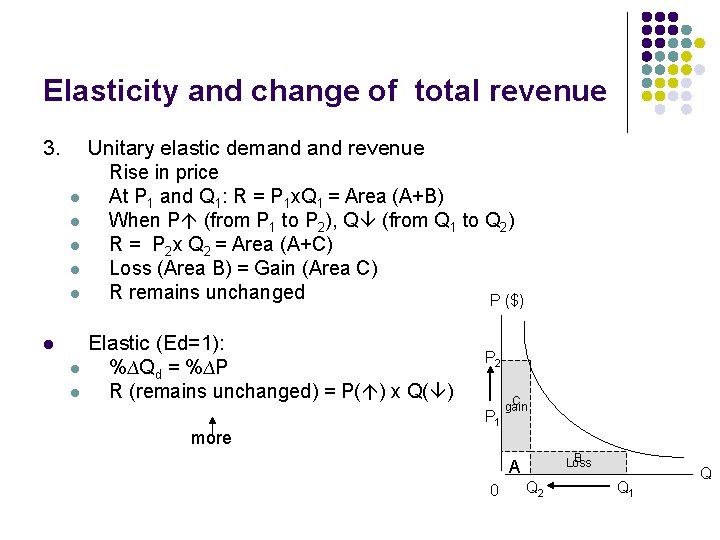
Elasticity and change of total revenue 3. l l l l Unitary elastic demand revenue Rise in price At P 1 and Q 1: R = P 1 x. Q 1 = Area (A+B) When P (from P 1 to P 2), Q (from Q 1 to Q 2) R = P 2 x Q 2 = Area (A+C) Loss (Area B) = Gain (Area C) R remains unchanged P ($) Elastic (Ed=1): %∆Qd = %∆P R (remains unchanged) = P( ) x Q( ) more P 2 P 1 C gain B Loss A 0 Q 2 Q 1 Q

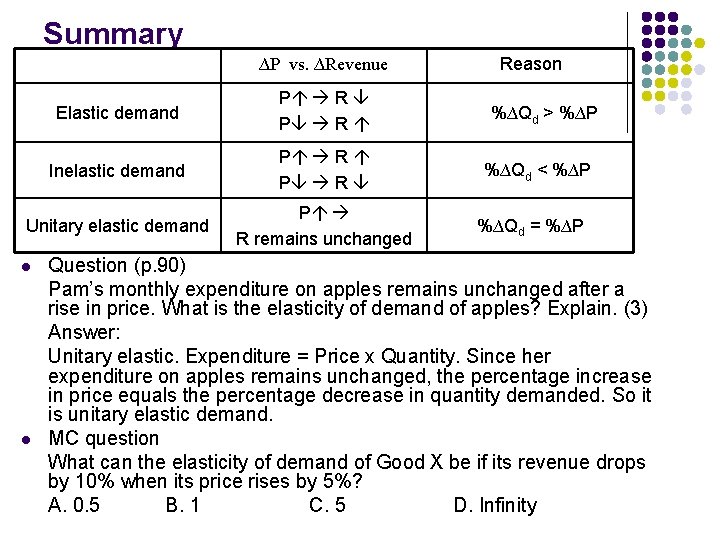
Summary ∆P vs. ∆Revenue Elastic demand P R Inelastic demand P R Unitary elastic demand P R remains unchanged l l Reason %∆Qd > %∆P %∆Qd < %∆P %∆Qd = %∆P Question (p. 90) Pam’s monthly expenditure on apples remains unchanged after a rise in price. What is the elasticity of demand of apples? Explain. (3) Answer: Unitary elastic. Expenditure = Price x Quantity. Since her expenditure on apples remains unchanged, the percentage increase in price equals the percentage decrease in quantity demanded. So it is unitary elastic demand. MC question What can the elasticity of demand of Good X be if its revenue drops by 10% when its price rises by 5%? A. 0. 5 B. 1 C. 5 D. Infinity

Effects on change in supply Supply curve shifts 1. Increase in supply P & Q a. b. c. Elastic demand (Ed>1): P R Unitary elastic demand (Ed=1): P R unchanged Inelastic demand (Ed<1): P R S 1 P ($) P 1 P 2 S 2 C Loss D B Gain A 0 Q 1 Q 2 Q

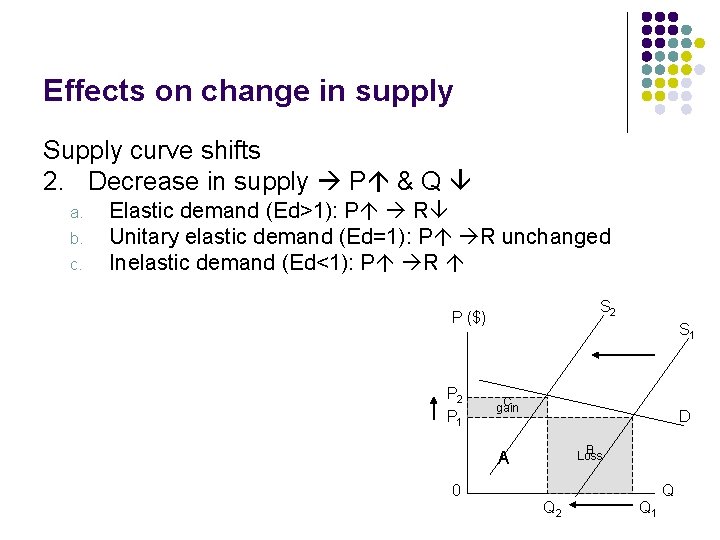
Effects on change in supply Supply curve shifts 2. Decrease in supply P & Q a. b. c. Elastic demand (Ed>1): P R Unitary elastic demand (Ed=1): P R unchanged Inelastic demand (Ed<1): P R S 2 P ($) P 2 P 1 S 1 C gain D B Loss A 0 Q 2 Q 1 Q

Effects on change in demand Demand curve shifts 3. Increase in demand P & Q a. Elastic demand (Ed>1): R b. Unitary elastic demand (Ed=1): R d c. Inelastic demand (Ed<1): R 4. Decrease in demand P & Q a. Elastic demand (Ed>1): R b. Unitary elastic demand (Ed=1): R c. Inelastic demand (Ed<1): R P ($) S P 2 P 1 D 2 D 1 C gain 0 Q 1 Q 2 Q

Price elasticity of supply l l l Measures the responsiveness of quantity supplied to a change in price Percentage change in quantity supplied over one percent change in price % ∆ QS Ed = -----%∆ P

Price elasticity of supply l l Example (p. 95) Midpoint formula

Price elasticity of supply l l Example (p. 95) Midpoint formula

Price elasticity of supply l l Example (p. 95) Taking the case of P

Price elasticity of supply l l Example (p. 95) Midpoint formula

5 Types of elasticity of supply P ($) l Elastic supply l l S Elasticity is greater than 1 (Es > 1) %∆ Qs > %∆P Q 0 l Inelastic supply l l P ($) Elasticity is smaller than 1 (Es < 1) %∆ Qs < %∆P S 0 Q

5 Types of elasticity of supply l Unitary elastic supply l l Elasticity equals 1 (Ed = 1) %∆ Qs = %∆P P ($) 0 S Q

5 Types of elasticity of supply l Perfectly elastic supply l l Elasticity equals infinity (Ed = ∞) A slightly rise in price will cause quantity supplied fall to 0. i. e. %∆P P ($) S (horizontal) 0 Q

5 Types of elasticity of supply l Perfectly inelastic supply l l Elasticity equals 0 (Ed = 0) Price change has no effect on the quantity supplied. (i. e. %∆Qs = 0) P ($) S (vertical) 0 Q

Factors affecting price elasticity of supply 1. Factors of production a. Values of factors of production different uses l. Products required non-specialized factors Price elasticity l. E. g. § Garment §P Qs no need to hire many factors non-specialized factors (e. g. low-skilled workers) leave the product and go to another industry Greater fall in Qs l. Products § Medical required specialized factors Price elasticity service (factor: equipment) P temporary, no increase in equipment because too specialized Qs has less effect on price change Or Demand P Existing equipment can’t be used for other purposes Change of Qs has less response

Factors affecting price elasticity of supply 1. Factors of production b. Adjustment cost of the cost of production l. Production §E. g. with non-specialized factors Es Clerk, easier to hire when needed l. Production §University with specialized factors Es principal, need to go through many procedures

Factors affecting price elasticity of supply Factors of production 1. Availability of information c. l More information Es Reserve capacity of equipment d. l More reserve Es Idle resources in the economy e. l More resources Es Occupational/Geographical Mobility f. l Higher mobility Es

Factors affecting price elasticity of supply Nature of products 2. Easily perishable Es l l 3. E. g. flowers at flower market: worthless if unsold Market structure and entry barrier l Restriction on output Es How to restrict? l l Entry barrier (e. g. registration is needed to become a doctor) Monopoly (e. g. water supply) Quota on imported goods

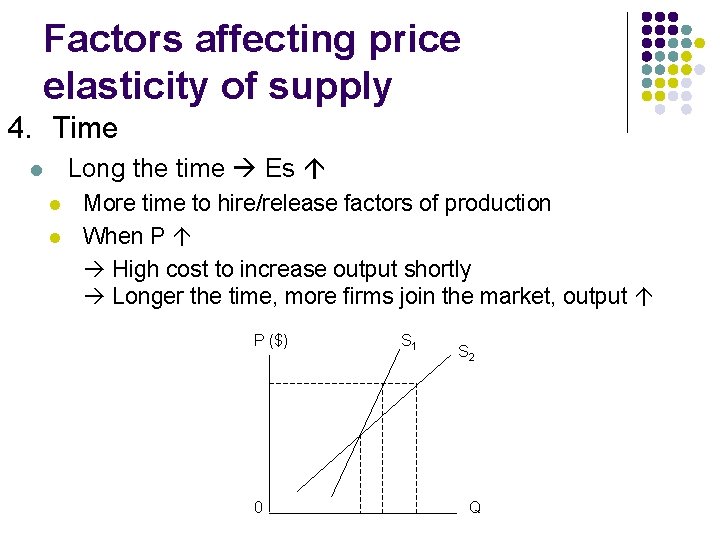
Factors affecting price elasticity of supply 4. Time Long the time Es l l l More time to hire/release factors of production When P High cost to increase output shortly Longer the time, more firms join the market, output P ($) 0 S 1 S 2 Q

Cases of perfectly inelastic supply 1. Output limitation Qs cannot be increases shortly l E. g. l § § § Cross Harbour Tunnel at peak hours Public Hospital (esp. maternity services) in HK Application of China Visa 0 Q

Cases of perfectly inelastic supply Output limitation 1. l l Qs cannot be increases shortly E. g. § § § Cross Harbour Tunnel at peak hours Public Hospital (esp. maternity services) in HK Application of China Visa Goods or services of non-profit making bodies 2. l l Qs cannot be changed in accordance to price change E. g. § § § Public housing (gov’t policy) Police service Social welfare service by NGO

Cases of perfectly inelastic supply 3. Government control Quotas l E. g. l § § Taxi license Broadcasting license 4. Land supply l l Qs is fixed In terms of natural resources, but not the ownership of a piece of land by the gov’t